This document provides an overview of a basic professional training course on nuclear physics and reactor theory. It covers topics like atomic structure, the structure of the atom including electrons and the nucleus, isotopes, radioactive decay, and nuclear reactions. The document is divided into several modules, with learning objectives provided for each section. It includes diagrams and examples to illustrate key concepts in nuclear physics.


























![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Energy levels in nuclei
• Nucleons can occupy different energy levels
− All nucleons in lowest possible energy levels: ground state
− Nucleons in higher energy levels: excited state
27
ground
state
energy
[MeV]
a) b)
0
etc.
etc.
0 0
10
20](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-27-320.jpg)
![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Binding energy of a nucleon
• Average energy needed to release one nucleon from the nucleus
28
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
0 20 40 60 80 100 120 140 160 180 200 220 240
binding
energy
per
nucleon
w
B
[MeV]
mass number A](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-28-320.jpg)

































































































![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Dependence of reactor period on reactivity
• the graph shows absolute
values of reactivity and reactor
period
• the shortest negative period
is -80 s.
− reactor can not shut down
faster than the decay of most
long-lived precursors
126
0.001
0.01 .02 .03 .04 .06.08 .1 .2 .3 .4 .6 .8 1.0 2.0
reactivity [$]
stable
period
[s]
0.01
0.1
1
10
100
10000
80
1000
positive reactivity
positive period
negative reactivity
negative period](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-126-320.jpg)













![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
135Xe during reactor start-up
• After reactor start-up, 135Xe concentration starts to grow
• Equilibrium concentration of 135Xe approx. 40 - 50 h after start-up
− equilibrium conc. depends on reactor power, but dependence not linear
140
25%
0
0
-500
-1000
-1500
-2000
-2500
-3000
time [hours]
reactivity
due
to
Xe
[pcm]
10 20 30 40 50 60 70 80 90 100
50%
75%
100%](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-140-320.jpg)

![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Reactivity due to 135Xe after shutdown
142
25%
0
0
500
1000
1500
2000
2500
3000
-500
-1000
-1500
-2000
-2500
-3000
time [hours]
reactivity
due
to
Xe
[pcm]
10 20 30 40 50 60 70 80 90 100
50%
75%
100%](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-142-320.jpg)






![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Critical boron concentration
• The critical boron concentration (CB) is defined as the concentration
of boron required for the reactor to be critical on full power with the
control rods withdrawn.
• Typical course of critical boron concentration over the fuel cycle:
149
4000
1000
2000
C
[ppm]
B
burn-up [MWd/MTU]
8000 12000 16000 20000](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-149-320.jpg)





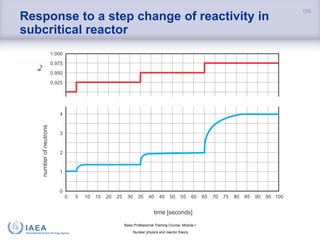




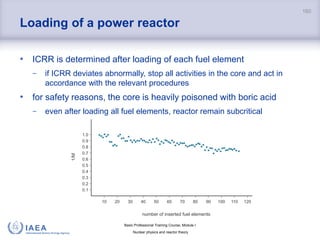

![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Definition of basic quantities
Heat flux is defined as the quantity of heat per unit time:
𝑄 =
∆𝑄
∆𝑡
[J/s = W]
Heat flux density is heat flux per unit surface area [W/m2].
162
Heat is energy which passes from a point of higher temperature to
a point of lower temperature.
If there is no difference in temperature, there can be no heat transfer.](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-162-320.jpg)


![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Heat conduction equation
𝑄 =
𝜆 𝐴 Δ𝑇
Δ𝑥
heat conductivity [W/mK]
A surface area of the wall [m2]
T temperature difference [K]
x wall thickness [m]
165](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-165-320.jpg)
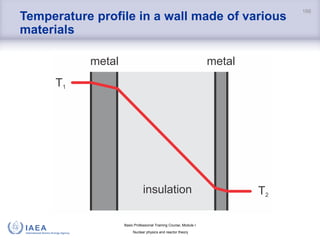




![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Equation of heat transfer
𝑄 = ℎc 𝐴 Δ𝑇
hc heat transfer coefficient [W/m2K]
A wall surface area [m2]
T temperature difference between wall and fluid [K]
• hc depends on fluid velocity, pressure, temperature, the flow
regimes of potential two-phase flow, etc. It is determined
experimentally.
171](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-171-320.jpg)







![Basic Professional Training Course; Module I
Nuclear physics and reactor theory
Average linear power density
• thermal power released per unit fuel rod length [kW/m]
Example:
− thermal power of a PWR: 1994 MW
− number of fuel elements in the core: 121
− number of fuel rods in each element: 235
− length of fuel rod: 3.6 m
− fraction of heat released in the fuel: 97.4%
𝑞 =
1994 ∙ 1000 kW ∙ 0.974
121 ∙ 235 ∙ 3.6 m
= 18.7 kW/m
• Linear power density is not equal for all the rods in a fuel element
− varies among individual elements
− varies with the height of a fuel rod in the core
179](https://image.slidesharecdn.com/module01nuclearphysicsandreactortheory-210914170036/85/Module01-nuclear-physics-and-reactor-theory-179-320.jpg)



