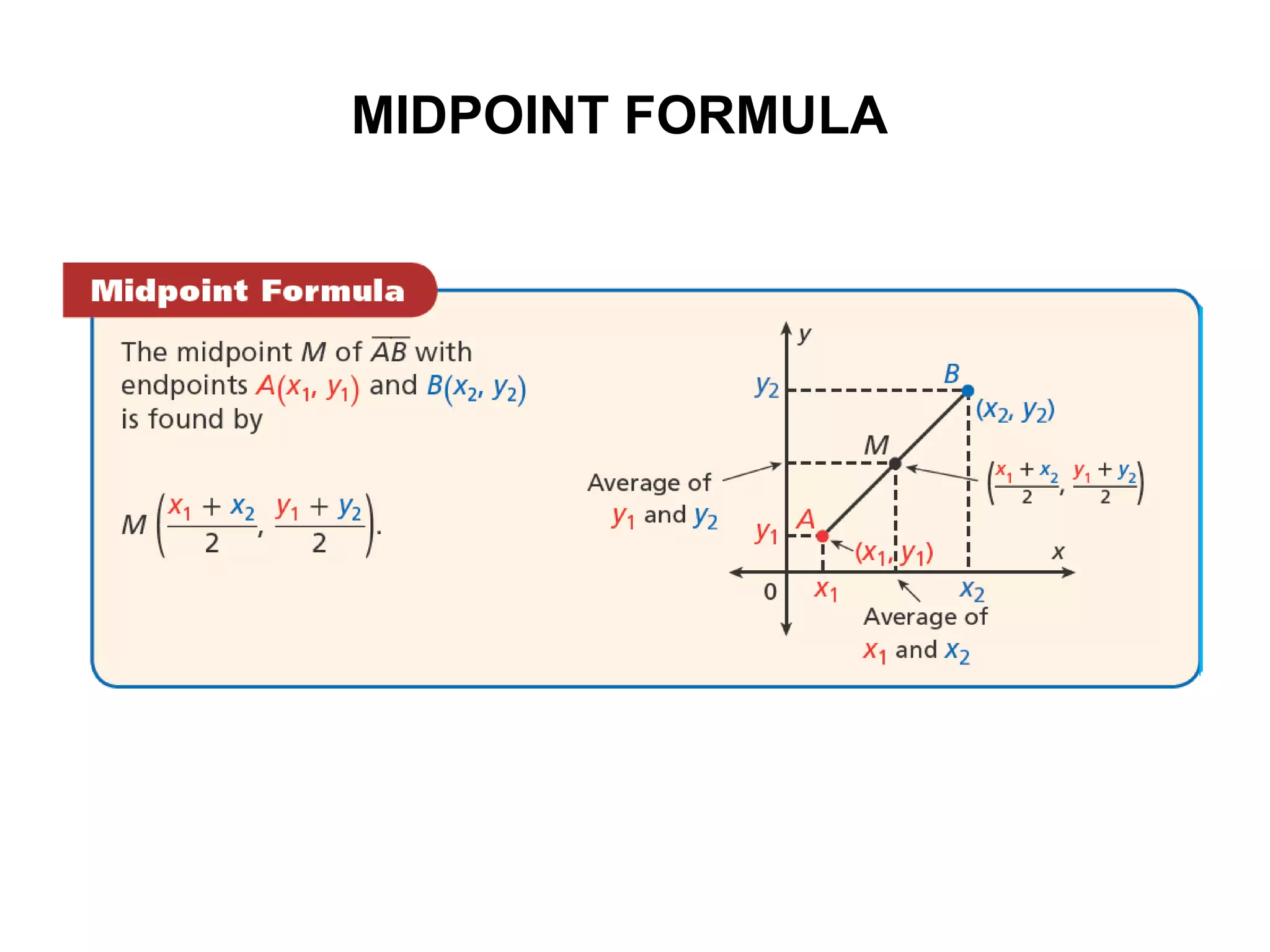
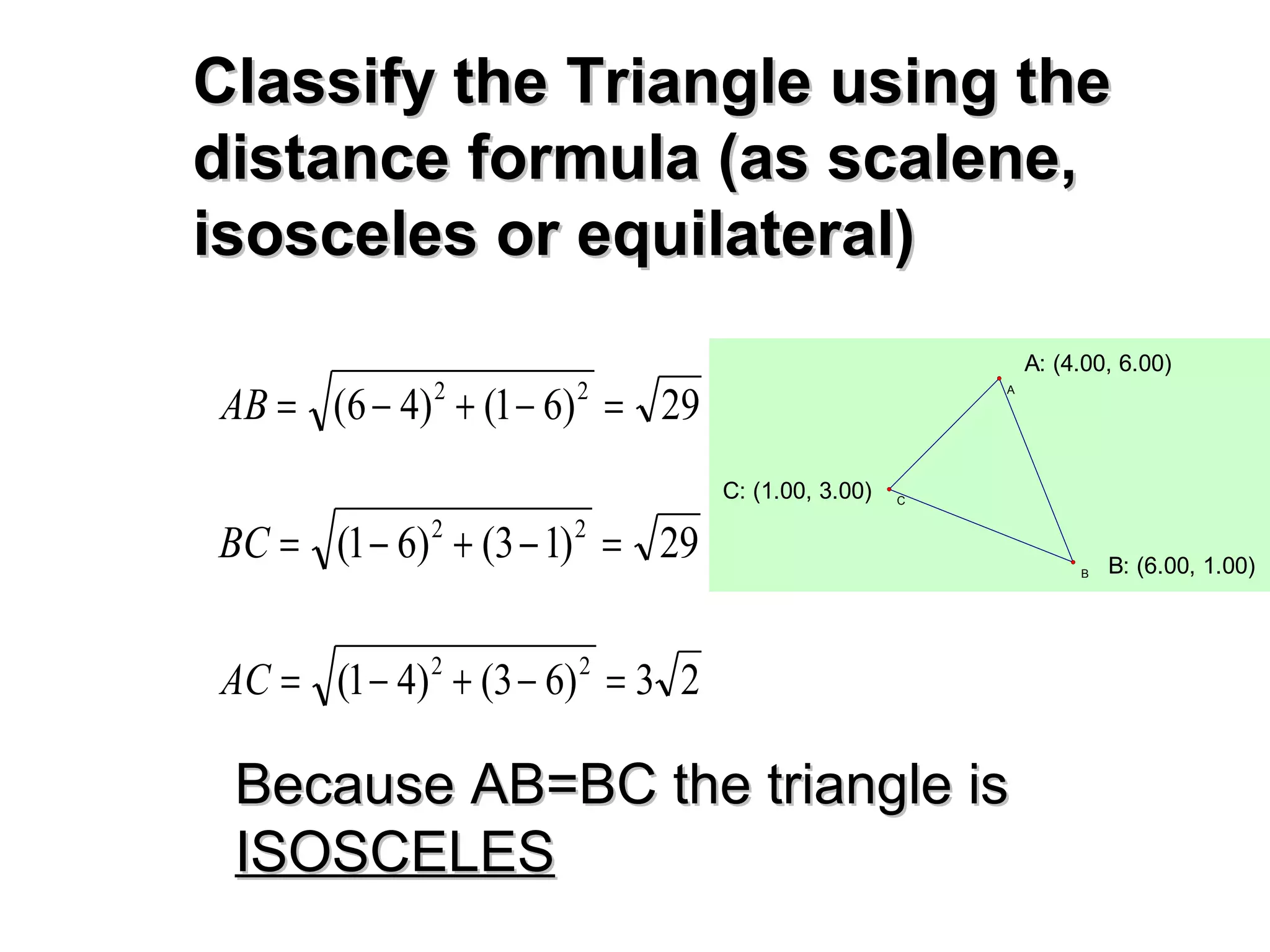
1. The document discusses the distance and midpoint formulas in coordinate geometry. 2. It provides the formulas for finding the distance between two points and the midpoint of a line segment. 3. Examples are given of using the formulas to find distances and midpoints, as well as classifying triangles and finding endpoint coordinates given a midpoint.

1. 10.1 The Distance
and Midpoint
Formulas
Algebra 2
Mr. Swartz

2. Objectives/Standard/Assignment
Objectives:
1. Find the distance between two points
in the coordinate plane, and
2. Find the midpoint of a line segment in
the coordinate plane.

3. Geometry Review!
• What is the differenceWhat is the difference
between the symbols AB andbetween the symbols AB and
AB?AB?
Segment ABSegment AB
TheThe lengthlength ofof
Segment ABSegment AB

4. The Distance Formula
• The Distance d
between the points
(x1,y1) and (x2,y2) is :
2
12
2
12 )()( yyxxd −+−=

5. The Pythagorean Theorem states that if a right triangle has legs
of lengths a and b and a hypotenuse of length c, then a2
+ b2
= c2
.
Remember!

6. Find the distance between
the two points.
• (-2,5) and (3,-1)(-2,5) and (3,-1)
• Let (xLet (x11,y,y11) = (-2,5) and (x) = (-2,5) and (x22,y,y22) = (3,-1)) = (3,-1)
22
)51())2(3( −−+−−=d
3625+=d
81.761 ≈=d

7. Classify the Triangle using theClassify the Triangle using the
distance formula (as scalene,distance formula (as scalene,
isosceles or equilateral)isosceles or equilateral)
29)61()46( 22
=−+−=AB
29)13()61( 22
=−+−=BC
23)63()41( 22
=−+−=AC
Because AB=BC the triangle isBecause AB=BC the triangle is
ISOSCELESISOSCELES
C: (1.00, 3.00)
B: (6.00, 1.00)
A: (4.00, 6.00)
C
B
A

8. The Midpoint Formula
• The midpoint between the twoThe midpoint between the two
points (xpoints (x11,y,y11) and (x) and (x22,y,y22) is:) is:
)
2
,
2
( 1212 yyxx
m
++
=

9. MIDPOINT FORMULA

10. Find the midpoint of theFind the midpoint of the
segment whose endpointssegment whose endpoints
are (6,-2) & (2,-9)are (6,-2) & (2,-9)





 −+−+
2
92
,
2
26





 −
2
11
,4

11. Find the coordinates of the midpoint of GH
with endpoints G(–4, 3) and H(6, –2).
Substitute.
Write the
formula.
Simplify.
Additional Example 1: Finding the Coordinates of a Midpoint
G(–4, 3)
H(6, -2)

12. Additional Example 2:
Finding the Coordinates of an Endpoint
Step 1 Let the coordinates of P equal (x, y).
Step 2 Use the Midpoint Formula.
P is the midpoint of NQ. N has coordinates
(–5, 4), and P has coordinates (–1, 3). Find the
coordinates of Q.

13. Additional Example 2 Continued
Multiply both
sides by 2.
Isolate the
variables.
–2 = –5 + x
+5 +5
3 = x
6 = 4 + y
−4 −4
Simplify. 2 = y
Set the
coordinates equal.
Step 3 Find the x-
coordinate.
Find the
y-coordinate.
Simplify.