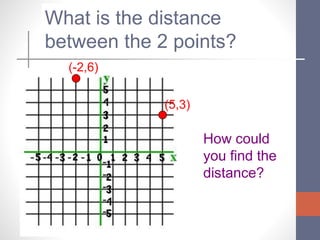
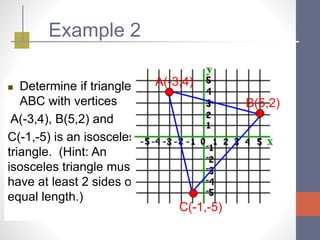
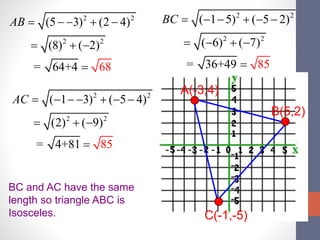
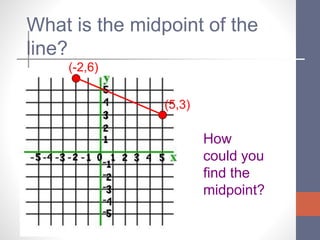
The document explains the distance and midpoint formulas for finding the distance between two points and the midpoint of a line segment between two points. It provides the formulas, sings them to familiar tunes for memorization, and includes examples of using the formulas to calculate distances and midpoints and find missing coordinates. It also shows how to find the equation of a line perpendicular to the midpoint of two points.

1. The Distance and
Midpoint Formula

2. What is the distance
between the 2 points?
(-2,6)
(5,3)
How could
you find the
distance?

3. The Distance Formula
 The distance
between any two
points with
coordinates (x1,y1) an
(x2,y2) is given by the
following formula:
2 2
2 1 2 1
( ) ( )
d x x y y
   
"The Distance Formula"
sung to the tune of "On Top of Old
Smokey"
When finding the distance
Between the two points,
Subtract the two x's
The same for the y's.
Now square these two numbers,
And find out their sum.
When you take the square root
Then you are all done!

4. Example 1
 Find the distance between the points with
coordinates (3,5) and (6,4).
2 2
2 1 2 1
( ) ( )
d x x y y
   
2 2
(6 3) (4 5)
d    
2 2
(3) ( 1)
d   
9 1
d  
10
d 
 3.16 units

5. Example 2
 Determine if triangle
ABC with vertices
A(-3,4), B(5,2) and
C(-1,-5) is an isosceles
triangle. (Hint: An
isosceles triangle must
have at least 2 sides of
equal length.)
A(-3,4)
B(5,2)
C(-1,-5)

6. 2 2
2 2
(5 3) (2 4)
(8) ( 2)
6
64+ 8
= 4
AB     
  

2 2
2 2
( 1 5) ( 5 2)
( 6) ( 7)
= 36+ 5
4 8
9
BC      
   

2 2
2 2
( 1 3) ( 5 4)
(2) ( 9)
= 4+ 5
8 8
1
AC       
  

A(-3,4)
B(5,2)
C(-1,-5)
BC and AC have the same
length so triangle ABC is
Isosceles.

7. What is the midpoint of the
line?
(-2,6)
(5,3)
How
could you
find the
midpoint?

8. The Midpoint Formula
 The coordinates of the
midpoint of a line
segment whose
endpoints are (x1, y1) and
(x2, y2) are given by the
following formula:
1 2 1 2
( , ) ,
2 2
x x y y
x y
 
 
  
 
"The Midpoint Formula"
sung to the tune of "The Itsy Bitsy
Spider"
When finding the midpoint of two
points on a graph,
Add the two x's and cut their sum
in half.
Add up the y's and divide 'em by a
two,
Now write 'em as an ordered pair
It’s the middle of the two.

9. Example 1
 Find the midpoint between the points
with coordinates (6,2) and (-3,-4).
6 3 2 4
( , ) ,
2 2
x y
 
 
  
 
( , ) (1.5, 1)
x y  
3 2
( , ) ,
2 2
x y

 
  
 
(1.5, 1)


10. Example 2
 If the coordinate (2, -3) is the
midpoint of line AB and the endpoint
A is (5, 4), what is the missing
coordinate B?
1 2
2
x x
x


5
2
2
x


4 5 x
 
1 x
 
1 2
2
y y
y


4
3
2
y

 
6 4 y
  
10 y
 
(-1, -10)

11. Example 3
 Find the equation of a line that is
perpendicular to the midpoint of a line
that contains the endpoints (4, 6) and (-
2, 4).
Slope of Line:
 Slope of Line:
Midpoint:
Equation of Line:
6 4 2
4 2 6
1
3
m

  

3
m
  
4 2 6 4
( , ) ,
2
(1,5)
2
x y
 
 
 
 
 
5 3( 1)
y x
   