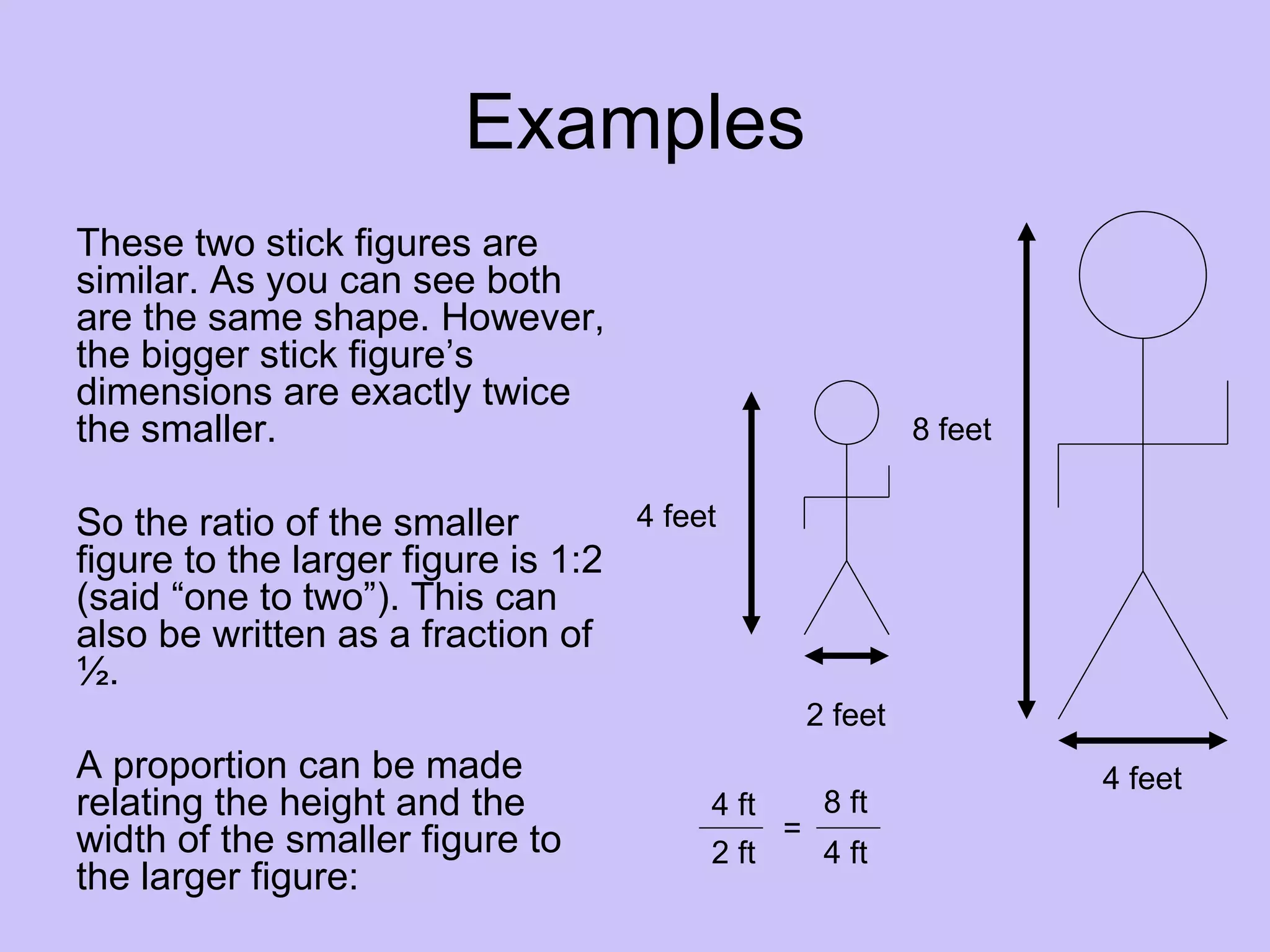
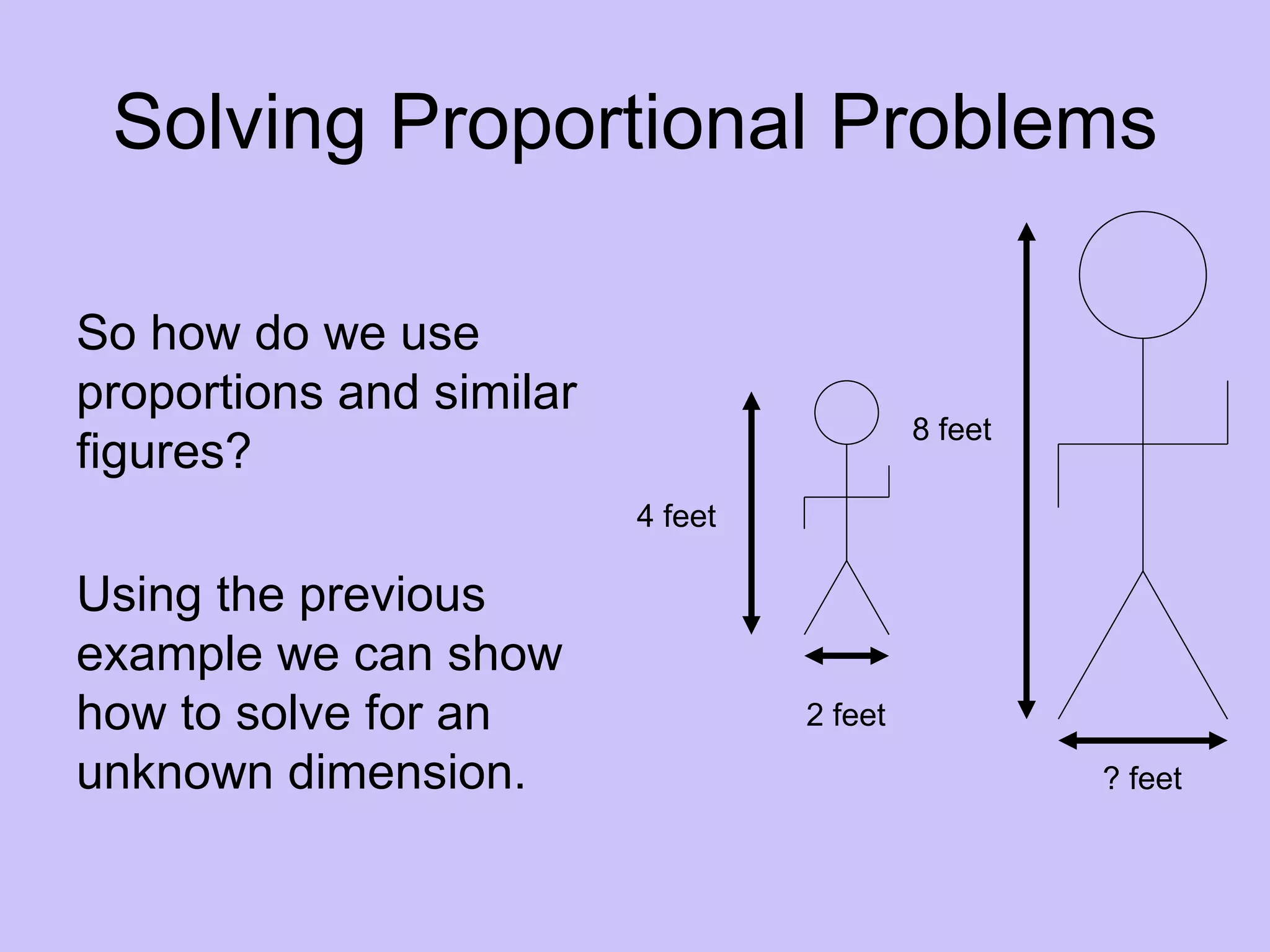
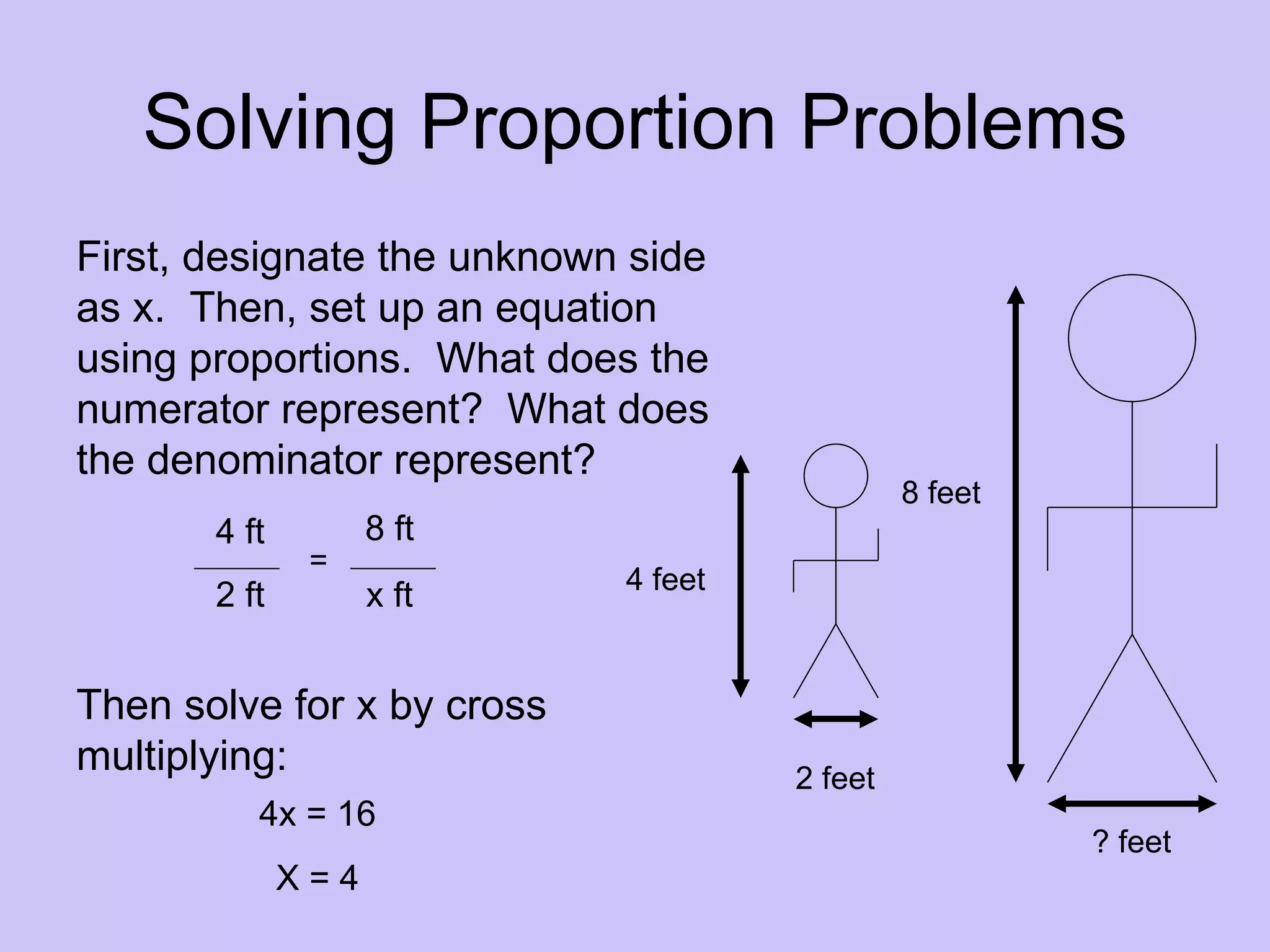
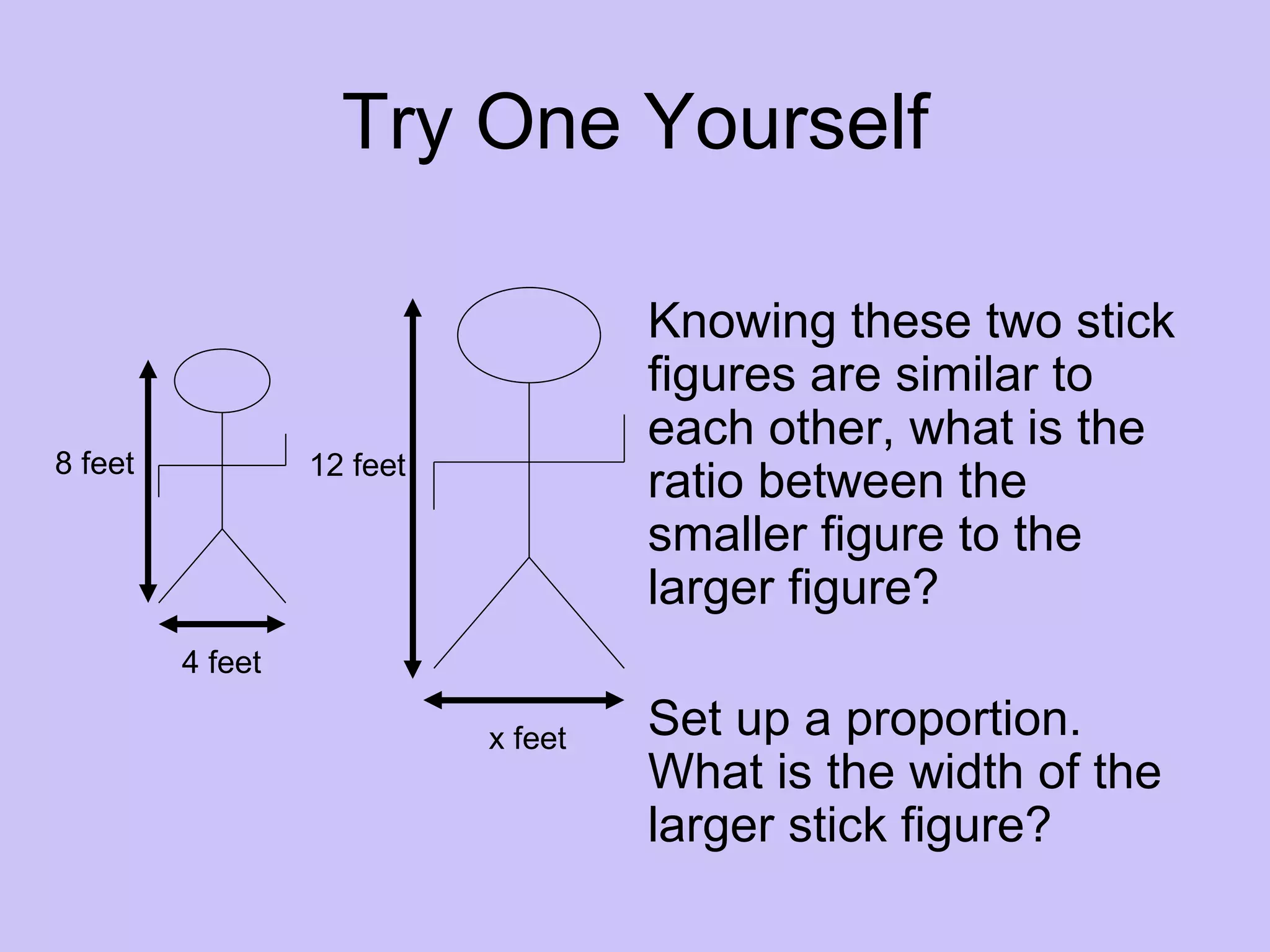
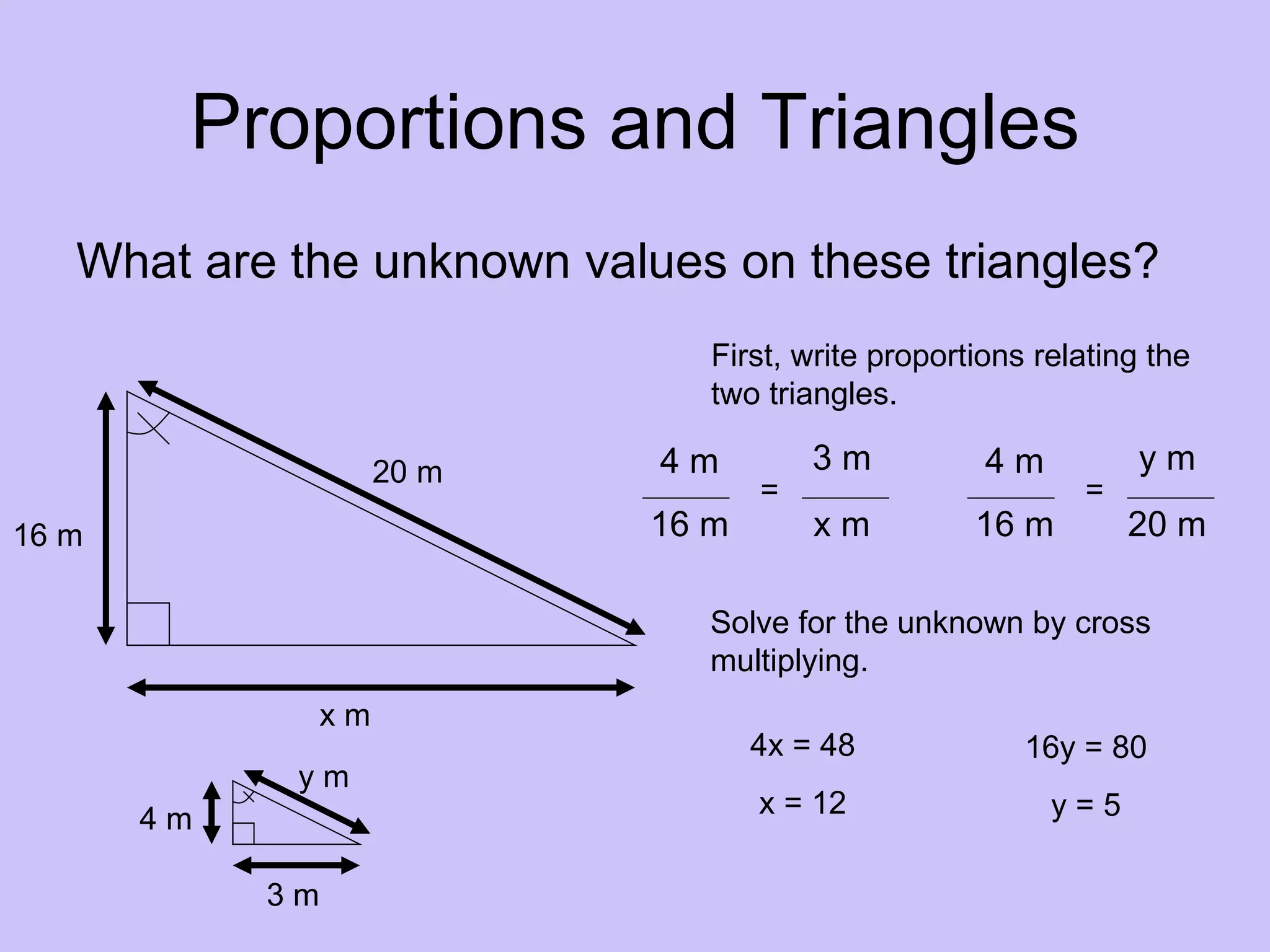
This document discusses proportions and similar figures in geometry. It explains that proportions involve equal ratios that can be used with similar figures, which have the same shape but different sizes. Examples show setting up and solving proportions to find unknown dimensions of similar figures. The document provides practice problems involving similar right triangles and real-world applications of using proportions to calculate heights. It discusses accuracy and potential sources of error when using this method.

1. Proportions

2. Proportions
What are proportions?
- If two ratios are equal, they form a proportion.
Proportions can be used in geometry when working with
similar figures. 1 4
= 1:3 = 3:9
2 8
What do we mean by similar?
- Similar describes things which have the same shape
but are not the same size.

3. Examples
These two stick figures are
similar. As you can see both
are the same shape. However,
the bigger stick figure’s
dimensions are exactly twice
the smaller. 8 feet
So the ratio of the smaller 4 feet
figure to the larger figure is 1:2
(said “one to two”). This can
also be written as a fraction of
½.
2 feet
A proportion can be made 4 feet
relating the height and the 4 ft 8 ft
width of the smaller figure to =
2 ft 4 ft
the larger figure:

4. Solving Proportional Problems
So how do we use
proportions and similar
8 feet
figures?
4 feet
Using the previous
example we can show
how to solve for an 2 feet
unknown dimension. ? feet

5. Solving Proportion Problems
First, designate the unknown side
as x. Then, set up an equation
using proportions. What does the
numerator represent? What does
the denominator represent?
8 feet
4 ft 8 ft
=
4 feet
2 ft x ft
Then solve for x by cross
multiplying: 2 feet
4x = 16
? feet
X=4

6. Try One Yourself
Knowing these two stick
figures are similar to
each other, what is the
8 feet 12 feet
ratio between the
smaller figure to the
larger figure?
4 feet
x feet Set up a proportion.
What is the width of the
larger stick figure?

7. Similar Shapes
In geometry similar shapes are very important.
This is because if we know the dimensions of one
shape and one of the dimensions of another shape
similar to it, we can figure out the unknown
dimensions.

8. Triangle and Angle Review
Today we will be working with
right triangles. Recall that one of
the angles in a right triangle
equals 90o. This angle is
represented by a square in the
corner.
90o angle
To designate equal angles we
will use the same symbol for both
angles. equal angles

9. Proportions and Triangles
What are the unknown values on these triangles?
First, write proportions relating the
two triangles.
20 m 4m 3m 4m ym
= =
16 m 16 m xm 16 m 20 m
Solve for the unknown by cross
multiplying.
xm
4x = 48 16y = 80
ym
x = 12 y=5
4m
3m

10. Triangles in the Real World
Do you know how tall your school building is?
There is an easy way to find out using right triangles.
To do this create two similar triangles
using the building, its shadow, a
smaller object with a known height
(like a yardstick), and its shadow.
The two shadows can be measured,
and you know the height of the yard
stick. So you can set up similar
triangles and solve for the height of
the building.

11. Solving for the Building’s Height
Here is a sample calculation for building
the height of a building:
x ft 48 ft x feet
=
3 ft 4 ft
48 feet
4x = 144
yardstick
x = 36 3 feet
The height of the building is 36 4 feet
feet.

12. Accuracy and Error
Do you think using proportions to calculate the
height of the building is better or worse than
actually measuring the height of the building?
Determine your height by the same technique
used to determine the height of the building. Now
measure your actual height and compare your
answers.
Were they the same? Why would there be a
difference?

13. Cool Proportions
• Measure wrist to fingertip. Measure top of
shoulder to wrist. Write the ratio of your
hand length to your arm length. What
whole number ratio is it close to?
• Measure fingertip to heart. Double this
length. Is this equal to your height?
• Measure your foot. Measure forearm (wrist
to elbow). What is the ratio of your foot to
your arm?

14. Similar Figure Activity
• On loose-leaf, record your proportions to
solve for x. You don’t need to draw the
figures over (just make sure to write the
number of the problem)
• How many can you finish in 15 min?

15. Similar Figure Word Problems
• On loose-leaf, write down key information
(not entire problem). Show proportion and
solve.
• Green paper- solve to nearest whole
number
• Pink paper- solve to nearest tenth