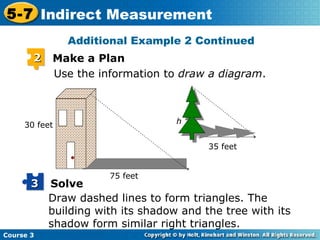
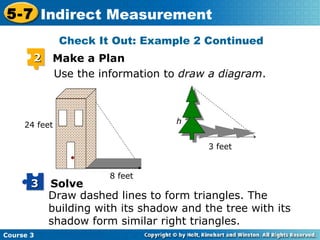
This document provides examples of using indirect measurement to solve for unknown distances. It begins with an example of using similar triangles to find the length of side EG of triangle EFG given the lengths of sides AB, AC, and EF of similar triangle ABC. It then gives another example using similar triangles formed by a building, its shadow, and a tree and its shadow to calculate the height of the tree. Finally, it provides two practice problems asking the reader to use indirect measurement to solve for the width of a river and the height of a tree.

1. Warm Up Lesson Presentation 5-7 Indirect Measurement Course 3

2. Warm Up Solve each proportion. 1. 2. 3. 4. x = 45 x = 20 x = 2 x = 4 x 75 3 5 = 2.4 8 6 x = x 6 9 27 = 8 7 x 3.5 =

3. Learn to find measures indirectly by applying the properties of similar figures.

4. Vocabulary indirect measurement

5. Sometimes, distances cannot be measured directly. One way to find such a distance is to use indirect measurement , a way of using similar figures and proportions to find a measure.

6. Additional Example 1: Geography Application Triangles ABC and EFG are similar. Triangles ABC and EFG are similar. Find the length of side EG . B A C 3 ft 4 ft F E G 9 ft x

7. Additional Example 1 Continued = Set up a proportion. Substitute 3 for AB, 4 for AC, and 9 for EF. 3 x = 36 Find the cross products. The length of side EG is 12 ft. x = 12 Triangles ABC and EFG are similar. Find the length of side EG. = = Divide both sides by 3. AB AC EF EG 3 4 9 x 3x 3 36 3

8. Check It Out: Example 1 Triangles DEF and GHI are similar. Triangles DEF and GHI are similar. Find the length of side HI . 2 in E D F 7 in H G I 8 in x

9. Check It Out: Example 1 Continued = Set up a proportion. Substitute 2 for DE, 7 for EF, and 8 for GH. 2 x = 56 Find the cross products. The length of side HI is 28 in. x = 28 = = Divide both sides by 2. Triangles DEF and GHI are similar. Find the length of side HI . DE EF GH HI 2 7 8 x 2x 2 56 2

10. A 30-ft building casts a shadow that is 75 ft long. A nearby tree casts a shadow that is 35 ft long. How tall is the tree? Additional Example 2: Problem Solving Application The answer is the height of the tree. List the important information: • The length of the building’s shadow is 75 ft. • The height of the building is 30 ft. • The length of the tree’s shadow is 35 ft. 1 Understand the Problem

11. Additional Example 2 Continued Use the information to draw a diagram . h Draw dashed lines to form triangles. The building with its shadow and the tree with its shadow form similar right triangles. 2 Make a Plan Solve 3 75 feet 30 feet 35 feet

12. 30 75 = h 35 Corresponding sides of similar figures are proportional. 75 h = 1050 Find the cross products. The height of the tree is 14 feet. h = 14 = Divide both sides by 75. Additional Example 2 Continued Solve 3 75h 75 1050 75

13. Since = 2.5, the building’s shadow is 2.5 times its height. So, the tree’s shadow should also be 2.5 times its height and 2.5 of 14 is 35 feet. Look Back 75 30 Additional Example 2 Continued 4

14. A 24-ft building casts a shadow that is 8 ft long. A nearby tree casts a shadow that is 3 ft long. How tall is the tree? Check It Out: Example 2 The answer is the height of the tree. List the important information: • The length of the building’s shadow is 8 ft. • The height of the building is 24 ft. • The length of the tree’s shadow is 3 ft. 1 Understand the Problem

15. Use the information to draw a diagram . h Draw dashed lines to form triangles. The building with its shadow and the tree with its shadow form similar right triangles. Check It Out: Example 2 Continued 2 Make a Plan Solve 3 3 feet 8 feet 24 feet

16. 24 8 = h 3 Corresponding sides of similar figures are proportional. 72 = 8 h Find the cross products. The height of the tree is 9 feet. 9 = h = Divide both sides by 8. Check It Out: Example 2 Continued Solve 3 72 8 8 h 8

17. Since = , the building’s shadow is times its height. So, the tree’s shadow should also be times its height and of 9 is 3 feet. Look Back 8 24 1 3 1 3 1 3 1 3 Check It Out: Example 2 Continued 4

18. 1. Vilma wants to know how wide the river near her house is. She drew a diagram and labeled it with her measurements. How wide is the river? 2. A yardstick casts a 2-ft shadow. At the same time, a tree casts a shadow that is 6 ft long. How tall is the tree? Lesson Quiz 7.98 m 9 ft w 7 m 5 m 5.7 m