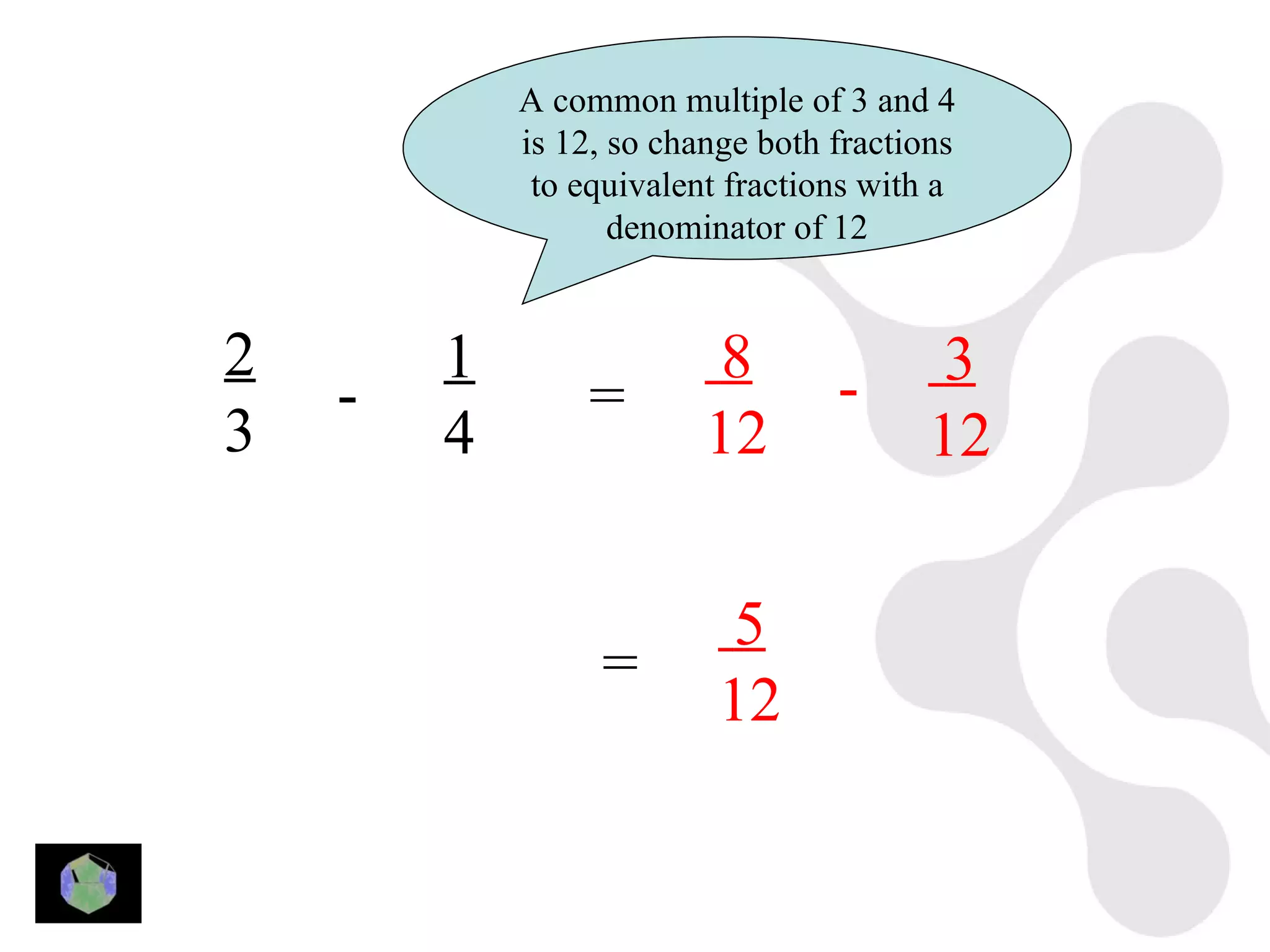
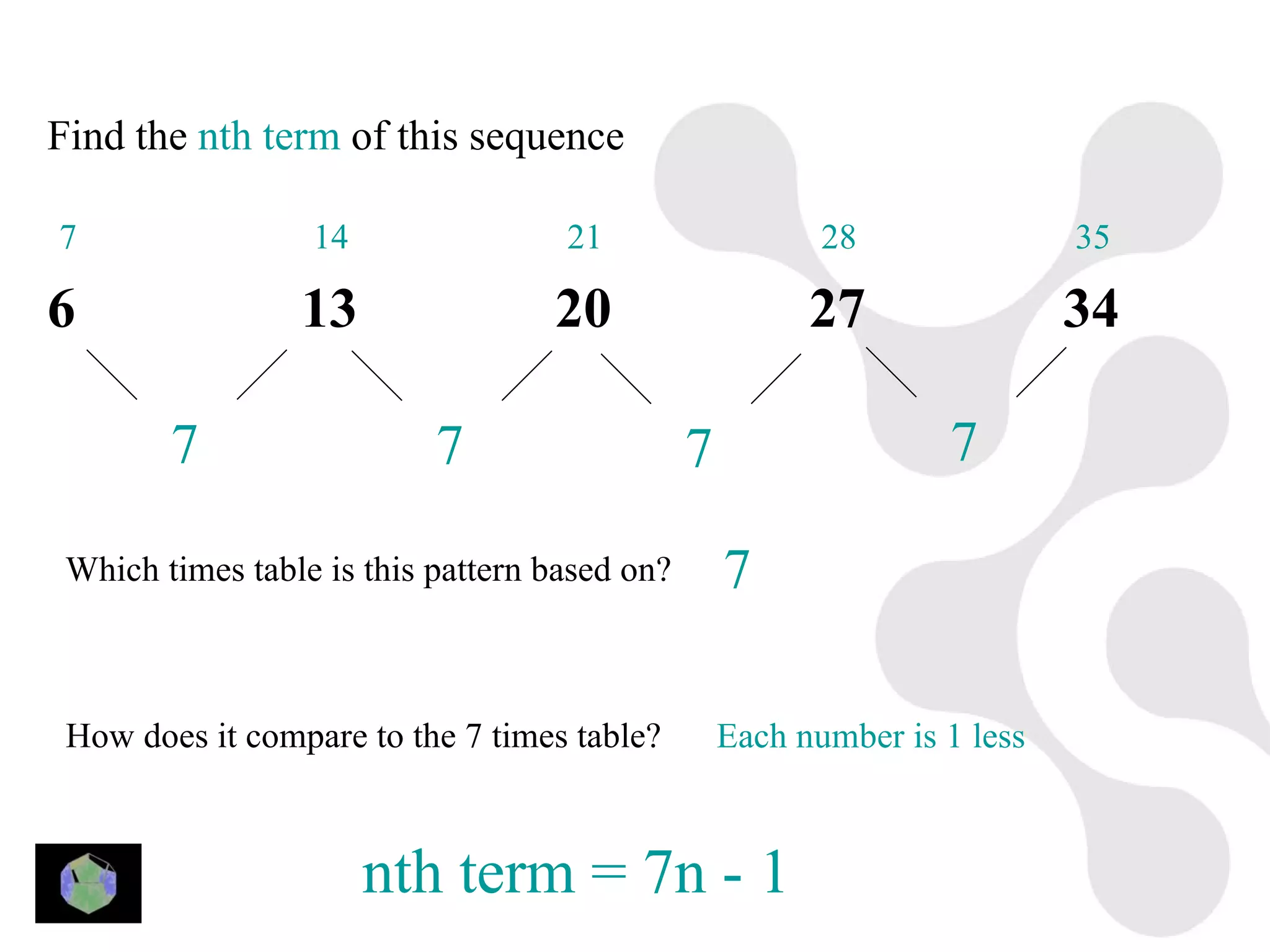
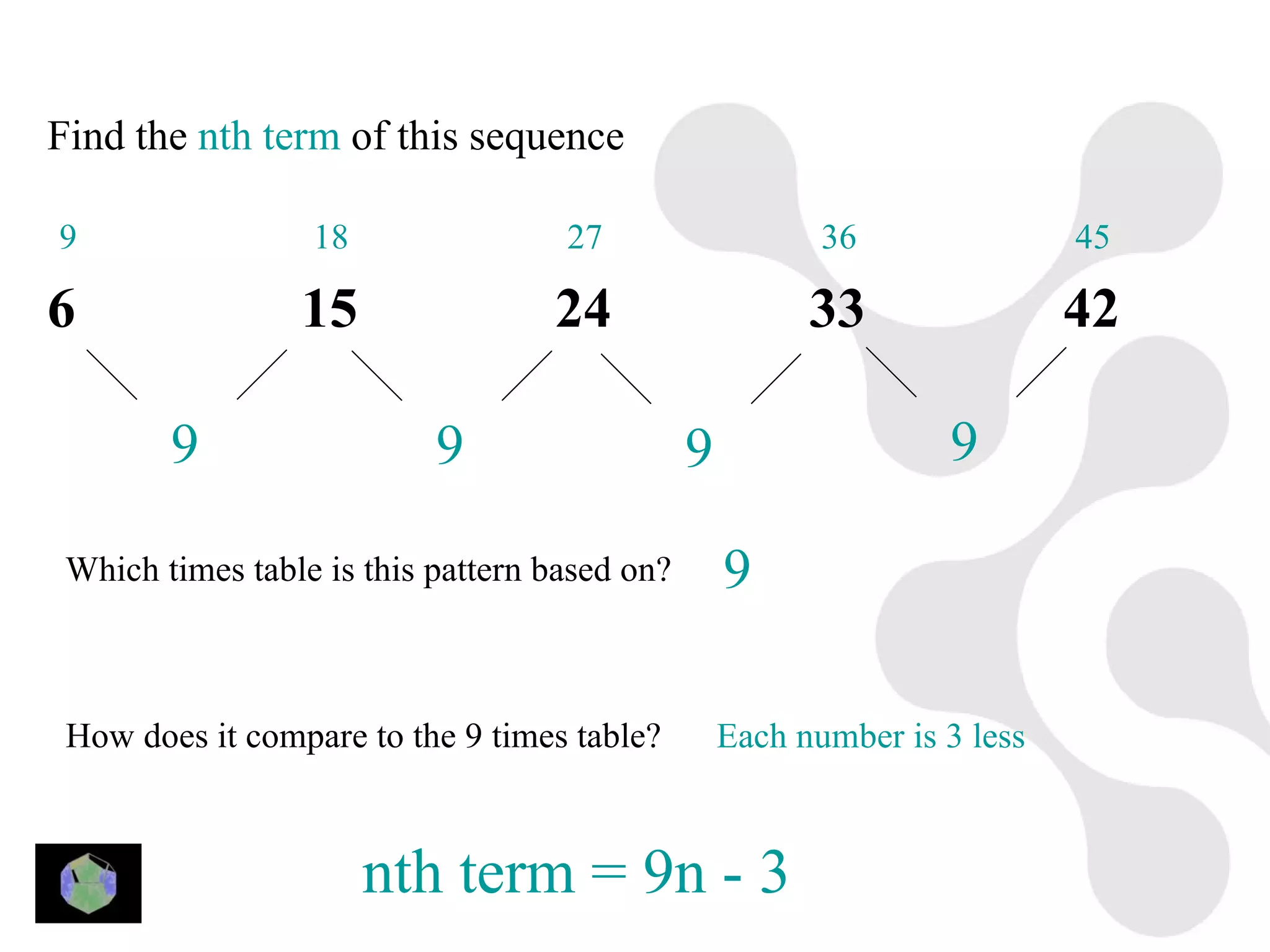
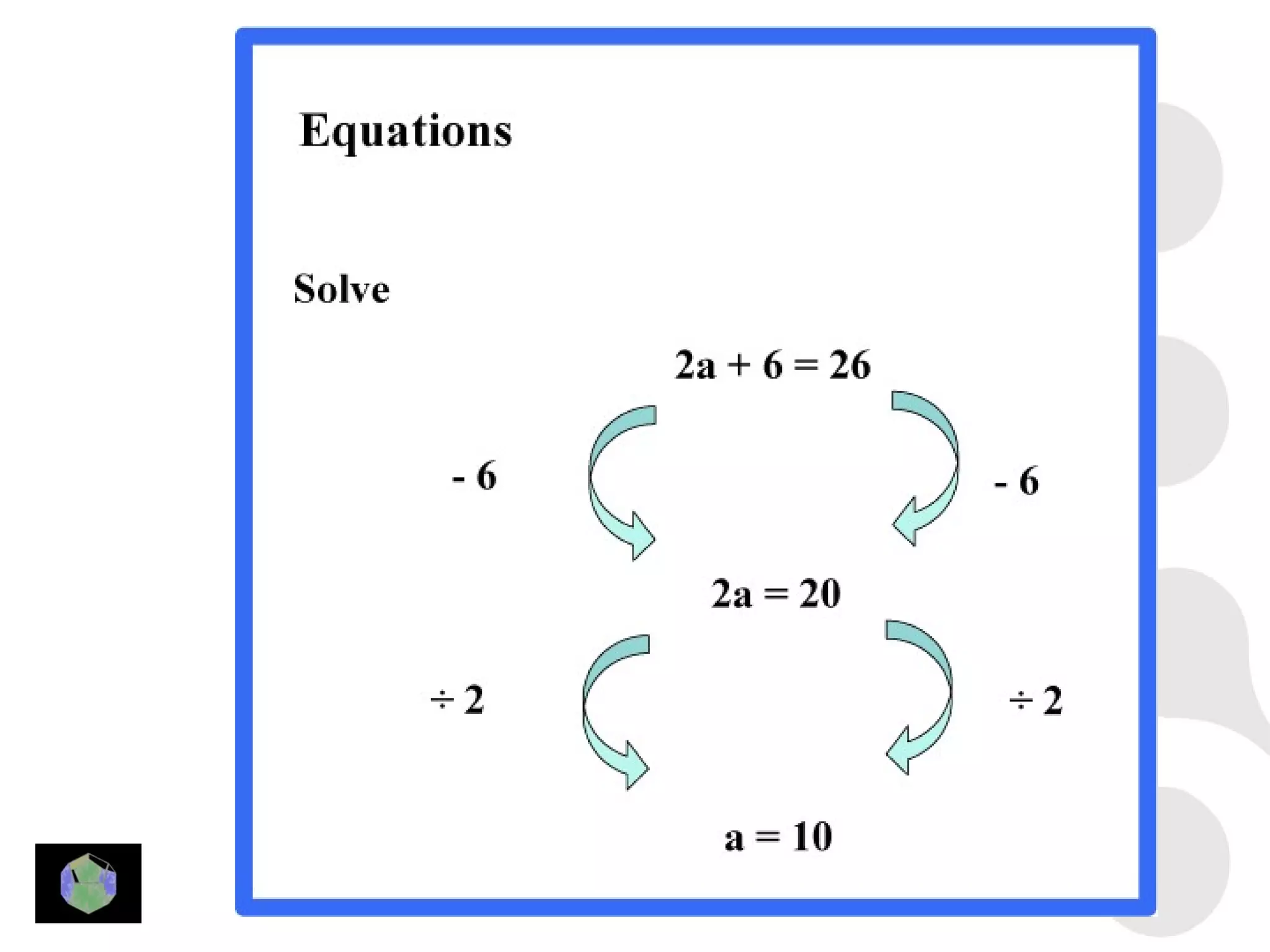
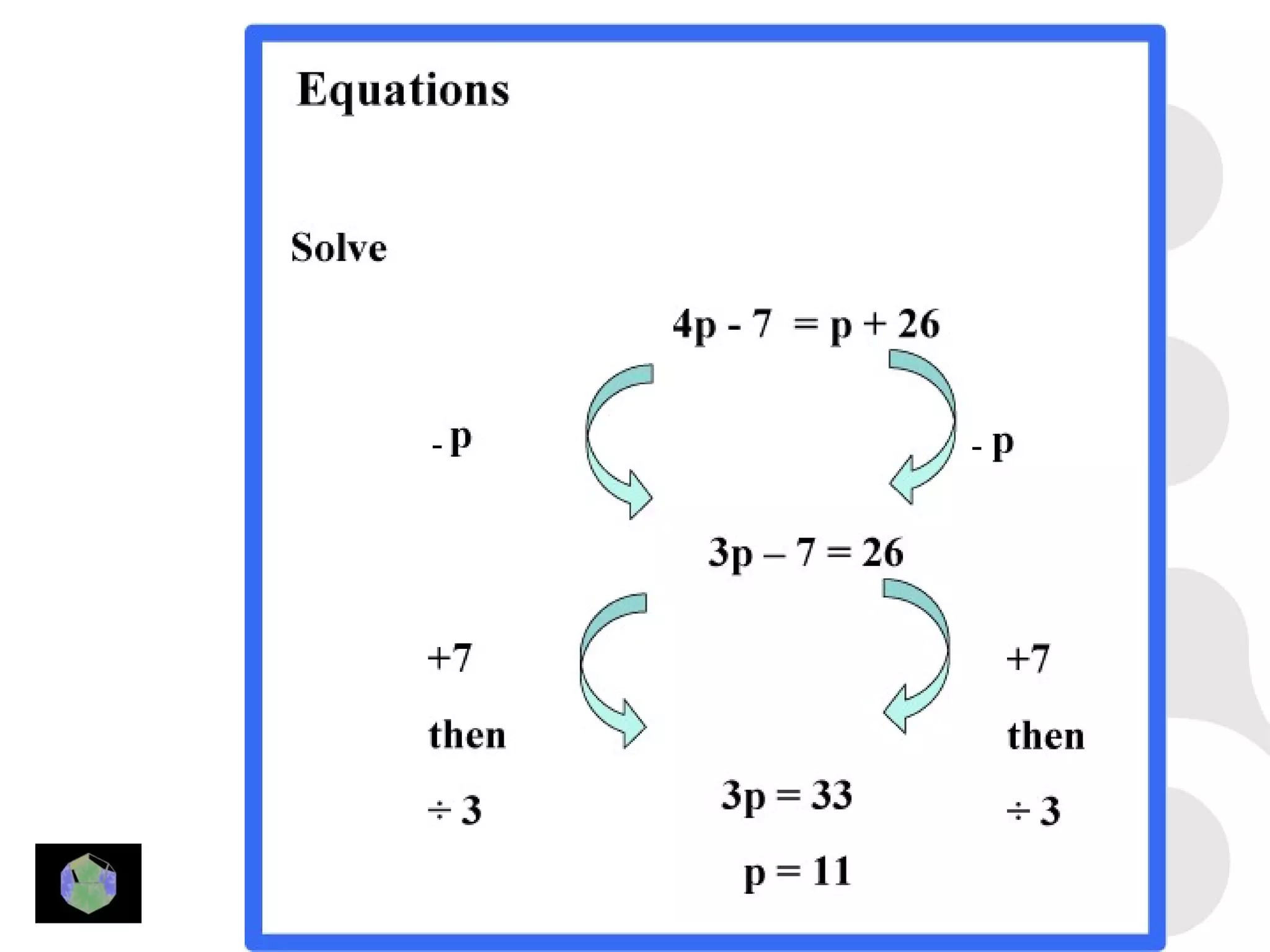
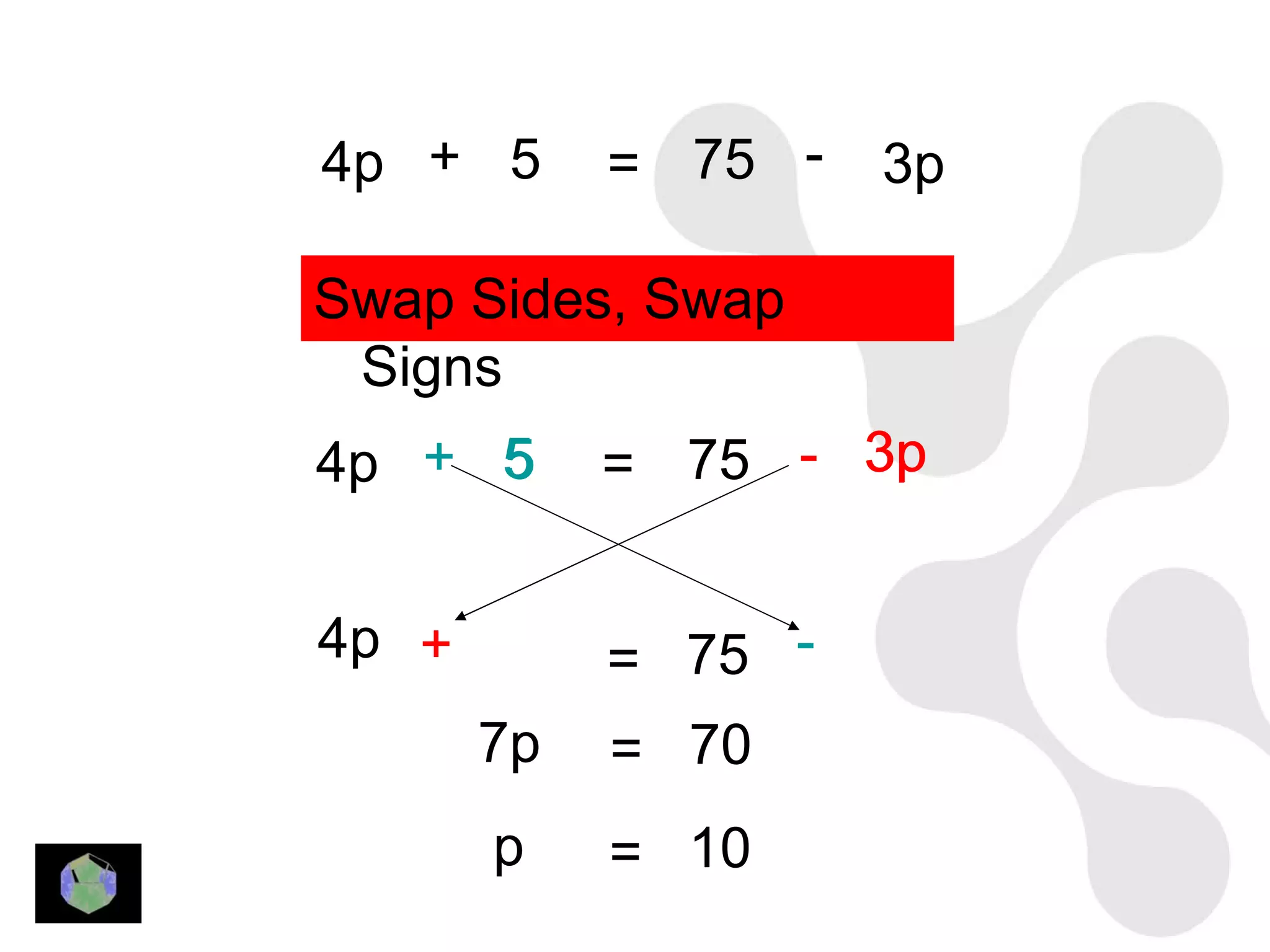
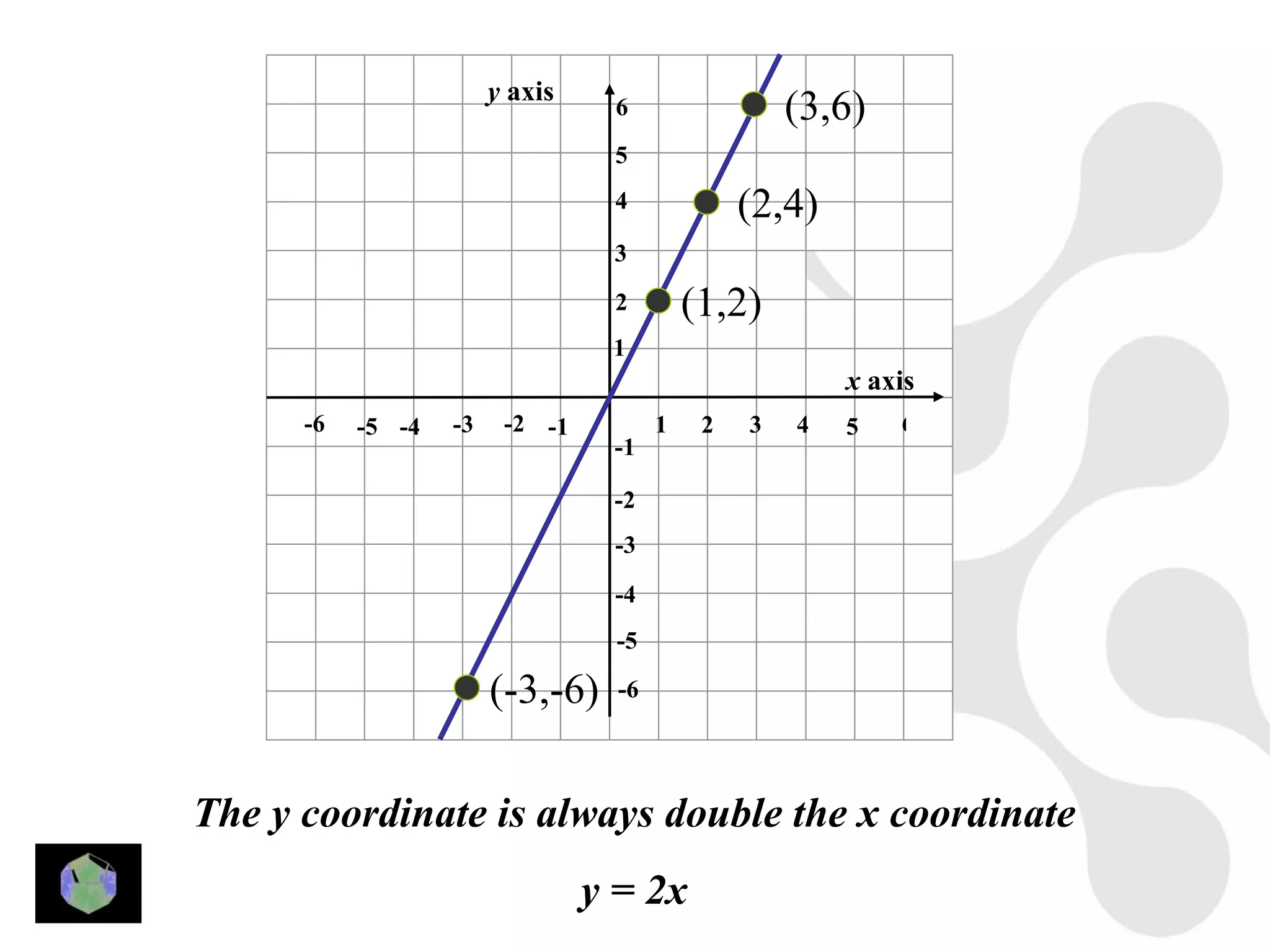
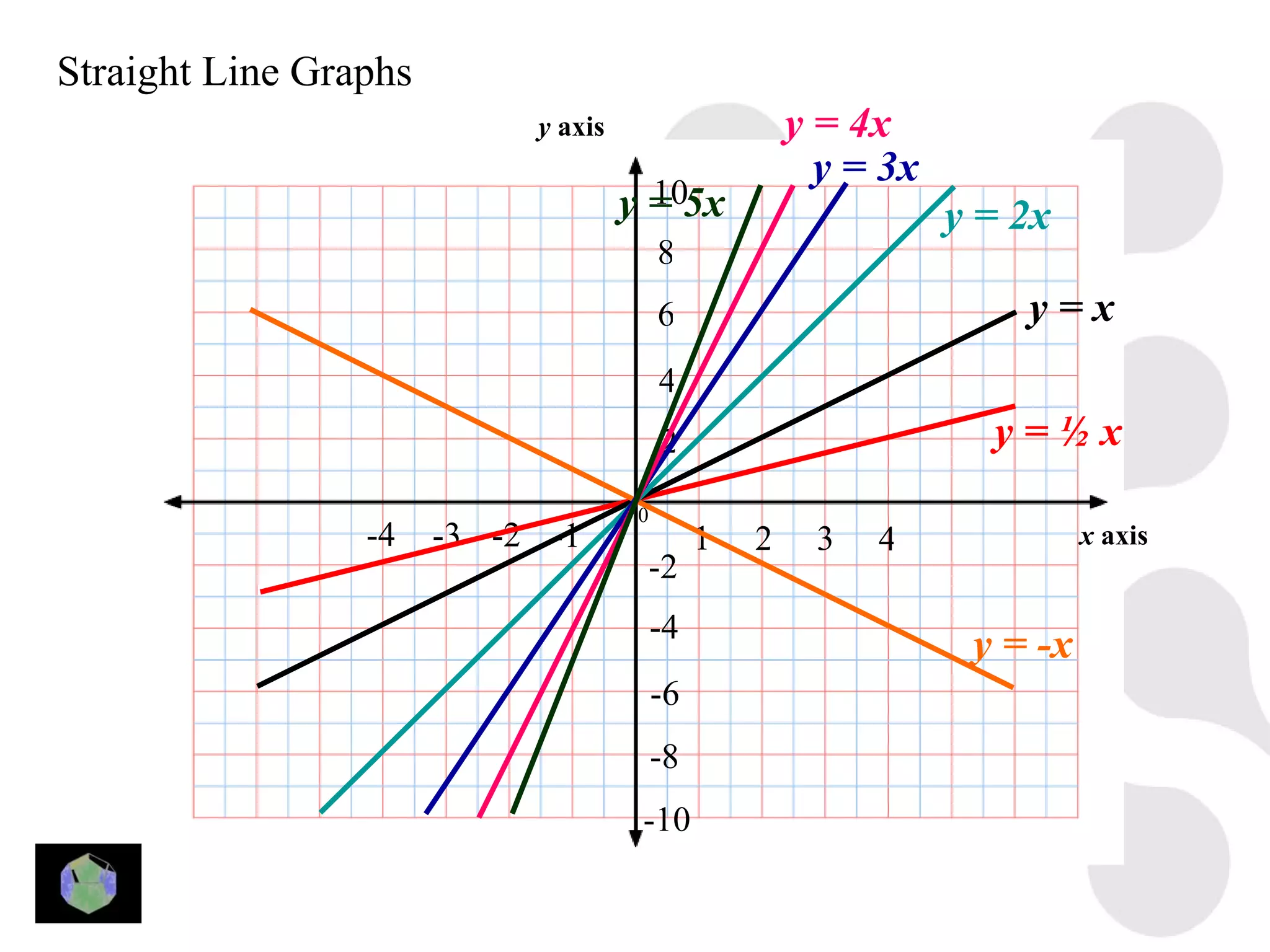
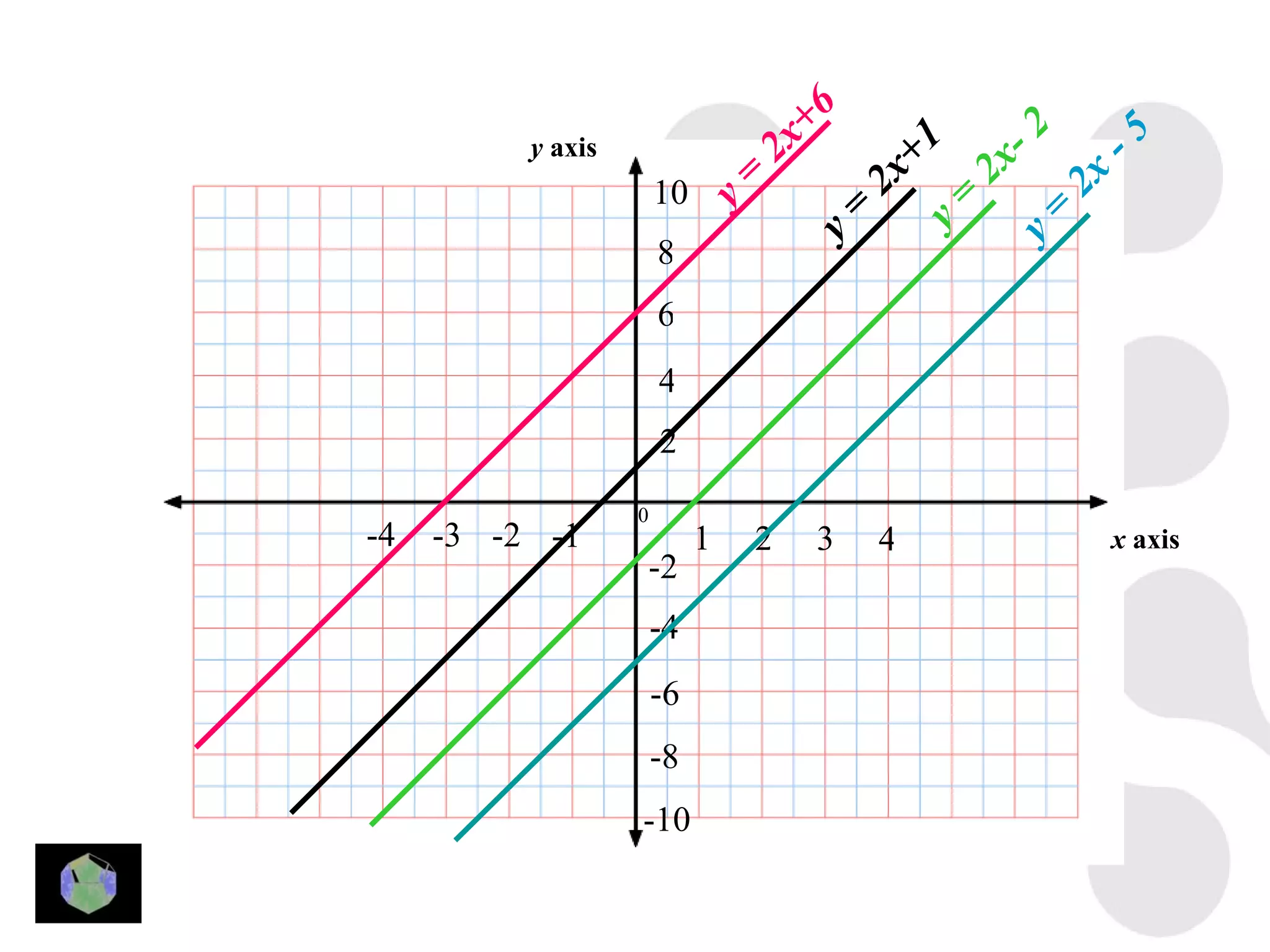
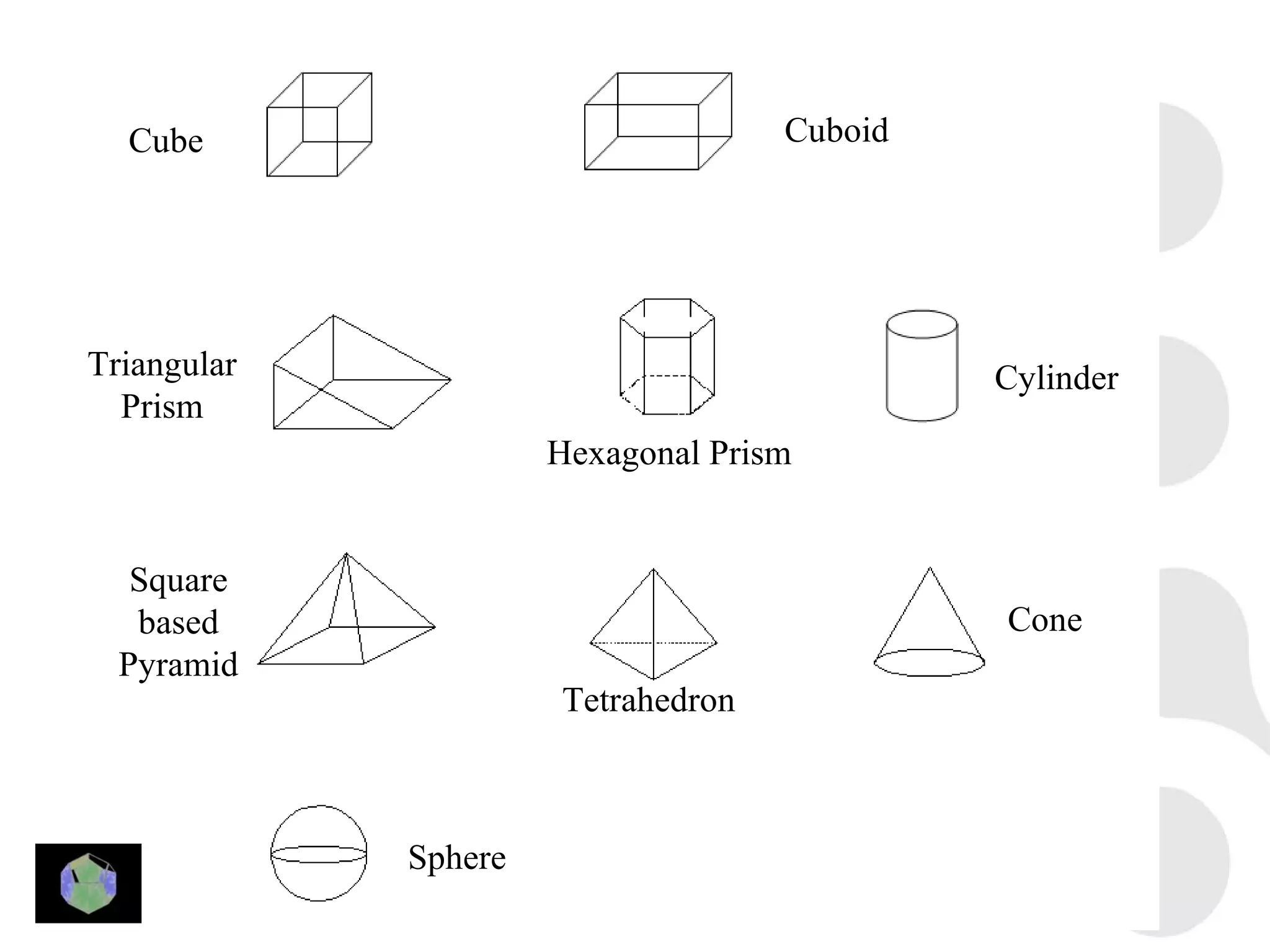
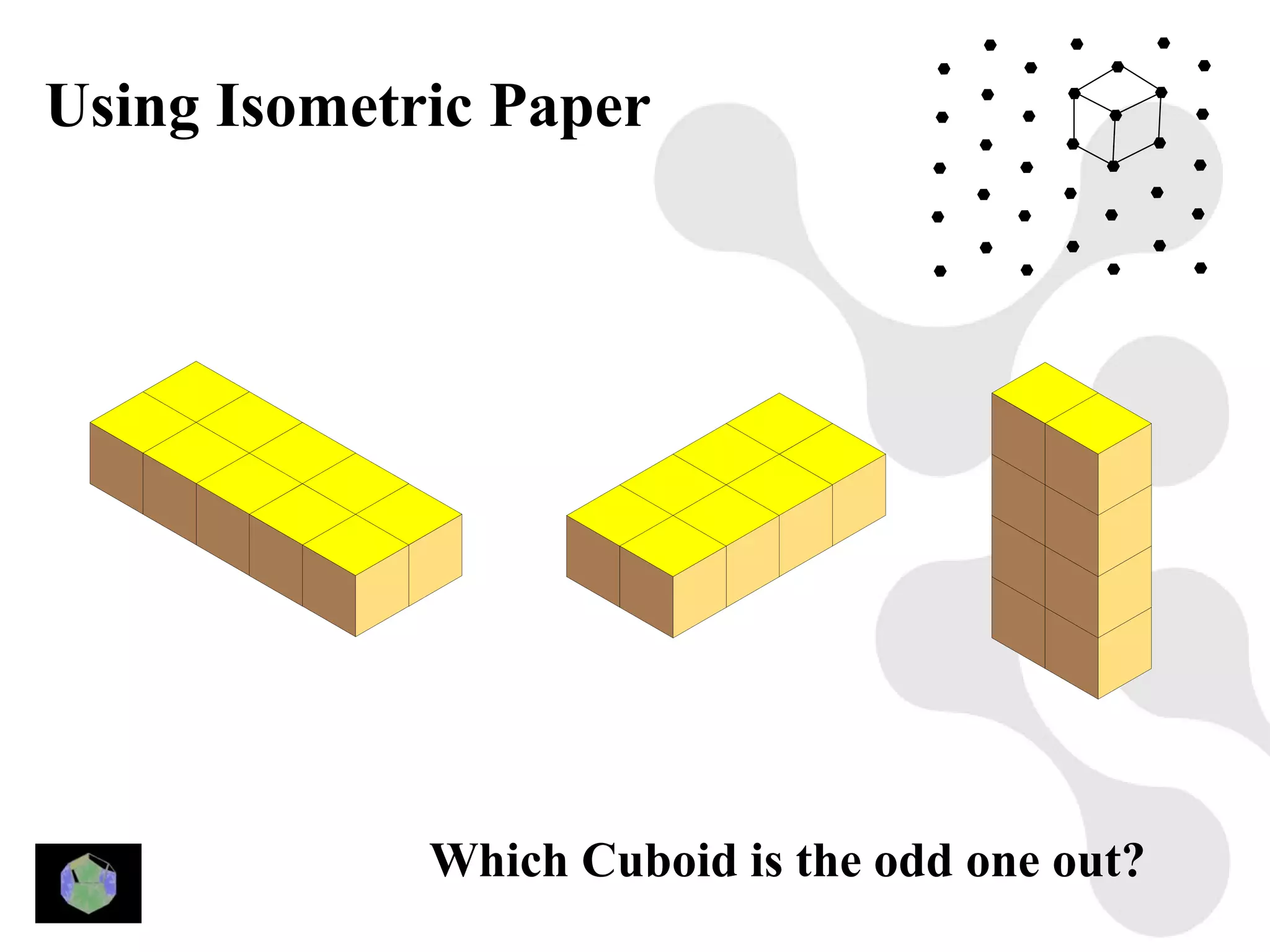
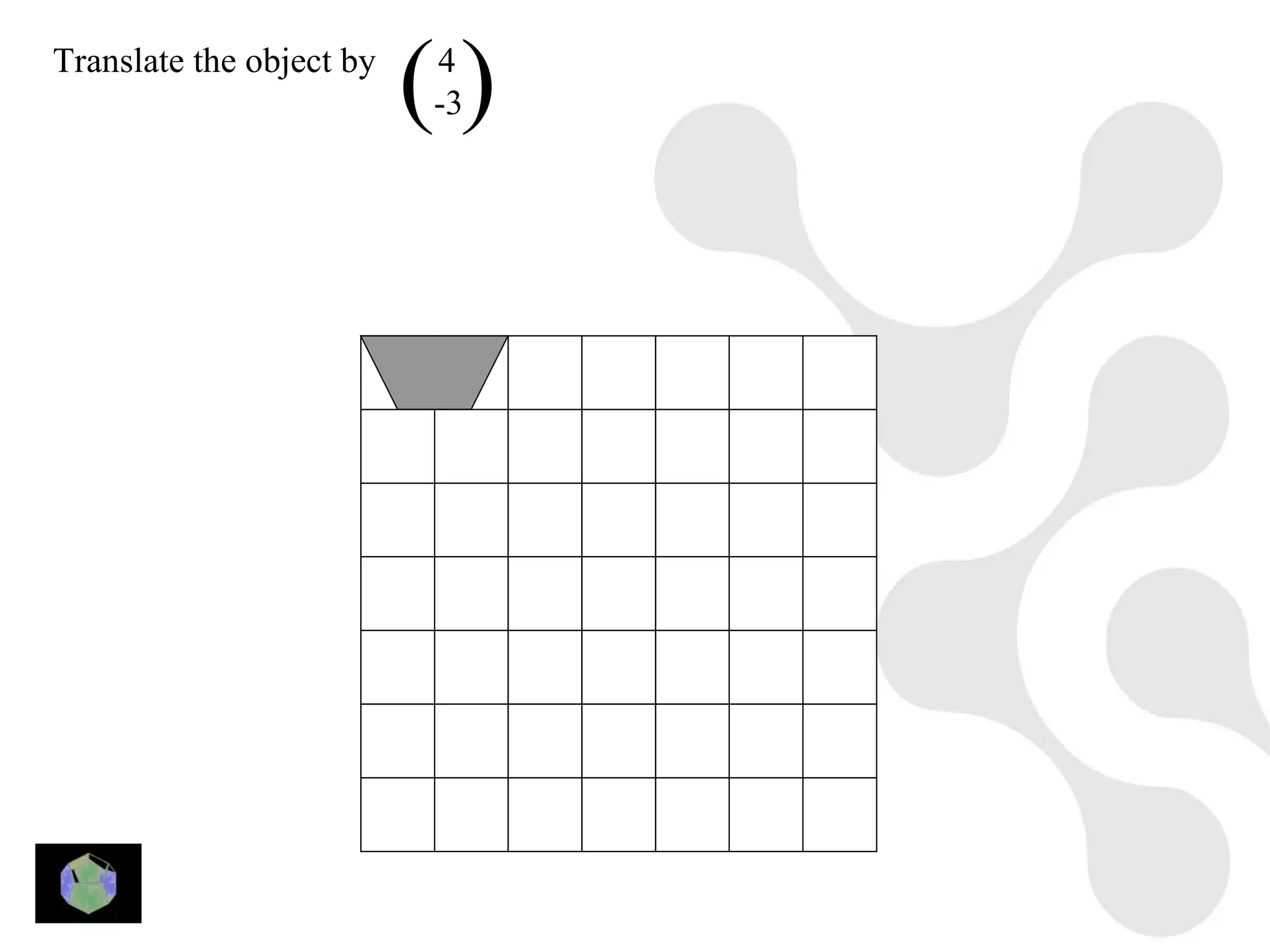
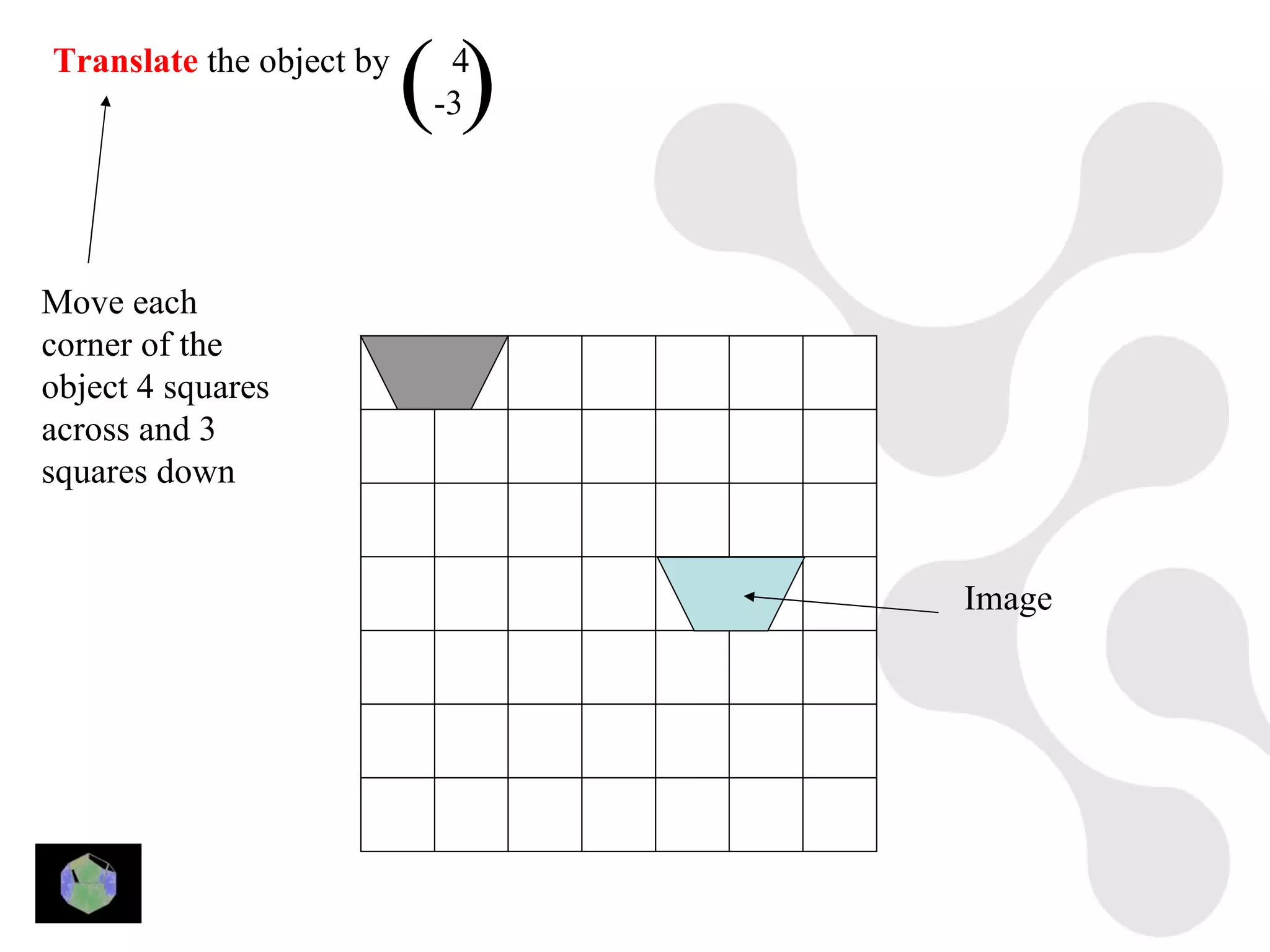
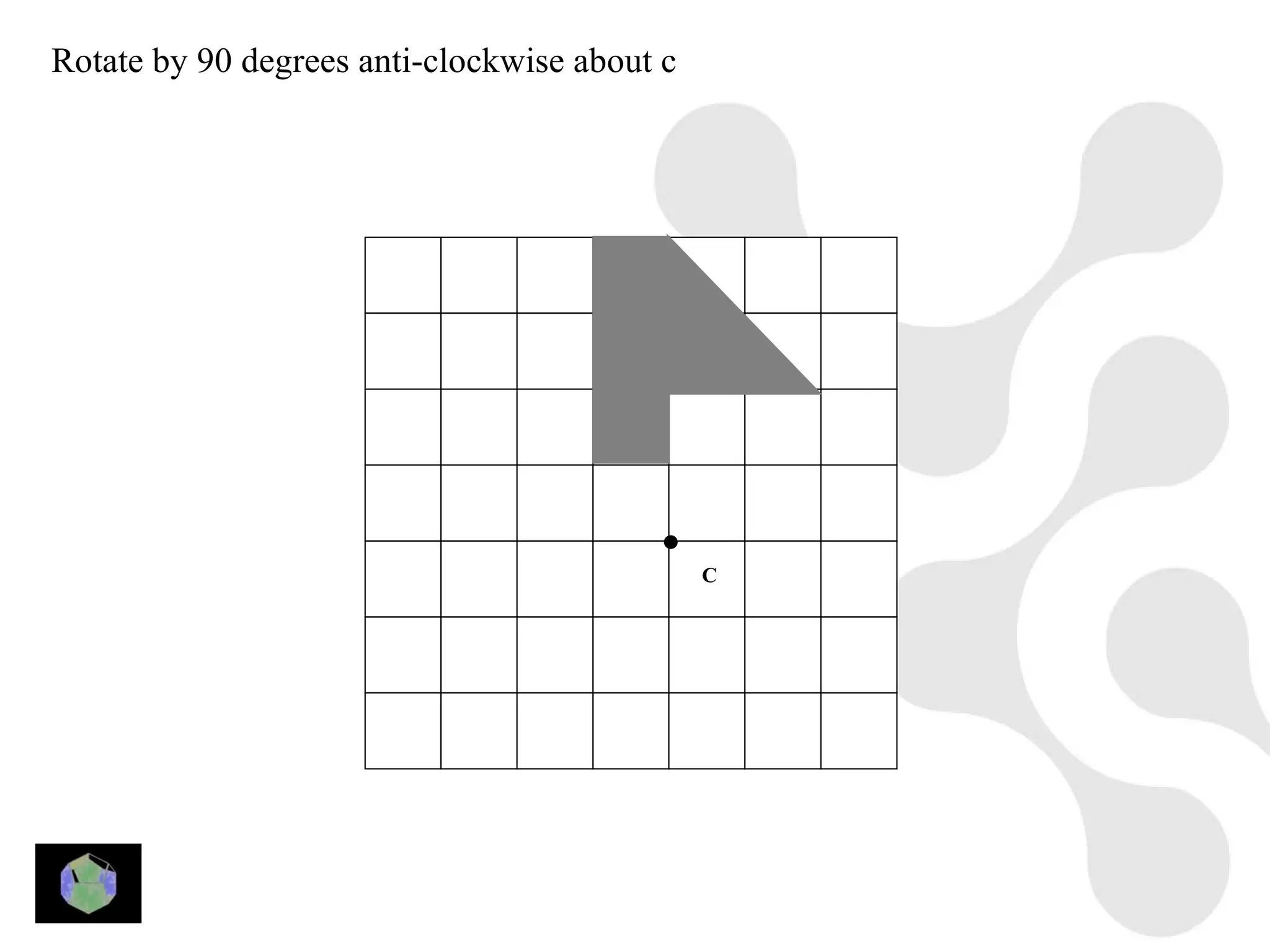
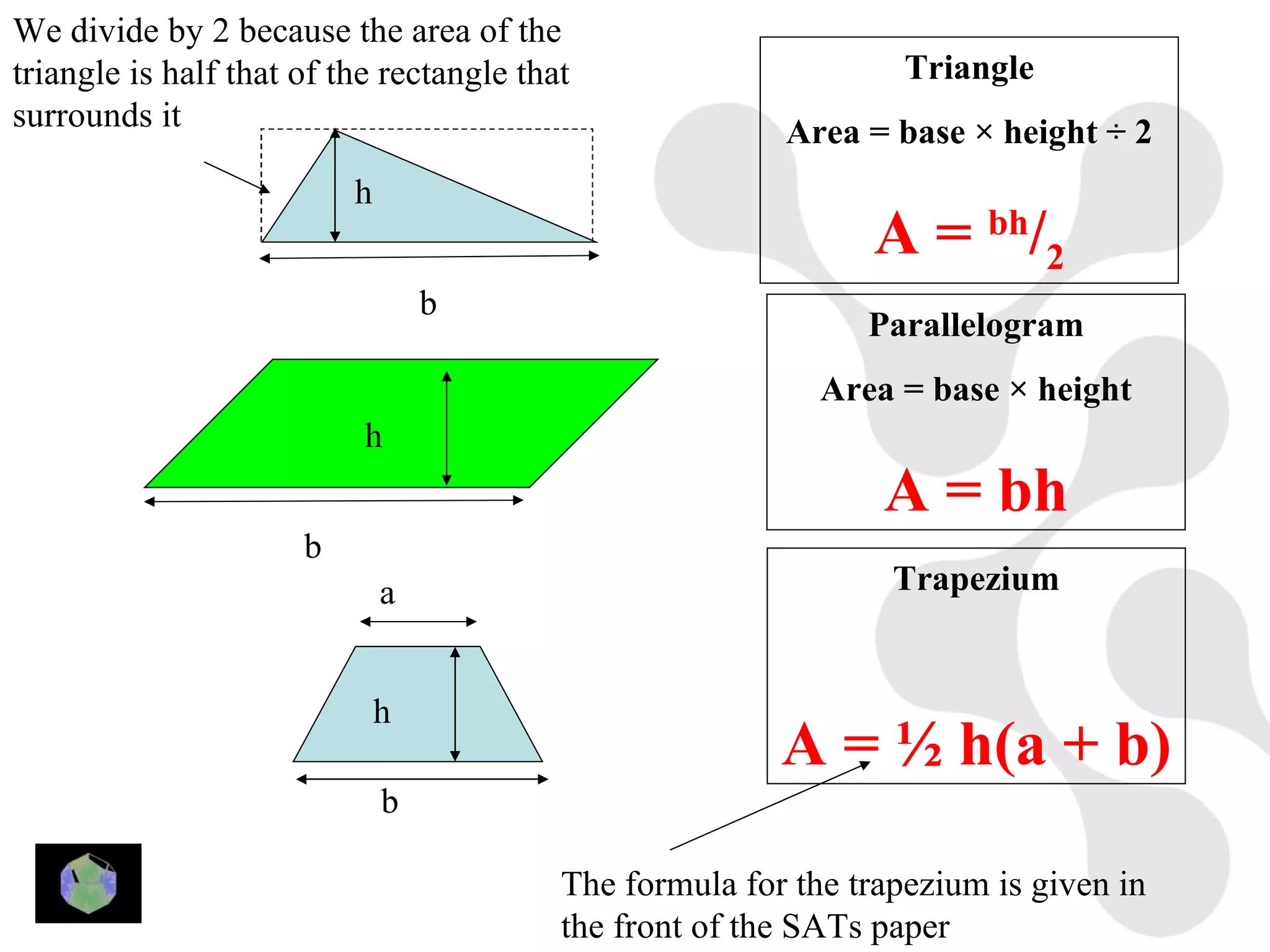
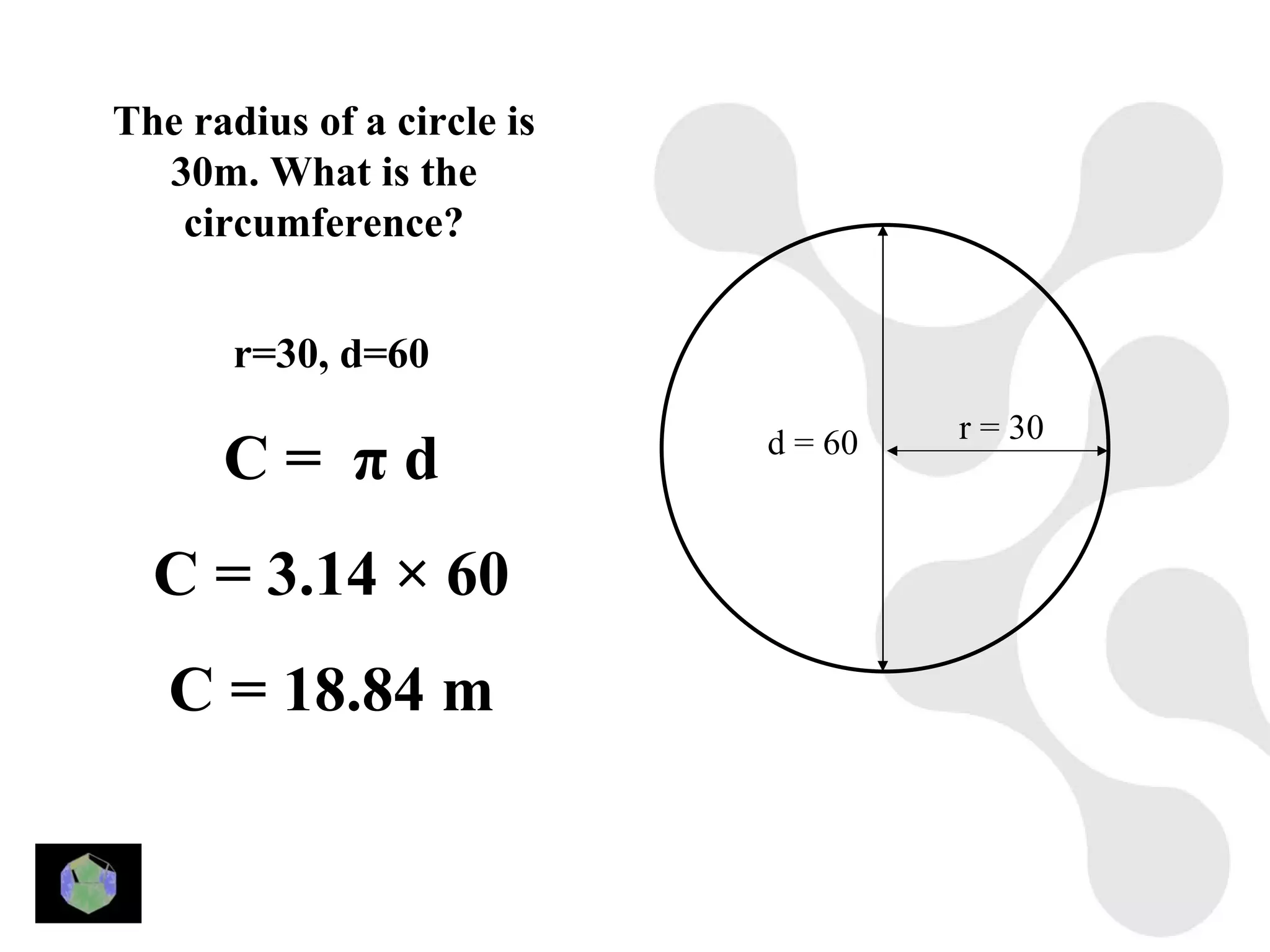
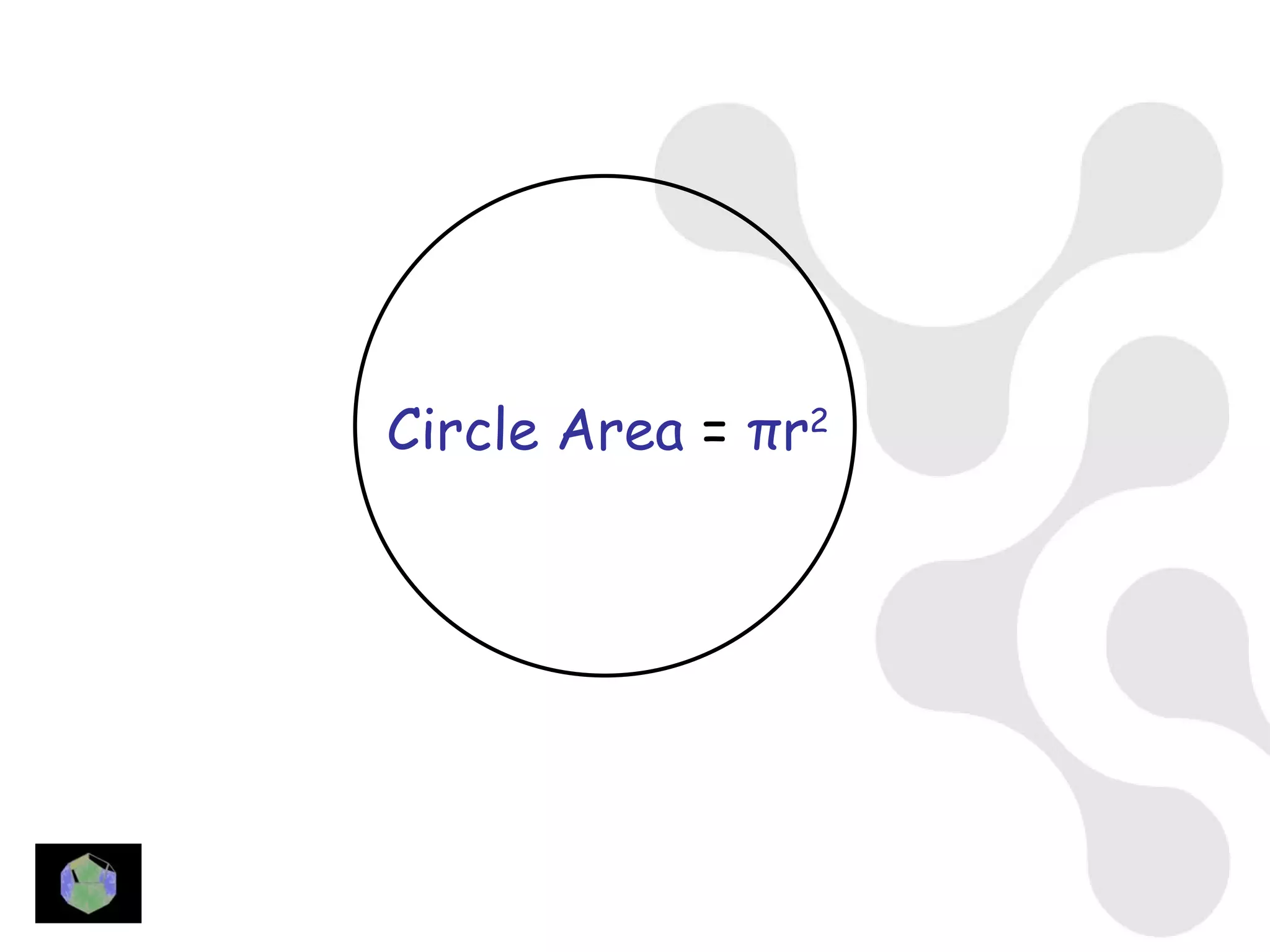
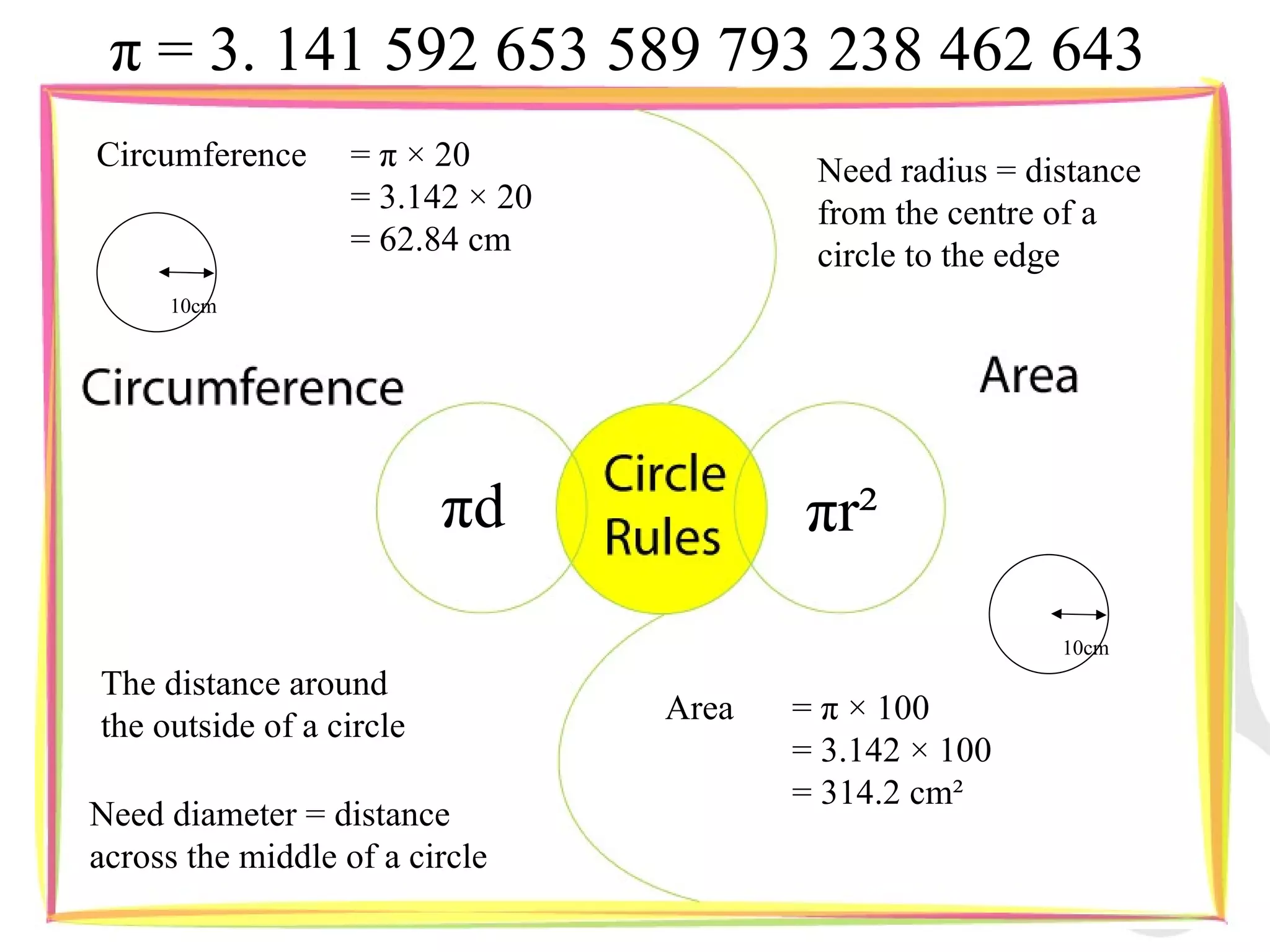
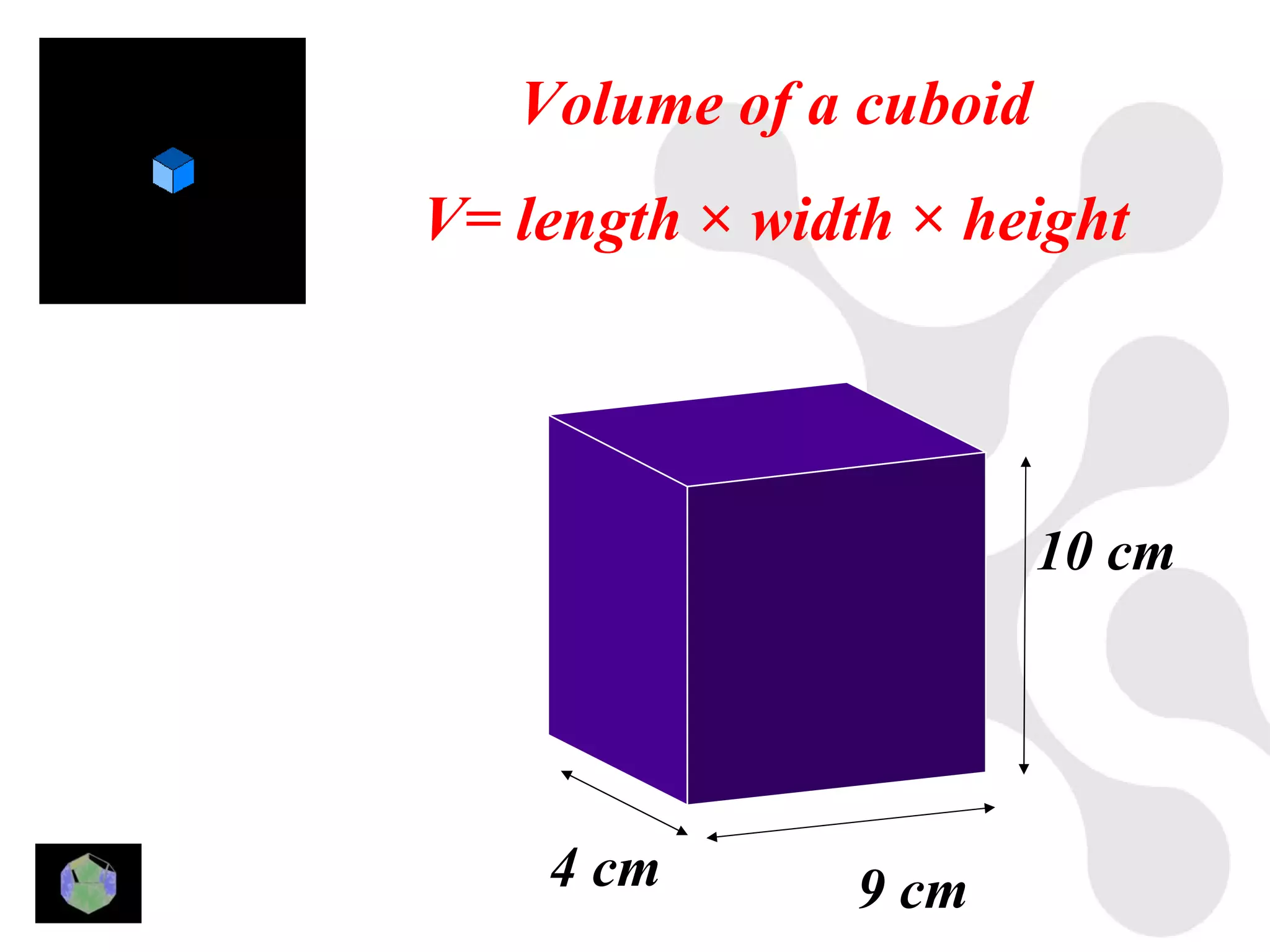
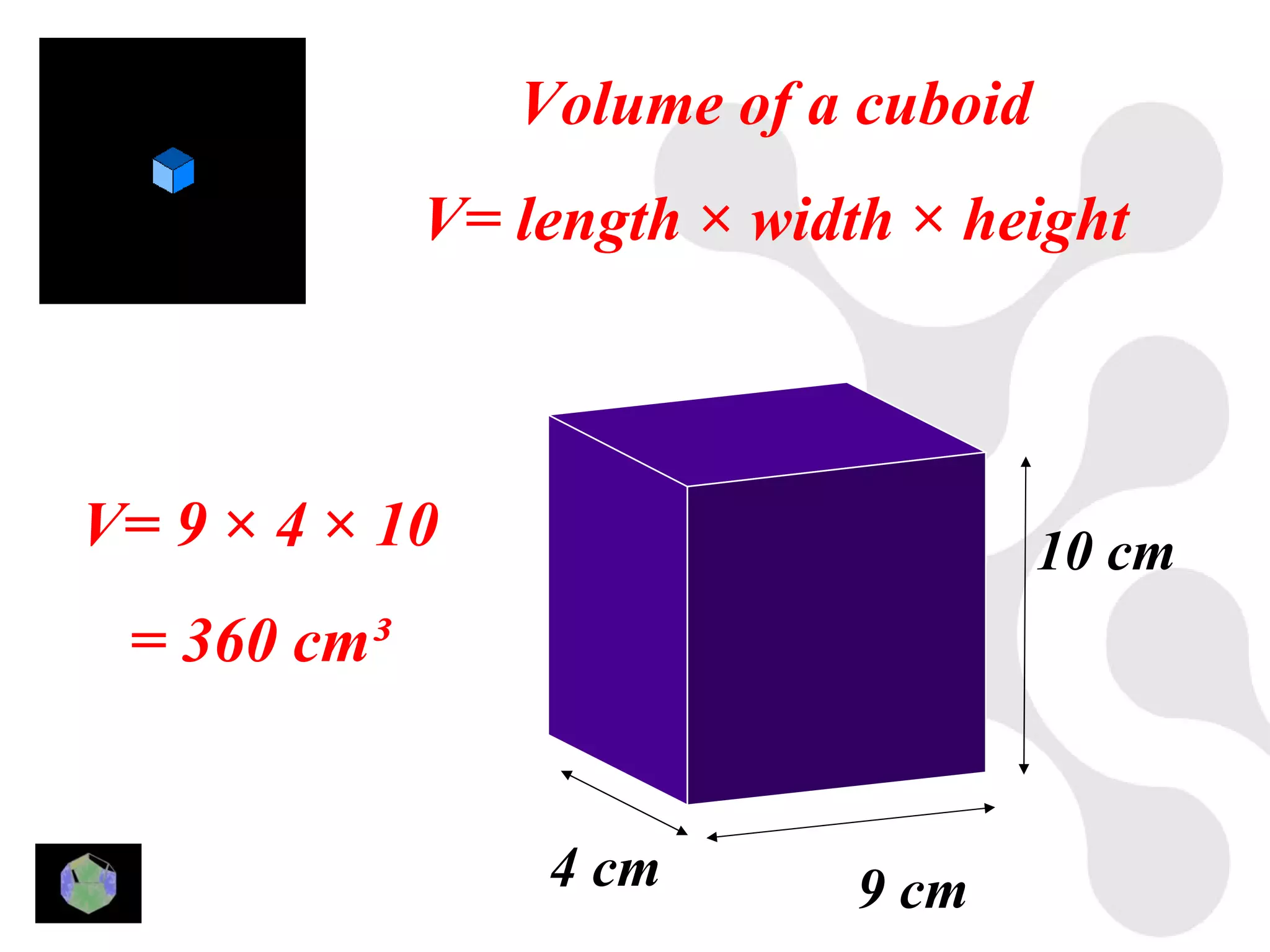
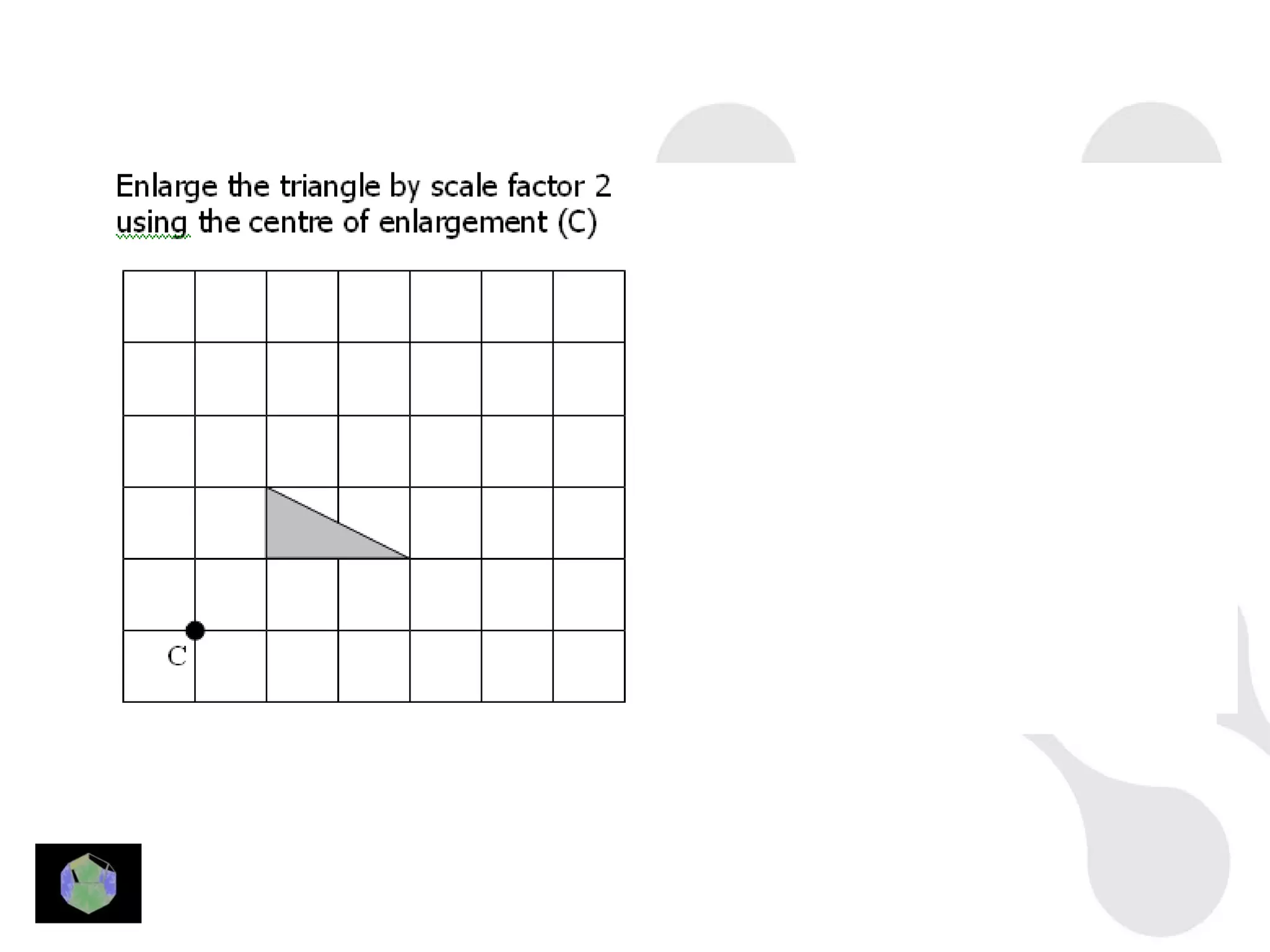
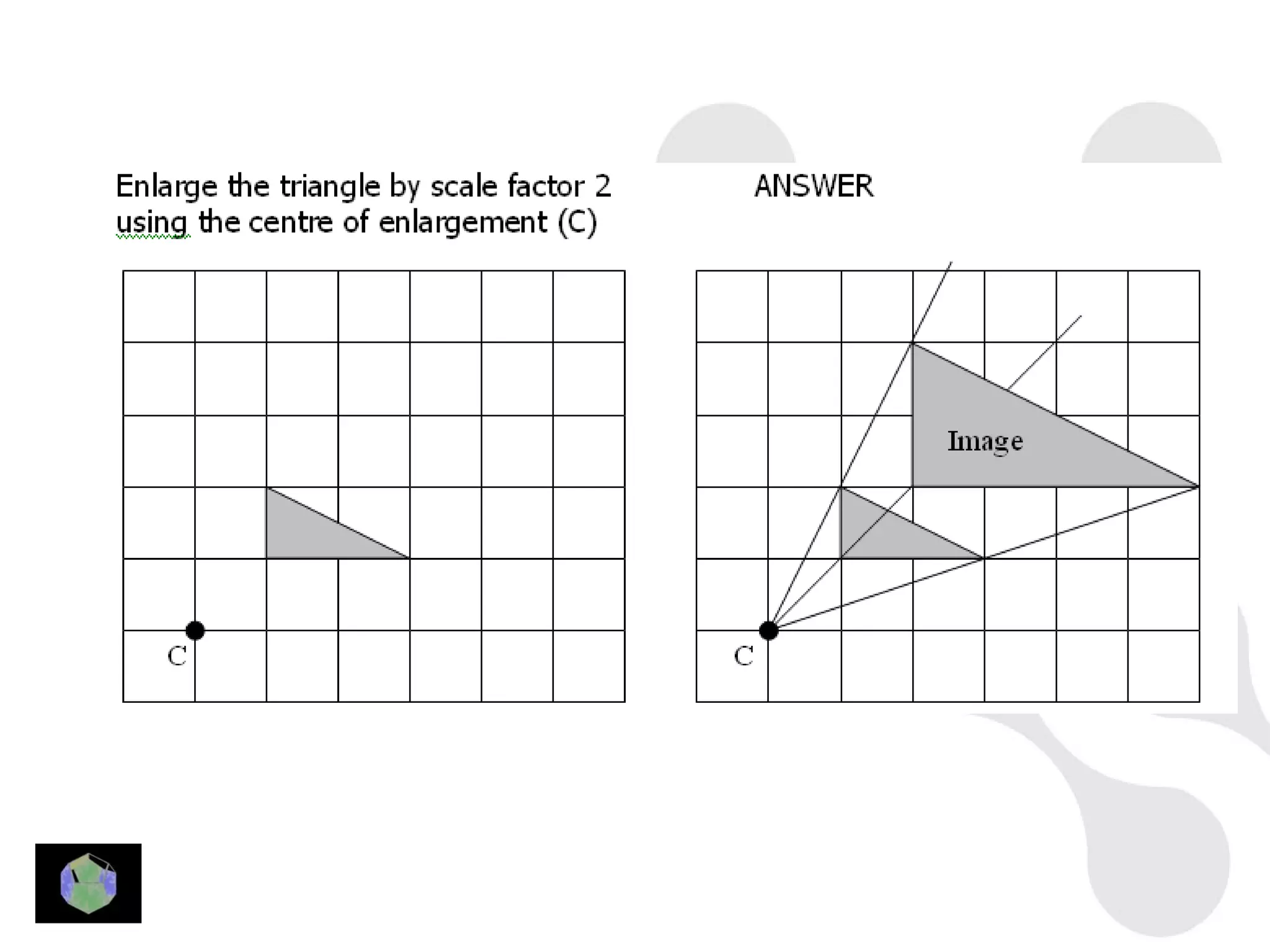
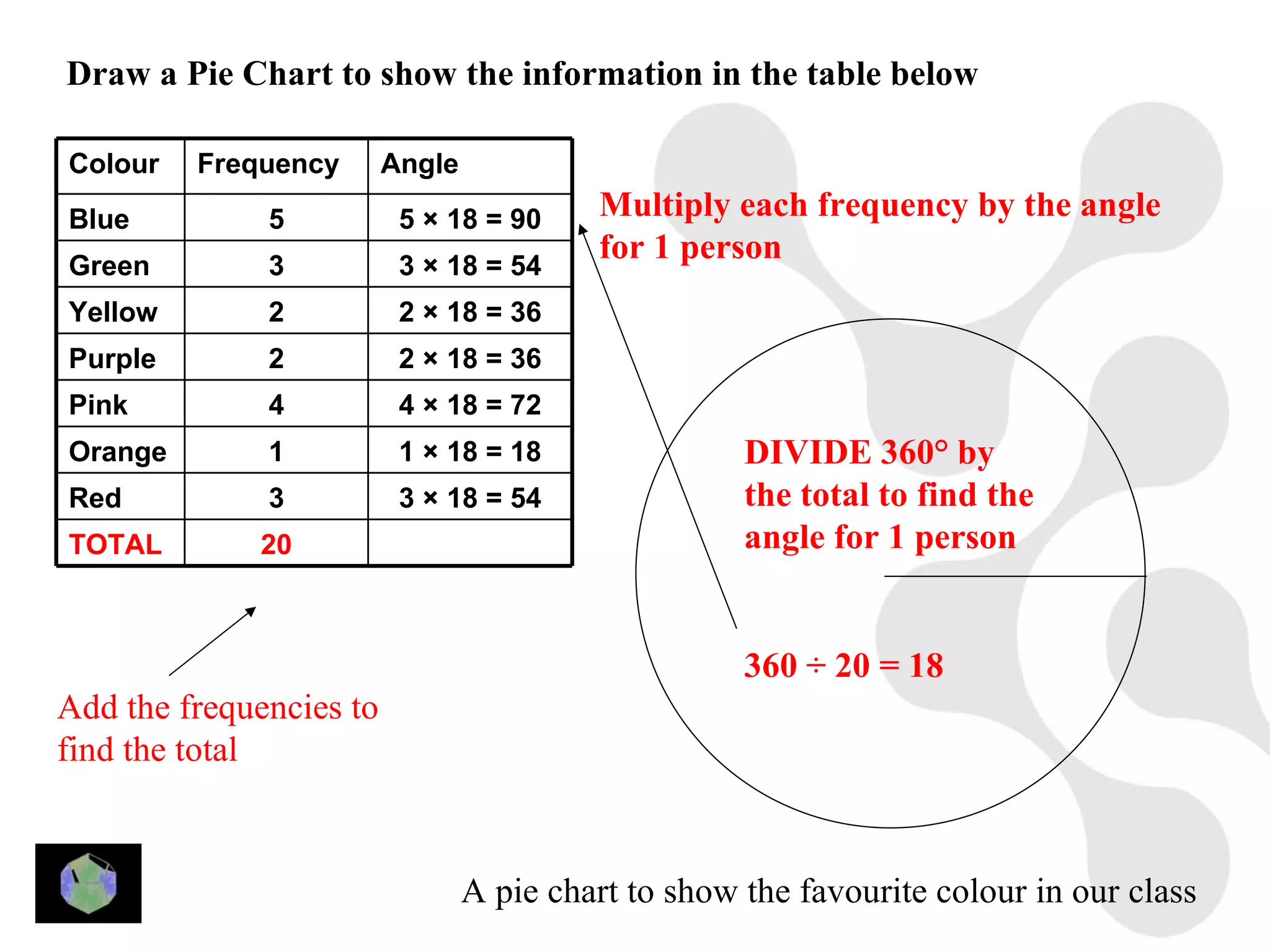
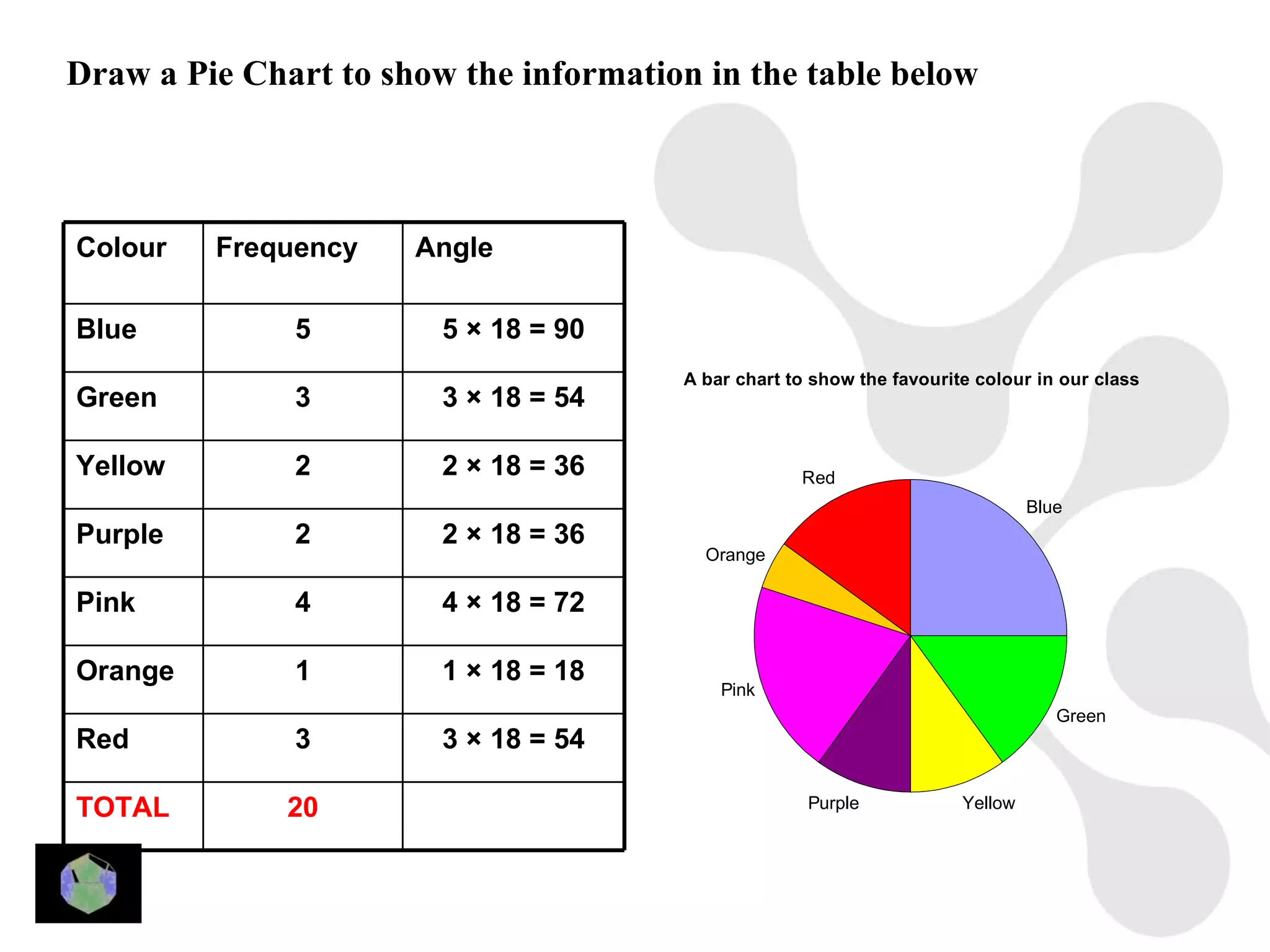
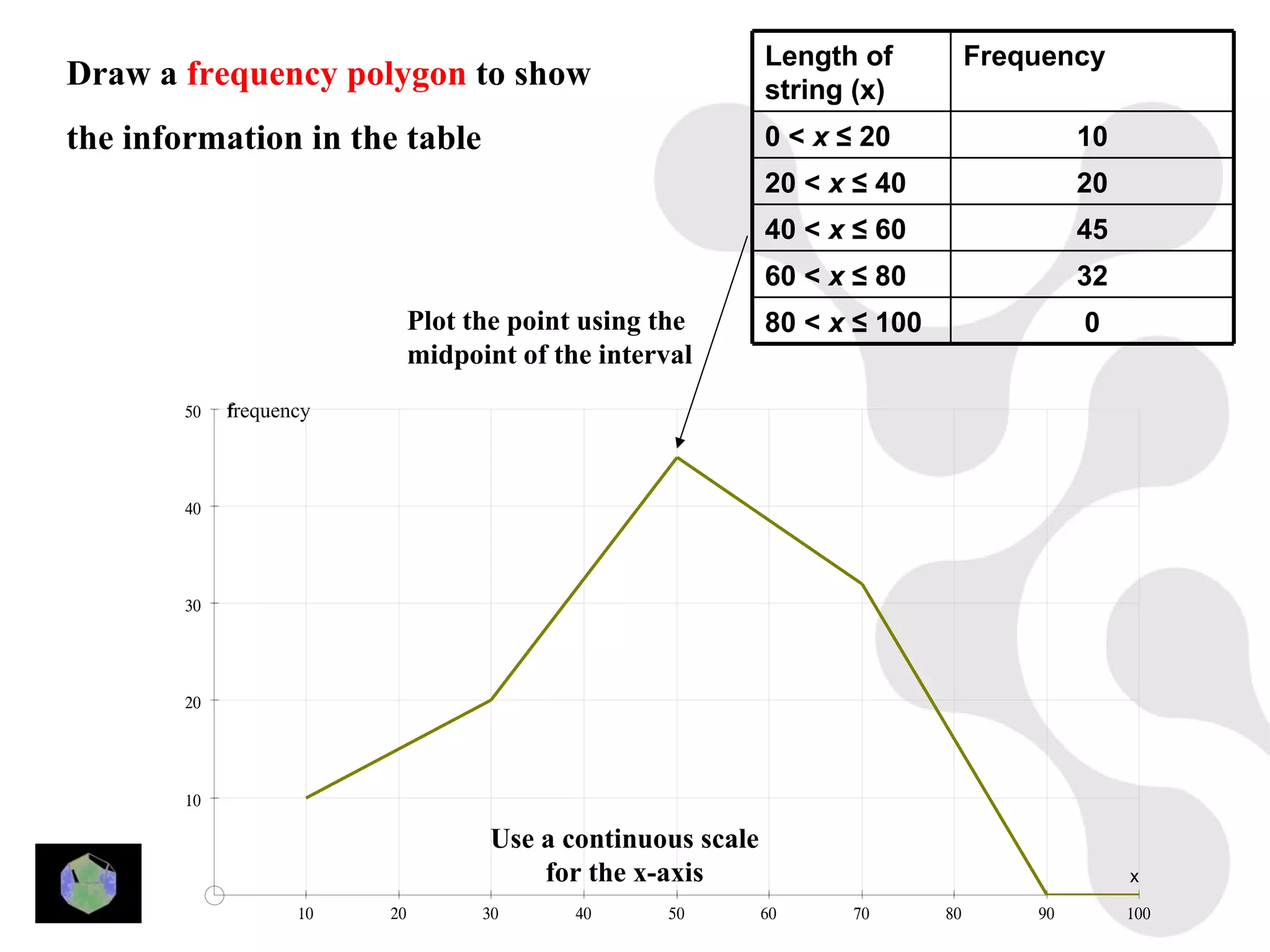
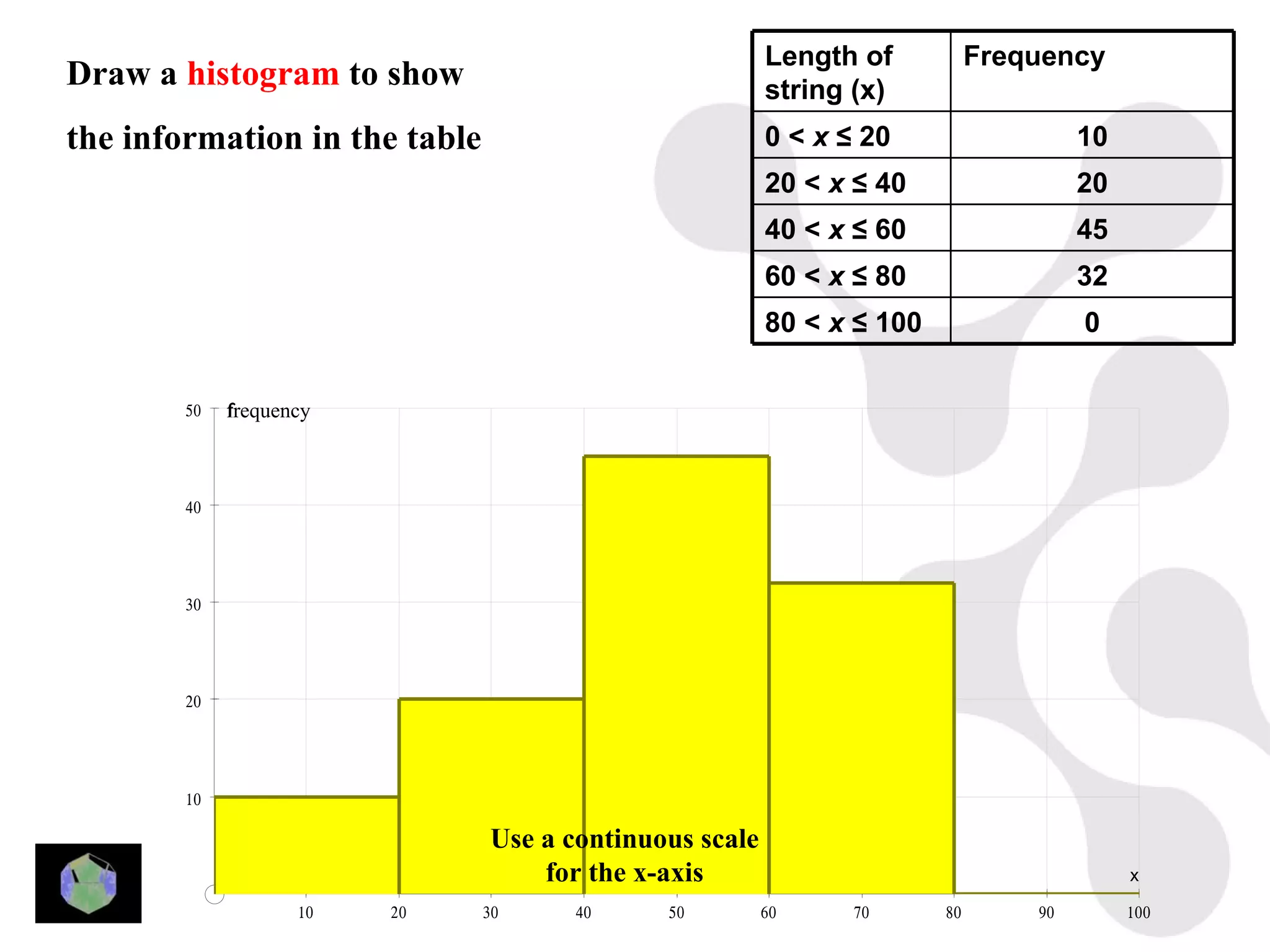
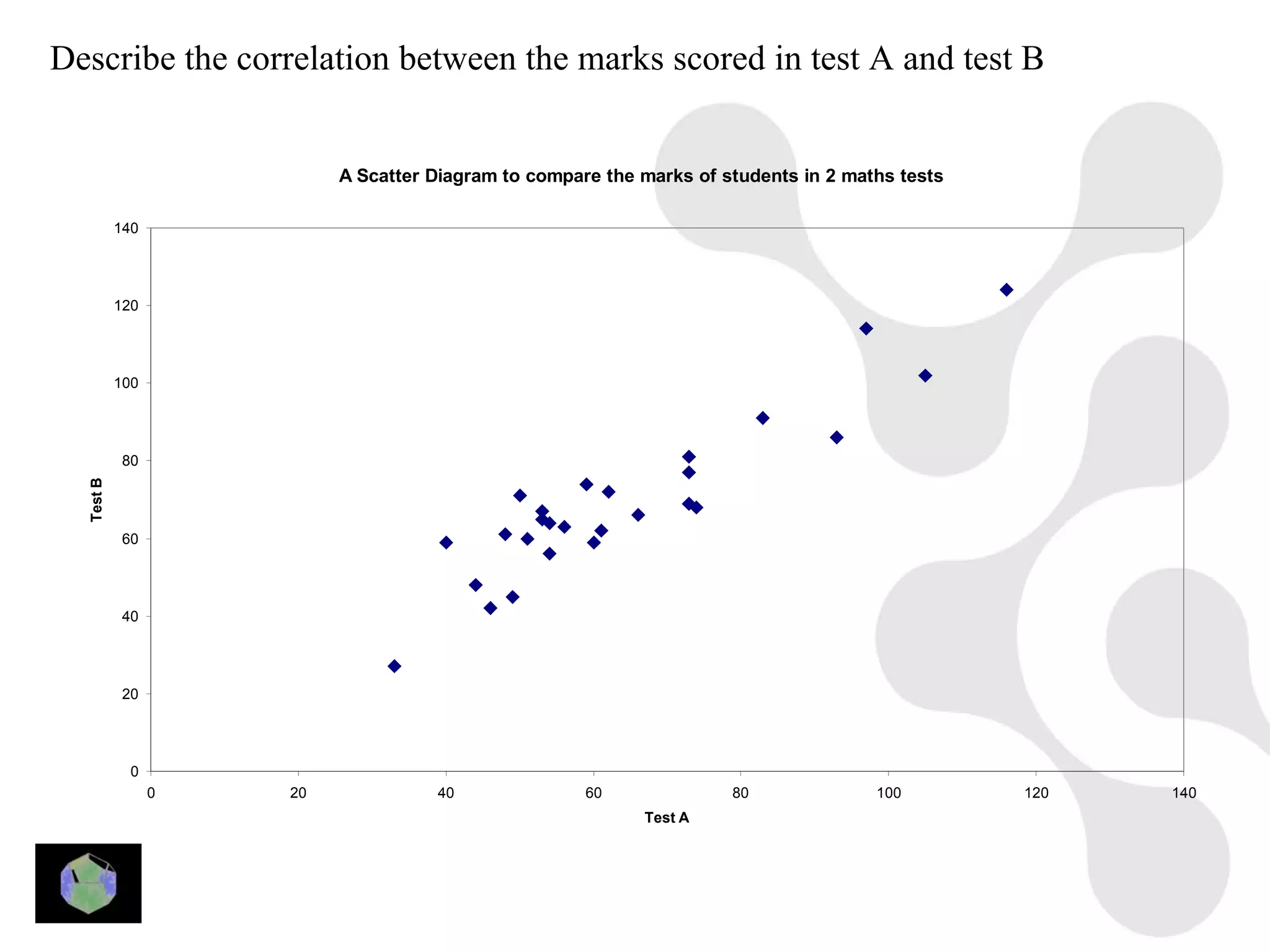
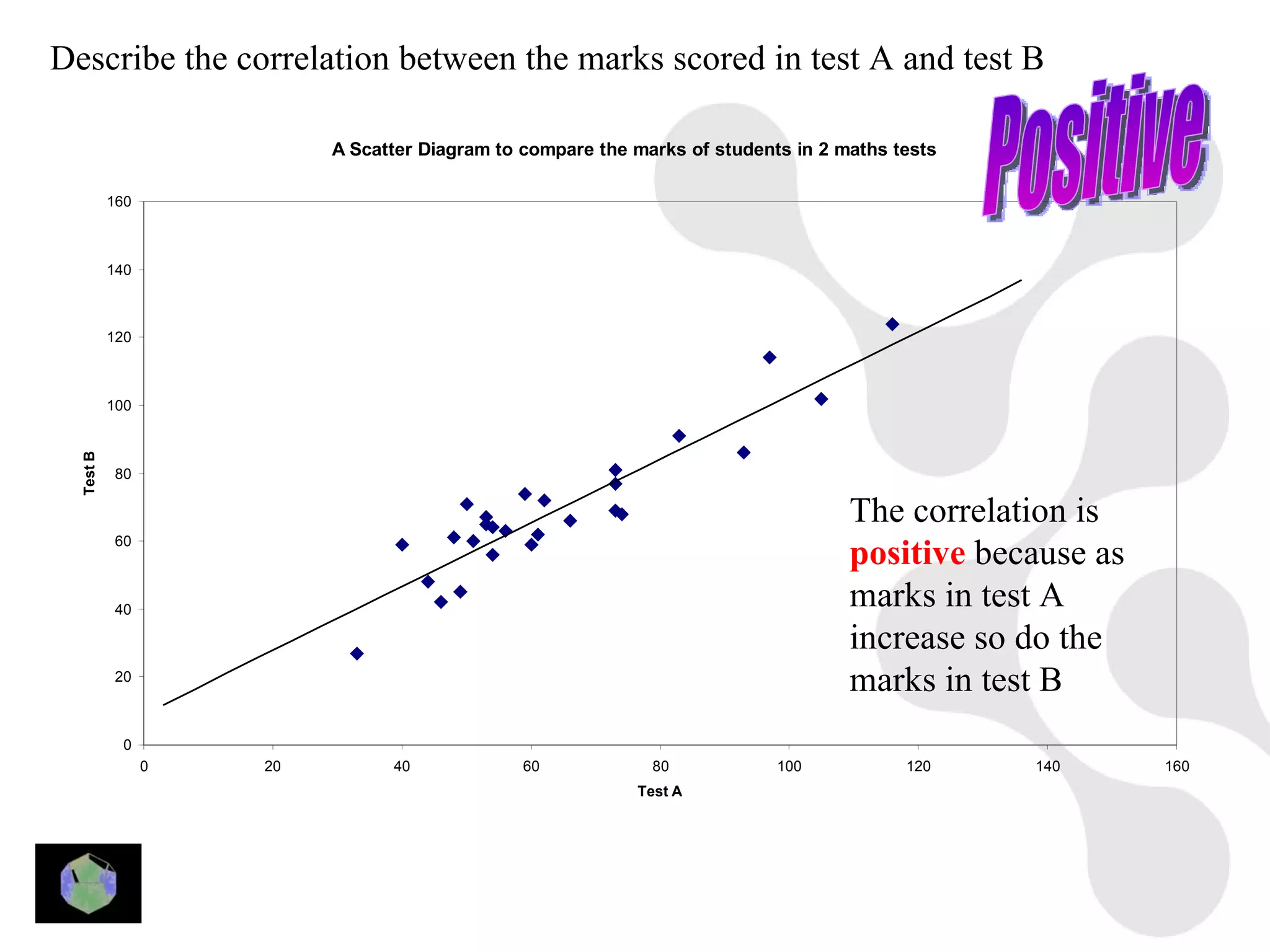
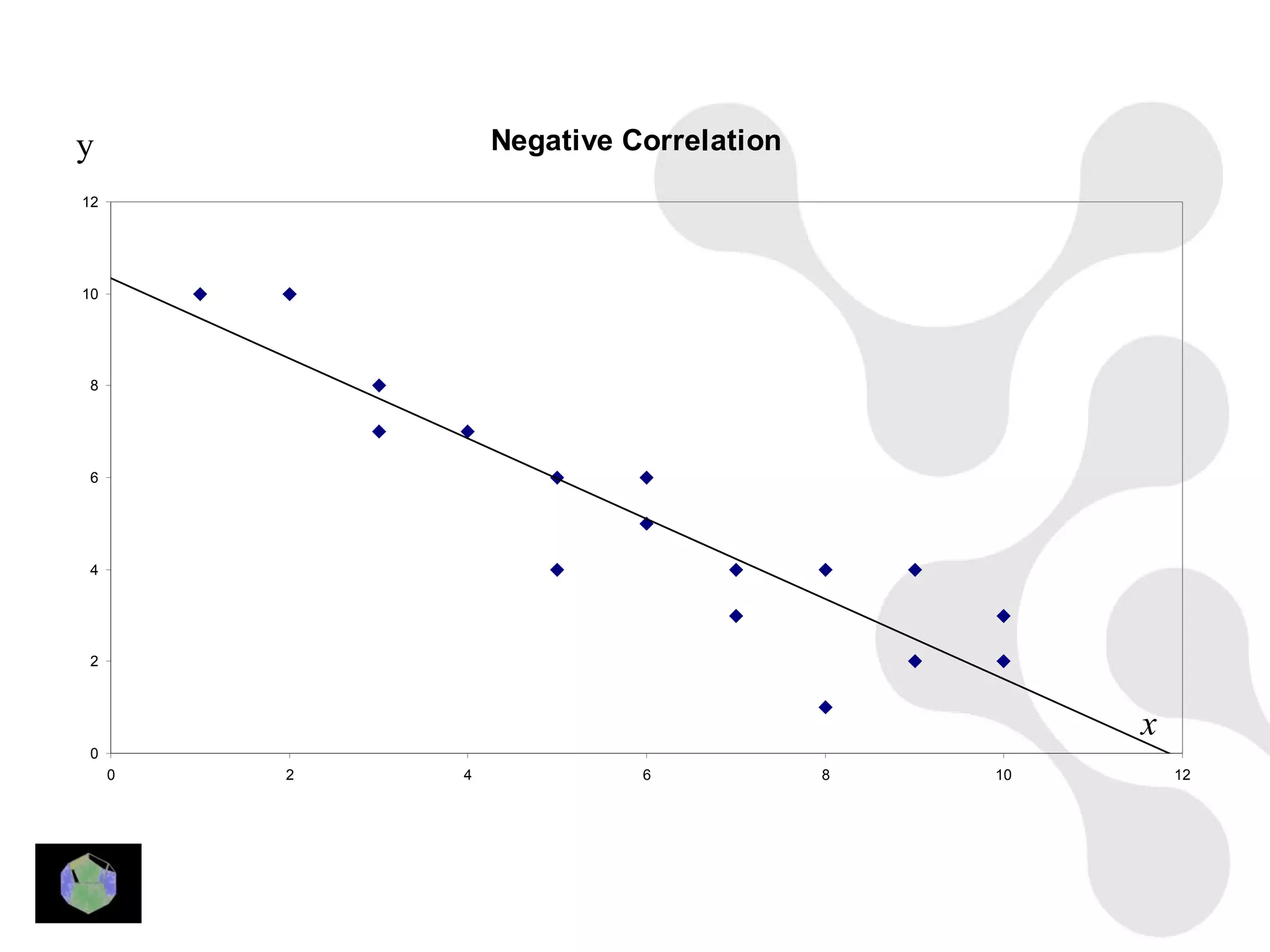
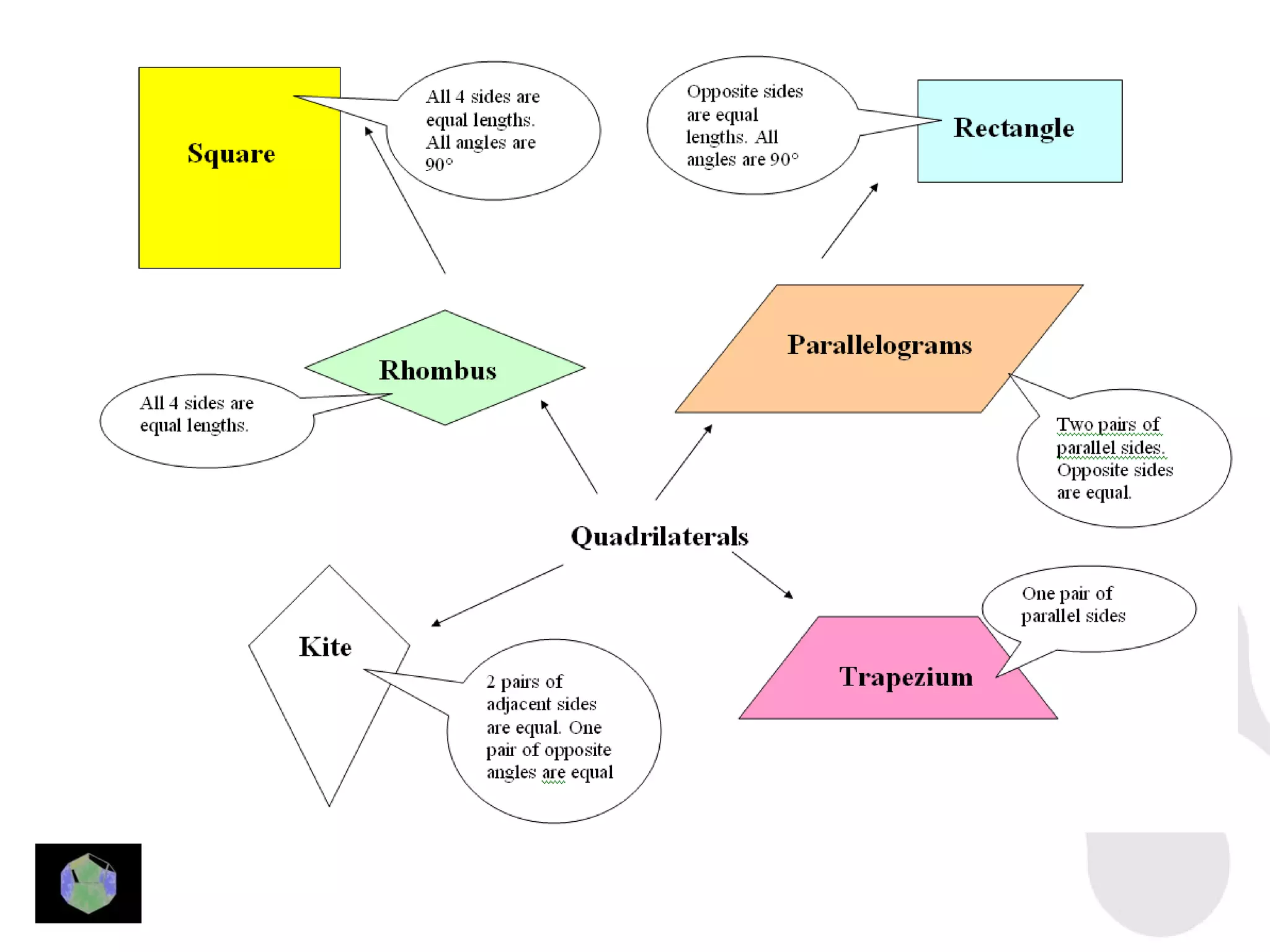
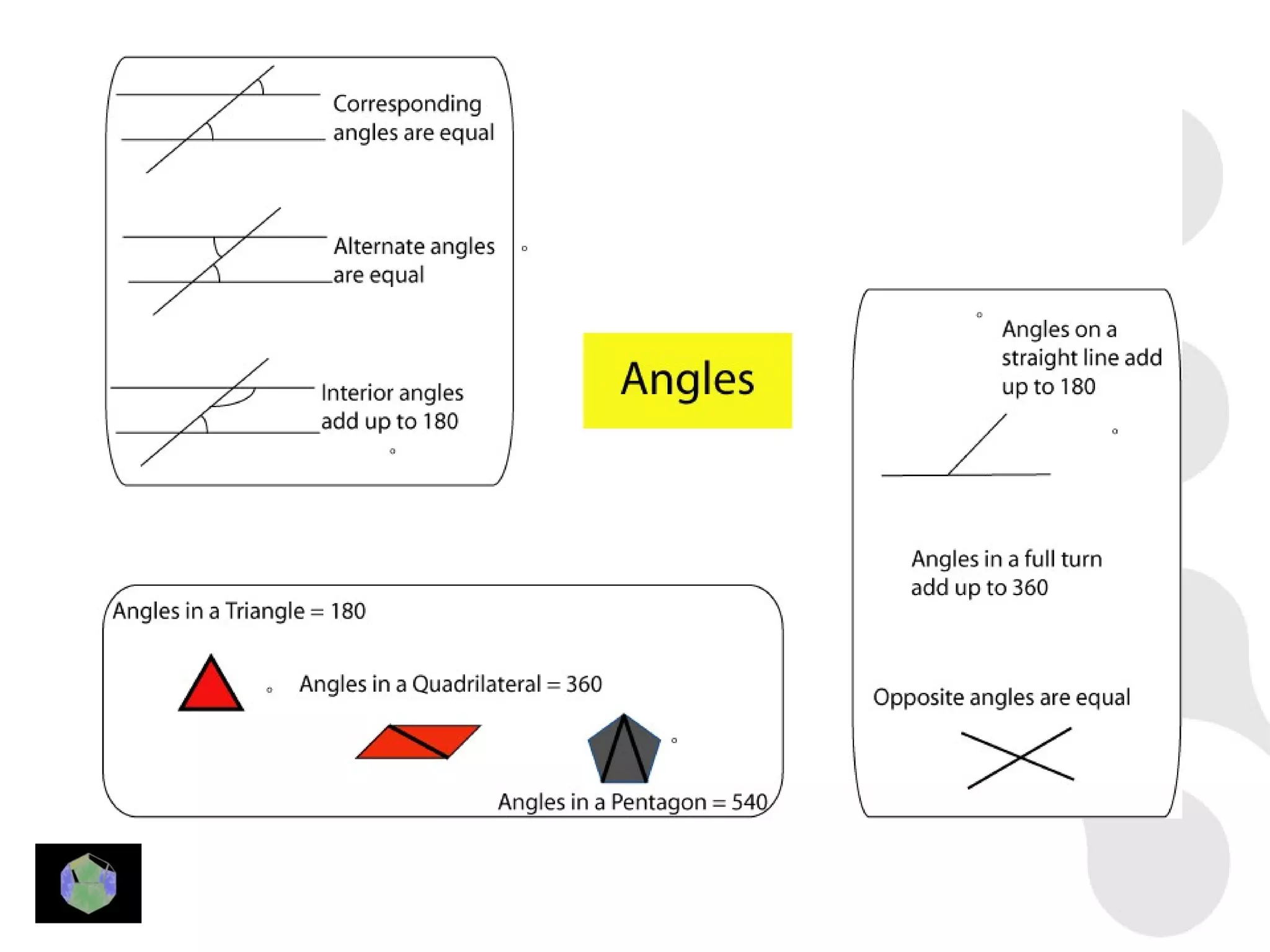
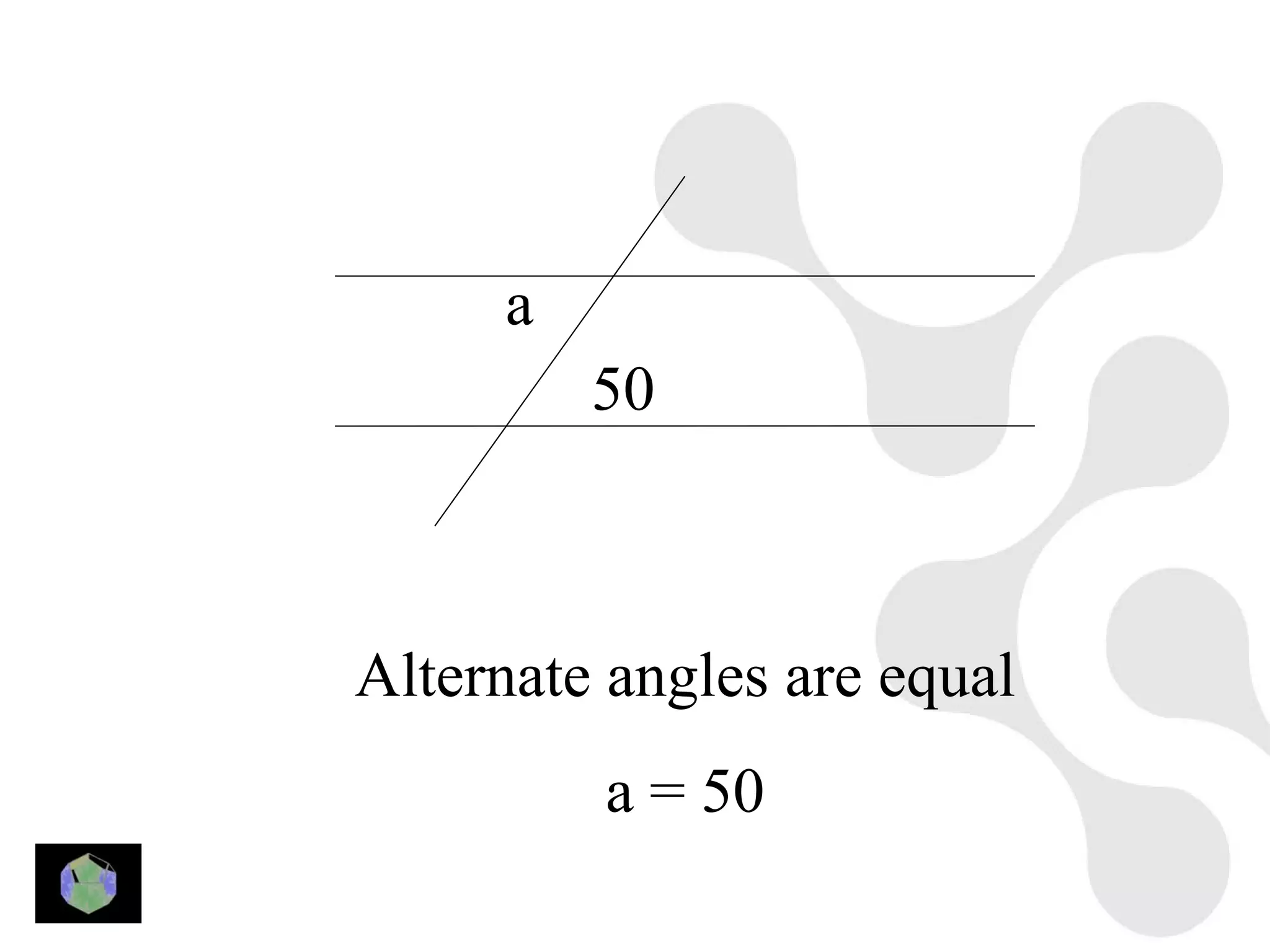
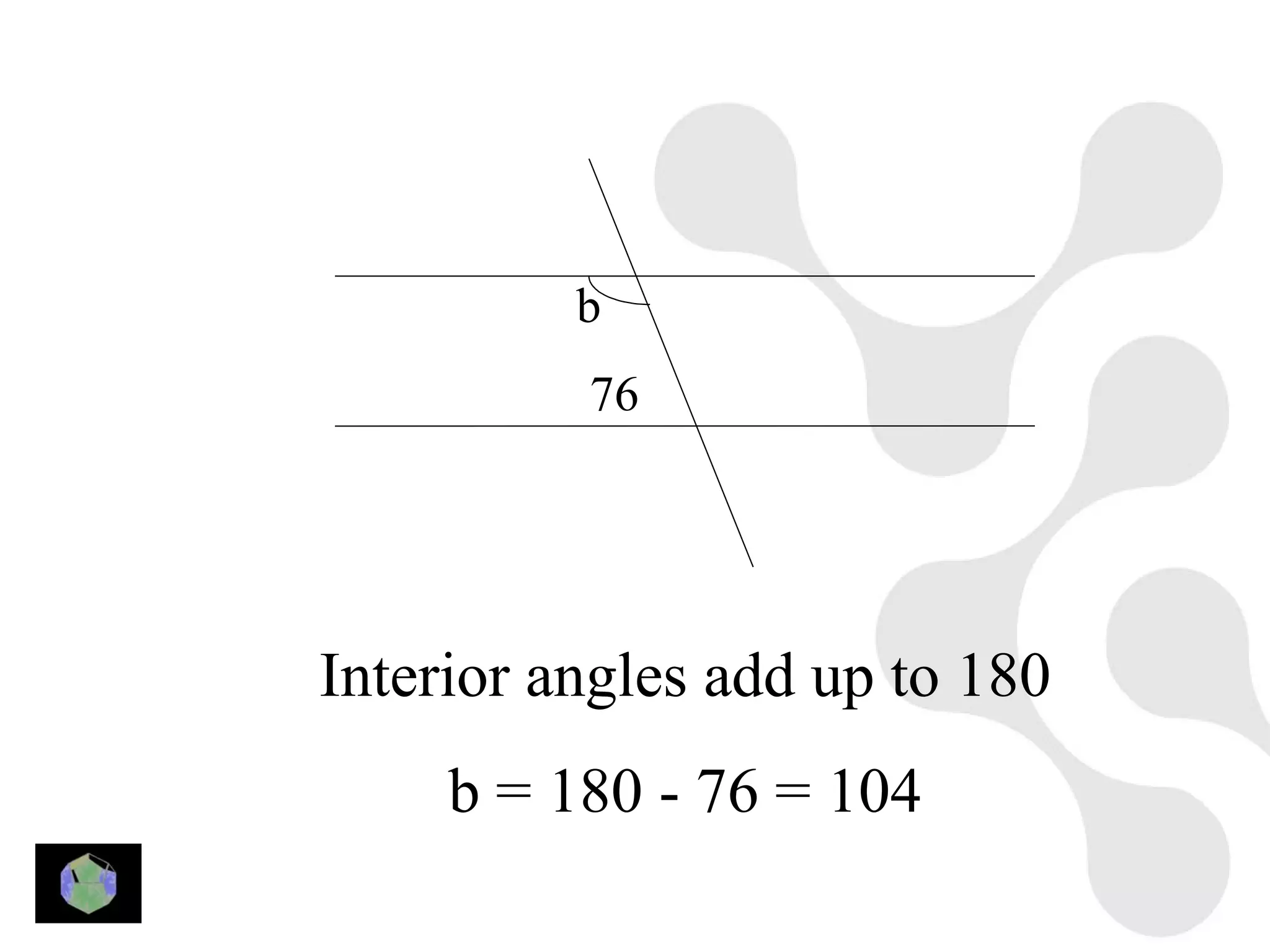
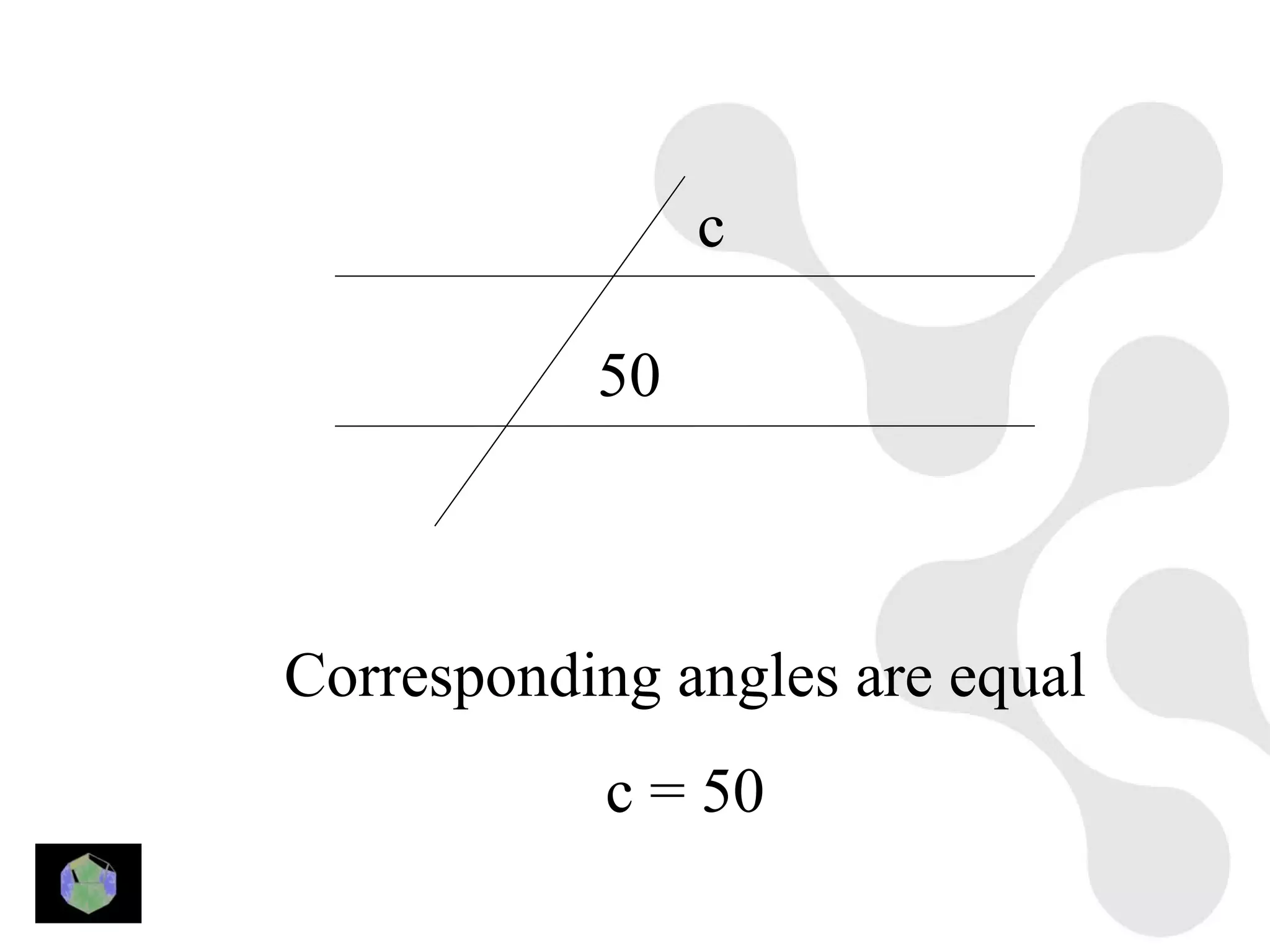
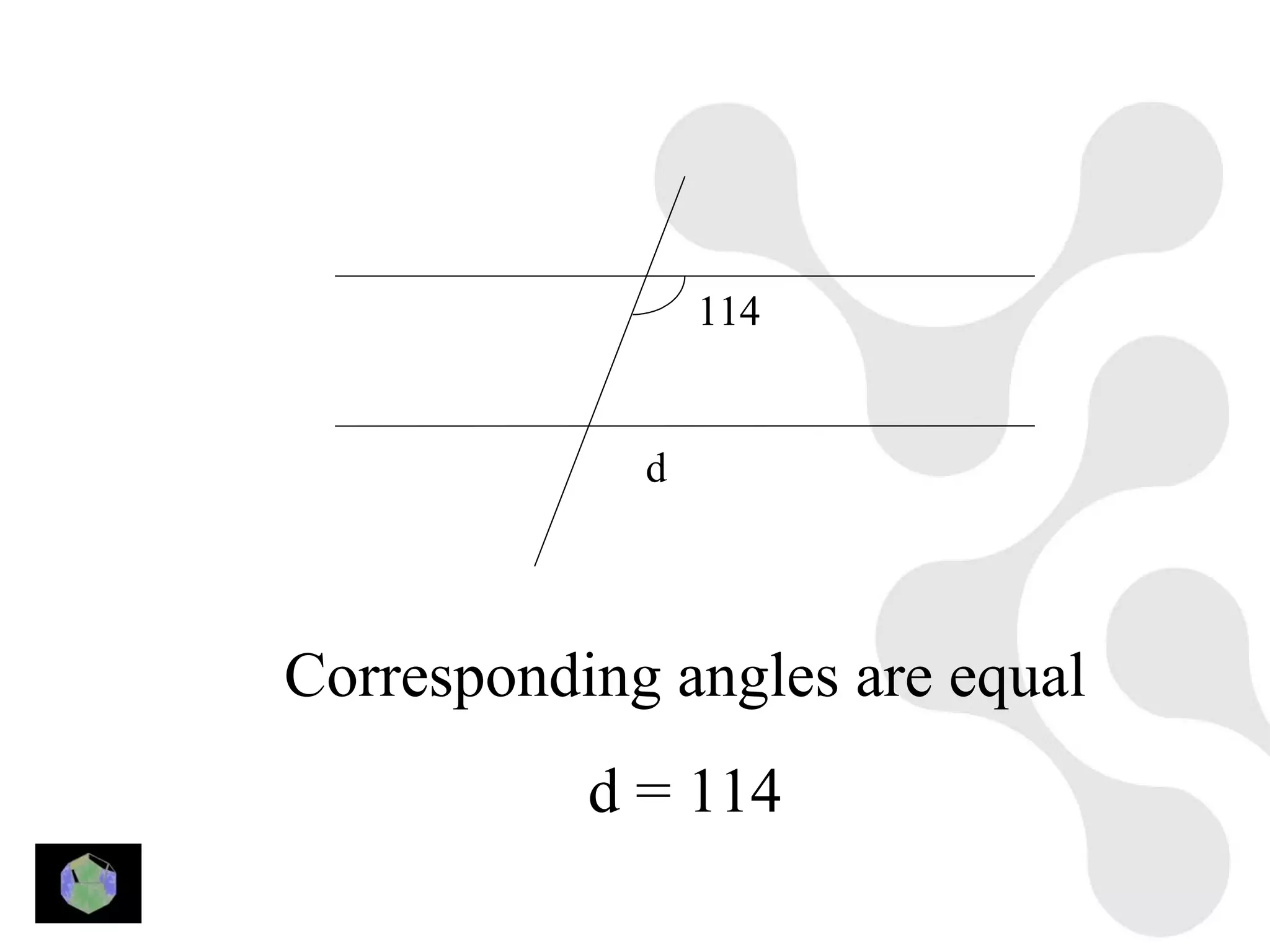
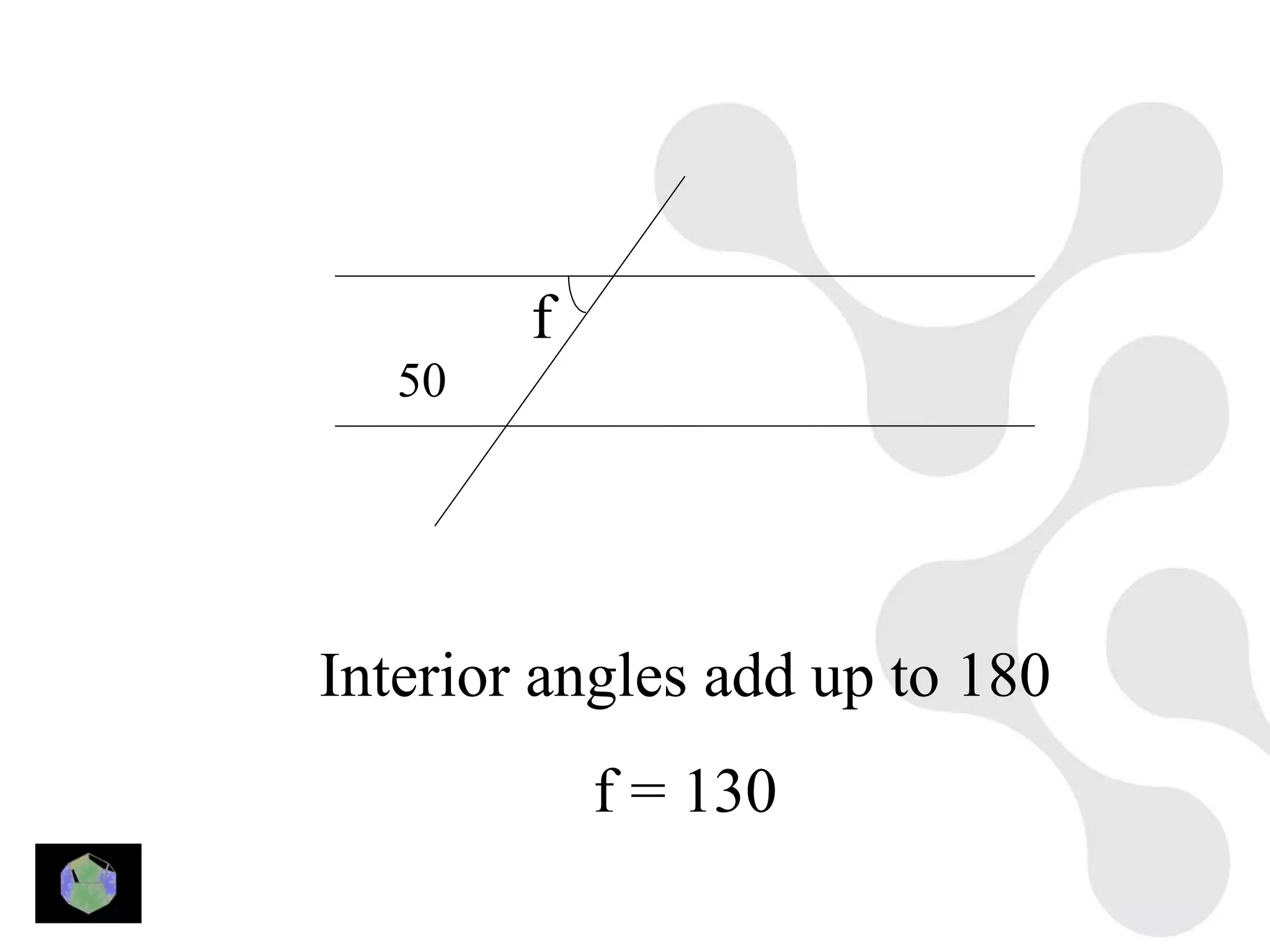
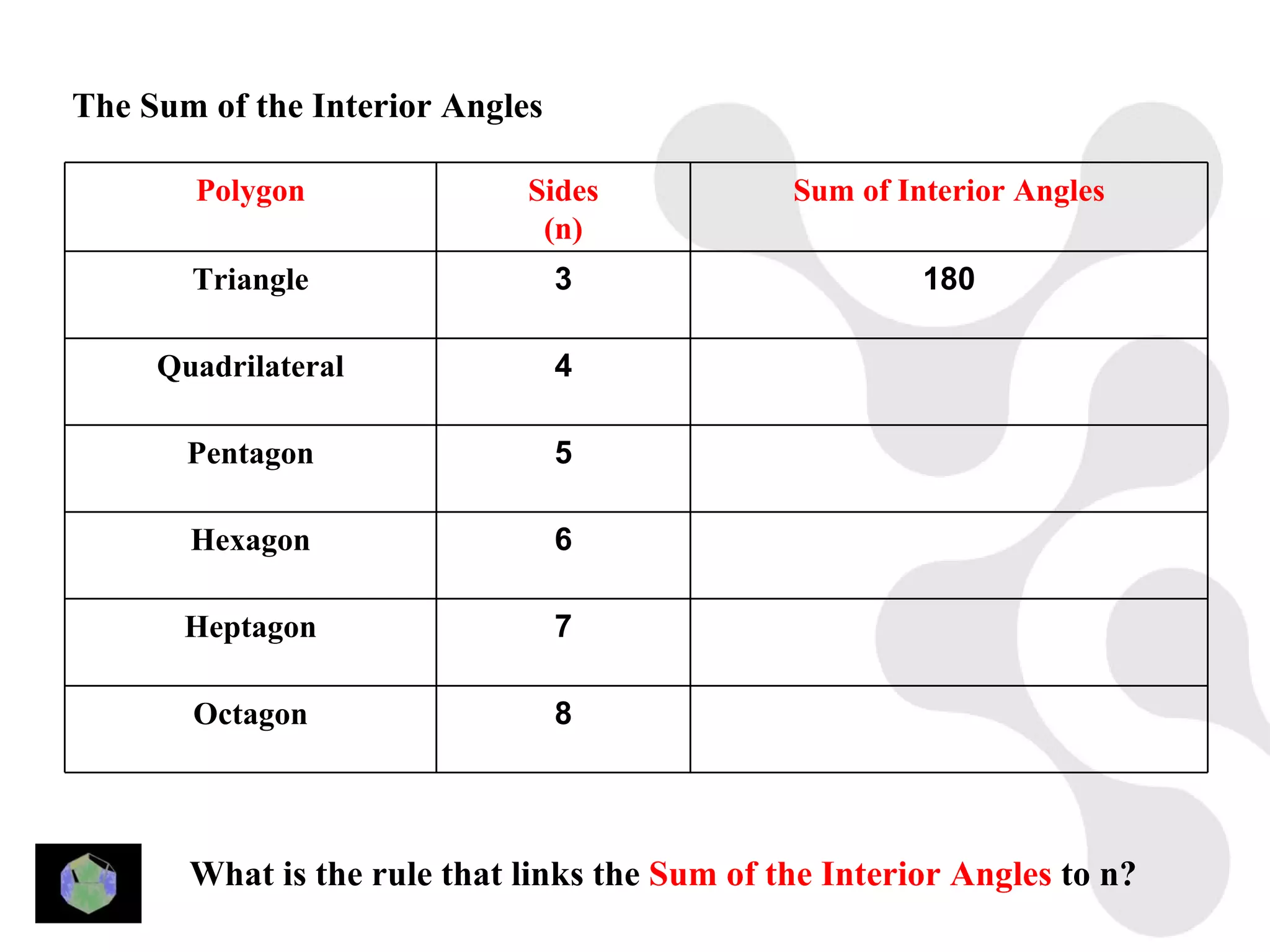
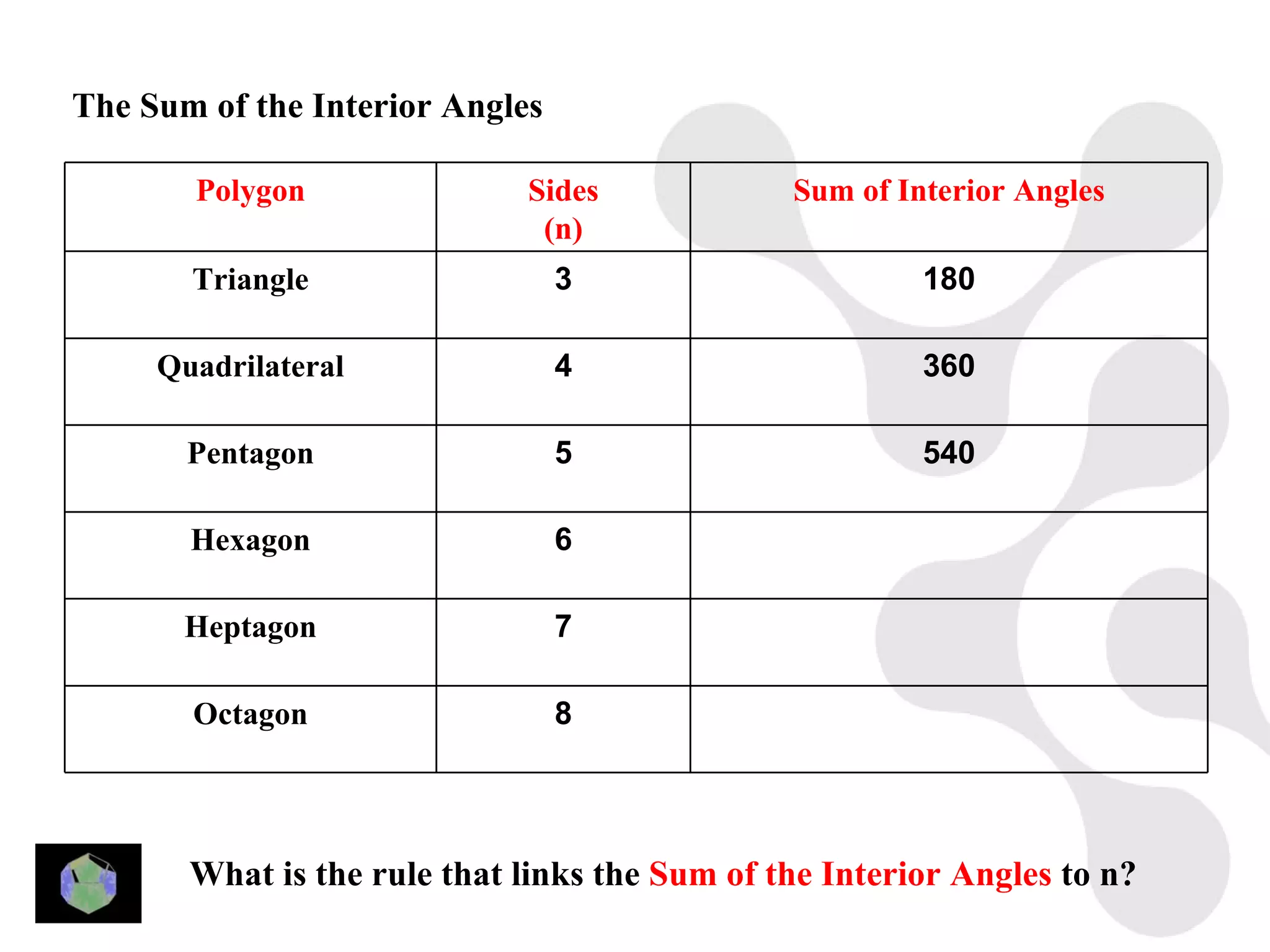
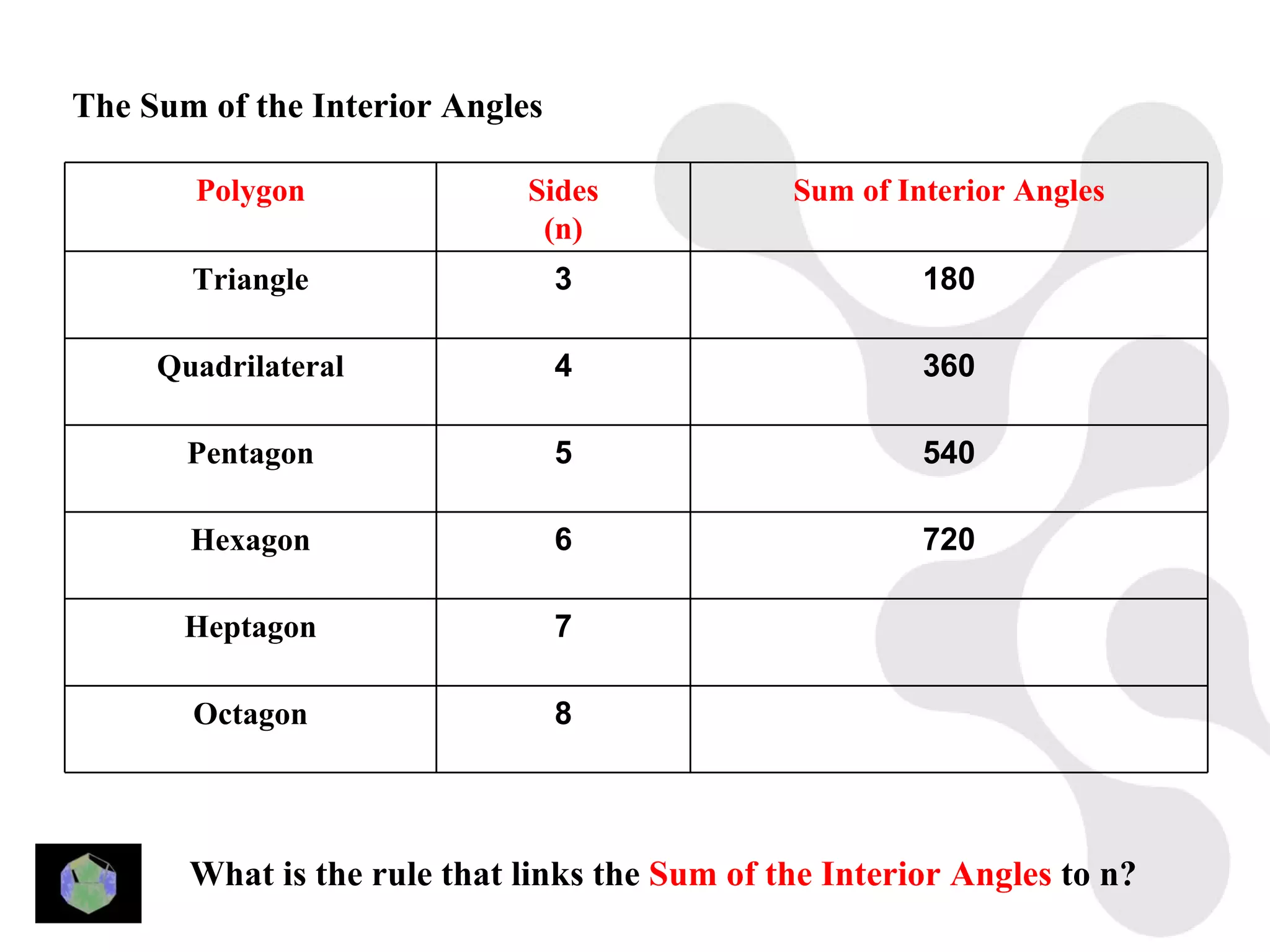
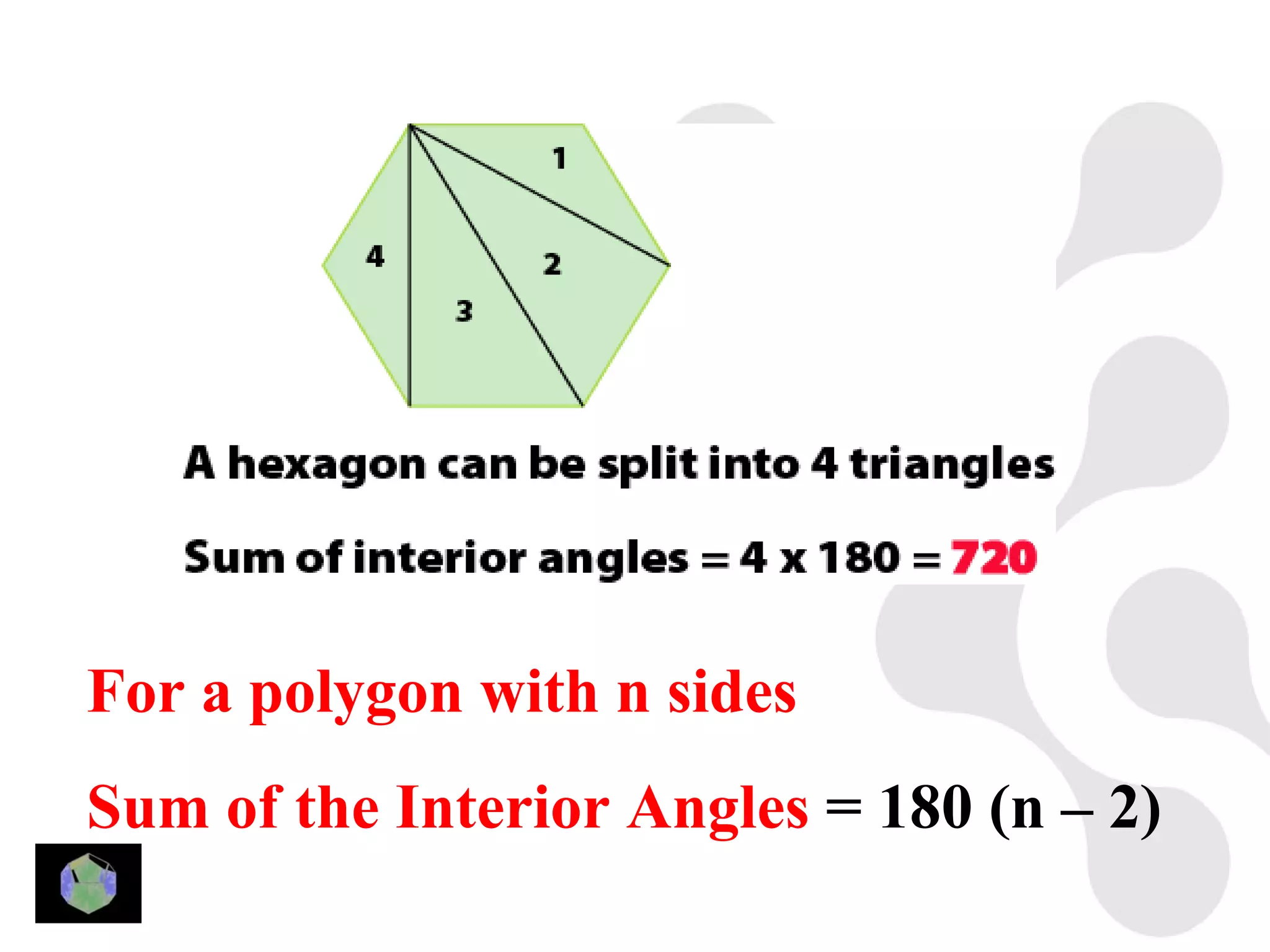
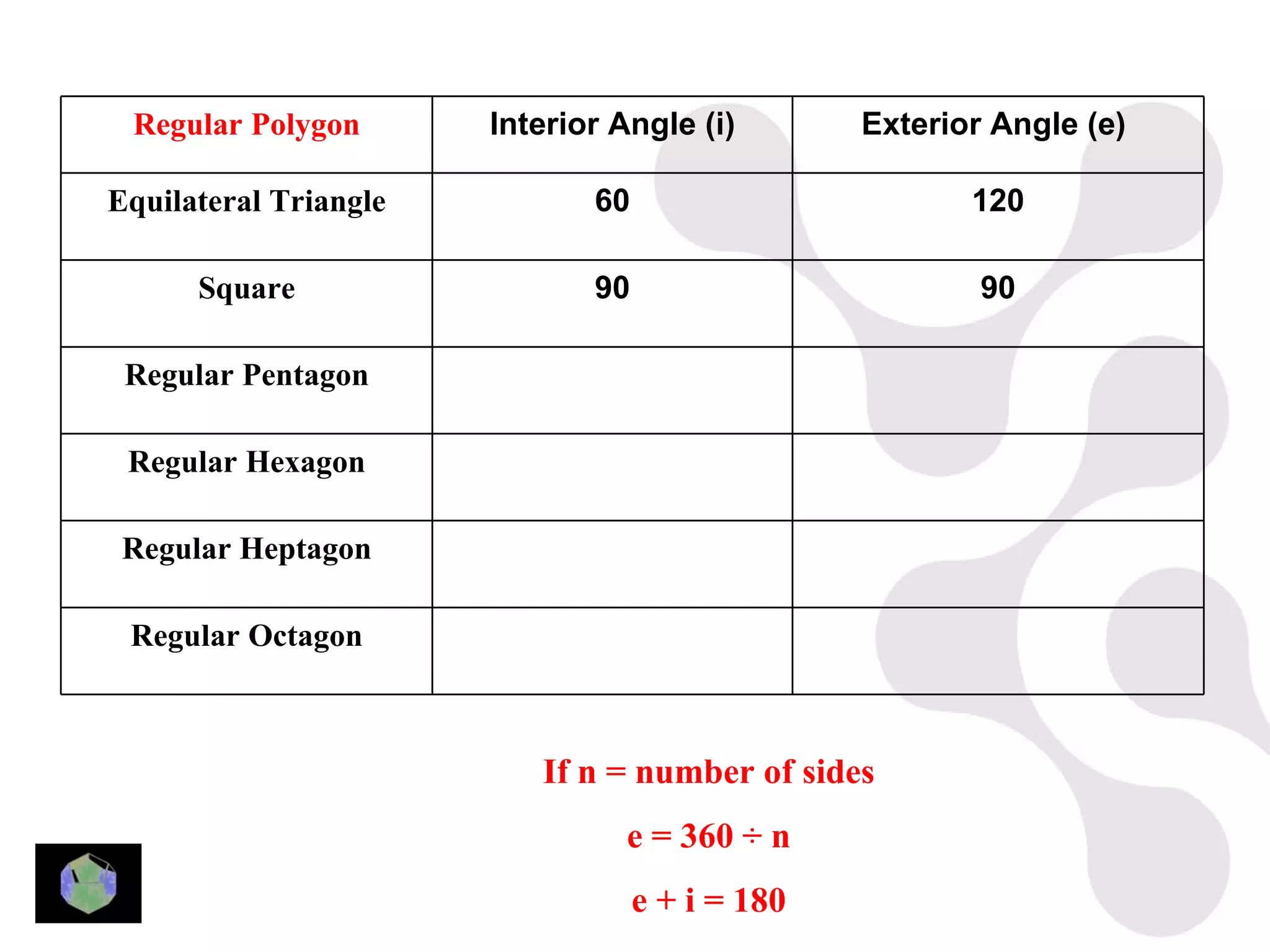
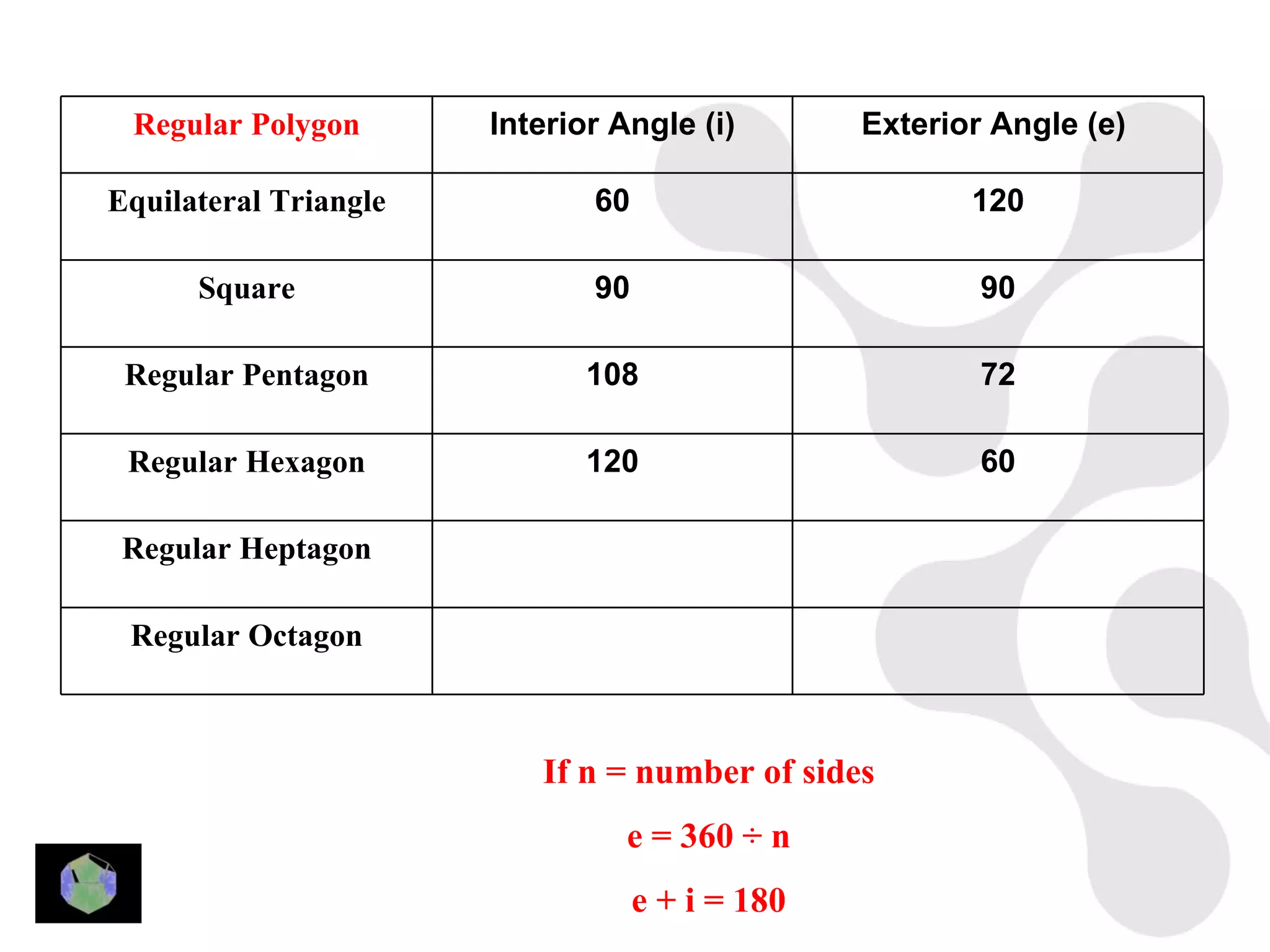
1) The document provides information about key stage 3 mathematics including solving equations using trial and improvement, percentages, ratios, sequences, straight line graphs, properties of shapes, and properties of polygons. 2) It gives examples of solving equations like x3 + x = 20 using guesses and checks to find the solution to the nearest tenth. 3) Properties of polygons are summarized, including the rule that the sum of the interior angles of an n-sided polygon is 180(n-2).

1. Key Stage 3
Mathematics
Key Facts
Level 6

2. Level 6
Number and Algebra

3. Solve the equation
x³ + x = 20
Using trial and improvement and give your answer to the nearest tenth
Guess Check Too Big/Too
Small/Correct

4. Solve the equation
x³ + x = 20
Using trial and improvement and give your answer to the nearest tenth
Guess Check Too Big/Too
Small/Correct
3 3³ + 3 = 30 Too Big

5. Solve the equation
x³ + x = 20
Using trial and improvement and give your answer to the nearest tenth
Guess Check Too Big/Too
Small/Correct
3 3³ + 3 = 30 Too Big
2 2³ + 2 = 10 Too Small

6. Solve the equation
x³ + x = 20
Using trial and improvement and give your answer to the nearest tenth
Guess Check Too Big/Too
Small/Correct
3 3³ + 3 = 30 Too Big
2 2³ + 2 = 10 Too Small
2.5 2.5³ + 2.5 =18.125 Too Small
2.6

7. Amounts as a %
• Fat in a mars bar 28g out of 35g. What percentage
is this?
Write as a fraction top ÷ bottom
converts a
fraction to a
• =28/35 decimal
Convert to a percentage (top ÷ bottom x 100)
• 28 ÷ 35 x 100 = 80% Multiply by 100
to make a
decimal into a
percentage

8. A percentage is a
fraction out of 100

11. The ratio of boys to girls in a class is 3:2
Altogether there are 30 students in the class.
How many boys are there?

12. The ratio of boys to girls in a class is 3:2
Altogether there are 30 students in the class.
How many boys are there?
The ratio 3:2 represents 5 parts (add 3 + 2)
Divide 30 students by the 5 parts (divide)
30 ÷ 5 = 6
Multiply the relevant part of the ratio by the
answer (multiply)
3 × 6 = 18 boys

14. A common multiple of 3 and
11 is 33, so change both
fractions to equivalent
fractions with a denominator
of 33
2 2 22 6
+ = +
3 11 33 33
28
=
33

15. A common multiple of 3 and 4
is 12, so change both fractions
to equivalent fractions with a
denominator of 12
2 1 8 3
- = -
3 4 12 12
5
=
12

16. Find the nth term of this sequence
7 14 21 28 35
6 13 20 27 34
7 7 7 7
Which times table is this pattern based on? 7
How does it compare to the 7 times table? Each number is 1 less
nth term = 7n - 1

17. Find the nth term of this sequence
9 18 27 36 45
6 15 24 33 42
9 9 9 9
Which times table is this pattern based on? 9
How does it compare to the 9 times table? Each number is 3 less
nth term = 9n - 3

19. - -

20. 4p + 5 = 75 - 3p
Swap Sides, Swap
Signs
4p + 5 = 75 - 3p
4p + = 75 -
7p = 70
p = 10

21. y axis
6 (3,6)
5
4 (2,4)
3
2 (1,2)
1
x axis
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1
-2
-3
-4
-5
(-3,-6) -6
The y coordinate is always double the x coordinate
y = 2x

22. Straight Line Graphs
y axis y = 4x
y = 3x
10
y = 5x y = 2x
8
6 y=x
4
2 y=½x
0
-4 -3 -2 -1 1 2 3 4 x axis
-2
-4
y = -x
-6
-8
-10

23. +6 1 x- 2
y axis 2x + 2 -5
10 y = 2x = 2x
y= y y=
8
6
4
2
0
-4 -3 -2 -1 1 2 3 4 x axis
-2
-4
-6
-8
-10

24. All straight line graphs can be expressed in the form
y = mx + c
m is the gradient of the line
and c is the y intercept
The graph y = 5x + 4 has gradient 5 and cuts the
y axis at 4

25. Level 6
Shape, Space and Measures

26. Cube Cuboid
Triangular Cylinder
Prism
Hexagonal Prism
Square
based Cone
Pyramid
Tetrahedron
Sphere

27. Using Isometric Paper
Which Cuboid is the odd one out?

30. a
50
Alternate angles are equal
a = 50

31. b
76
Interior angles add up to 180
b = 180 - 76 = 104

32. c
50
Corresponding angles are equal
c = 50

33. 114
d
Corresponding angles are equal
d = 114

34. e
112
Alternate angles are equal
e = 112

35. f
50
Interior angles add up to 180
f = 130

36. The Sum of the Interior Angles
Polygon Sides Sum of Interior Angles
(n)
Triangle 3 180
Quadrilateral 4
Pentagon 5
Hexagon 6
Heptagon 7
Octagon 8
What is the rule that links the Sum of the Interior Angles to n?

37. The Sum of the Interior Angles
Polygon Sides Sum of Interior Angles
(n)
Triangle 3 180
Quadrilateral 4 360
Pentagon 5
Hexagon 6
Heptagon 7
Octagon 8
What is the rule that links the Sum of the Interior Angles to n?

38. The Sum of the Interior Angles
Polygon Sides Sum of Interior Angles
(n)
Triangle 3 180
Quadrilateral 4 360
Pentagon 5 540
Hexagon 6
Heptagon 7
Octagon 8
What is the rule that links the Sum of the Interior Angles to n?

39. The Sum of the Interior Angles
Polygon Sides Sum of Interior Angles
(n)
Triangle 3 180
Quadrilateral 4 360
Pentagon 5 540
Hexagon 6 720
Heptagon 7
Octagon 8
What is the rule that links the Sum of the Interior Angles to n?

40. For a polygon with n sides
Sum of the Interior Angles = 180 (n – 2)

41. A regular polygon has equal sides and equal angles

42. Regular Polygon Interior Angle (i) Exterior Angle (e)
Equilateral Triangle 60 120
Square
Regular Pentagon
Regular Hexagon
Regular Heptagon
Regular Octagon
If n = number of sides
e = 360 ÷ n
e + i = 180

43. Regular Polygon Interior Angle (i) Exterior Angle (e)
Equilateral Triangle 60 120
Square 90 90
Regular Pentagon
Regular Hexagon
Regular Heptagon
Regular Octagon
If n = number of sides
e = 360 ÷ n
e + i = 180

44. Regular Polygon Interior Angle (i) Exterior Angle (e)
Equilateral Triangle 60 120
Square 90 90
Regular Pentagon 108 72
Regular Hexagon
Regular Heptagon
Regular Octagon
If n = number of sides
e = 360 ÷ n
e + i = 180

45. Regular Polygon Interior Angle (i) Exterior Angle (e)
Equilateral Triangle 60 120
Square 90 90
Regular Pentagon 108 72
Regular Hexagon 120 60
Regular Heptagon
Regular Octagon
If n = number of sides
e = 360 ÷ n
e + i = 180

47. Translate the object by
()
4
-3

48. Translate the object by
()
4
-3
Move each
corner of the
object 4 squares
across and 3
squares down
Image

49. Rotate by 90 degrees anti-clockwise about c
C

50. Rotate by 90 degrees anti-clockwise about C
Image
C
Remember to ask for tracing paper

51. We divide by 2 because the area of the
triangle is half that of the rectangle that Triangle
surrounds it Area = base × height ÷ 2
h
A = bh/2
b
Parallelogram
Area = base × height
h
A = bh
b
a Trapezium
h
A = ½ h(a + b)
b
The formula for the trapezium is given in
the front of the SATs paper

52. The circumference
of a circle is the
distance around the
outside
diameter
Circumference = π × diameter
Where π = 3.14 (rounded to 2 decimal places)

53. The radius of a circle is
30m. What is the
circumference?
r=30, d=60
r = 30
C= πd d = 60
C = 3.14 × 60
C = 18.84 m

54. Circle Area = πr2

55. π = 3. 141 592 653 589 793 238 462 643
Circumference = π × 20 Need radius = distance
= 3.142 × 20 from the centre of a
= 62.84 cm circle to the edge
10cm
πd πr²
10cm
The distance around
Area = π × 100
the outside of a circle
= 3.142 × 100
= 314.2 cm²
Need diameter = distance
across the middle of a circle

56. Volume of a cuboid
V= length × width × height
10 cm
4 cm 9 cm

57. Volume of a cuboid
V= length × width × height
V= 9 × 4 × 10 10 cm
= 360 cm³
4 cm 9 cm

60. Level 6
Data Handling

61. Draw a Pie Chart to show the information in the table below
Colour Frequency
Blue 5
Green 3
Yellow 2
Purple 2
Pink 4
Orange 1
Red 3
A pie chart to show the favourite colour in our class

62. Draw a Pie Chart to show the information in the table below
Colour Frequency
Blue 5
Green 3
Yellow 2
Purple 2
Pink 4
Orange 1
Red 3
TOTAL 20
Add the frequencies to
find the total
A pie chart to show the favourite colour in our class

63. Draw a Pie Chart to show the information in the table below
Colour Frequency
Blue 5
Green 3
Yellow 2
Purple 2
Pink 4
Orange 1 DIVIDE 360° by
Red 3 the total to find the
TOTAL 20 angle for 1 person
360 ÷ 20 = 18
Add the frequencies to
find the total
A pie chart to show the favourite colour in our class

64. Draw a Pie Chart to show the information in the table below
Colour Frequency Angle
Blue 5 5 × 18 = 90 Multiply each frequency by the angle
Green 3 3 × 18 = 54
for 1 person
Yellow 2 2 × 18 = 36
Purple 2 2 × 18 = 36
Pink 4 4 × 18 = 72
Orange 1 1 × 18 = 18 DIVIDE 360° by
Red 3 3 × 18 = 54 the total to find the
TOTAL 20 angle for 1 person
360 ÷ 20 = 18
Add the frequencies to
find the total
A pie chart to show the favourite colour in our class

65. Draw a Pie Chart to show the information in the table below
Colour Frequency Angle
Blue 5 5 × 18 = 90
A bar chart to show the favourite colour in our class
Green 3 3 × 18 = 54
Yellow 2 2 × 18 = 36 Red
Blue
Purple 2 2 × 18 = 36
Orange
Pink 4 4 × 18 = 72
Orange 1 1 × 18 = 18
Pink
Green
Red 3 3 × 18 = 54
TOTAL 20 Purple Yellow

66. Length of Frequency
Draw a frequency polygon to show string
the information in the table 0 < x ≤ 20 10
20 < x ≤ 40 20
40 < x ≤ 60 45
60 < x ≤ 80 32
80 < x ≤ 100 0

67. Length of Frequency
Draw a frequency polygon to show string (x)
the information in the table 0 < x ≤ 20 10
20 < x ≤ 40 20
40 < x ≤ 60 45
60 < x ≤ 80 32
Plot the point using the 80 < x ≤ 100 0
midpoint of the interval
50 frequency
f
40
30
20
10
Use a continuous scale
for the x-axis x
10 20 30 40 50 60 70 80 90 100

68. Length of Frequency
Draw a histogram to show string
the information in the table 0 < x ≤ 20 10
20 < x ≤ 40 20
40 < x ≤ 60 45
60 < x ≤ 80 32
80 < x ≤ 100 0

69. Length of Frequency
Draw a histogram to show string (x)
the information in the table 0 < x ≤ 20 10
20 < x ≤ 40 20
40 < x ≤ 60 45
60 < x ≤ 80 32
80 < x ≤ 100 0
50 frequency
f
40
30
20
10
Use a continuous scale
for the x-axis x
10 20 30 40 50 60 70 80 90 100

70. Describe the correlation between the marks scored in test A and test B
A Scatter Diagram to compare the marks of students in 2 maths tests
140
120
100
80
Test B
60
40
20
0
0 20 40 60 80 100 120 140
Test A

71. Describe the correlation between the marks scored in test A and test B
A Scatter Diagram to compare the marks of students in 2 maths tests
160
140
120
100
Test B
80
The correlation is
positive because as
60
40
marks in test A
increase so do the
20
marks in test B
0
0 20 40 60 80 100 120 140 160
Test A

72. y Negative Correlation
12
10
8
6
4
2
x
0
0 2 4 6 8 10 12

73. The sample or probability space shows all 36 outcomes
when you add two normal dice together.
Total Probability
1 1
/36
Dice 1
2
1 2 3 4 5 6 3
4
1 2 3 4 5 6 7
5 4
/36
2 3 4 5 6 7 8 6
7
3 4 5 6 7 8 9
Dice 2 8
4 5 6 7 8 9 10 9
5 6 7 8 9 10 11 10
11
6 7 8 9 10 11 12 12

74. The sample space shows all 36 outcomes when you find the
difference between the scores of two normal dice.
Dice 1
Total Probability
1 2 3 4 5 6
0
1 0 1 2 3 4 5
1 10
/36
2 1 0 1 2 3 4
2
3 2 1 0 1 2 3 3
Dice 2
4 3 2 1 0 1 2 4 4
/36
5 4 3 2 1 0 1 5
6 5 4 3 2 1 0

75. The total probability of all the mutually exclusive outcomes of
an experiment is 1
A bag contains 3 colours of beads, red, white and blue.
The probability of picking a red bead is 0.14
The probability of picking a white bead is 0.2
What is the probability of picking a blue bead?

76. The total probability of all the mutually exclusive outcomes of
an experiment is 1
A bag contains 3 colours of beads, red, white and blue.
The probability of picking a red bead is 0.14
The probability of picking a white bead is 0.2
What is the probability of picking a blue bead?
0.14 + 0.2 = 0.34
1 - 0.34 = 0.66

77. © Dave Cavill