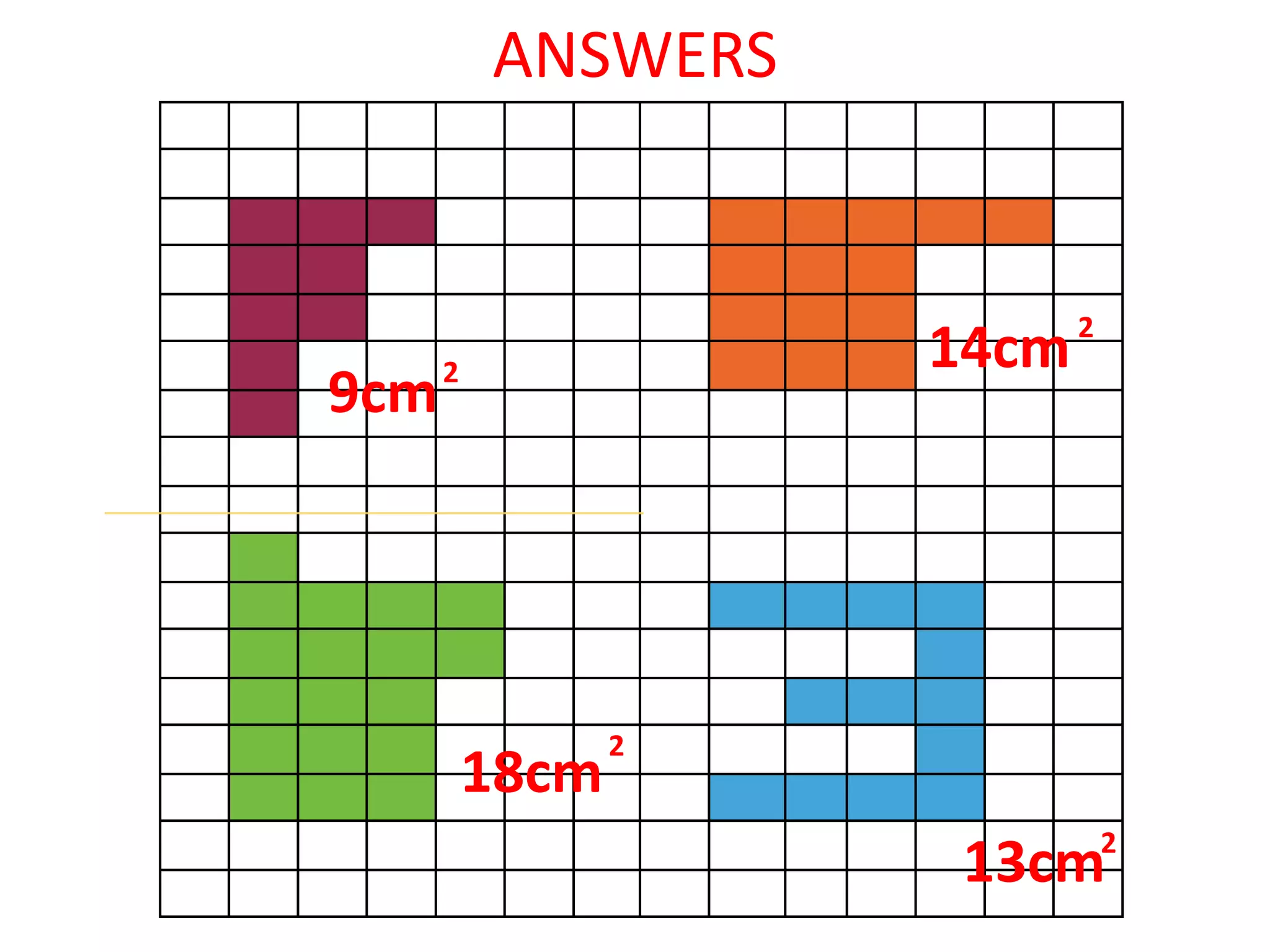
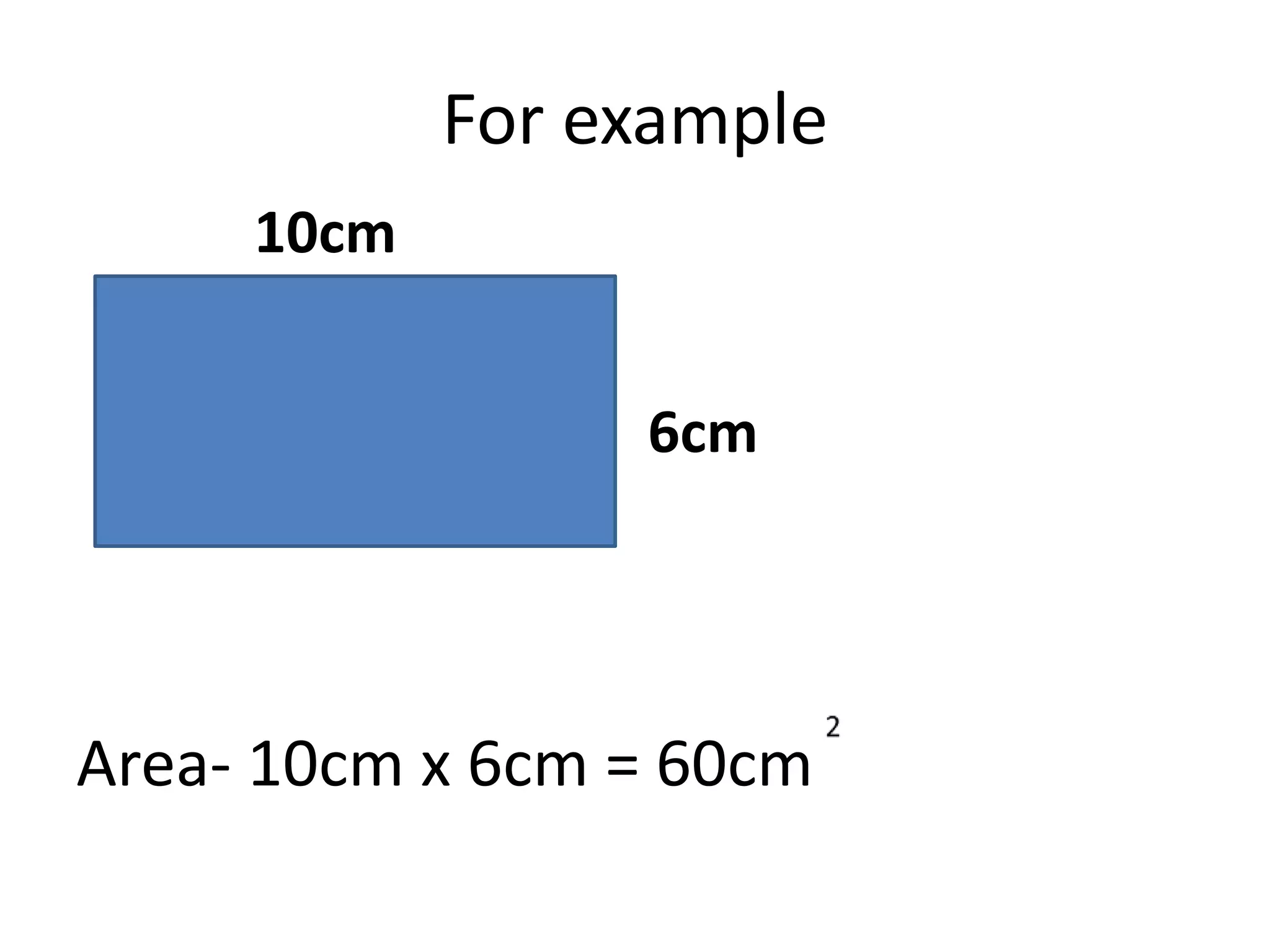
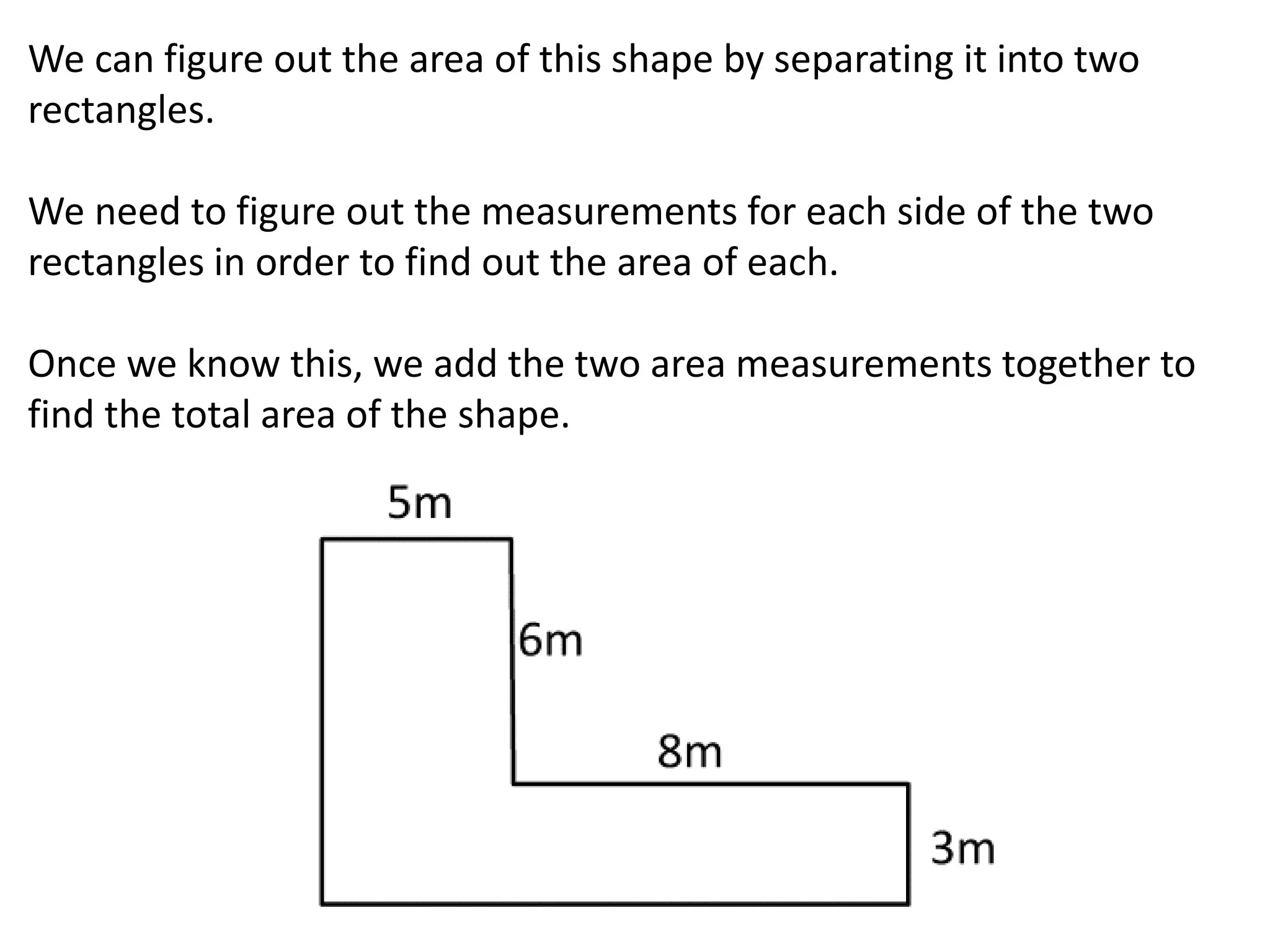
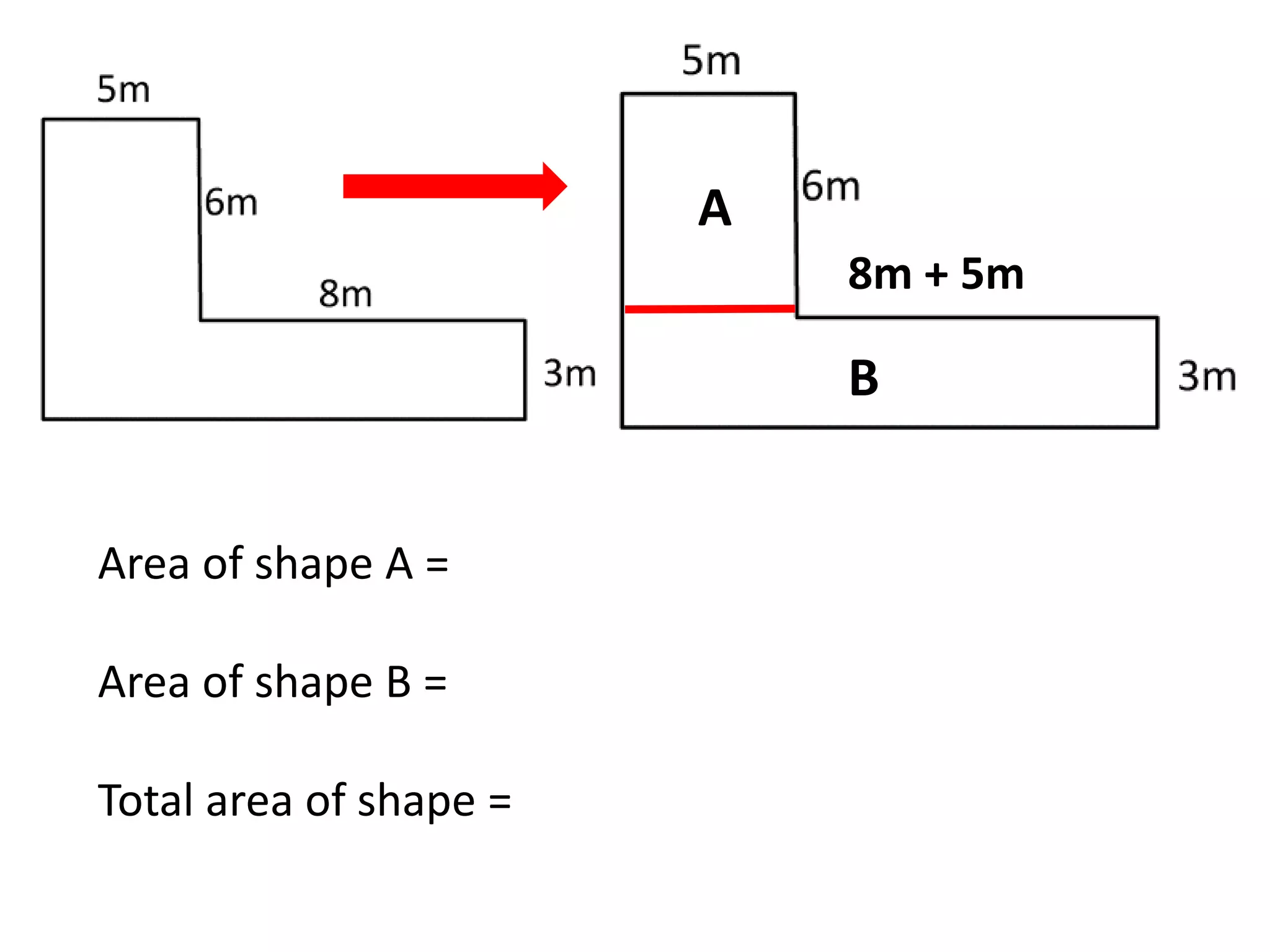
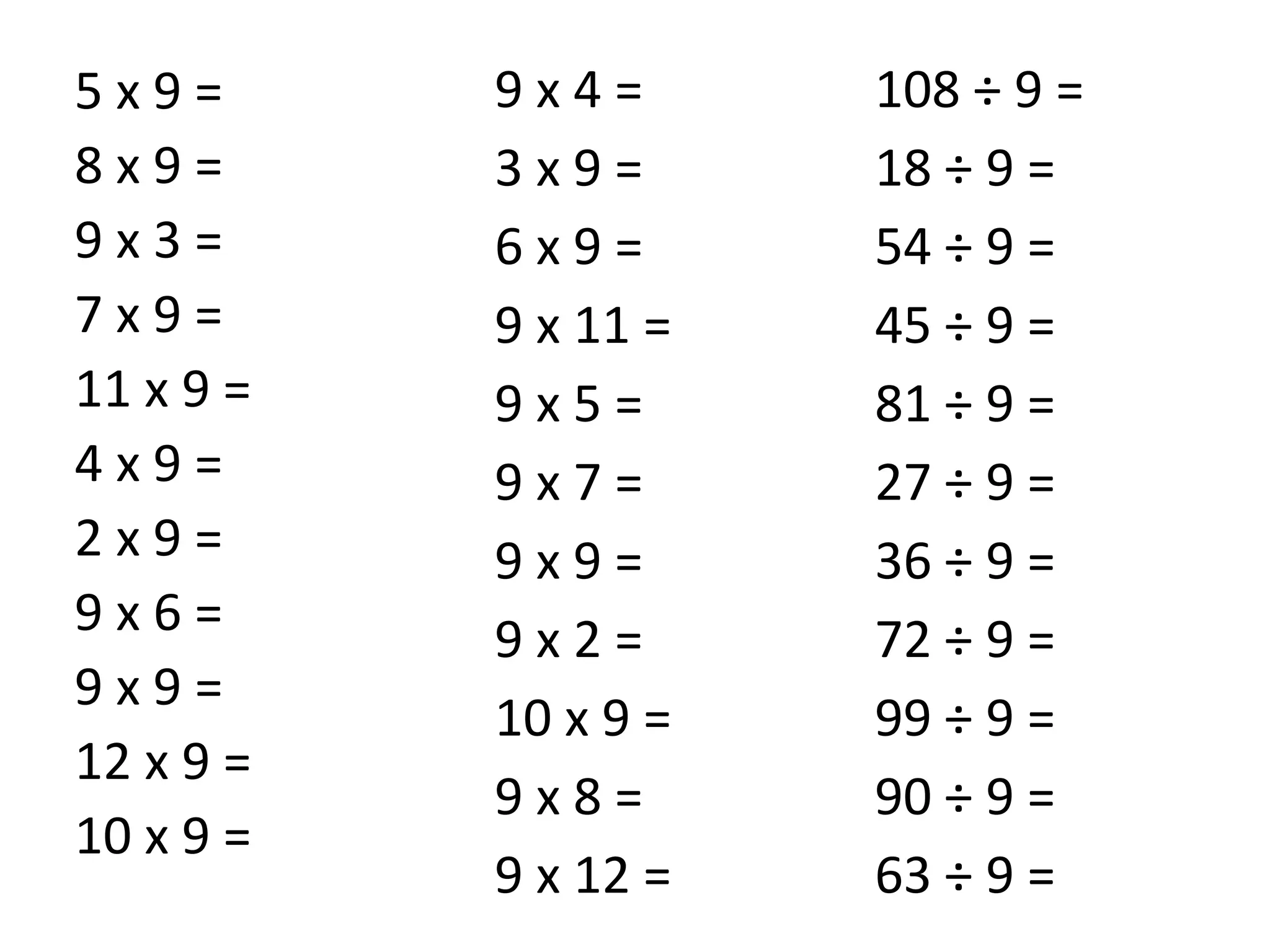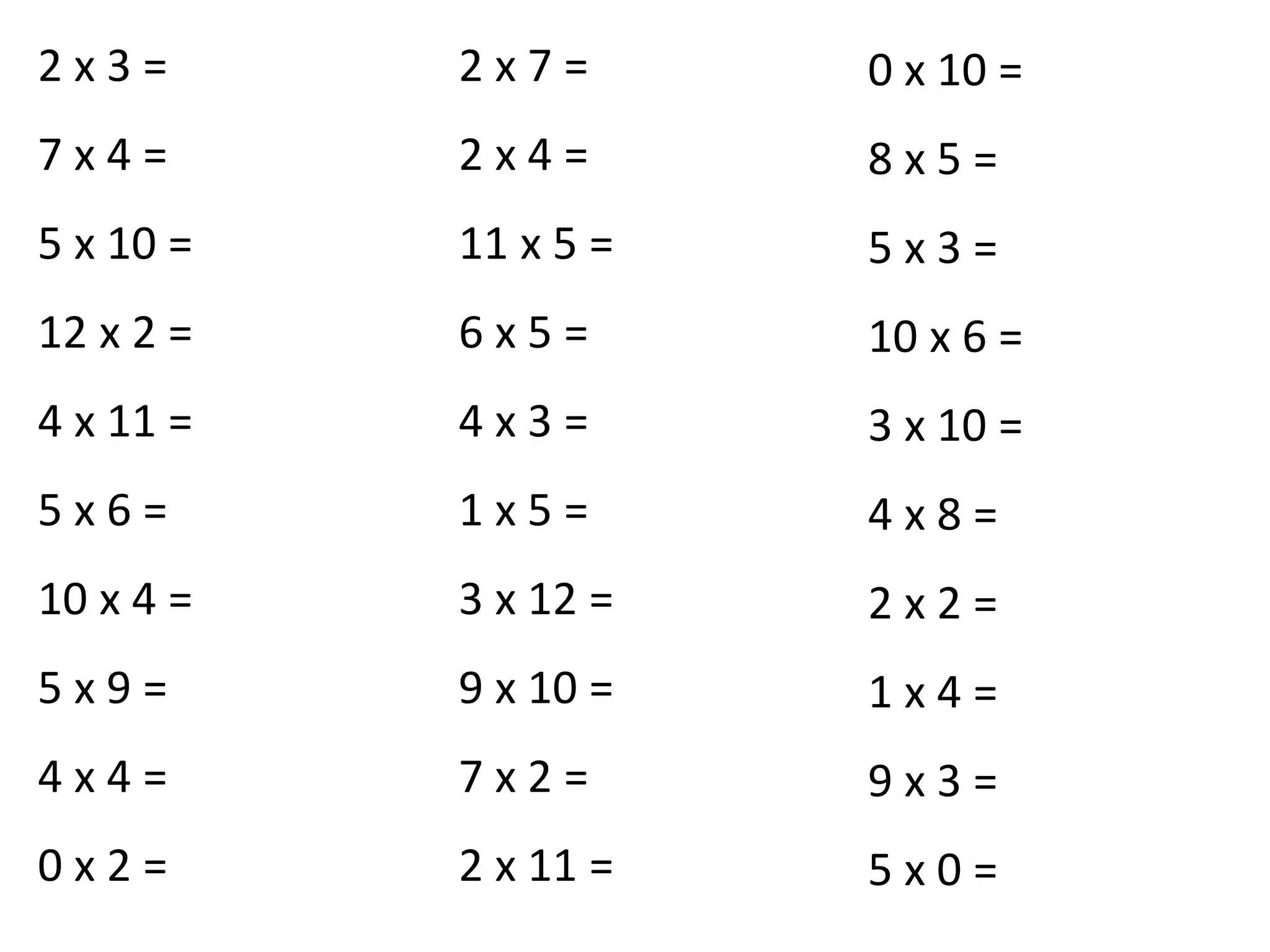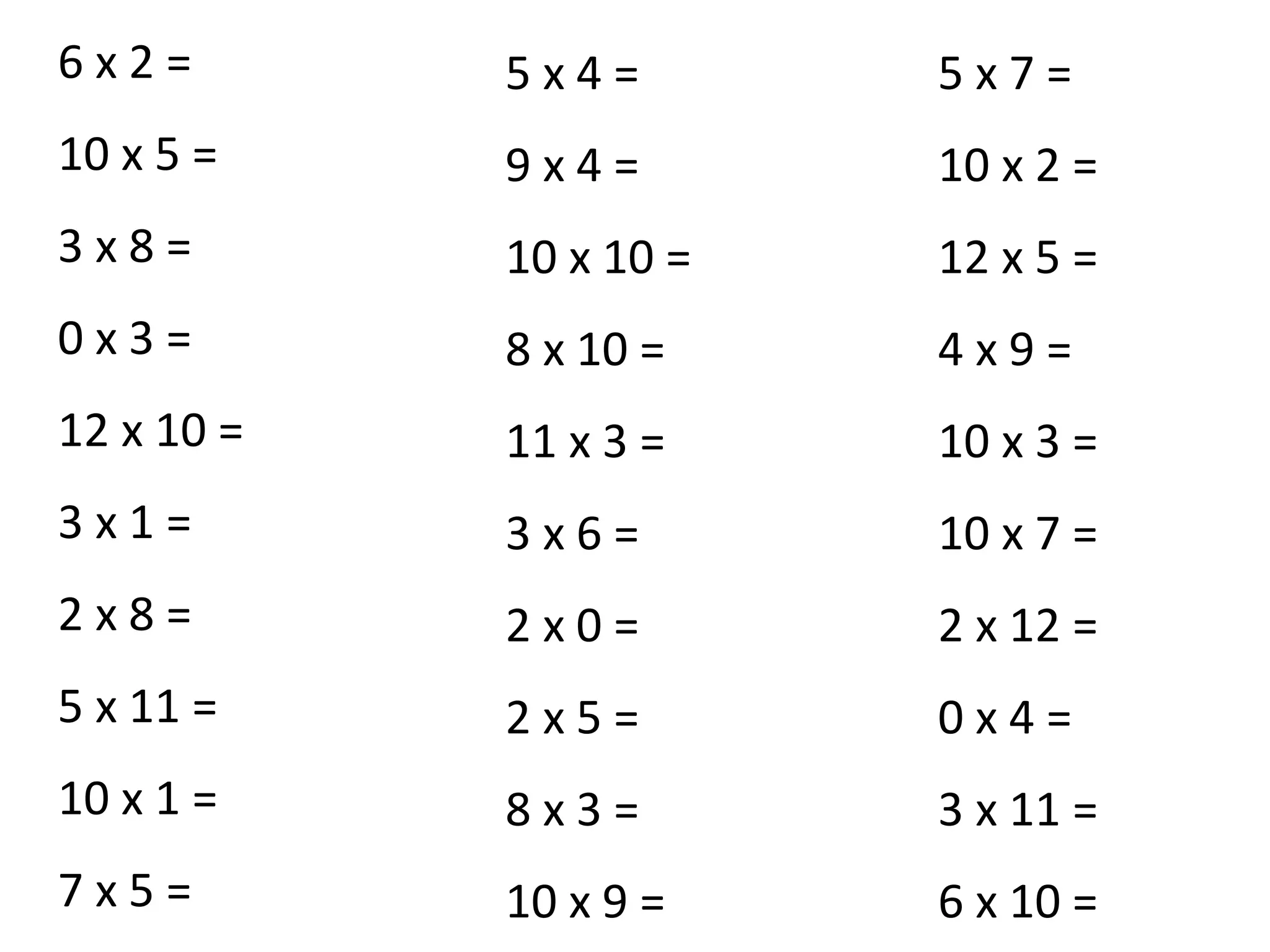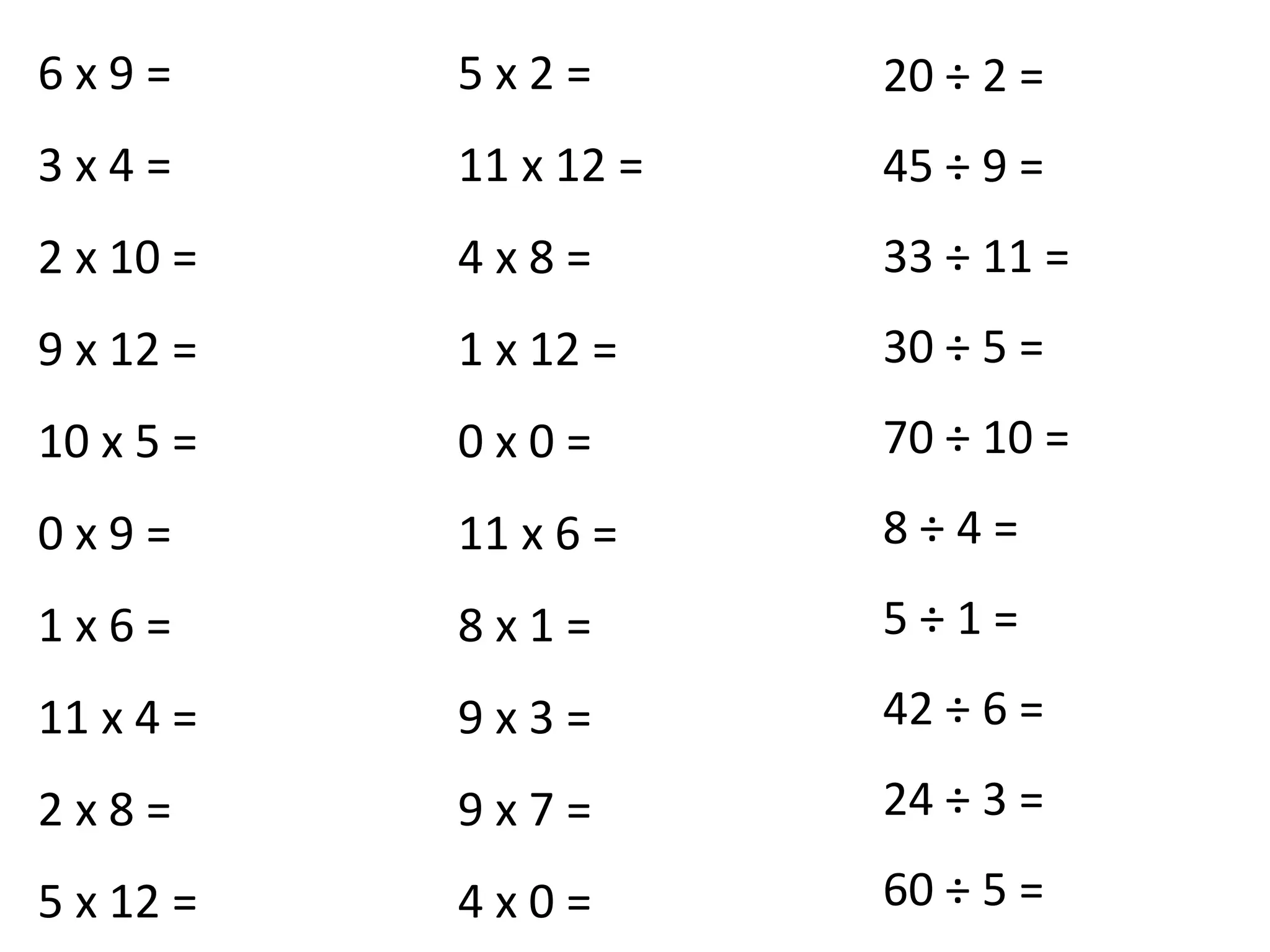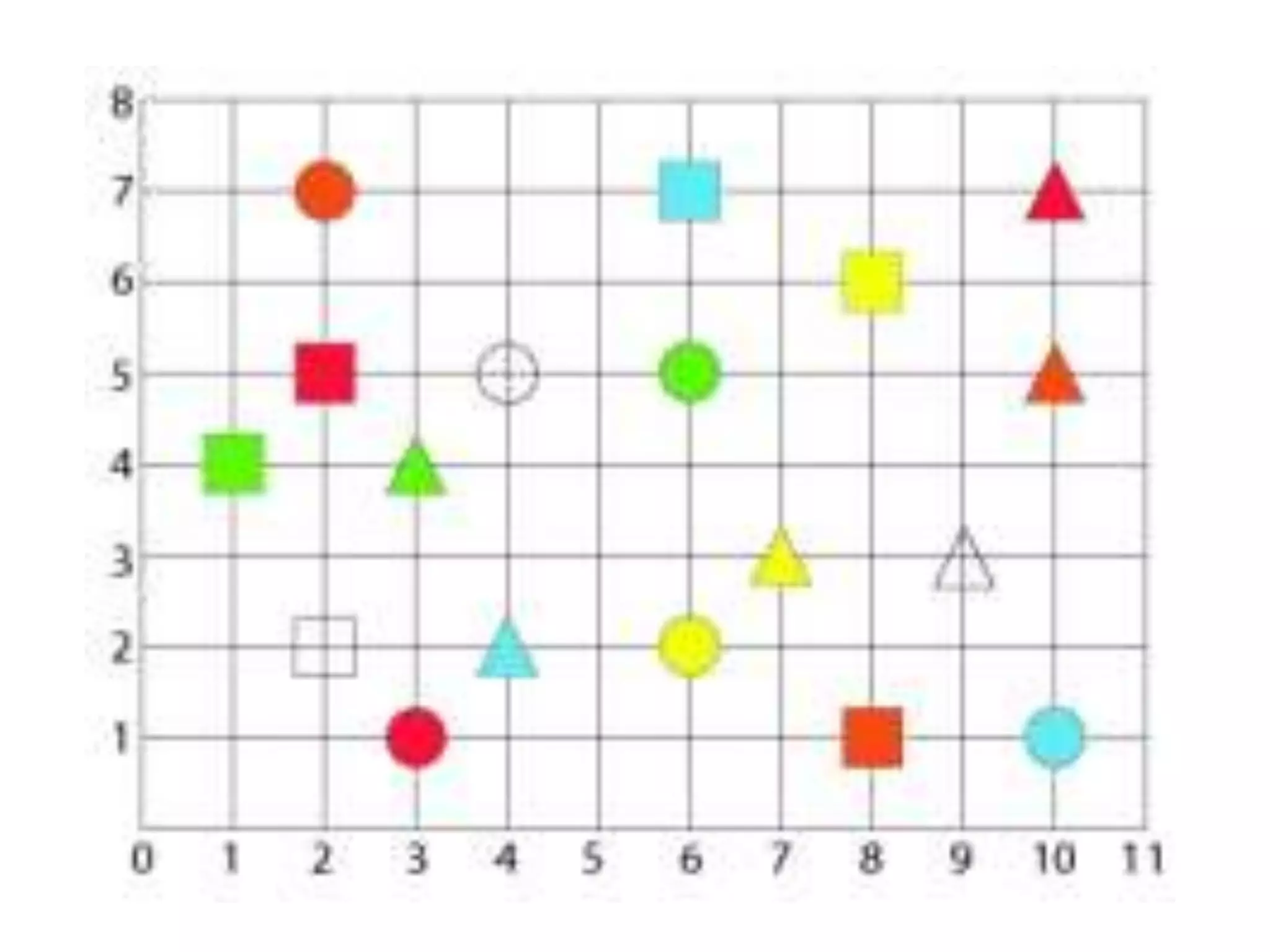
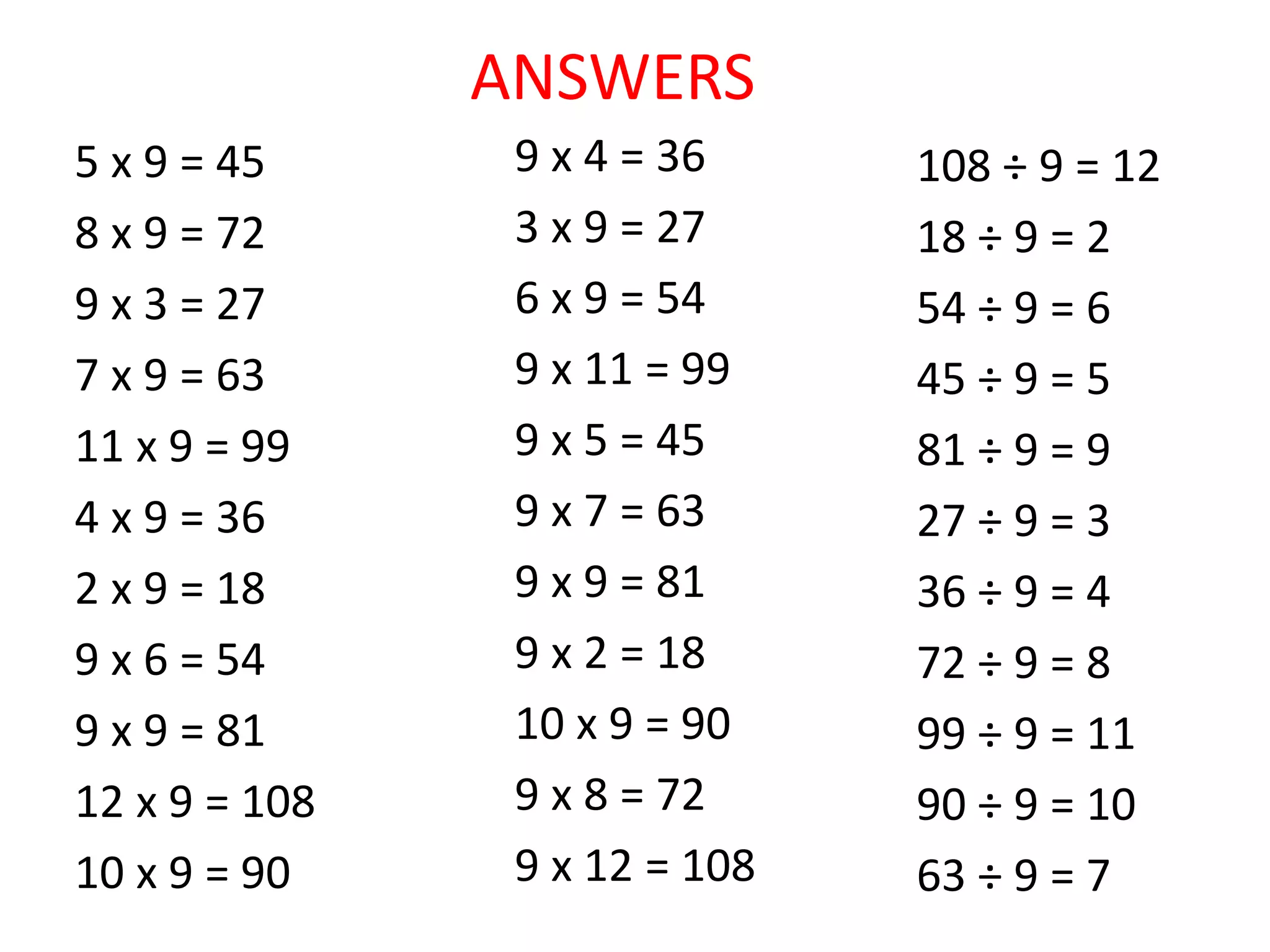
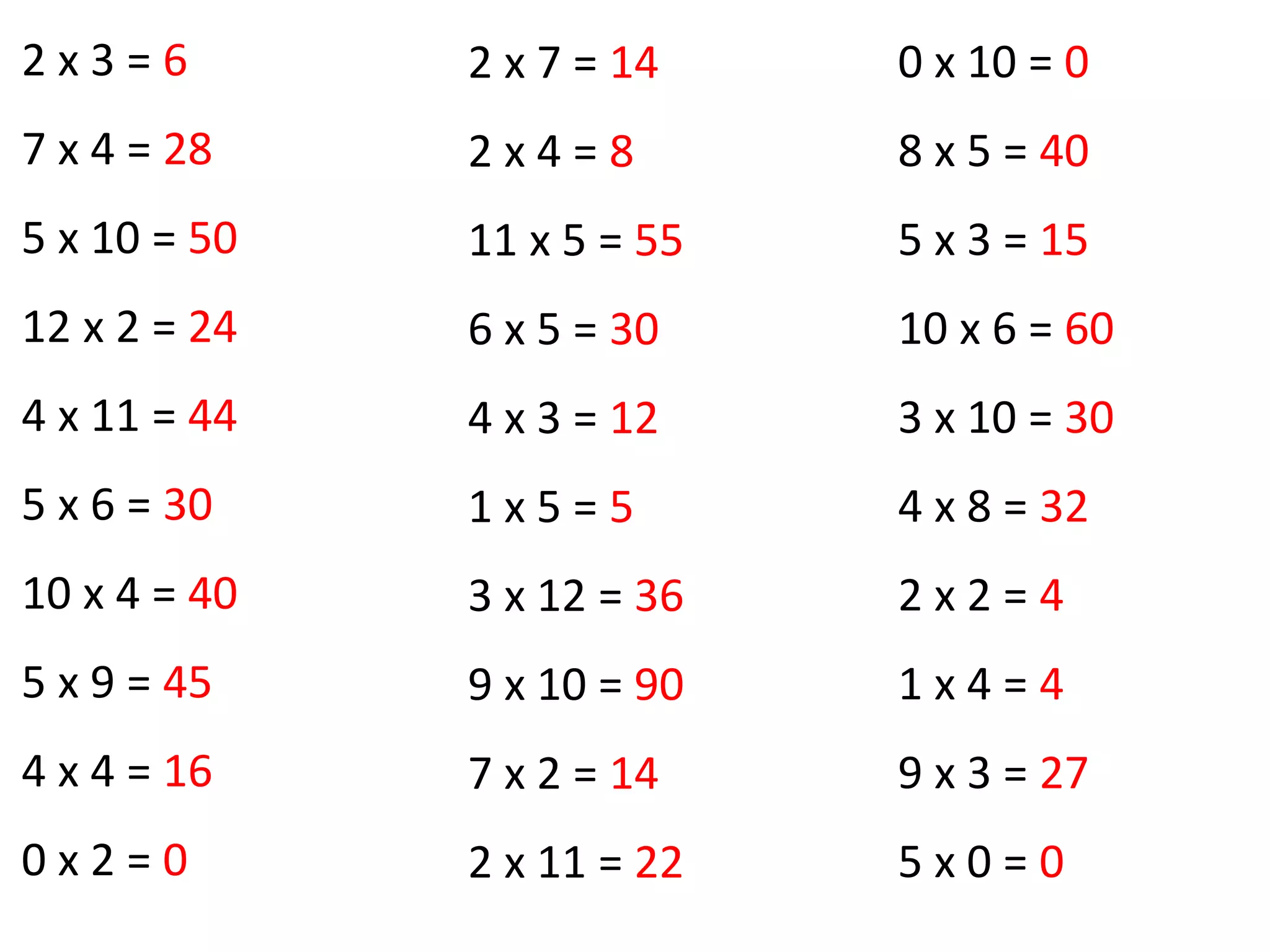
The document contains a teacher's notes and examples for teaching students about coordinates, inverse operations, and bus stop division. For coordinates, it provides examples of writing the coordinates of objects on a graph, naming shapes at given coordinates, and an extra challenge involving matching a shape's x and y coordinates. For inverse operations, it explains that multiplication and division are inverse operations, and examples are given to show using known calculations to derive the other three related calculations. 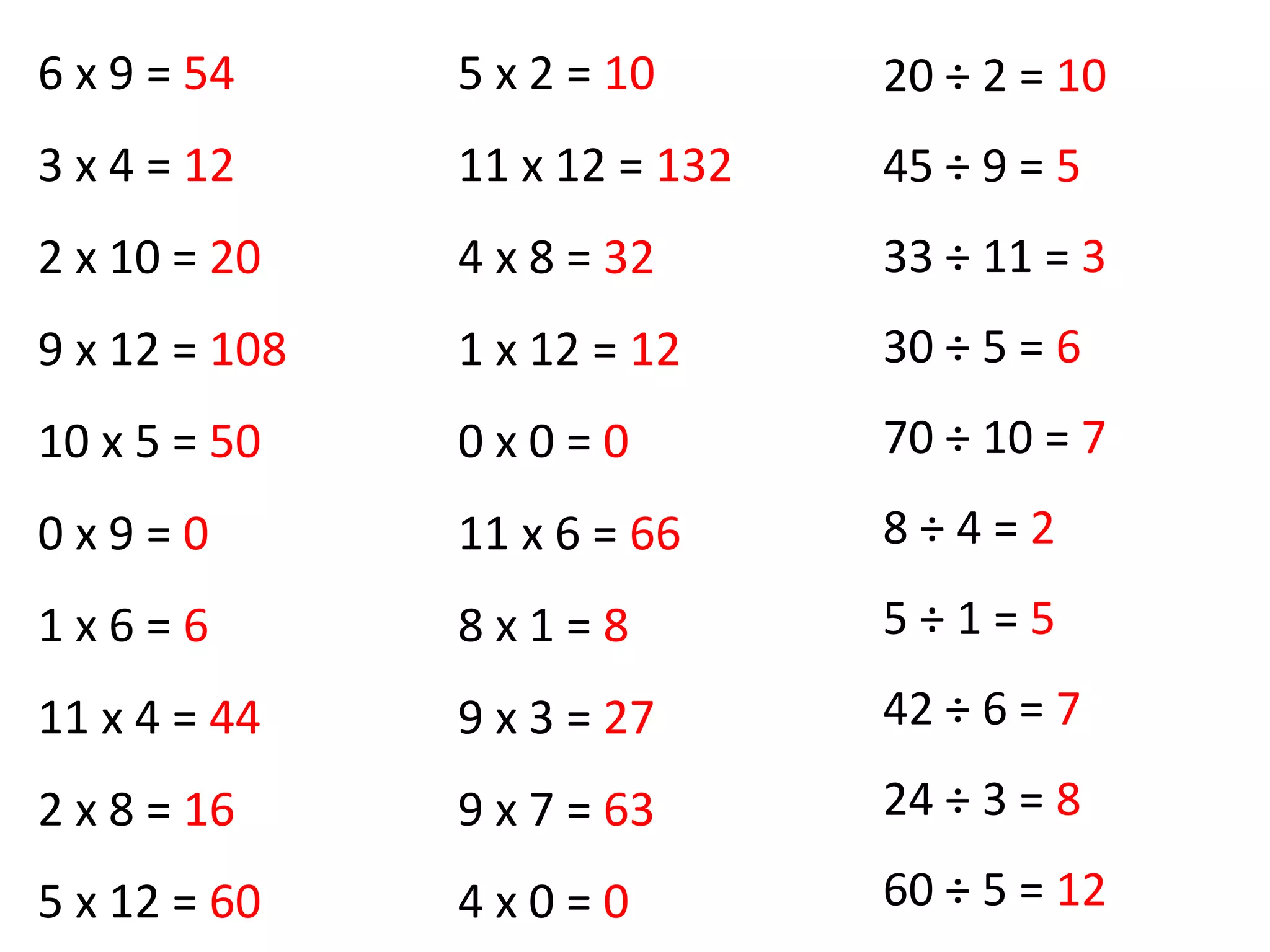For bus stop division, it provides multiplication examples to practice the concept. A video link is included to remind students how to use the bus stop method for long division. Further practice examples using bus stop division are listed but not shown.

1. 04/05/20
WALT: read and write co-ordinates

2. 5 x 9 =
8 x 9 =
9 x 3 =
7 x 9 =
11 x 9 =
4 x 9 =
2 x 9 =
9 x 6 =
9 x 9 =
12 x 9 =
10 x 9 =
9 x 4 =
3 x 9 =
6 x 9 =
9 x 11 =
9 x 5 =
9 x 7 =
9 x 9 =
9 x 2 =
10 x 9 =
9 x 8 =
9 x 12 =
108 ÷ 9 =
18 ÷ 9 =
54 ÷ 9 =
45 ÷ 9 =
81 ÷ 9 =
27 ÷ 9 =
36 ÷ 9 =
72 ÷ 9 =
99 ÷ 9 =
90 ÷ 9 =
63 ÷ 9 =

3. ANSWERS
5 x 9 = 45
8 x 9 = 72
9 x 3 = 27
7 x 9 = 63
11 x 9 = 99
4 x 9 = 36
2 x 9 = 18
9 x 6 = 54
9 x 9 = 81
12 x 9 = 108
10 x 9 = 90
9 x 4 = 36
3 x 9 = 27
6 x 9 = 54
9 x 11 = 99
9 x 5 = 45
9 x 7 = 63
9 x 9 = 81
9 x 2 = 18
10 x 9 = 90
9 x 8 = 72
9 x 12 = 108
108 ÷ 9 = 12
18 ÷ 9 = 2
54 ÷ 9 = 6
45 ÷ 9 = 5
81 ÷ 9 = 9
27 ÷ 9 = 3
36 ÷ 9 = 4
72 ÷ 9 = 8
99 ÷ 9 = 11
90 ÷ 9 = 10
63 ÷ 9 = 7

4. 10 for 10
1) a) 25 x 100 =
b) 35.6 x 100 =
2) a) 200 ÷ 100 =
b) 5,000 ÷ 100 =
3) 45.67 + 3.78 =
4) 234 x 6 =
5) What is the value of the underlined digits?
a) 6,187 =
b) 27.82 =
c) 1,568.62 =
6) Round the following to the nearest 10
a) 72 =
b) 287 =
c) 4,712 =

5. ANSWERS
1) a) 25 x 100 = 2,500
b) 35.6 x 100 = 3,560
2) a) 200 ÷ 100 = 2
b) 5000 ÷ 100 = 50
3) 78.71 + 8.23 = 86.94
4) 412 x 6 = 2,472
5) What is the value of the underlined digits?
a) 6187 = 1 hundred or 100
b) 27.82 = 8 tenths or 0.8
c) 1568.62 = 1 thousand or 1,000
6) Round the following to the nearest 10
a) 72 = 70
b) 287 = 290
c) 4,712 = 4,710

6. Coordinates allow us to pinpoint exactly where a point or shape is on
a graph or map.
(the x coordinate)
The first number shows us
how many places to move
across the horizontal axis.
(the y coordinate)
The second number shows us
how many places to move up
the vertical axis.
They are an ‘ordered pair’ of numbers
which means the order in which they are written is important.
Coordinates are written in brackets separated by a
comma, like this (1, 6).

9. Write the co-ordinates of the objects
on the graph

10. ANSWERS
Tree- (1,1)
Football – (2,2)
Hat – (6,1)
Dog- (4,4)
Boot- (1,5)
Teacup- (5,6)

12. Name the coloured shape at
co-ordniates:
• (8,1)
• (10,7)
• (4,5)
• (7,3)
• (1,4)
• (2,7)
• (9,3)
• (6,5)
• (10,1)
• (8,6)

13. ANSWERS
• (8,1) orange square
• (10,7) red triangle
• (4,5) white circle
• (7,3) yellow triangle
• (1,4) green square
• (2,7) orange circle
• (9,3) white triangle
• (6,5) green circle
• (10,1) blue circle
• (8,6) yellow square

14. Extra Challenge!
Which coloured shape’s X (horizontal) co-
ordinate is double it’s Y (vertical) co-ordinate?

15. ANSWER
Orange triangle (10,5)
Why not have a go at drawing your own
co-ordinates treasure map?

16. 05/05/20
WALT: use inverse operations

17. 2 x 3 =
7 x 4 =
5 x 10 =
12 x 2 =
4 x 11 =
5 x 6 =
10 x 4 =
5 x 9 =
4 x 4 =
0 x 2 =
2 x 7 =
2 x 4 =
11 x 5 =
6 x 5 =
4 x 3 =
1 x 5 =
3 x 12 =
9 x 10 =
7 x 2 =
2 x 11 =
0 x 10 =
8 x 5 =
5 x 3 =
10 x 6 =
3 x 10 =
4 x 8 =
2 x 2 =
1 x 4 =
9 x 3 =
5 x 0 =

18. 2 x 3 = 6
7 x 4 = 28
5 x 10 = 50
12 x 2 = 24
4 x 11 = 44
5 x 6 = 30
10 x 4 = 40
5 x 9 = 45
4 x 4 = 16
0 x 2 = 0
2 x 7 = 14
2 x 4 = 8
11 x 5 = 55
6 x 5 = 30
4 x 3 = 12
1 x 5 = 5
3 x 12 = 36
9 x 10 = 90
7 x 2 = 14
2 x 11 = 22
0 x 10 = 0
8 x 5 = 40
5 x 3 = 15
10 x 6 = 60
3 x 10 = 30
4 x 8 = 32
2 x 2 = 4
1 x 4 = 4
9 x 3 = 27
5 x 0 = 0

19. 1) a) 456 x 10 =
b) 3.8 x 10 =
2) a) 450 ÷ 10 =
b) 5 ÷ 10 =
3) Look at this
number: 5,674.32
Which digit is in the
a) Thousands =
b) Hundredths =
4) 4,501 – 2,789 =
5) 873 x 7 =
10 for 10
6) Round these to the nearest 100
a) 287 =
b) 750 =
c) 2395 =
7) Round these to the nearest
whole number
a) 1.4 = b) 3.8 = c) 15.5 =
8) What time is it
a) 20 minutes later than 9:30am?
b) 30 minutes before 2:35pm?
c) 25 minutes after 4:30pm?

20. 1) a) 456 x 10 = 4,560
b) 3.8 x 10 = 38
2) a) 450 ÷ 10 = 45
b) 5 ÷ 10 = 0.5
3) Look at this number:
5,674.32
Which digit is in the
a) Thousands = 5
b) Hundredths = 2
4) 4501 – 2789 = 1,712
5) 873 x 7 = 6,111
ANSWERS
6) Round these to the nearest 100
a) 287 = 300
b) 750 = 800
c) 2,395 = 2,400
7) Round these to the nearest whole
number
a) 1.4 = 1 b) 3.8 = 4 c) 15.5 = 16
8) What time is it
a) 20 minutes later than 9:30am?
9:50am
b) 30 minutes before 2:35pm?
2:05pm
c) 25 minutes after 4:30pm?
4:55pm

21. Division is the opposite (inverse) of multiplication,
and vice versa.
Therefore, if we know 1 calculation, we actually
know 4!
For example, if we know that 5 x 12 = 60
We also know that 12 x 5 = 60
And that 60 ÷ 5 = 12
And 60 ÷ 12 = 5

22. 5 x 12 = 60 so 12 x 5 = 60 so
60 ÷ 5 = 12 so 60 ÷ 12 = 5
When multiplying, the largest number is (usually)
in the answer space and the other two number can
change spaces.
When dividing, the largest number (usually) comes
first and the other two numbers can change
spaces.
Using inverse operations in this way, you will be
able to come up with 4 calculations- 2
multiplication and 2 division.

23. If you know that 7 x 8 = 56…
…then you also know that:
__ x __ = ____ (the largest number is the answer when multiplying)
And
____ ÷ __ = __ (the largest number comes first when dividing)
And
____ ÷ __ = __

24. Use inverse operations to find three
more calculations for the ones below
• If 4 x 8 = 32, then ? And ? And ?
• If 11 x 6 = 66 , then ? And ? And ?
• If 7 x 3 = 21 , then ? And ? And ?
• If 5 x 10 = 50 , then ? And ? And ?
• If 132 ÷ 11 = 12 , then ? And ? And ?
• If 45 ÷ 5 = 9 , then ? And ? And ?
• If 72 ÷ 9 = 8 , then ? And ? And ?
• If 110 ÷ 11 = 10 , then ? And ? And ?

25. ANSWERS
• If 4 x 8 = 32, then 8 x 4 = 32 And 32 ÷ 4 = 8 And 32 ÷ 8 = 4
• If 11 x 6 = 66 , then 6 x 11 = 66 And 66 ÷ 11 = 6 And 66 ÷ 6 = 11
• If 7 x 3 = 21 , then 3 x 7 = 21 And 21 ÷ 7 = 3 And 21 ÷ 3 = 7
• If 5 x 10 = 50 , then 10 x 5 = 50 And 50 ÷ 10 = 5 And 50 ÷ 5 = 10
• If 132 ÷ 11 = 12 , then 132 ÷ 12 = 11 And 12 x 11 = 132 And 11 x 12 = 132
• If 45 ÷ 5 = 9 , then 45 ÷ 9 = 5 And 5 x 9 = 45 And 9 x 5 = 45
• If 72 ÷ 9 = 8 , then 72 ÷ 8 = 9 And 9 x 8 = 72 And 8 x 9 = 72
• If 110 ÷ 11 = 10 , then 110 ÷ 10 = 11 And 10 x 11 = 110 And 11 x 10 = 110

26. This also works for addition and
subtraction
For example, if we know that 124 + 36 = 160
Then we also know that 36 + 124 = 160
And 160 – 124 = 36
And 160 – 36 = 124
When adding, the largest number is the answer and
when subtracting, the largest number comes first.

27. Extra Challenge!
Come up with some of your own sets of addition
and subtraction calculations.
Remember, you only need to know the answer to
one calculation to know the other three.
To start you off…
If 150 + 34 = 184, then…
You could use a calculator to check your answers.

28. 06/05/20
WALT: use bus stop division

29. 10 for 10
1) 8,965 – 3,364 =
2) 543 + 212 + 420 =
3) 80, 77, 74, 71, _?_
4) 6,000 + 2 + five hundreds + eighty =
5) How many minutes are there in quarter of an hour?
6) Write three odd numbers which can be added
together to make 19
7) A ladder is 5….. mm cm m km tall
8) Half of 52 =
9) How many wheels do eight cars have?
10)If you have £1 and spend 36p, how much do you have
left?

30. 10 for 10
1) 8,965 – 3,364 = 5,601
2) 543 + 212 + 420 = 1,175
3) 80, 77, 74, 71, _68_
4) 6,000 + 2 + five hundreds + eighty = 6,582
5) How many minutes are there in quarter of an hour? 15
minutes
6) Write three different odd numbers which can be added
together to make 19 9 + 7 + 3 or 13 + 1 + 5 or 15 + 3 + 1
7) A ladder is 5….. mm cm m km tall
8) Half of 52 = 26
9) How many wheels do eight cars have? 32
10) If you have £1 and spend 36p, how much do you have left?
64p

31. 6 x 2 =
10 x 5 =
3 x 8 =
0 x 3 =
12 x 10 =
3 x 1 =
2 x 8 =
5 x 11 =
10 x 1 =
7 x 5 =
5 x 4 =
9 x 4 =
10 x 10 =
8 x 10 =
11 x 3 =
3 x 6 =
2 x 0 =
2 x 5 =
8 x 3 =
10 x 9 =
5 x 7 =
10 x 2 =
12 x 5 =
4 x 9 =
10 x 3 =
10 x 7 =
2 x 12 =
0 x 4 =
3 x 11 =
6 x 10 =

32. 6 x 2 = 12
10 x 5 = 50
3 x 8 = 24
0 x 3 = 0
12 x 10 = 120
3 x 1 = 3
2 x 8 = 16
5 x 11 = 55
10 x 1 = 10
7 x 5 = 35
5 x 4 = 20
9 x 4 = 36
10 x 10 = 100
8 x 10 = 80
11 x 3 = 33
3 x 6 = 18
2 x 0 = 0
2 x 5 = 10
8 x 3 = 24
10 x 9 = 90
5 x 7 = 35
10 x 2 = 20
12 x 5 = 60
4 x 9 = 36
10 x 3 = 30
10 x 7 = 70
2 x 12 = 24
0 x 4 = 0
3 x 11 = 33
6 x 10 = 60

33. Starter- sort the factors
Factors of
30
Odd
12 1 4 30 14 10 15 2 5 6

34. Watch this short video to remind you
of how to use the bus stop method for
division
https://www.youtube.com/watch?v=SLze82Zcc4Y
Then have a go yourself using the calculations on
the following slides

35. Mild
78 ÷ 3 =
65 ÷ 5 =
84 ÷ 3 =
72 ÷ 3 =
105 ÷ 5 =
135 ÷ 3 =
Spicy
243 ÷ 3 =
300 ÷ 4 =
260 ÷ 4 =
384 ÷ 3 =
756 ÷ 4 =
579 ÷ 3 =
Hot
940 ÷ 4 =
726 ÷ 6 =
868 ÷ 4 =
936 ÷ 6 =
952 ÷ 4 =
972 ÷ 6 =
Extra Hot
2,289 ÷ 7 =
4,188 ÷ 6 =
3,432 ÷ 8 =
5,769 ÷ 9 =
3,528 ÷ 7 =
7,000 ÷ 8 =

36. ANSWERS
Mild
78 ÷ 3 = 26
65 ÷ 5 = 13
84 ÷ 3 = 28
72 ÷ 3 = 24
105 ÷ 5 = 21
135 ÷ 3 = 45
Spicy
243 ÷ 3 = 81
300 ÷ 4 = 75
260 ÷ 4 = 65
384 ÷ 3 = 128
756 ÷ 4 = 189
579 ÷ 3 = 193
Hot
940 ÷ 4 = 235
726 ÷ 6 = 121
868 ÷ 4 = 217
936 ÷ 6 = 156
952 ÷ 4 = 238
972 ÷ 6 = 162
Extra Hot
2,289 ÷ 7 = 327
4,188 ÷ 6 = 698
3,432 ÷ 8 = 429
5,769 ÷ 9 = 641
3,528 ÷ 7 = 504
7,000 ÷ 8 = 875

37. 07/05/20
WALT: find the area of quadrilaterals

38. 10 for 10
1) Find:
a) ½ of 120 b) ½ of 86 c) ¼ of 20 d) ¾ of 100
2) 246 ÷ 6 =
3) 3/8 + 4/8 – 5/8 =
4) 120 ÷ 10 =
5) 2,780 ÷ 100 =
6) A square has sides of 10cm. What is it’s perimeter?
7) If 1,000g = 1kg, then 13,000g = ?kg

39. 10 for 10- ANSWERS
1) Find:
a) ½ of 120- 60 b) ½ of 86- 43 c) ¼ of 20- 5 d) ¾ of 100- 75
2) 246 ÷ 6 = 41
3) 3/8 + 4/8 – 5/8 = 2/8
4) 120 ÷ 10 = 12
5) 2,780 ÷ 100 = 27.8
6) A square has sides of 10cm. What is it’s perimeter? 40cm
7) If 1,000g = 1kg, then 13,000g = 13kg

40. 6 x 9 =
3 x 4 =
2 x 10 =
9 x 12 =
10 x 5 =
0 x 9 =
1 x 6 =
11 x 4 =
2 x 8 =
5 x 12 =
5 x 2 =
11 x 12 =
4 x 8 =
1 x 12 =
0 x 0 =
11 x 6 =
8 x 1 =
9 x 3 =
9 x 7 =
4 x 0 =
20 ÷ 2 =
45 ÷ 9 =
33 ÷ 11 =
30 ÷ 5 =
70 ÷ 10 =
8 ÷ 4 =
5 ÷ 1 =
42 ÷ 6 =
24 ÷ 3 =
60 ÷ 5 =

41. 6 x 9 = 54
3 x 4 = 12
2 x 10 = 20
9 x 12 = 108
10 x 5 = 50
0 x 9 = 0
1 x 6 = 6
11 x 4 = 44
2 x 8 = 16
5 x 12 = 60
5 x 2 = 10
11 x 12 = 132
4 x 8 = 32
1 x 12 = 12
0 x 0 = 0
11 x 6 = 66
8 x 1 = 8
9 x 3 = 27
9 x 7 = 63
4 x 0 = 0
20 ÷ 2 = 10
45 ÷ 9 = 5
33 ÷ 11 = 3
30 ÷ 5 = 6
70 ÷ 10 = 7
8 ÷ 4 = 2
5 ÷ 1 = 5
42 ÷ 6 = 7
24 ÷ 3 = 8
60 ÷ 5 = 12

42. The area of a shape is a measurement of the inside
of the shape.
Area can be measured using centimetres, metres,
kilometres, miles, etc. depending on the size of the
shape being measured.
However, all measurements of area are squared, so
the answer will be followed by this symbol
For example 36cm (read a 36 centimetres squared)
2

43. Different shapes may share the same area
All of these shapes have an area of 9cm

44. You can find the area of a shape by
counting the number of squares inside it
Find the area of the shapes on the following
slide by counting the squares inside them.
Give all measurements in cm

46. ANSWERS
9cm2 14cm2
18cm
2
13cm2

47. But what if there are no squares to count?
If you have a square or rectangular shape, and
you know the measurement for its width and
length, then you can figure out its area by
multiplying the measurements together.
width x length = area

48. For example
10cm
Area- 10cm x 6cm = 60cm
6cm

49. Find the area of the shapes below by multiplying their
width measurement by their height measurement
A
B
C
D
E

50. ANSWERS
A- 6cm x 3cm = 18cm
B- 6cm x 6cm = 36cm
C- 9cm x 5cm = 45cm
D- 2cm x 8cm = 16cm
E – 7cm x 8cm = 56cm
2
2
2
2
2

51. We can figure out the area of this shape by separating it into two
rectangles.
We need to figure out the measurements for each side of the two
rectangles in order to find out the area of each.
Once we know this, we add the two area measurements together to
find the total area of the shape.

52. 8m + 5m
A
B
Area of shape A =
Area of shape B =
Total area of shape =

53. 8m + 5m
A
B
Area of shape A = 5m x 6m = 30m
Area of shape B = 13m x 3m = 39m
Total area of shape = 30m + 39m = 69m
ANSWERS
2
2
2

54. Extra challenge!
Explain the difference between the perimeter of
a shape and the area of a shape.
How many different shapes can you draw with
an area of 20cm ? (you will need a ruler)
Can you draw a shape which has the same
perimeter as its area?

55. 08/05/20
WALT: practice our maths skills

56. Use
https://mathsframe.co.uk/en/resources/resource/
477/Multiplication-Tables-Check to test your quick
fire times tables knowledge.
Then spend some time practicing using
https://www.topmarks.co.uk/maths-games/
and
https://www.mathshed.com/en-gb (your log in is
the same as for spelling shed. If you have any
problems with this, use the email form on the
website to get in touch with your class teacher).