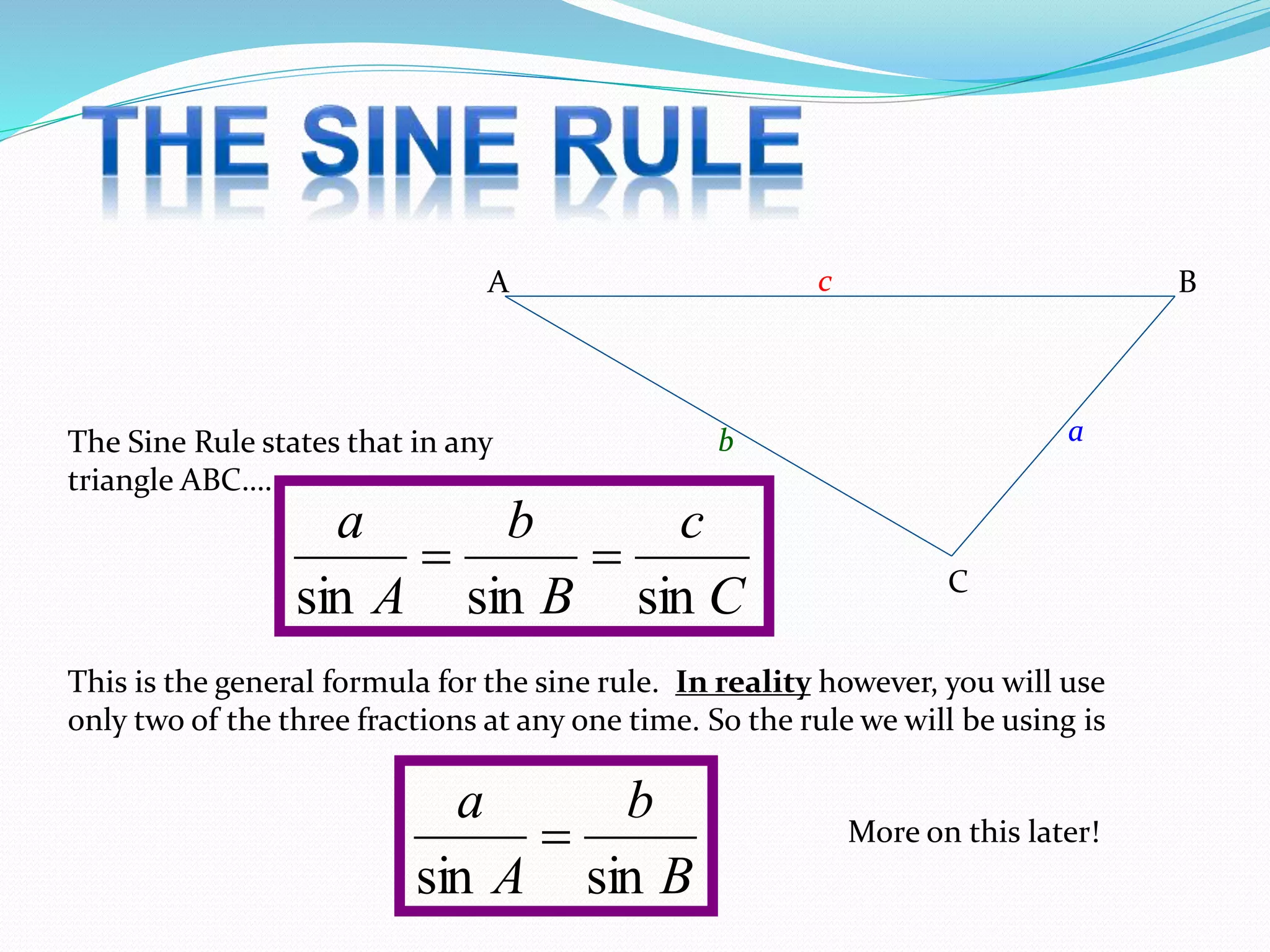
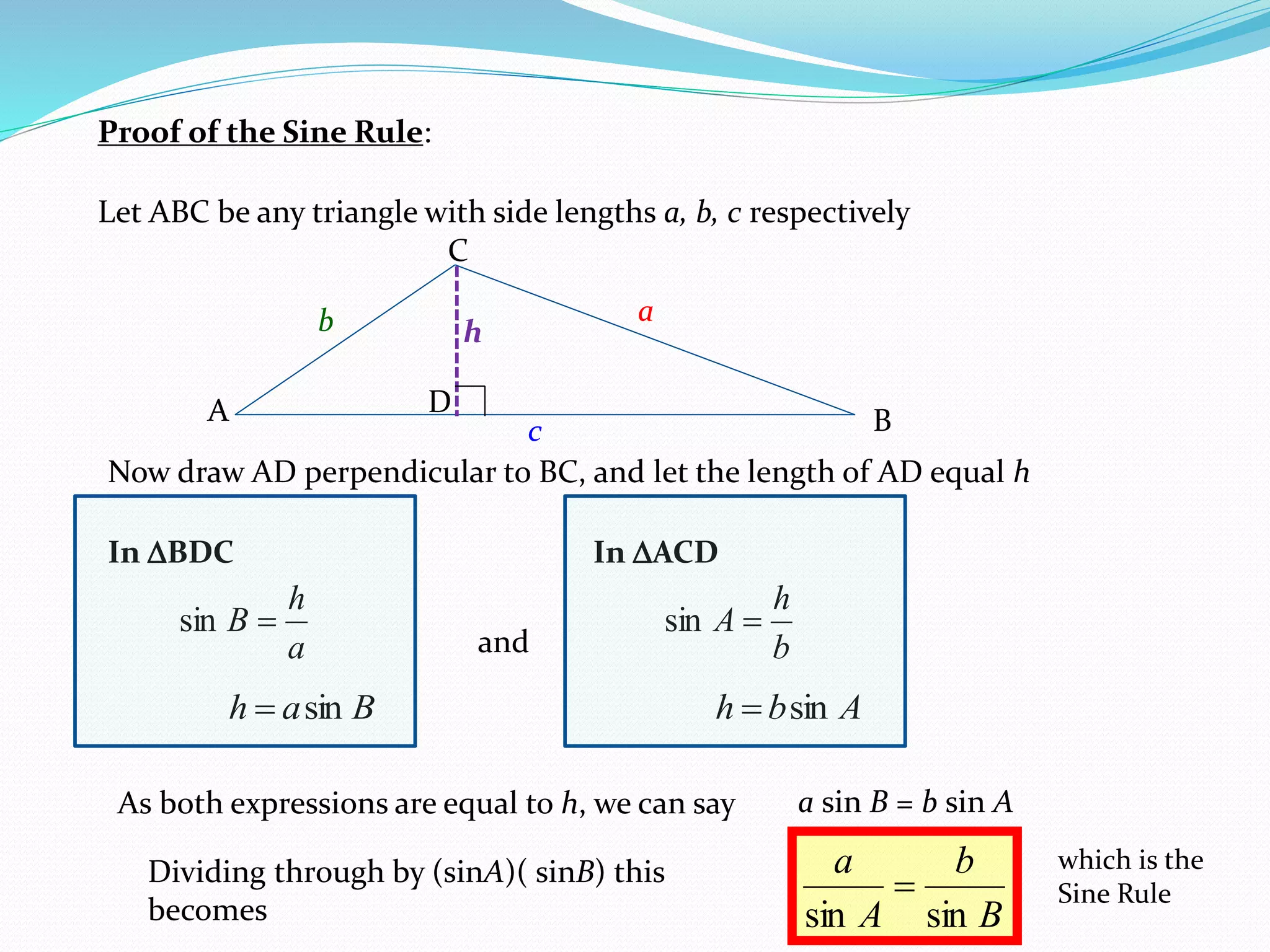
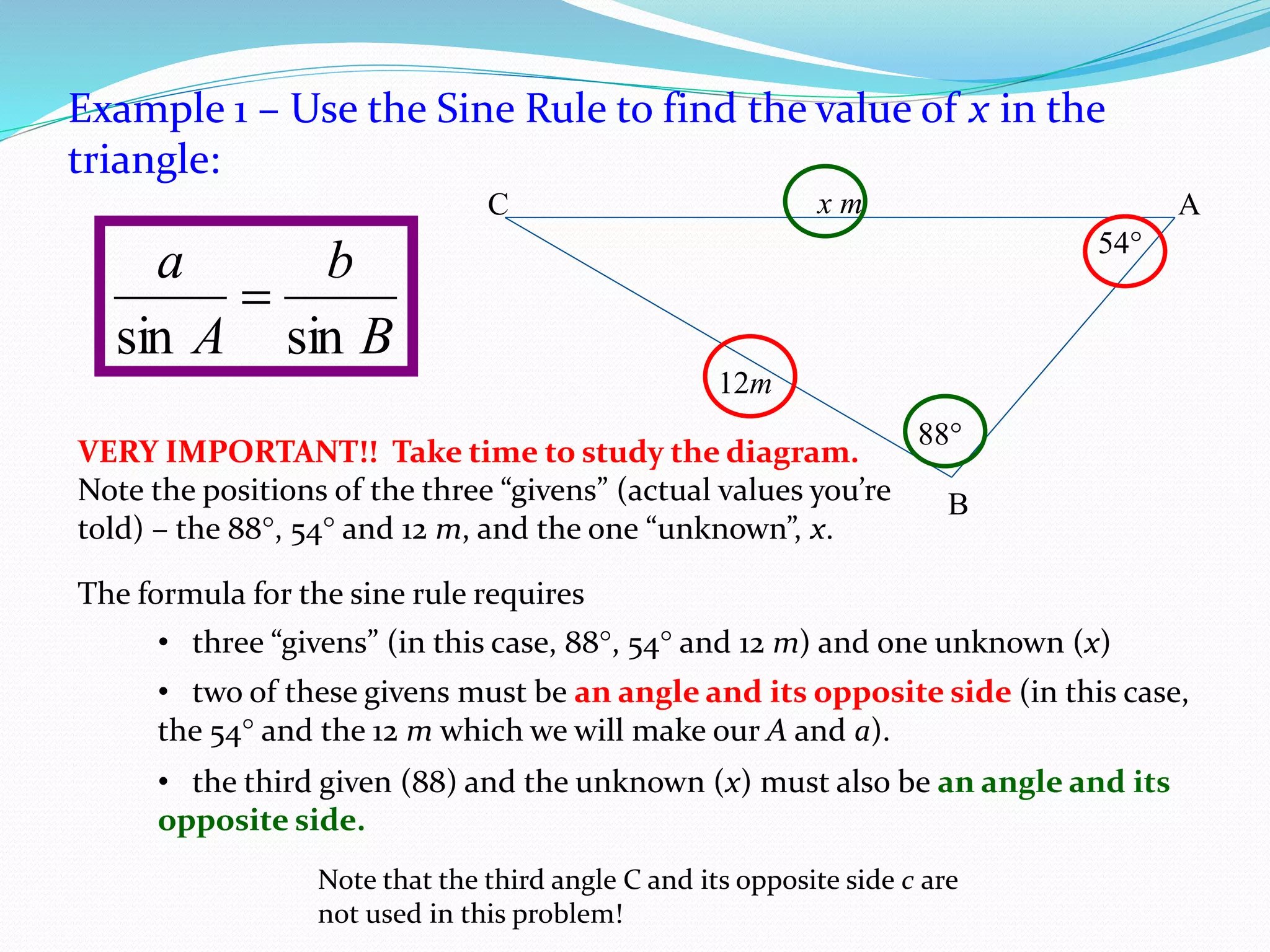
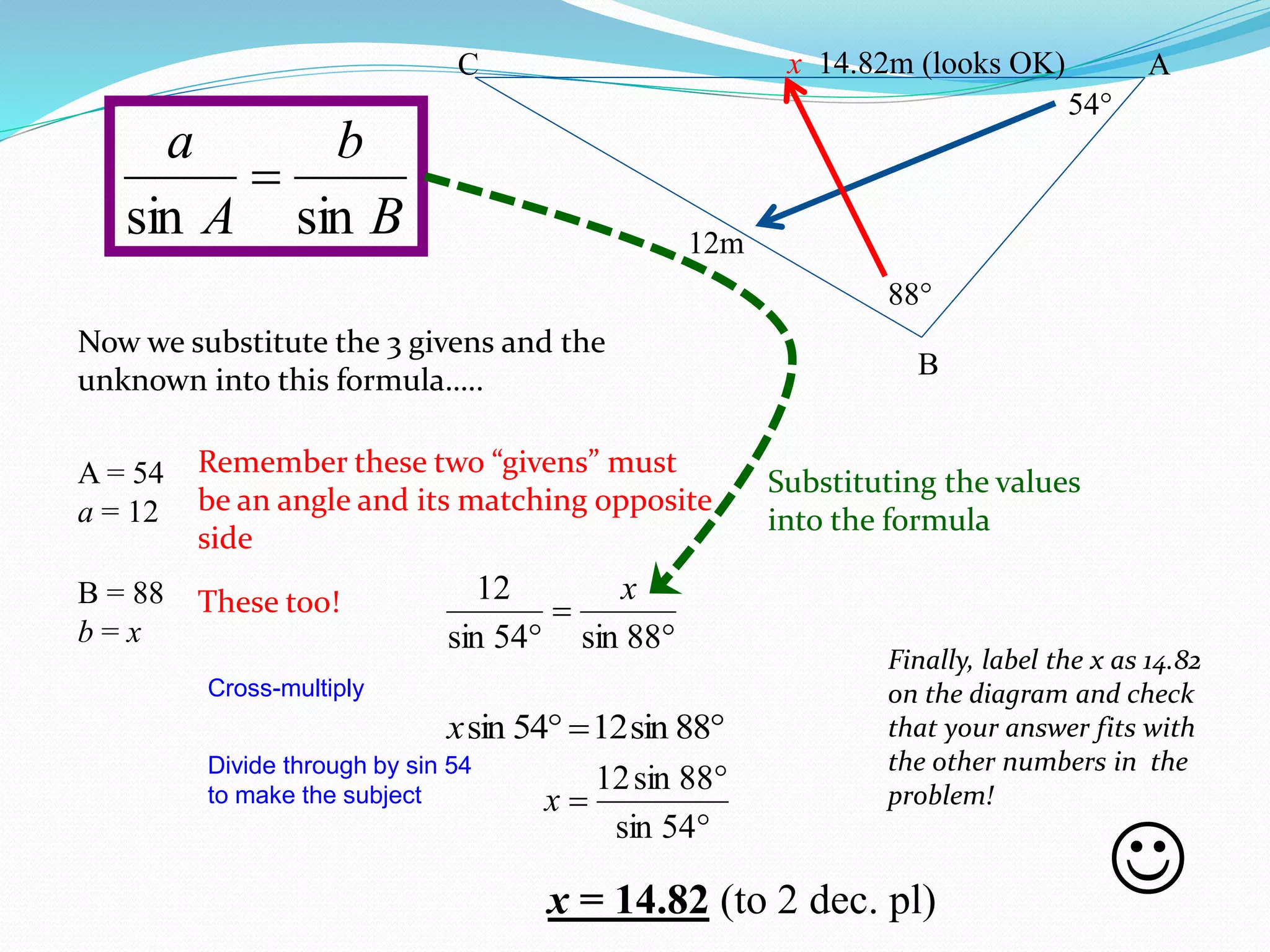
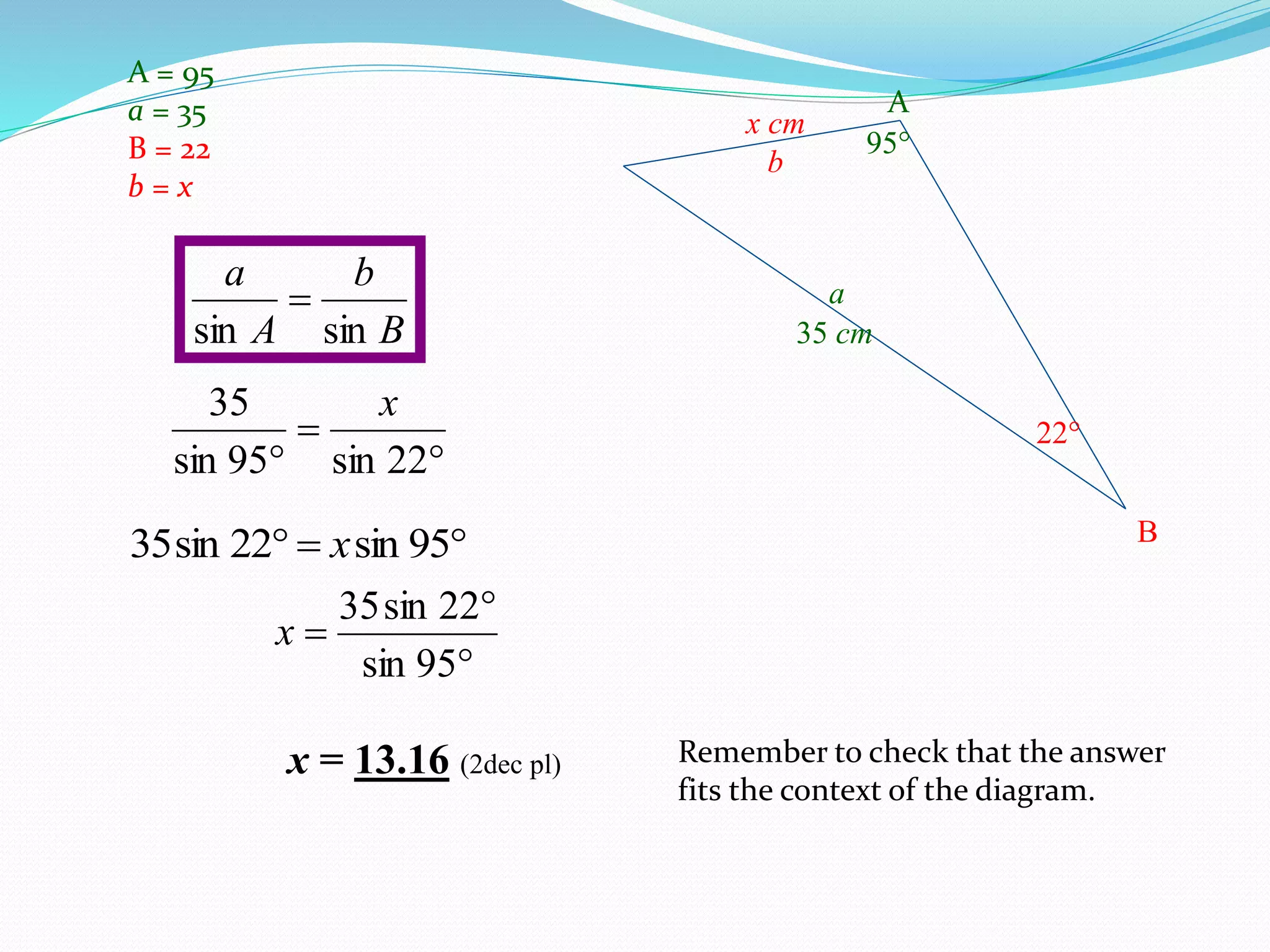
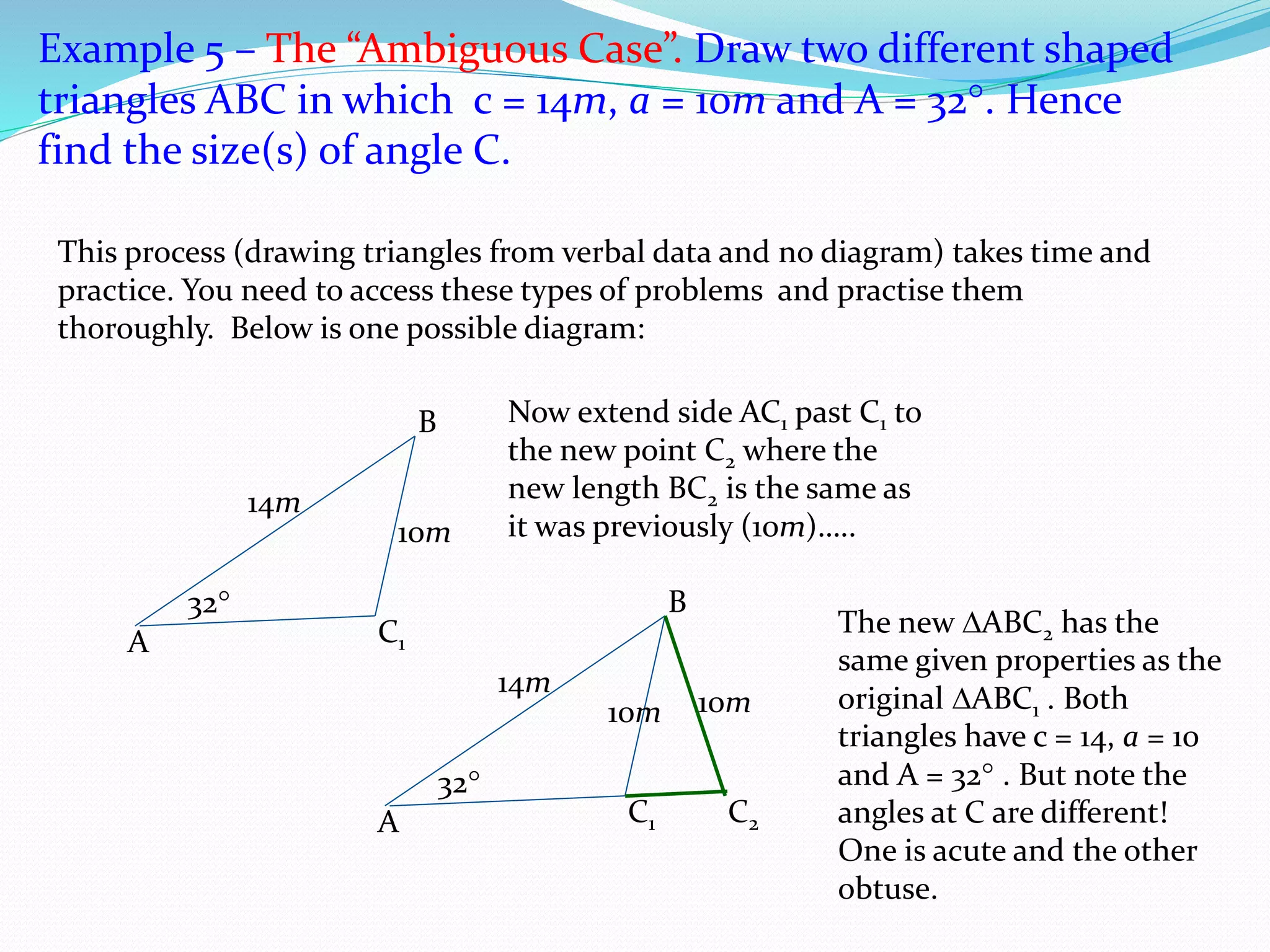
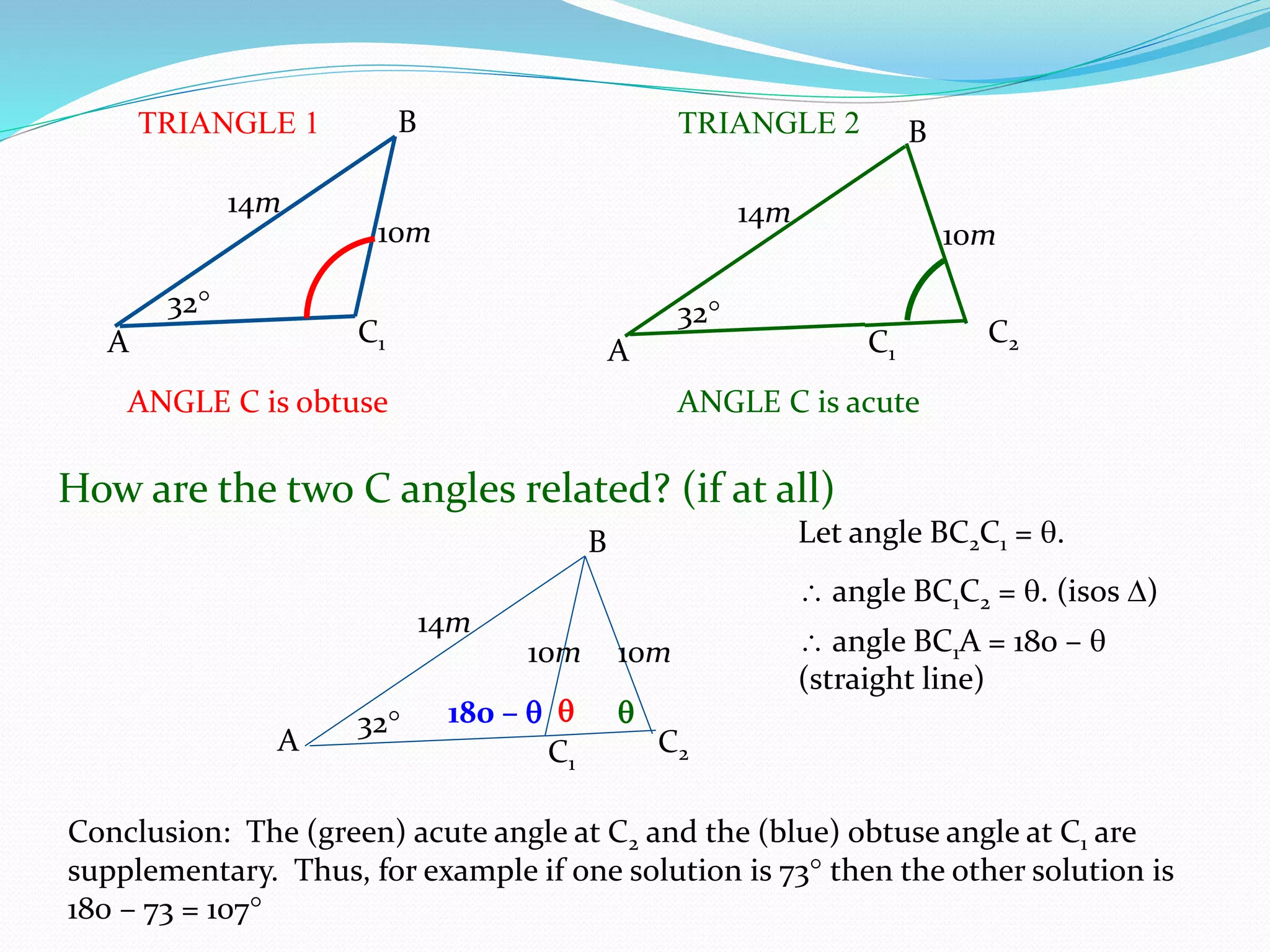
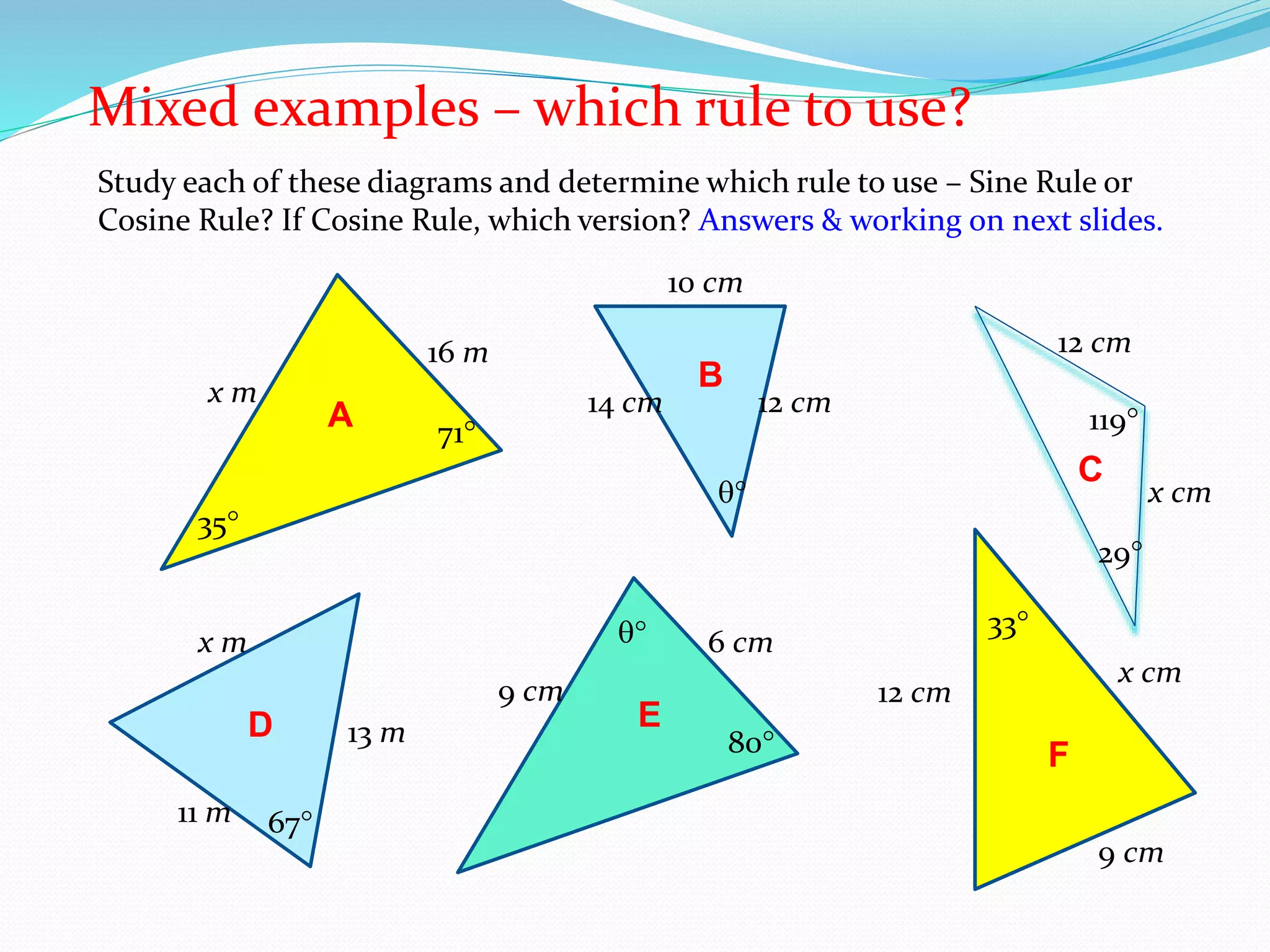
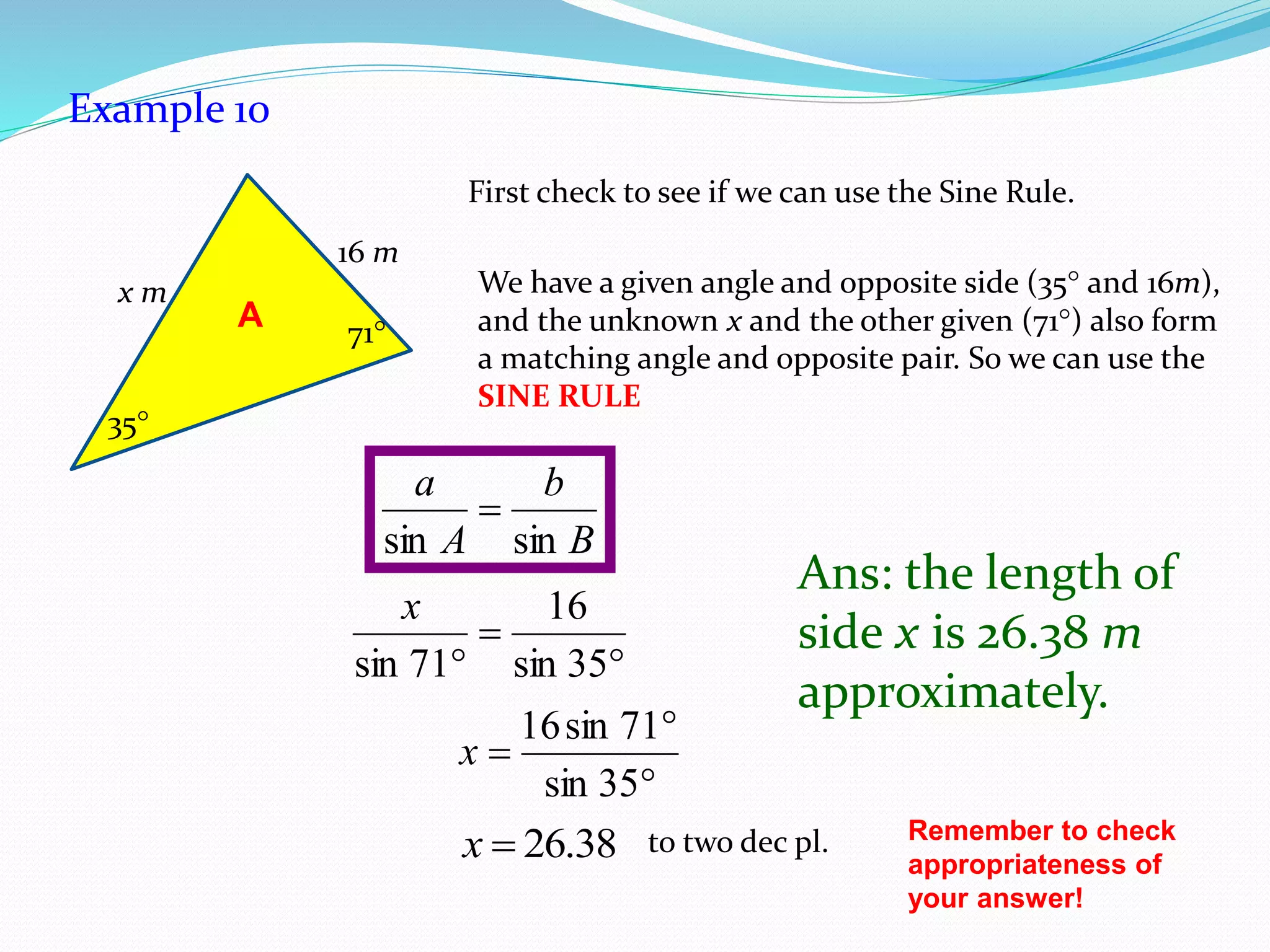
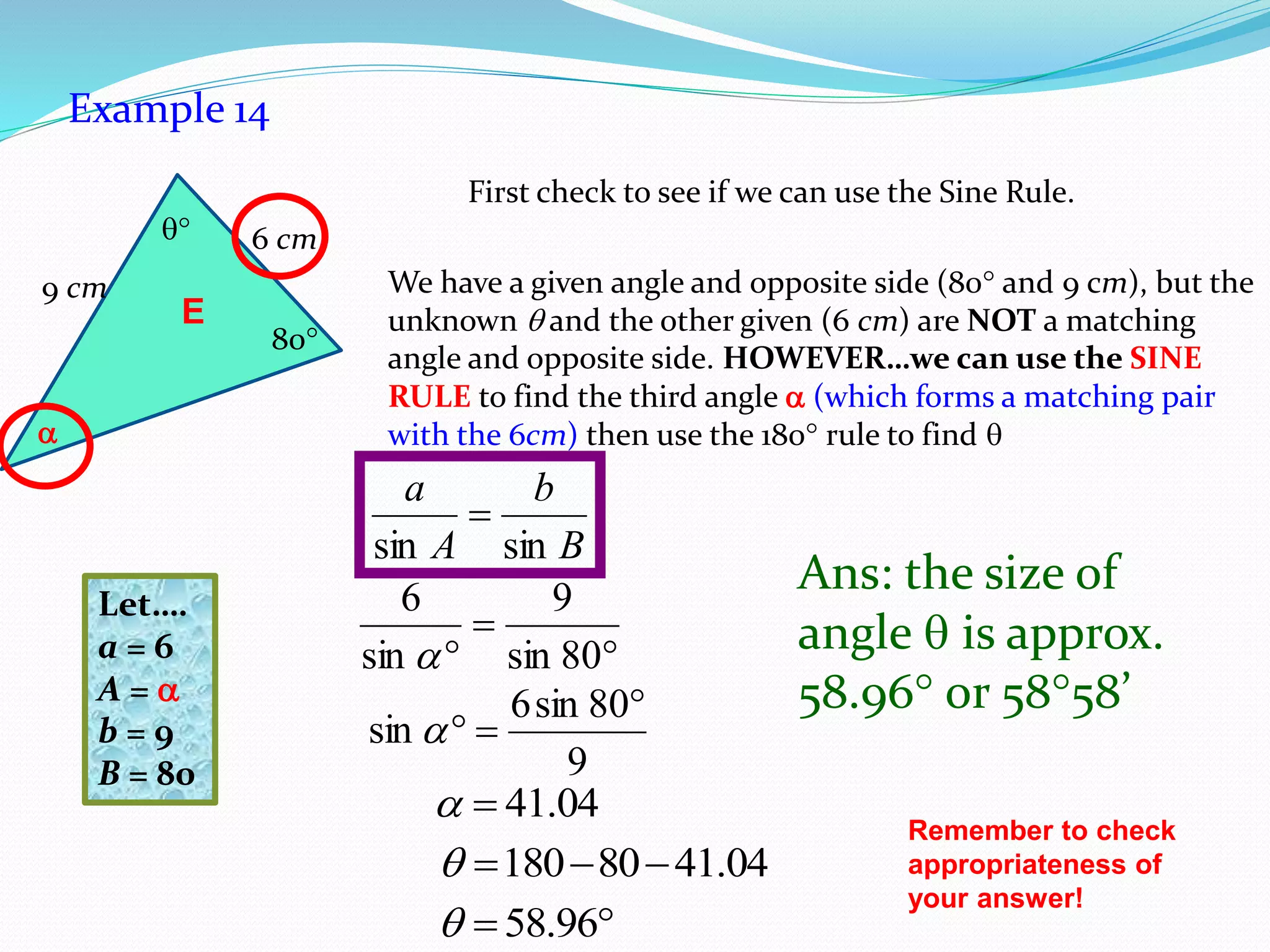
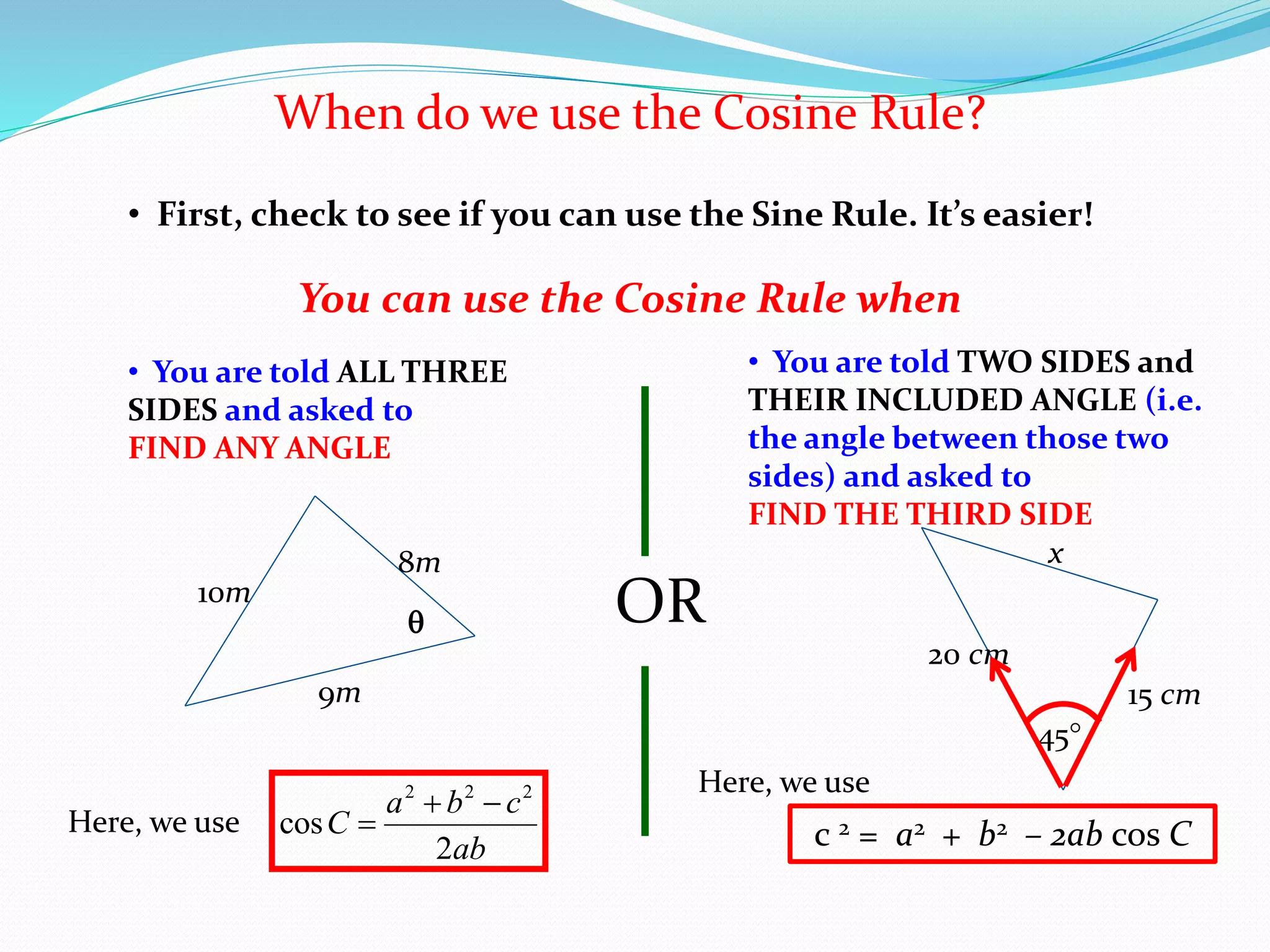
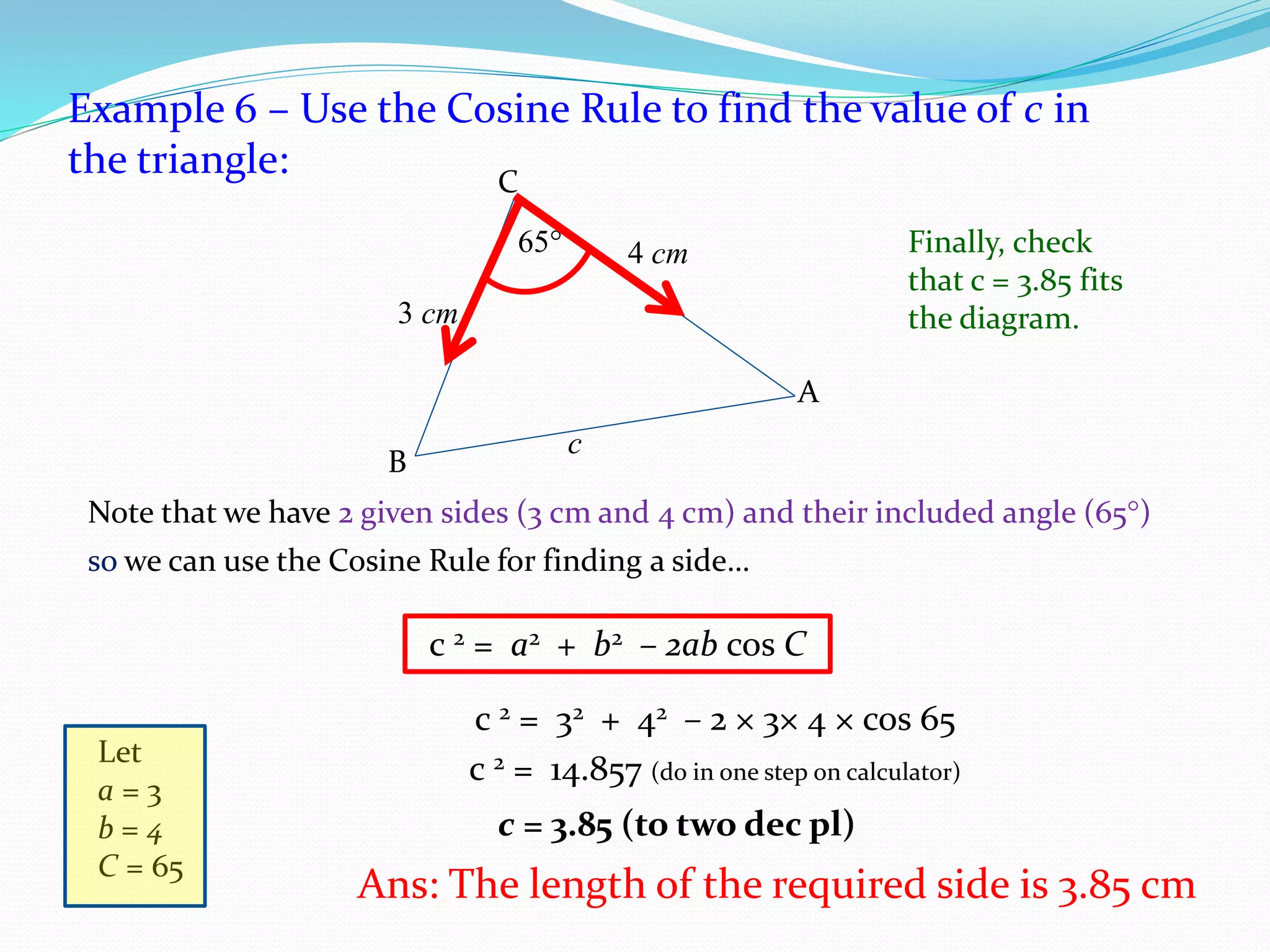
- The Sine Rule and Cosine Rule can be used to find unknown sides and angles in triangles that are not right-angled. - The Sine Rule states that the ratio of the sine of an angle to its opposite side is equal to the ratio of any other angle-side pair. It is generally easier to use than the Cosine Rule. - The Cosine Rule relates all three sides of a triangle to one of its interior angles. It can be used to find a single unknown when three other parts of the triangle are known.

1. Trigonometrical rules for finding sides and angles in
triangles which are not right angled

2. A B
C
First, a word about labelling triangles……
The vertices (corners) of a triangle are usually
labelled using capital letters, for example A, B, C
The sides of the triangle are usually labelled using
lower case letters, in this case, a, b and c, and are
positioned opposite the respective vertices. So
Side a will be opposite vertex A
a
Side b will be opposite vertex B
b
Side c will be opposite vertex C
c
IMPORTANT!!
Note also that side a could also be
called BC as it connects vertex B to
vertex C etc….
(We won’t be using this labelling
system in this unit of work)

3. We will look at the two rules very briefly before starting to use them!

4. A B
C
ab
c
The Sine Rule states that in any
triangle ABC….
C
c
B
b
A
a
sinsinsin

This is the general formula for the sine rule. In reality however, you will use
only two of the three fractions at any one time. So the rule we will be using is
B
b
A
a
sinsin
 More on this later!

5. A B
C
ab
c
The Cosine Rule states that in any
triangle ABC….
Cabbac cos2222

This formula has c2 as the subject, but
the letters can be interchanged, so it
can also be written as
Baccab cos2222

or
Abccba cos2222

Study the patterns and
locations of the letters
in the three formulae
closely. More on the
cosine rule later!

6. The Sine Rule
B
b
A
a
sinsin


7. Proof of the Sine Rule:
Let ABC be any triangle with side lengths a, b, c respectively
C
BA
c
ab
Now draw AD perpendicular to BC, and let the length of AD equal h
h
In BDC
a
h
B sin
Bah sin
In ACD
b
h
A sin
Abh sin
and
As both expressions are equal to h, we can say a sin B = b sin A
Dividing through by (sinA)( sinB) this
becomes B
b
A
a
sinsin

which is the
Sine Rule
D

8. Example 1 – Use the Sine Rule to find the value of x in the
triangle:
C A
B
88
12m
x m
54
VERY IMPORTANT!! Take time to study the diagram.
Note the positions of the three “givens” (actual values you’re
told) – the 88, 54 and 12 m, and the one “unknown”, x.
The formula for the sine rule requires
• three “givens” (in this case, 88, 54 and 12 m) and one unknown (x)
Note that the third angle C and its opposite side c are
not used in this problem!
• two of these givens must be an angle and its opposite side (in this case,
the 54 and the 12 m which we will make our A and a).
• the third given (88) and the unknown (x) must also be an angle and its
opposite side.
B
b
A
a
sinsin


9. C A
B
88
12m
x
54
B
b
A
a
sinsin

Now we substitute the 3 givens and the
unknown into this formula…..
A = 54
a = 12
Remember these two “givens” must
be an angle and its matching opposite
side
B = 88
b = x 

 88sin54sin
12 x
Cross-multiply
 88sin1254sinx
Divide through by sin 54
to make the subject



54sin
88sin12
x
x = 14.82 (to 2 dec. pl)
Substituting the values
into the formula
Finally, label the x as 14.82
on the diagram and check
that your answer fits with
the other numbers in the
problem!
14.82m (looks OK)
These too!


10. Example 2 – Use the Sine Rule to find the value of x in the
triangle:
95
35cm
x cm
22
Here, no vertices are labelled so we
will have to create our own. But
first…
Step 1, check that there are 4 “labels” – i.e. 3
givens and 1 unknown. There are a 95, 22,
35 cm and x cm so this fits our requirements.
Step 2, check that 2 of the 3 givens are a matching angle and
opposite side. 95 and 35 cm fit this. Also check that the remaining
given and the unknown form another matching angle and opposite
side (22 and x cm). They do! All our requirements are in place so we
can now use the Sine Rule!
Step 3, Allocate letters A, a, B, b (or any
other letters of your choice) to matching
pairs.
A = 95
a = 35
B = 22
b = x

11. A = 95
a = 35
B = 22
b = x
B
b
A
a
sinsin



 22sin95sin
35 x
 95sin22sin35 x



95sin
22sin35
x
x = 13.16 (2dec pl) Remember to check that the answer
fits the context of the diagram.
95
35 cm
x cm
22
A
a
B
b

12. Example 3 – Use the Sine Rule to find the value of  in the
triangle:
62

4.7m
5.1m
A quick check indicates everything is in place to use the Sine Rule….
• 3 givens and one unknown
• One pair of givens (5.1 and 62) form a matching angle and opposite side; and
• The other pair (4.7 and ) form the second matching angle and opposite side.
Note the third side and angle are unmarked – we don’t use these.

13. 62

4.7m
5.1m

 62sin
1.5
sin
7.4

B
b
A
a
sinsin

sin1.562sin7.4 
1.5
62sin7.4
sin


8137.0sin 
 8137.0sin 1

'2854459.54  or Remember to check that the answer
fits the context of the diagram.

14. Example 4 – Use the Sine Rule to find the value of x in the
triangle:
68
33
x m
35.7m
Looking at the diagram, it seems we have a
problem! 
Although the 68 and 35.7 form a matching angle
and opposite side, the 33 and x do not.
But…remembering the angle sum of a triangle is 180,
we can work out the 3rd angle to be 180 – 33 – 68 = 79.
So now we use the 79 as the matching angle for the x and
proceed as usual, ignoring the 33 which plays no further part.


 68sin
7.35
79sin
x
79



68sin
79sin7.35
x
x = 37.80 (2 dec pl)

15. Example 5 – The “Ambiguous Case”. Draw two different shaped
triangles ABC in which c = 14m, a = 10m and A = 32. Hence
find the size(s) of angle C.
A
B
14m
32
C1
10m
This process (drawing triangles from verbal data and no diagram) takes time and
practice. You need to access these types of problems and practise them
thoroughly. Below is one possible diagram:
Now extend side AC1 past C1 to
the new point C2 where the
new length BC2 is the same as
it was previously (10m)…..
A
B
14m
32
C1
10m
C2
10m
The new ABC2 has the
same given properties as the
original ABC1 . Both
triangles have c = 14, a = 10
and A = 32 . But note the
angles at C are different!
One is acute and the other
obtuse.

16. A
B
14m
32
C1
10m
ANGLE C is obtuse
B
14m
32
C1
C2
10m
A
TRIANGLE 1 TRIANGLE 2
ANGLE C is acute
How are the two C angles related? (if at all)
A
B
14m
32
C1
10m
C2
10m
Let angle BC2C1 = .

 angle BC1C2 = . (isos )

 angle BC1A = 180 – 
(straight line)
180 – 
Conclusion: The (green) acute angle at C2 and the (blue) obtuse angle at C1 are
supplementary. Thus, for example if one solution is 73 then the other solution is
180 – 73 = 107

17. Back to the question!
Draw the triangle with the acute, rather than the obtuse, angle
at C.
Applying the Sine Rule,


 sin
14
32sin
10
B
14m
32
C2
10m
A

10
32sin14
sin 
 9.47
One solution (the acute angle which is
the only one given by the calculator) is
therefore 47.9 and the second solution
(the obtuse angle) is 180 – 47.9 = 132.1
Ans:  = 47.9 or 132.1

18. • The Sine Rule can be used to find unknown sides or angles in triangles.
• The Sine Rule formula is C
c
B
b
A
a
sinsinsin

• To use the Sine Rule, you must have
 A matching angle and opposite side pair (two givens)
 A third given and an unknown, which also make an angle
and opposite side pair
• When confronted with a problem where you have to decide whether to use
the Sine Rule or the Cosine Rule, always try for the Sine Rule first, as it is easier.
We will have this discussion later!
• When asked to find the size of an ANGLE, first check whether the problem
could involve the ambiguous case (see Example 5). In that case, the two
answers are supplementary – i.e. add to 180
• In every triangle, the largest side is always opposite the largest angle. The
side lengths are in the ratio of the sines of their opposite angles.

19. In every triangle,
 The largest side is always opposite the largest angle.
 The middle sized side is always opposite the middle sized angle, and
 The smallest side is always opposite the smallest angle
• The ratio of any two side lengths is always equal to the ratio of the sines of their
respective opposite angles.
a
b c
C B
A
..
sin
sin
sin
sin
..
etc
A
C
a
c
B
A
b
a
ei


These are just re-shaped versions of
the original sine rule formulae.

20. The Cosine Rule
There are two variations of this….
To find a side use
c2 = a2 + b2 – 2ab cos C
To find an angle use
ab
cba
C
2
cos
222


These formulae are just rearrangements of each
other. Verify this as an exercise.

21. Proof of the Cosine Rule:
Let ABC be any triangle with side lengths a, b, c respectively
A
BC
a
cb
Now draw AD perpendicular to BC, and let the length of AD equal h
h
In ACD
b
x
C cos
In ABD
Pythagoras gives
222
)( xahc 
D
Let the length CD = x, and so length BD will be a – x.
x a – x
Cbx cos (1)
2222
2 xaxahc 
(2)
In ACD
Pythagoras gives
222
xhb 
222
xbh  (3)
2222
2 xaxach 
The formulae (2) and (3) are both for h2 so we make them equal to each other.
NOTE!! The expansion
(a – x)2 = a2 – 2ax + x2

22. 22222
2 xbxaxac 
Now cancel the x2 on each side and make c 2
the subject…
axbac 2222

From the first box on the previous slide, taking result (1)
x = b cos C
(4)
and substituting this into (4), we get
Cabbac cos2222

which is a version of the Cosine Rule (for finding a side)

23. c 2 = a2 + b2 – 2ab cos C
(1) Note the positions of the letters. If the 2ab cos C were missing, this would just
be Pythagoras’Theorem, c 2 = a2 + b2 . If the triangle were right angled, then C
would be 90 and as cos 90 = 0, it becomes Pythagoras’ Theorem!
(2) When c2 is the subject, the only angle in the formula is C (the angle opposite
to side c). Note A and B are absent from the formula.
(3) The above formula is to find a side length. The letters can be swapped
around and the same formula can be written
b 2 = a2 + c2 – 2ac cos B
a 2 = b2 + c2 – 2bc cos A
c 2 = a2 + b2 – 2ab cos C
Here are the three
variations of the
formula shown
together. Study
them closely and
note the patterns!

24. c 2 = a2 + b2 – 2ab cos C
(4) This formula can be rearranged to make cos C the subject, i.e.
ab
cba
C
2
cos
222


This is the version of the
Cosine Rule to use when
FINDING AN ANGLE.
(5) Again, the letters can be swapped around and the same formula can be written
bc
acb
A
2
cos
222


ac
bca
B
2
cos
222


ab
cba
C
2
cos
222



25. When do we use the Cosine Rule?
• First, check to see if you can use the Sine Rule. It’s easier!
• You are told ALL THREE
SIDES and asked to
FIND ANY ANGLE
You can use the Cosine Rule when
OR
8m
9m
10m

• You are told TWO SIDES and
THEIR INCLUDED ANGLE (i.e.
the angle between those two
sides) and asked to
FIND THE THIRD SIDE
20 cm
45
15 cm
x
Here, we use
ab
cba
C
2
cos
222


Here, we use
c 2 = a2 + b2 – 2ab cos C

26. Example 6 – Use the Cosine Rule to find the value of c in
the triangle:
Note that we have 2 given sides (3 cm and 4 cm) and their included angle (65)
65 4 cm
c
C
3 cm
A
B
c 2 = a2 + b2 – 2ab cos C
Let
a = 3
b = 4
C = 65
c 2 = 32 + 42 – 2 × 3× 4 × cos 65
c 2 = 14.857 (do in one step on calculator)
c = 3.85 (to two dec pl)
Ans: The length of the required side is 3.85 cm
Finally, check
that c = 3.85 fits
the diagram.
so we can use the Cosine Rule for finding a side…

27. Example 7 – Use the Cosine Rule to find the size of C in the
triangle:
Note that we have 3 given sides and are asked to find angle at C (opposite 7.5)
7.5 m
8 m
?
B
9 m
C
A
Let
a = 8
b = 9
c = 7,5
Ans: Angle C is equal to 51.95 (to 2 dec pl)
or 5157’ (to nearest minute)
Finally, check
that C = 51.95 fits
the diagram.
so we can use the Cosine Rule for finding an angle…
ab
cba
C
2
cos
222


Caution! Here we MUST make c =
7.5 as it is the side opposite the
angle we’re finding, i.e. C, whereas a
and b are interchangeable.
 
 982
5.798
cos
222


C
= 0.6163
NOTE !! Bracket
numerator and
denominator
when entering
into calculator.
)6163.0(cos 1
C
95.51C

28. Example 8 – Use the Cosine Rule to find the value of x in
the triangle:
Note that we have 2 given sides (10 m and 11 cm) and their included angle (100)
11 m
x
10 m
c 2 = a2 + b2 – 2ab cos CLet
a = 10
b = 11
c = x
C = 100
x 2 = 102 + 112 – 2 × 10 × 11 × cos 100
x 2 = 259.2 (do in one step on calculator)
x = 16.10 (to two dec pl)
Ans: The length of the required side is 16.10 m
Finally, check
that x = 16.10 fits
the diagram. x is
the longest side
so this would
seem reasonable.
so we use the Cosine Rule for finding a side…

29. Example 9 – Use the Cosine Rule to find the value of  in
the triangle:

29 mm
21 mm
40 mm
Note that we have 3 given sides and are asked to find angle opposite to 40 mm
so we use the Cosine Rule for finding an angle…
ab
cba
C
2
cos
222


Let
a = 21
b = 29
c = 40
C = 
 
 29212
402921
cos
222



2611.0
)2611.0(cos 1
 

= 105.13
Ans:  is approx. equal to
105.13 (to 2 dec pl) or
1058’ (to nearest min)
remember the brackets
Note the negative cos. This means our angle is obtuse!
ALL OBTUSE ANGLES HAVE A NEGATIVE COSINE!
Finally, check that  = 105 fits the diagram. 
LOOKS obtuse so this would seem
reasonable. Beware – you can’t always
presume the drawings are to scale, so be
careful when judging the appropriateness of
your answers (in all problems)

30. • The Cosine Rule can be used to find unknown sides or angles in triangles.
• There are two versions of the Cosine Rule formula and three variations within
each of these, depending on what is required as the subject
ab
cba
C
2
cos
222

c 2 = a2 + b2 – 2ab cos C
To find a SIDE To find an ANGLE
a 2 = b2 + c2 – 2bc cos A
b2 = a2 + c2 – 2ac cos B
bc
acb
A
2
cos
222


ac
bca
B
2
cos
222


Make sure you familiarise yourself with how the PATTERNS in these
configurations work. Also remember each formula on the left is just a
rearrangement of its corresponding formula on the right.

31. • To use the Cosine Rule to find an angle you must be given all three sides
• When deciding whether to use the Sine Rule or the Cosine Rule, always try
the Sine Rule first, as it is easier (only one formula to deal with).
• To use the Cosine Rule to find a side you must be given the other two sides
and their included angle.
• When dealing with angles in the range 90 <  < 180, i.e. OBTUSE
ANGLES, remember that their cosines are negative. This does not apply to
their sines – they are still positive.

32. Mixed examples – which rule to use?
Study each of these diagrams and determine which rule to use – Sine Rule or
Cosine Rule? If Cosine Rule, which version? Answers & working on next slides.
A
35
71
x m
16 m
E

80
9 cm
6 cm
C
29
119
x cm
12 cm
B

14 cm
10 cm
12 cm
D
67
x m
11 m
13 m
F
33
9 cm
x cm
12 cm

33. A
35
71
x m
16 m
Example 10
First check to see if we can use the Sine Rule.
We have a given angle and opposite side (35 and 16m),
and the unknown x and the other given (71) also form
a matching angle and opposite pair. So we can use the
SINE RULE
B
b
A
a
sinsin



 35sin
16
71sin
x



35sin
71sin16
x
38.26x to two dec pl.
Ans: the length of
side x is 26.38 m
approximately.
Remember to check
appropriateness of
your answer!

34. Example 11
First check to see if we can use the Sine Rule.
We are not given any angle so we can’t use the Sine Rule
so we have to use the COSINE RULE – the angle
version
Ans: the size of
angle  is 44.42 or
4425’ approx.
Remember to check
appropriateness of
your answer!
B

14 cm
10 cm
12 cm
ab
cba
C
2
cos
222


Let….
C = 
c = 10
a = 12
b = 14
 
 14122
101412
cos
222



7143.0cos 
7143.0cos 1

42.44

35. Example 12
First check to see if we can use the Sine Rule.
We have a given angle and opposite side (29 and 12cm),
but the unknown x and the other given (119) are NOT a
matching angle and opposite pair. BUT…the third angle is
180 – 119 – 29 = 32 so we can use the SINE RULE
B
b
A
a
sinsin




29sin
32sin12
x
12.13x to two dec pl.
Ans: the length of
side x is 13.12 cm
approximately.
Remember to check
appropriateness of
your answer!
C
29
119
x cm
12 cm
32


 29sin
12
32sin
xLet….
a = x
A = 32
b = 12
B = 29

36. Example 13
First check to see if we can use the Sine Rule.
We are not given any angle and matching opposite side
so we can’t use the Sine Rule, so we have to use the
COSINE RULE – the side version
Ans: the size of side x is
13.35 m (to 2 dec places)
Remember to check
appropriateness of
your answer!
Let….
C = 67
c = x
a = 11
b = 13
D
67
x m
11 m
13 m
c 2 = a2 + b2 – 2ab cos C
x 2 = 112 + 132 – 2 × 11 × 13 × cos 67
x 2 = 178.251
x = 13.35

37. Example 14
First check to see if we can use the Sine Rule.
We have a given angle and opposite side (80 and 9 cm), but the
unknown  and the other given (6 cm) are NOT a matching
angle and opposite side. HOWEVER…we can use the SINE
RULE to find the third angle  (which forms a matching pair
with the 6cm) then use the 180 rule to find 
B
b
A
a
sinsin

Ans: the size of
angle  is approx.
58.96 or 5858’
Remember to check
appropriateness of
your answer!


 80sin
9
sin
6

Let….
a = 6
A = 
b = 9
B = 80
E

80
9 cm
6 cm

9
80sin6
sin


04.41
04.4180180 
 96.58

38. Example 15
F
33
9 cm
x cm
12 cm
First check to see if we can use the Sine Rule.
We have a given angle and opposite side (33 and 9 cm), but the
unknown x and the other given (12 cm) are insufficient data for
Sine Rule. The Cosine Rule won’t work either as the triangle’s
data does not match either of the two configurations for the
Cosine Rule. HOWEVER…if we let  be the angle opposite the
12cm we then have a second matching pair and can begin with
using the SINE RULE to find angle . (This is PART 1)
NOW FOR PART 2 …..Once we know  we can then find the
third angle  (which is opposite to x) and then apply the Sine
Rule a second time to find x.


Part 1 (finding )


 33sin
9
sin
12

9
33sin12
sin


57.46
Finding 
 = 180 – 33 – 46.57
 = 100.43
Part 2 (finding x)


 33sin
9
43.100sin
x
25.16x
Note!! Here the diagram is quite out of
scale. This becomes apparent on checking
the reasonableness of your answer