Embed presentation
Downloaded 285 times









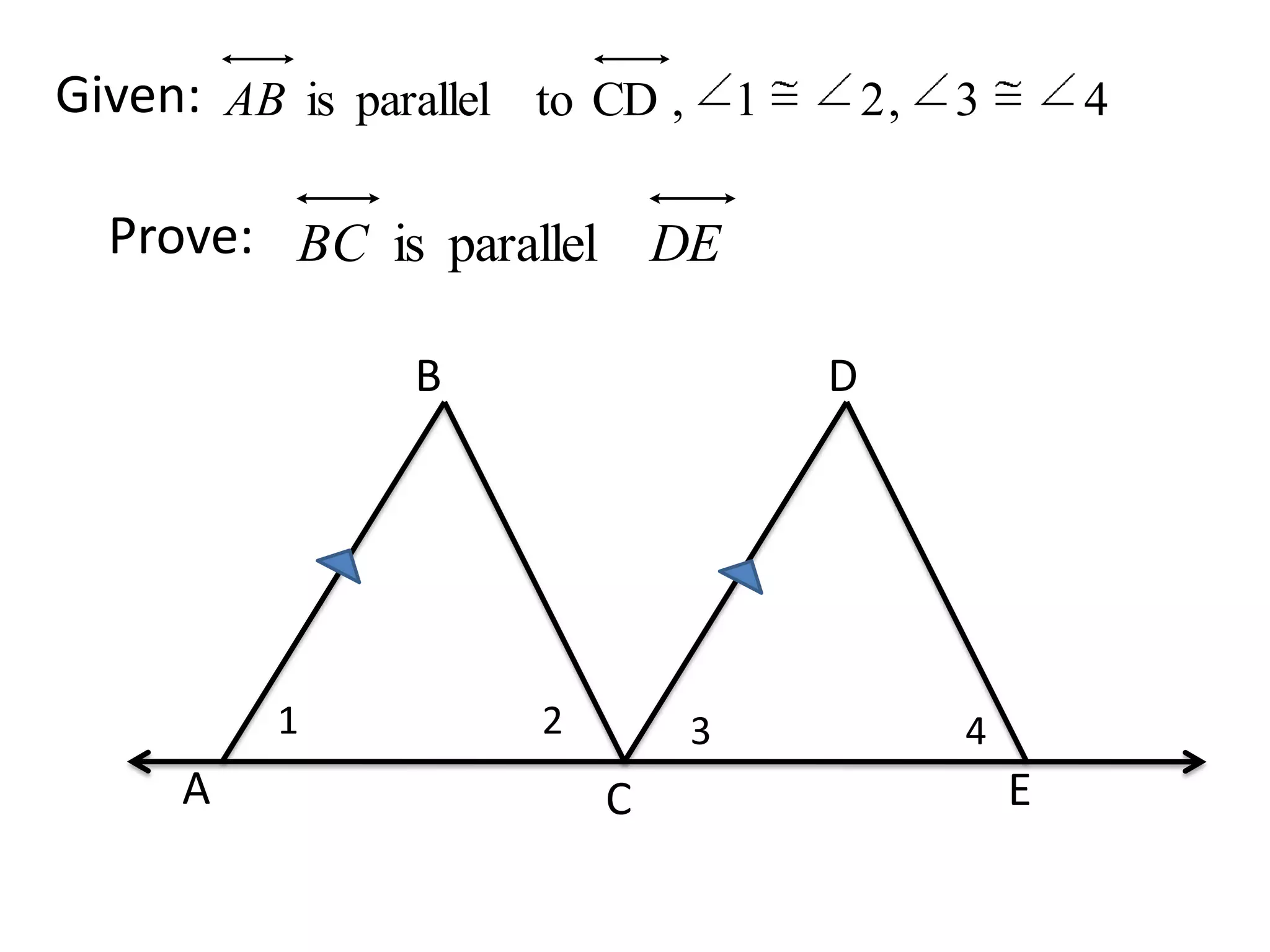



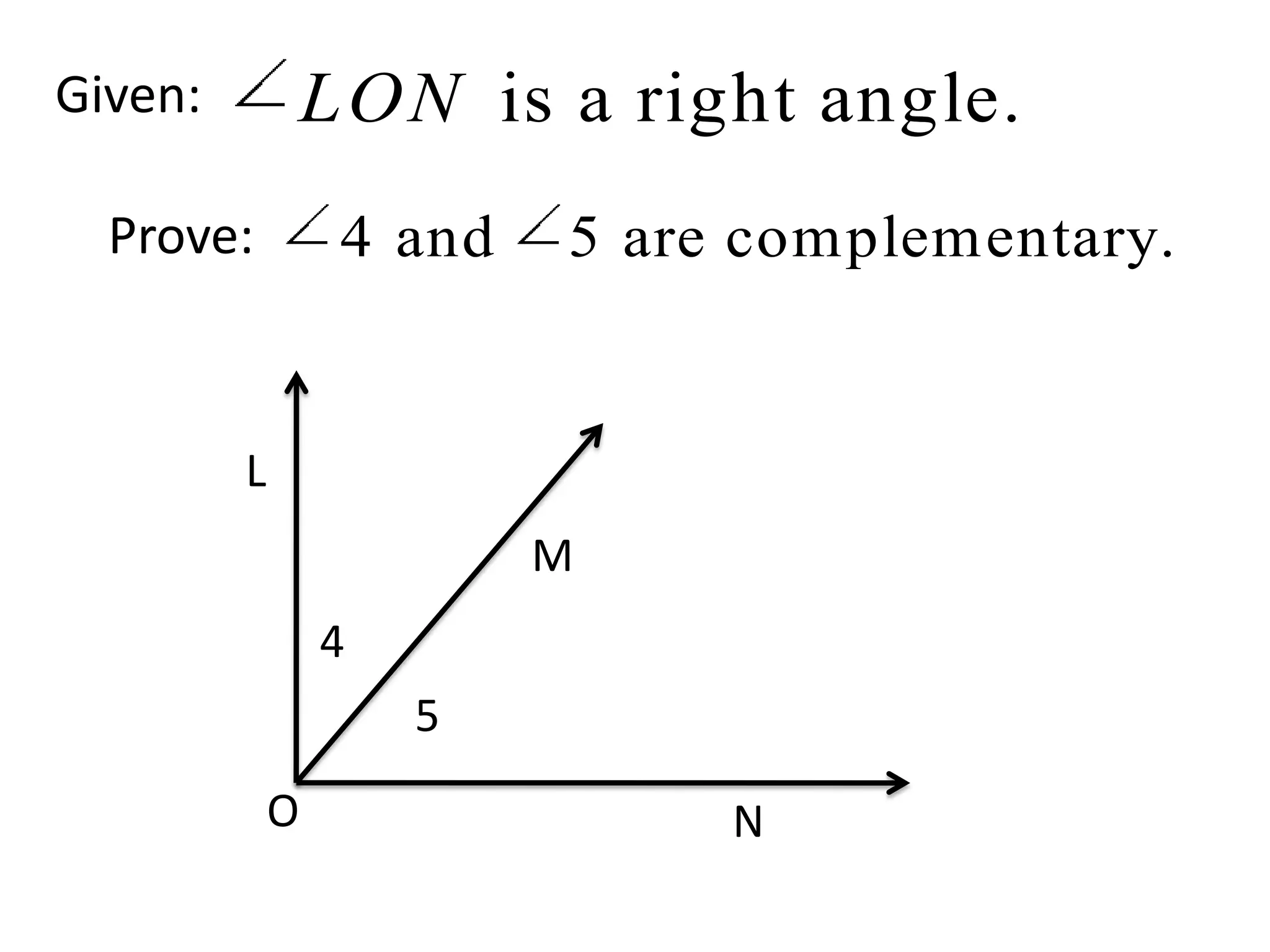



The document outlines geometric proofs, specifically two-column proofs that consist of statements and reasons. It includes examples of proofs involving supplementary angles, congruence, right angles, and various postulates and properties, along with a quiz section. Key components referenced include given information, definitions, postulates, theorems, and properties used in proving geometric statements.




















Introduction to the topic of geometric proofs dated 27 October 2009.
Five key elements: Given, Diagrams, Prove, Statements, Reasons essential for two column proofs.
Identifies reasons for proofs: Given Information, Definitions, Postulates, Properties, Theorems.
Example format of a proof showing 'Given' and 'Prove' sections with statements and reasons listed.
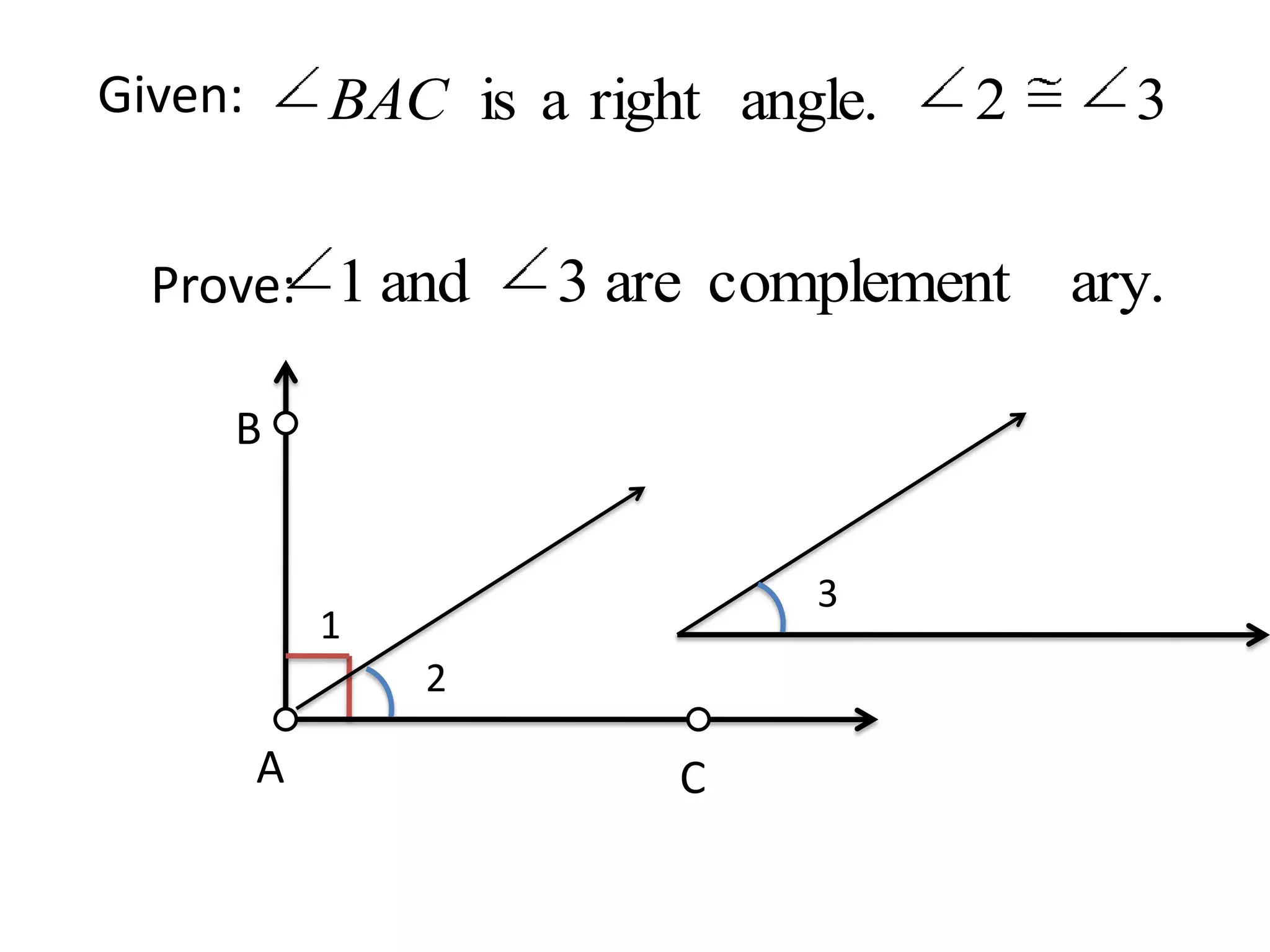
Visual representation of a geometric proof problem with points A, B, and C.
Further examples showing statements and corresponding reasons utilized in geometric proofs.
A specific geometric proof challenge involving measures and angles.
Engaging quiz questions addressing fundamental concepts of geometric proofs and characteristics.
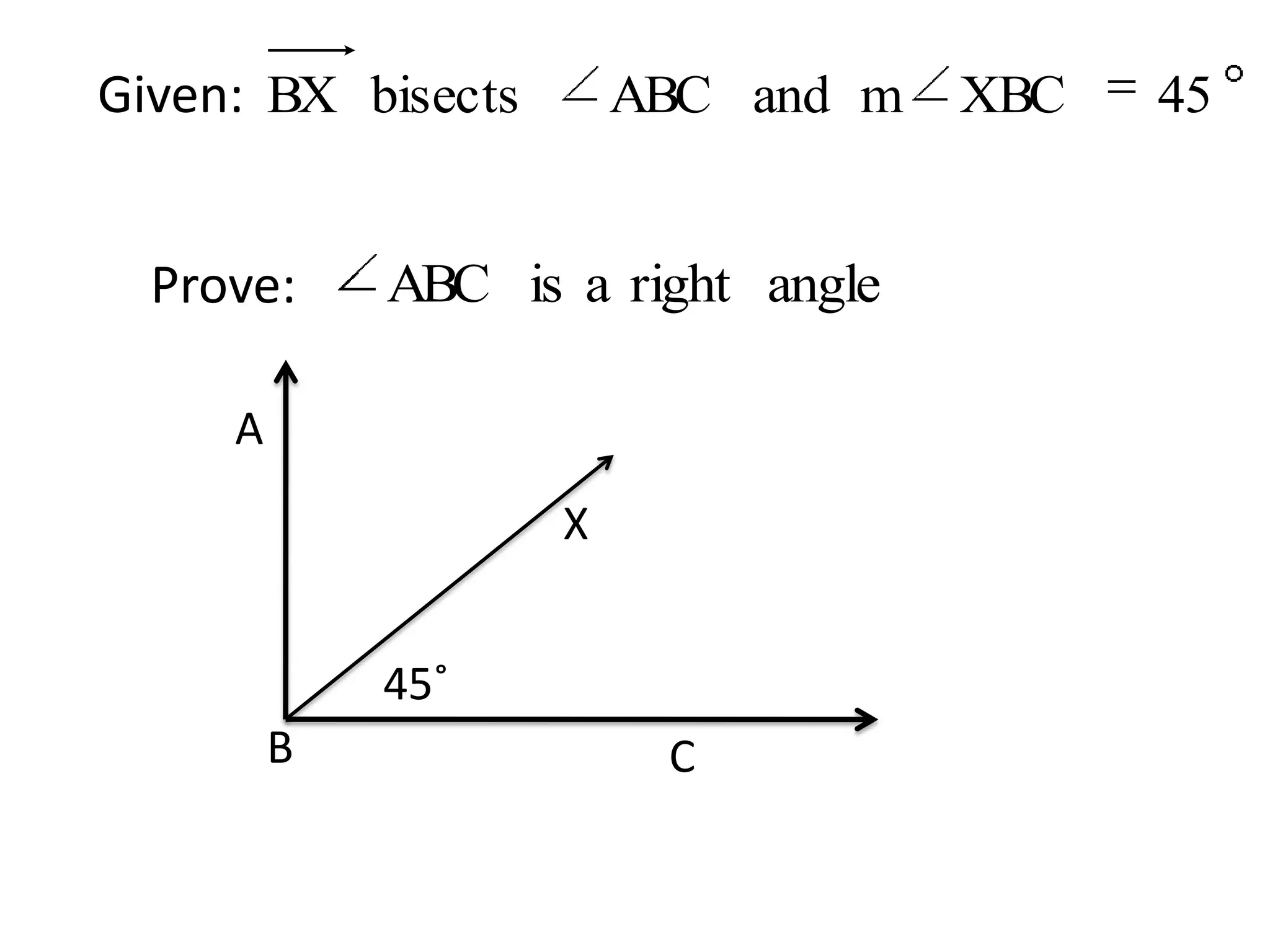
More complex statements and reasons in a proof scenario incorporating angle bisectors and congruency.
Further demonstration of 'Given' and 'Prove' framework within geometric proofs.
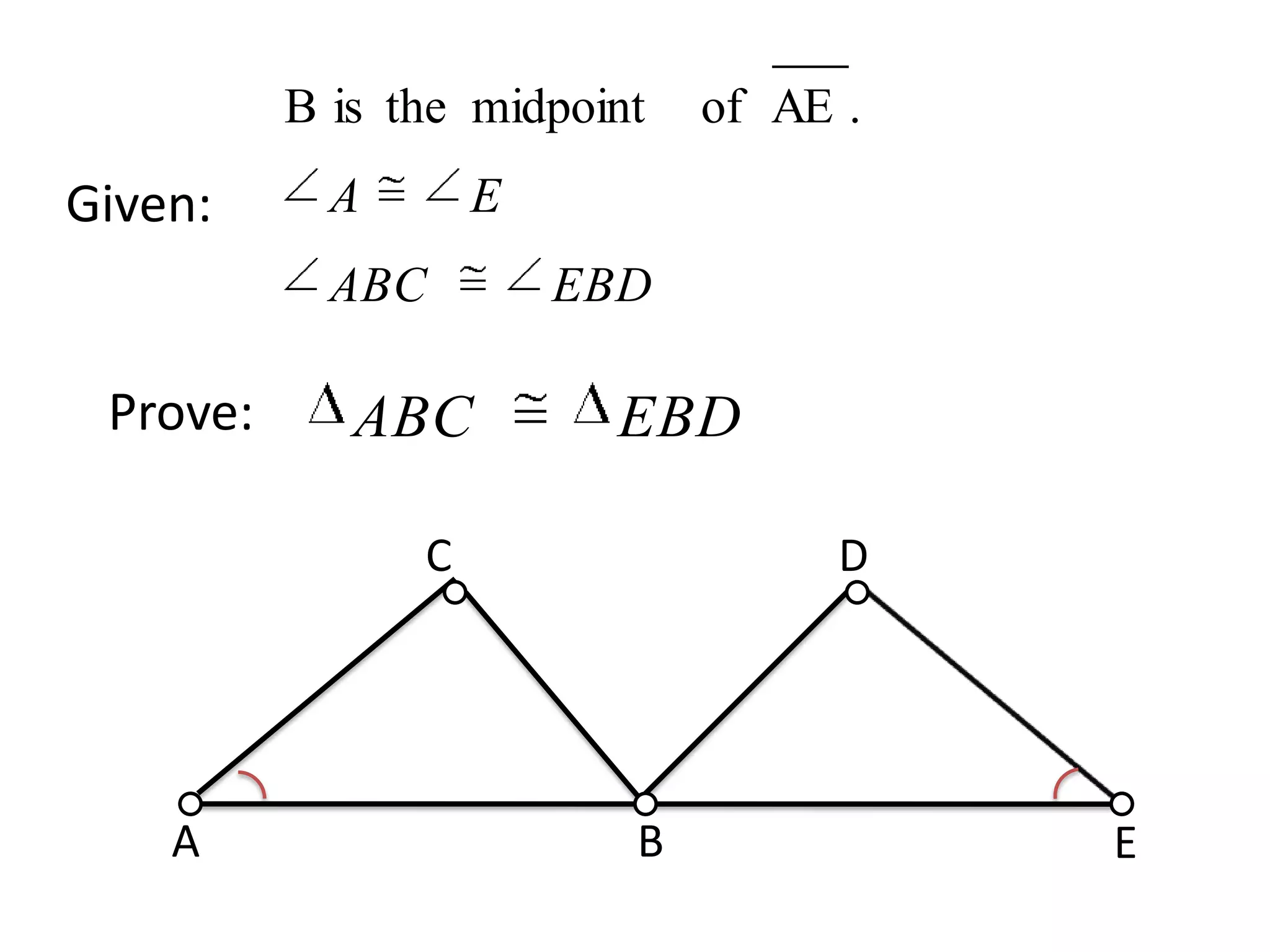
Example proof with defined statements and justifications including ASA criteria.
Another structured example showing 'Given' and 'Prove' segments in proof setup.
Showcase of advanced geometric proofs involving theorems such as Congruent Angles.
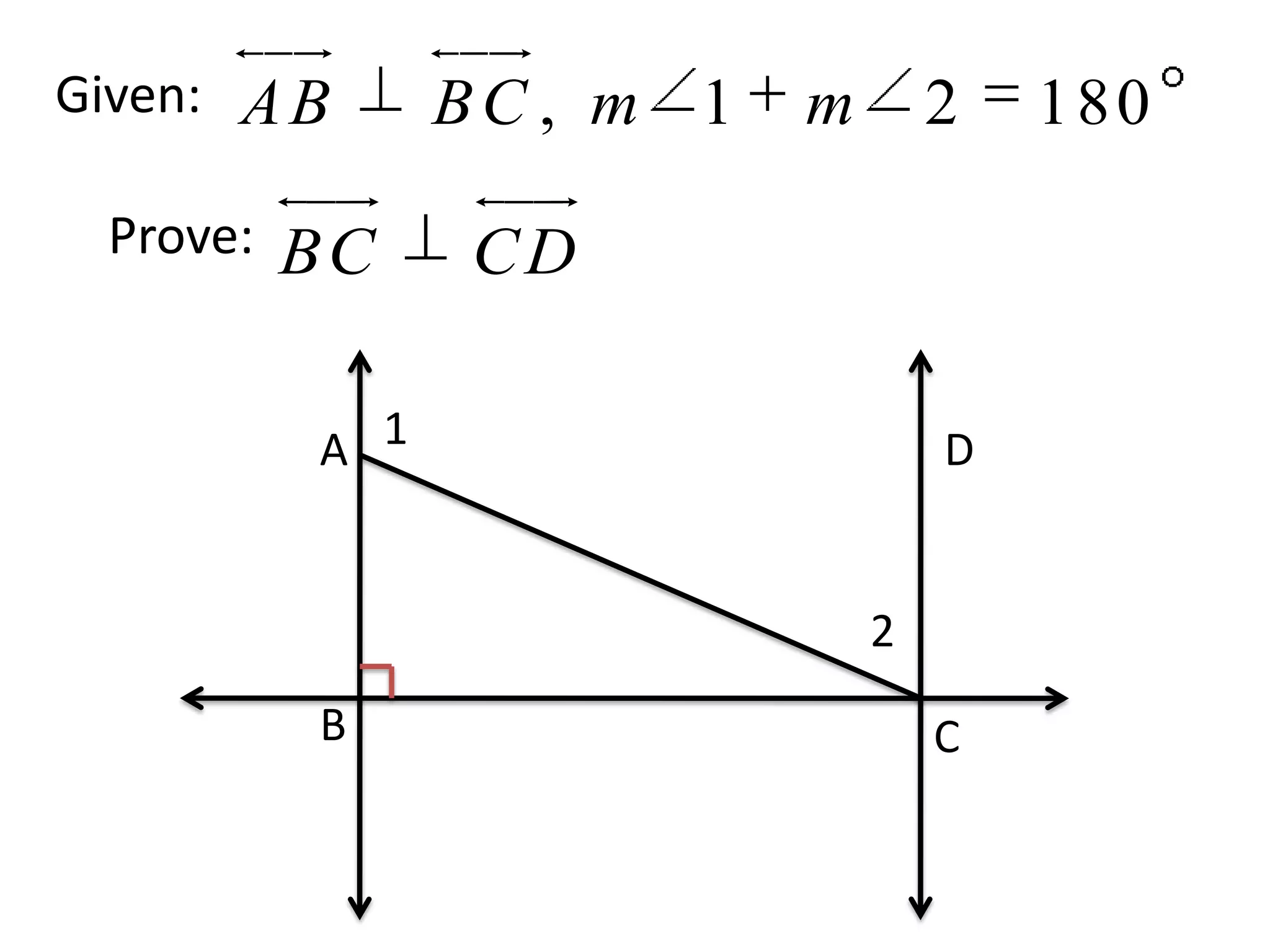
In-depth analysis of a proof scenario involving supplementary angles and their properties.
Continuation of detailed proof structure outlining the use of substitution properties and angles.
A complex proof setup showing the relationship among different geometric components.
Statement and reasoning format in segment analysis using properties relevant to proofs.
Completing the proof with defined parameters, further highlighting key definitions.
Finalization of statements and reasons integrated within a proof related to right angles.