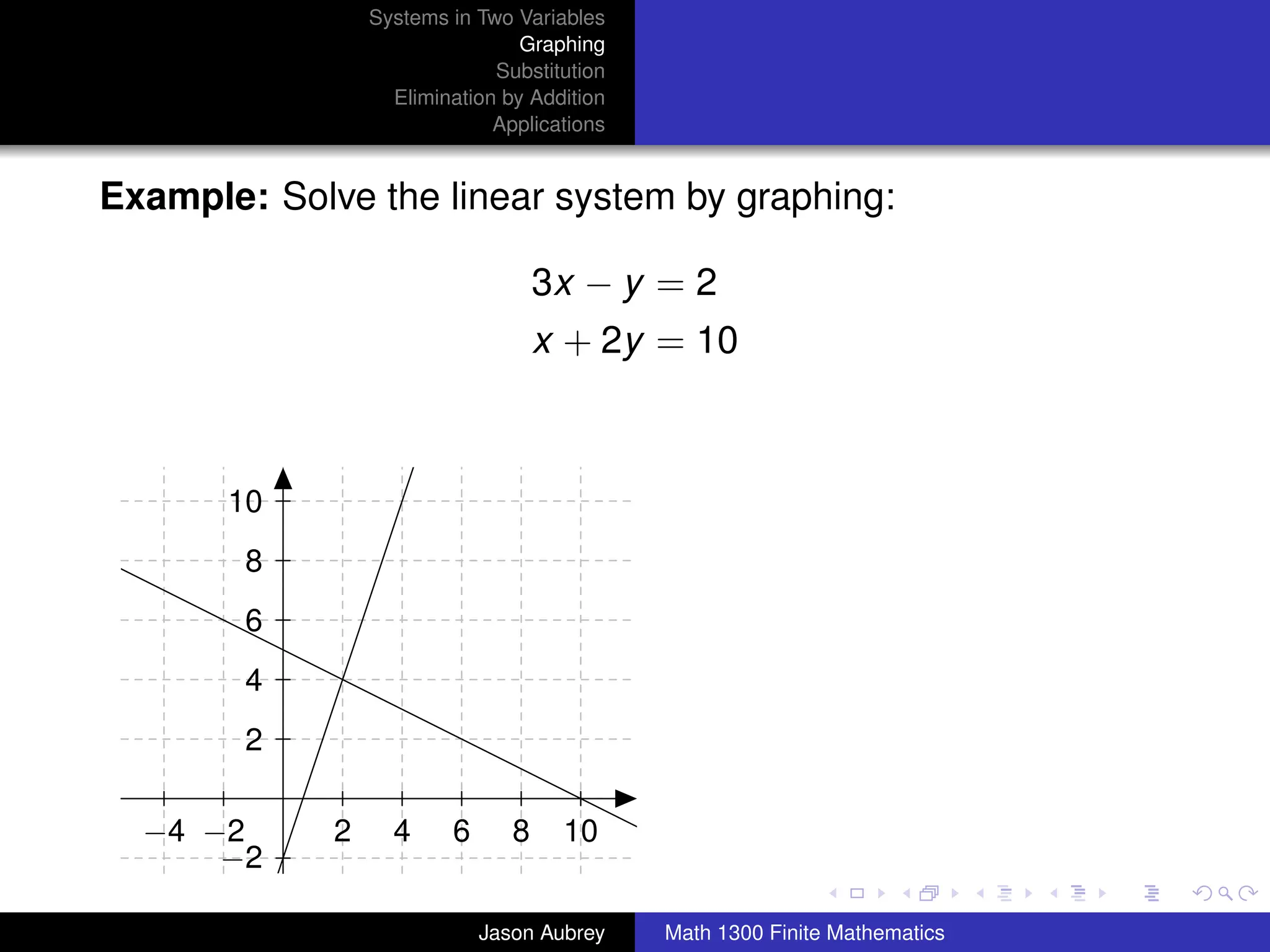
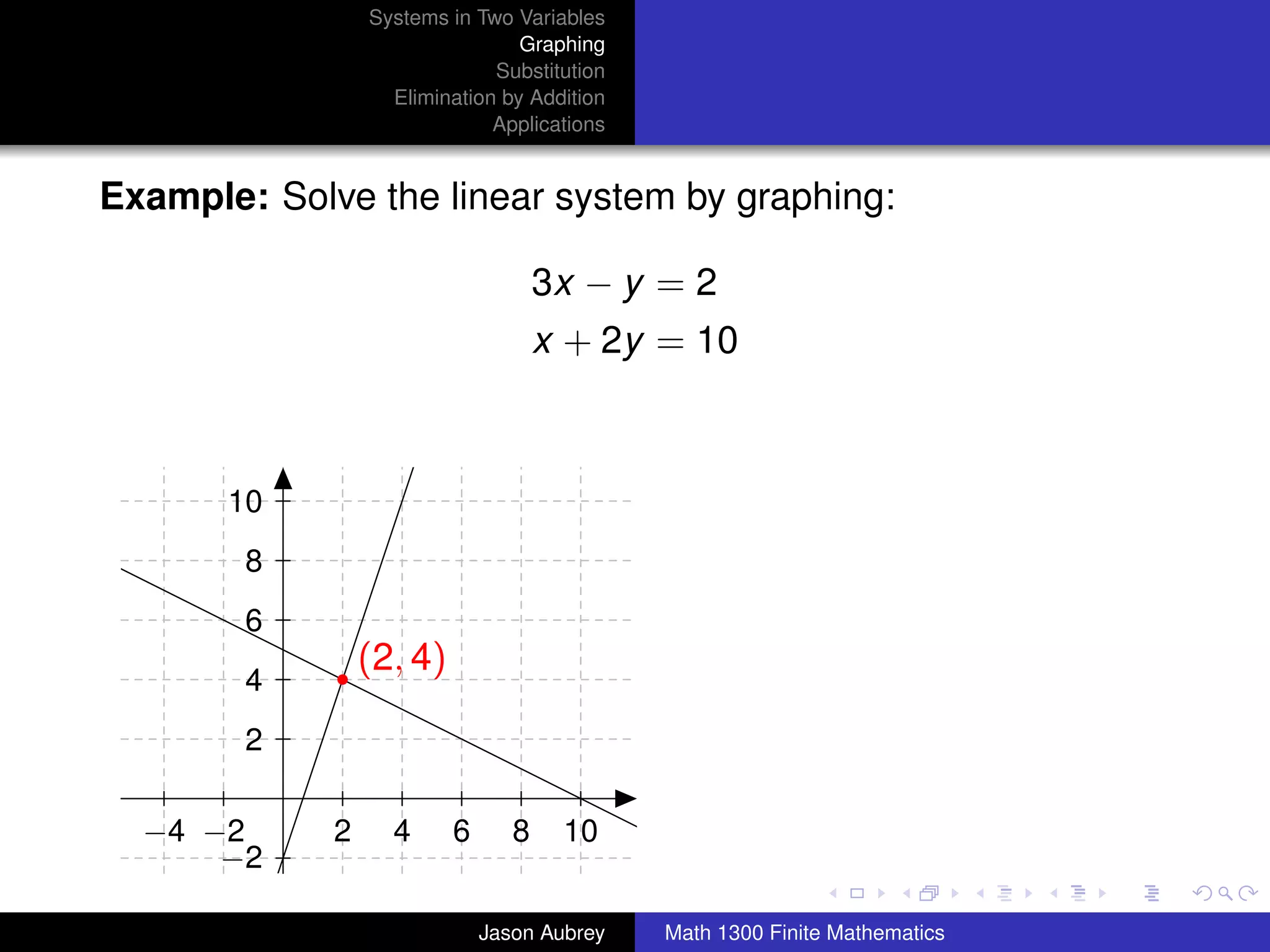
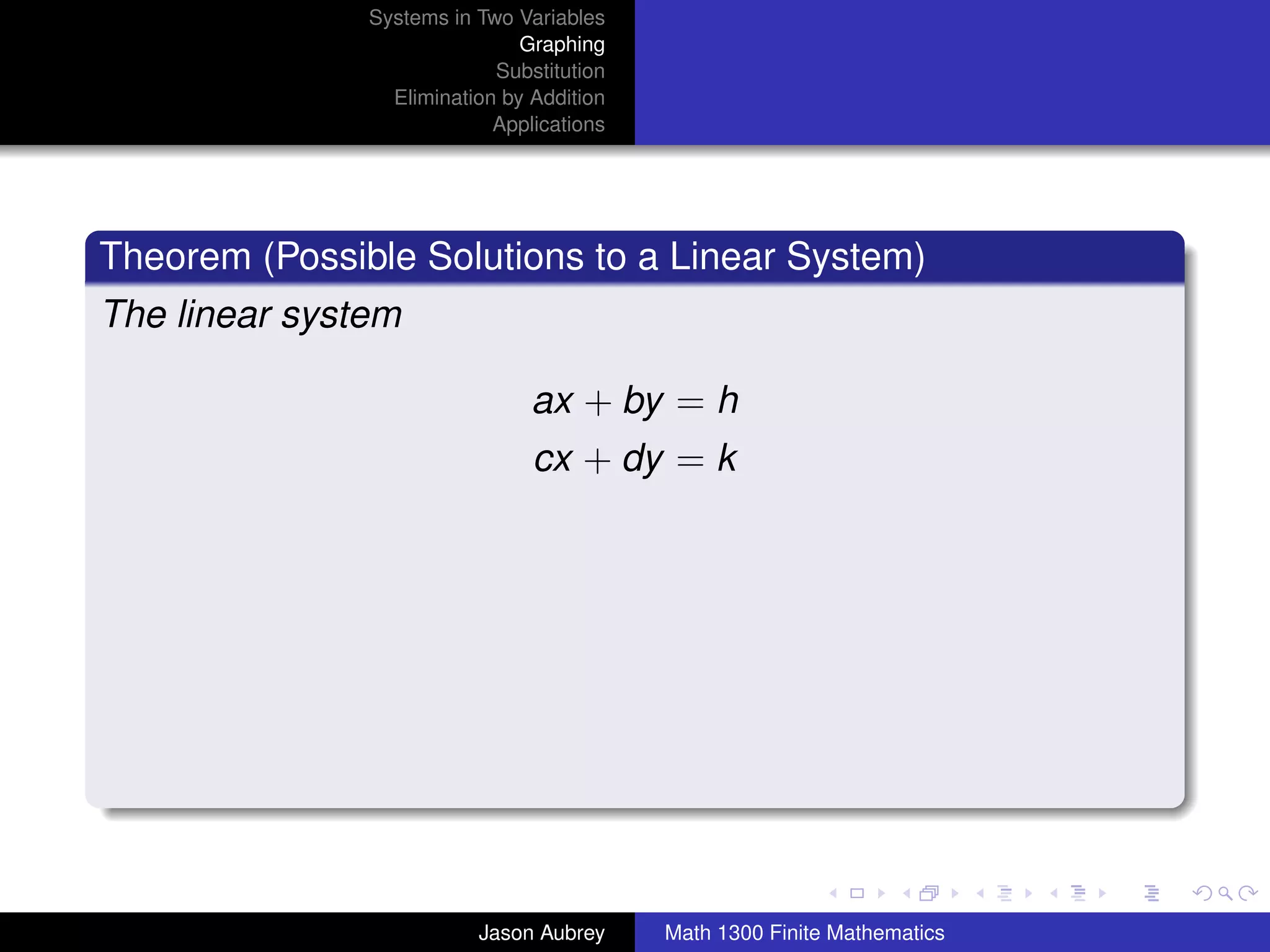
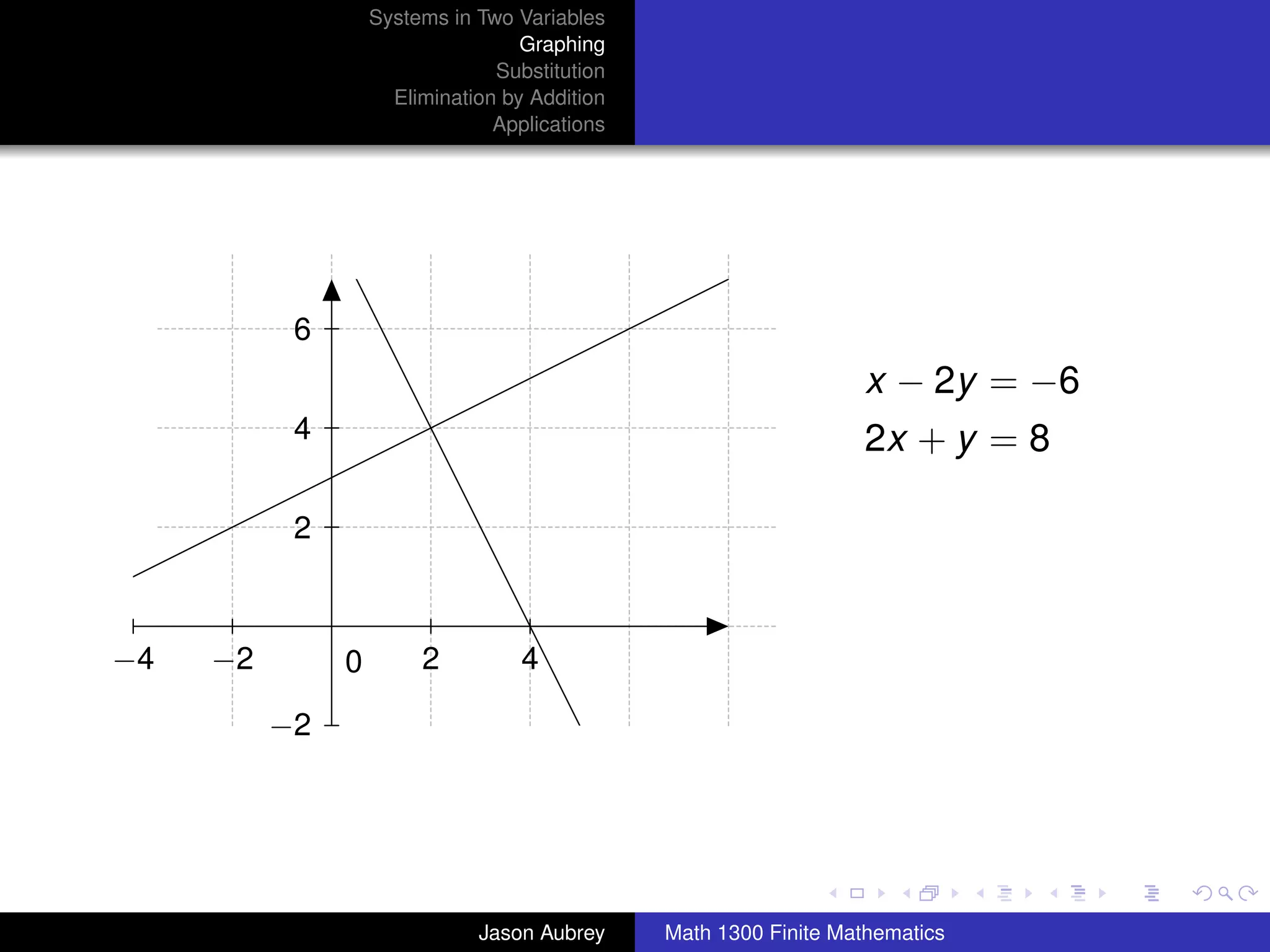
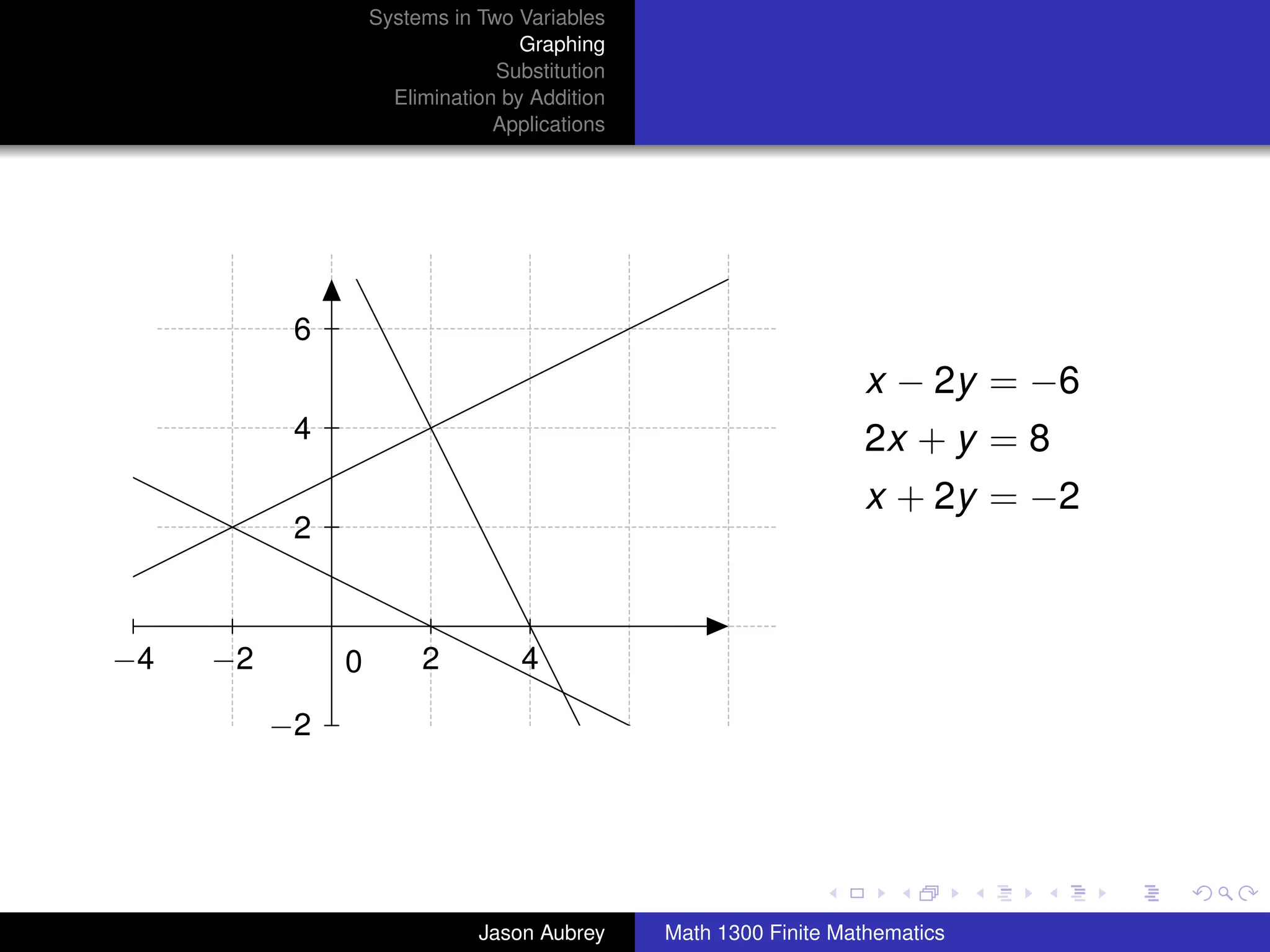
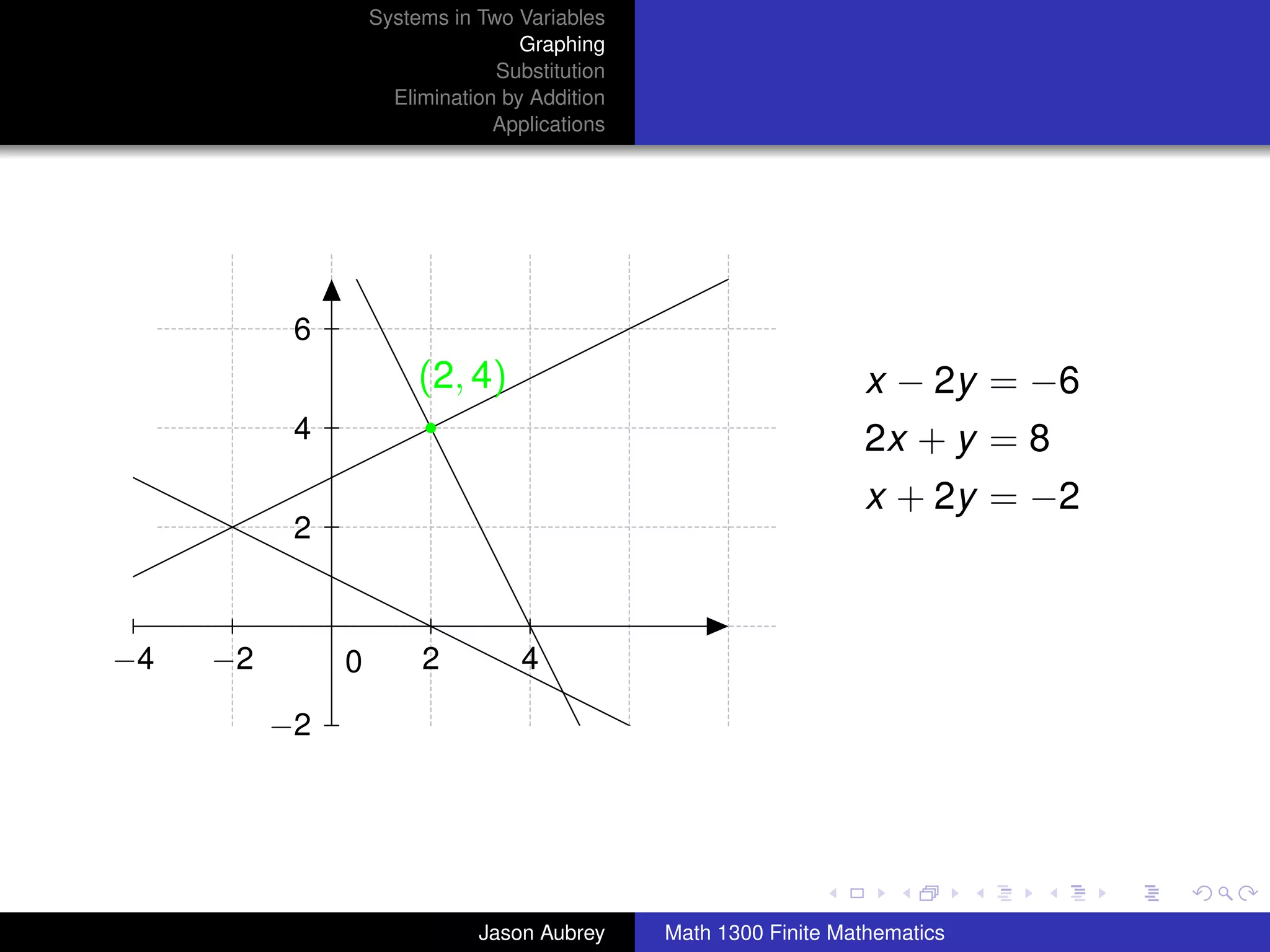
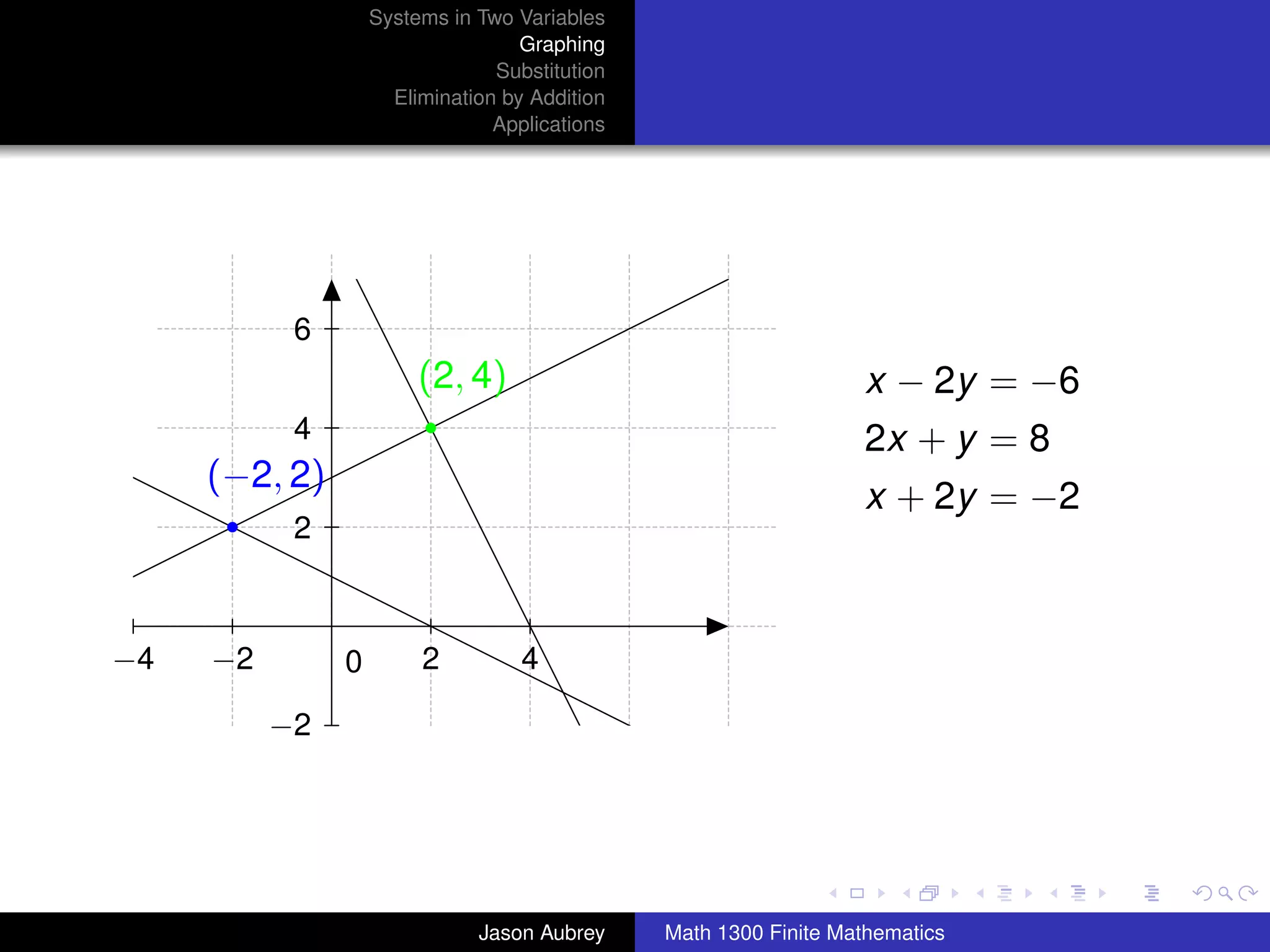
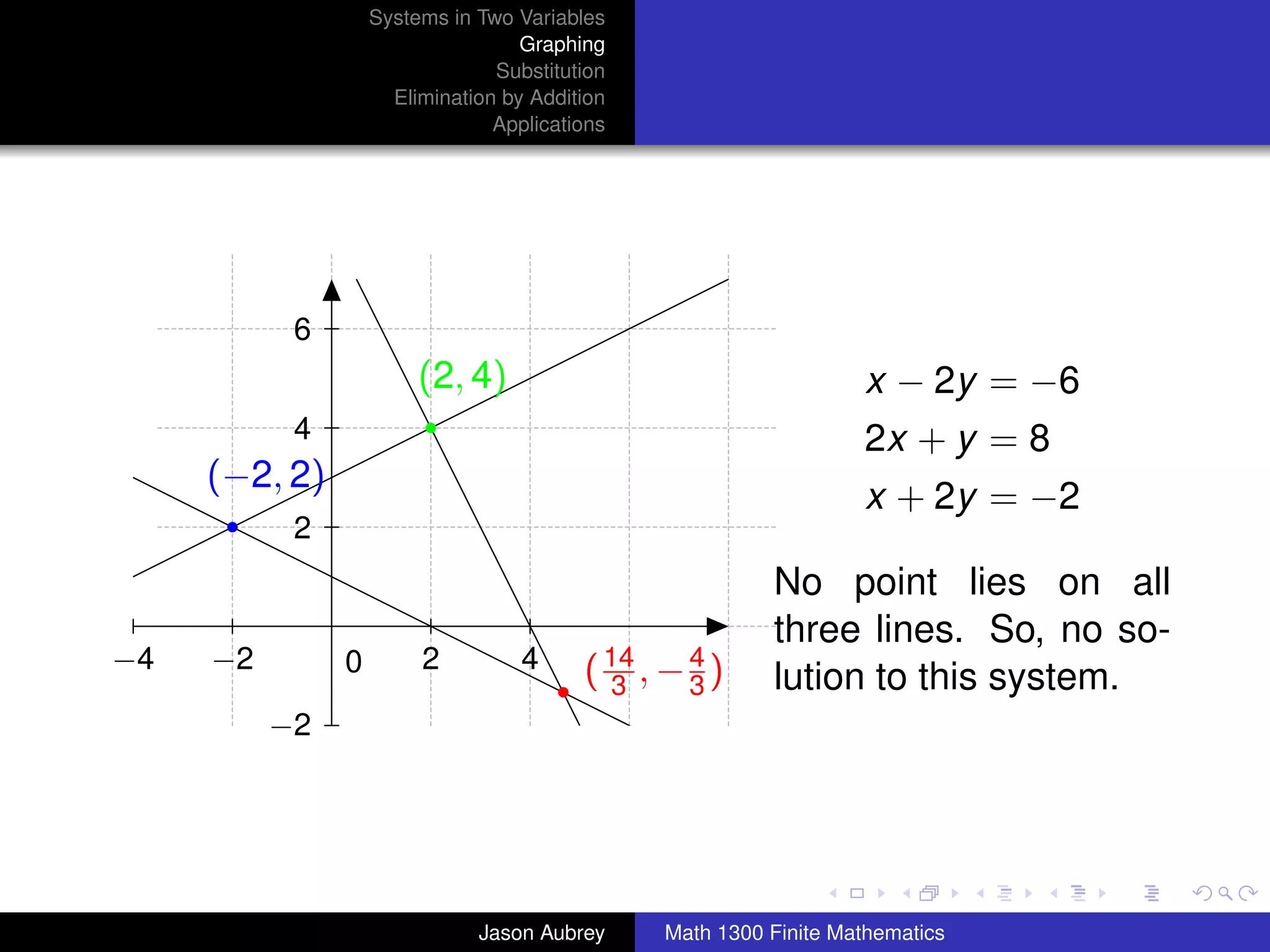
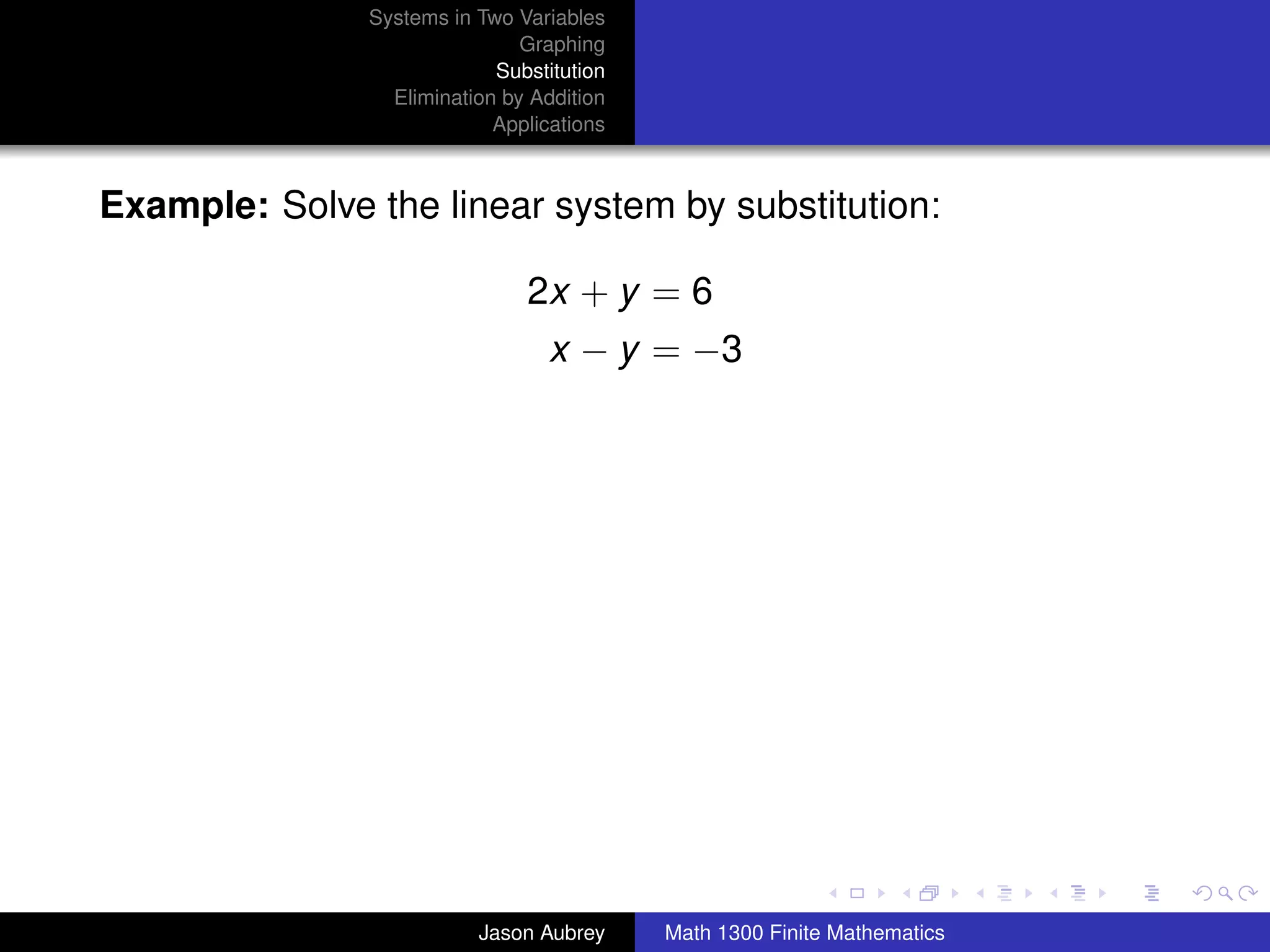
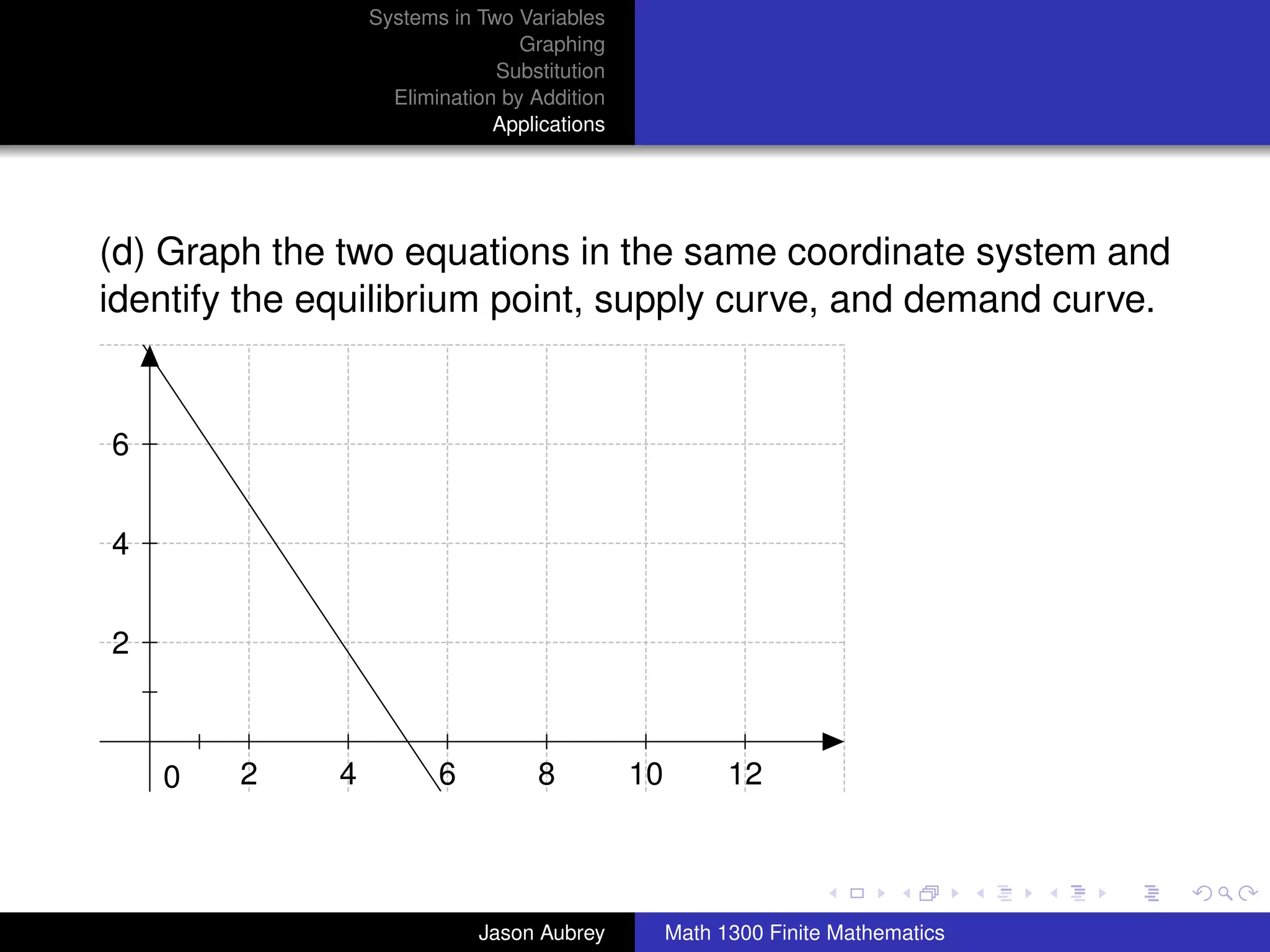
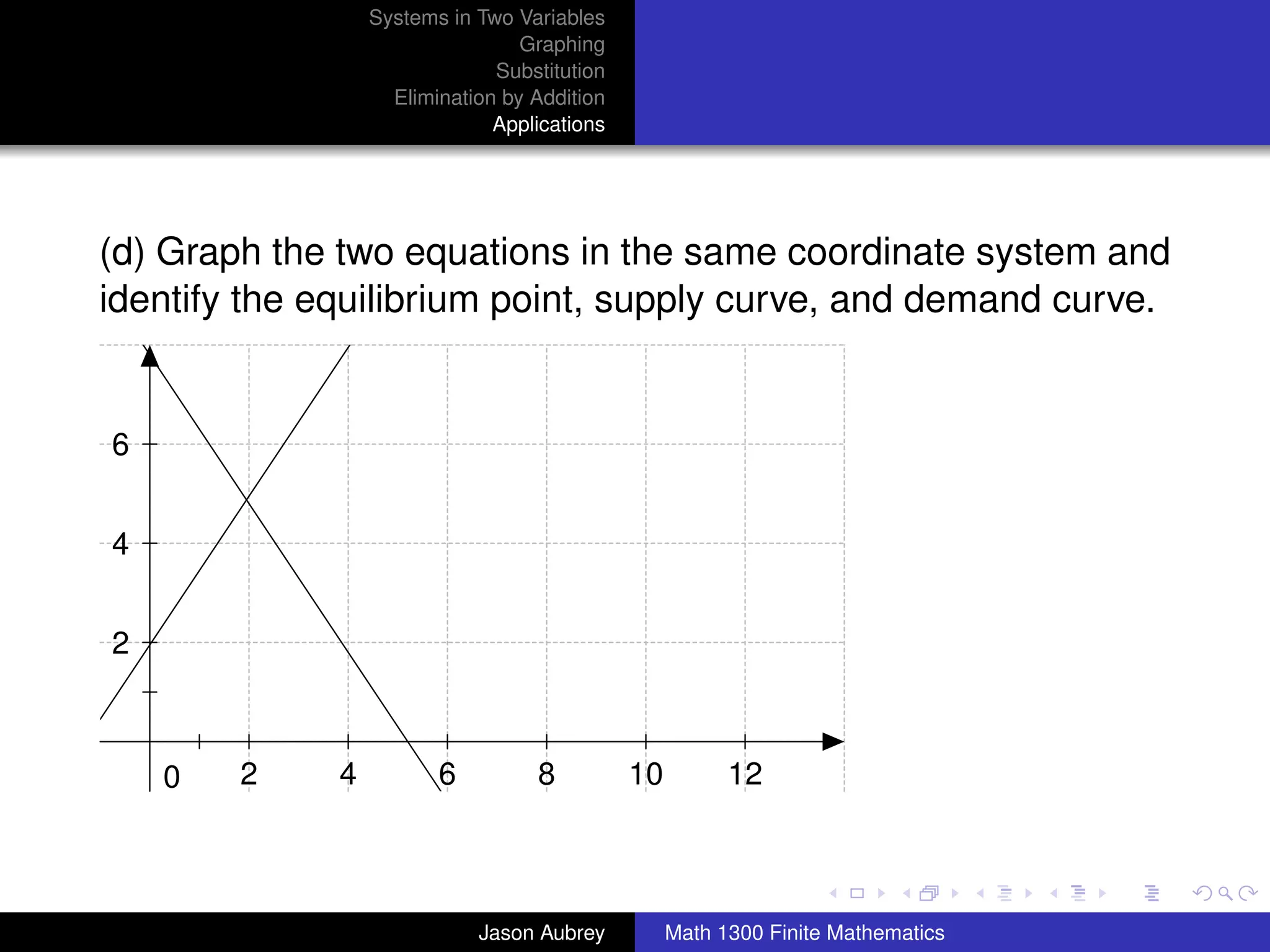
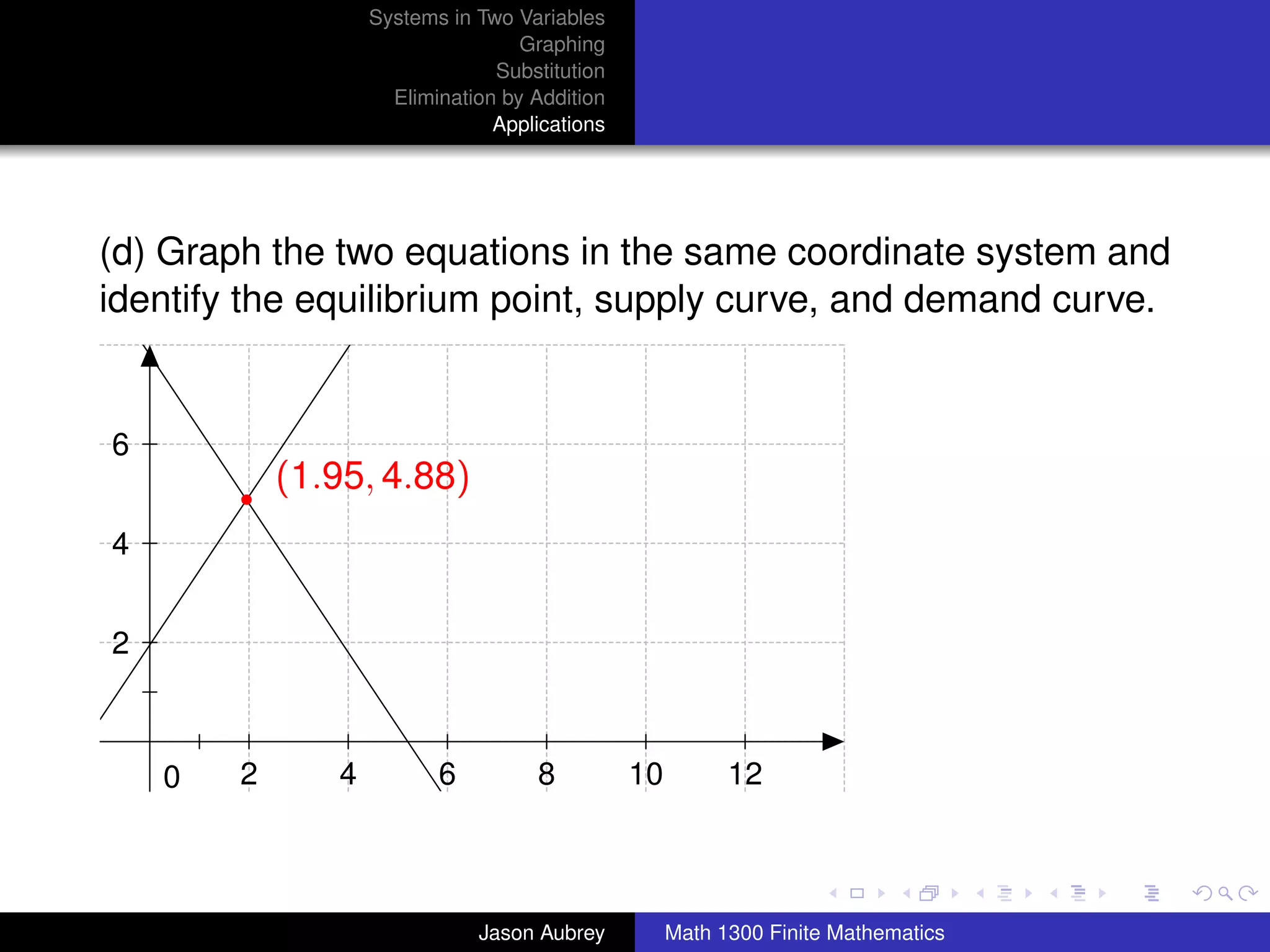
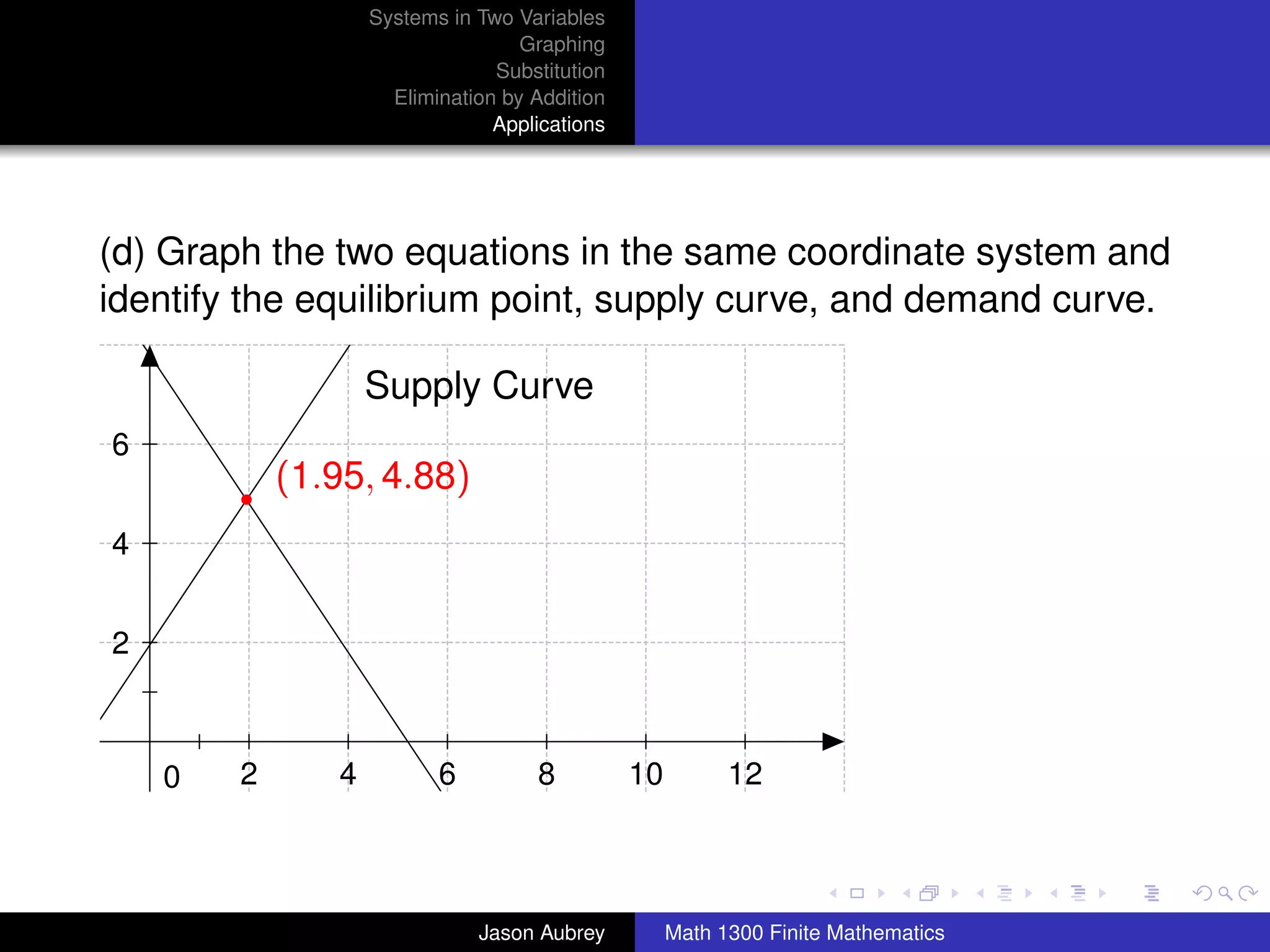
This document discusses solving systems of linear equations in two variables through three methods: graphing, substitution, and elimination. It defines key terms like consistent, independent, and dependent when describing systems of linear equations. The document also presents a theorem stating the possible solutions a linear system can have and provides an example of graphing a system to find the solution set.

1. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Math 1300 Finite Mathematics
Section 4.1 Review: Systems of Linear Equations in Two
Variables
Jason Aubrey
Department of Mathematics
University of Missouri
university-logo
Jason Aubrey Math 1300 Finite Mathematics

2. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Definition (Systems of Equations in Two Variables)
Given the linear system
ax + by = h
cx + dy = k
A pair of numbers x = x0 , y = y0 [also written as an ordered
pair (x0 , y0 ) is said to be a solution of the system if each
equation is satisfied by the pair. The set of all such ordered
pairs is called the solution set for the system. To solve a
system is to find its solution set.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

3. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Definition (Systems of Equations in Two Variables)
Given the linear system
ax + by = h
cx + dy = k
A pair of numbers x = x0 , y = y0 [also written as an ordered
pair (x0 , y0 ) is said to be a solution of the system if each
equation is satisfied by the pair. The set of all such ordered
pairs is called the solution set for the system. To solve a
system is to find its solution set.
We will consider three methods for solving such systems:
graphing, substitution, and elimination by addition. university-logo
Jason Aubrey Math 1300 Finite Mathematics

4. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by graphing:
3x − y = 2
x + 2y = 10
10
8
6
4
2
−4 −2 2 4 6 8 10 university-logo
−2
Jason Aubrey Math 1300 Finite Mathematics

5. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by graphing:
3x − y = 2
x + 2y = 10
10
8
6
4
2
−4 −2 2 4 6 8 10 university-logo
−2
Jason Aubrey Math 1300 Finite Mathematics

6. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by graphing:
3x − y = 2
x + 2y = 10
10
8
6
4
2
−4 −2 2 4 6 8 10 university-logo
−2
Jason Aubrey Math 1300 Finite Mathematics

7. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by graphing:
3x − y = 2
x + 2y = 10
10
8
6
(2, 4)
4
2
−4 −2 2 4 6 8 10 university-logo
−2
Jason Aubrey Math 1300 Finite Mathematics

8. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Definition (Systems of Linear Equations: Basic Terms)
A system of linear equations is consistent if it has one or more
solutions and inconsistent if no solutions exist. Furthermore, a
consistent system is said to be independent if it has exactly
one solution and dependent if it has more than one solution.
Two systems of equations are equivalent if they have the same
solution set.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

9. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Possible Solutions to a Linear System)
The linear system
ax + by = h
cx + dy = k
university-logo
Jason Aubrey Math 1300 Finite Mathematics

10. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Possible Solutions to a Linear System)
The linear system
ax + by = h
cx + dy = k
Must have
Exactly one solution (consistent and independent), or
university-logo
Jason Aubrey Math 1300 Finite Mathematics

11. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Possible Solutions to a Linear System)
The linear system
ax + by = h
cx + dy = k
Must have
Exactly one solution (consistent and independent), or
No solution (inconsistent), or
university-logo
Jason Aubrey Math 1300 Finite Mathematics

12. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Possible Solutions to a Linear System)
The linear system
ax + by = h
cx + dy = k
Must have
Exactly one solution (consistent and independent), or
No solution (inconsistent), or
Infinitely many solutions (consistent and dependent).
university-logo
Jason Aubrey Math 1300 Finite Mathematics

13. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Possible Solutions to a Linear System)
The linear system
ax + by = h
cx + dy = k
Must have
Exactly one solution (consistent and independent), or
No solution (inconsistent), or
Infinitely many solutions (consistent and dependent).
There are no other possibilities.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

14. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Graph the equations and find the coordinates of any
points where two or more lines intersect. Discuss the nature of
the solution set.
x − 2y = −6
2x + y = 8
x + 2y = −2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

15. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
4
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

16. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
x − 2y = −6
4
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

17. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
x − 2y = −6
4 2x + y = 8
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

18. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
x − 2y = −6
4 2x + y = 8
x + 2y = −2
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

19. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
(2, 4) x − 2y = −6
4 2x + y = 8
x + 2y = −2
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

20. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
(2, 4) x − 2y = −6
4 2x + y = 8
(−2, 2)
x + 2y = −2
2
−4 −2 0 2 4
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

21. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
6
(2, 4) x − 2y = −6
4 2x + y = 8
(−2, 2)
x + 2y = −2
2
No point lies on all
three lines. So, no so-
−4 −2 0 2 4 ( 14 , − 4 )
3 3 lution to this system.
−2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

22. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
university-logo
Jason Aubrey Math 1300 Finite Mathematics

23. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
university-logo
Jason Aubrey Math 1300 Finite Mathematics

24. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
university-logo
Jason Aubrey Math 1300 Finite Mathematics

25. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
x − y = −3
university-logo
Jason Aubrey Math 1300 Finite Mathematics

26. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
x − y = −3
x − (6 − 2x) = −3
university-logo
Jason Aubrey Math 1300 Finite Mathematics

27. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
x − y = −3
x − (6 − 2x) = −3
3x − 6 = −3
university-logo
Jason Aubrey Math 1300 Finite Mathematics

28. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
x − y = −3
x − (6 − 2x) = −3
3x − 6 = −3
x =1
university-logo
Jason Aubrey Math 1300 Finite Mathematics

29. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system by substitution:
2x + y = 6
x − y = −3
2x + y = 6
y = 6 − 2x now substitute:
x − y = −3
x − (6 − 2x) = −3
3x − 6 = −3
x =1
Substituting we obtain y = 4. So, the solution is the point (1, 4).
university-logo
Jason Aubrey Math 1300 Finite Mathematics

30. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Graphing and substitution work well for systems involving
two variables.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

31. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Graphing and substitution work well for systems involving
two variables.
However, neither is easily extended to larger systems.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

32. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Graphing and substitution work well for systems involving
two variables.
However, neither is easily extended to larger systems.
Elimination by addition is the most important method of
solution.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

33. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Graphing and substitution work well for systems involving
two variables.
However, neither is easily extended to larger systems.
Elimination by addition is the most important method of
solution.
It readily generalizes to larger systems and forms the basis
for computer-based solution methods.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

34. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Operations that Produce Equivalent Systems)
A system of linear equations is transformed into an equivalent
system if
university-logo
Jason Aubrey Math 1300 Finite Mathematics

35. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Operations that Produce Equivalent Systems)
A system of linear equations is transformed into an equivalent
system if
(A) Two equations are interchanged.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

36. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Operations that Produce Equivalent Systems)
A system of linear equations is transformed into an equivalent
system if
(A) Two equations are interchanged.
(B) An equation is multiplied by a nonzero constant.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

37. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Theorem (Operations that Produce Equivalent Systems)
A system of linear equations is transformed into an equivalent
system if
(A) Two equations are interchanged.
(B) An equation is multiplied by a nonzero constant.
(C) A constant multiple of one equation is added to another
equation.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

38. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
university-logo
Jason Aubrey Math 1300 Finite Mathematics

39. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
3u − 2v = 12
university-logo
Jason Aubrey Math 1300 Finite Mathematics

40. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
3u − 2v = 12
+7u + 2v = 8
university-logo
Jason Aubrey Math 1300 Finite Mathematics

41. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
3u − 2v = 12
+7u + 2v = 8
10u + 0 = 20
university-logo
Jason Aubrey Math 1300 Finite Mathematics

42. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
3u − 2v = 12
+7u + 2v = 8
10u + 0 = 20
u=2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

43. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve the linear system using elimination by addition
3u − 2v = 12
7u + 2v = 8
3u − 2v = 12
+7u + 2v = 8
10u + 0 = 20
u=2
Substituting, we obtain v = −3. So the solution is (2,-3)
university-logo
Jason Aubrey Math 1300 Finite Mathematics

44. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
university-logo
Jason Aubrey Math 1300 Finite Mathematics

45. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

46. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
15x − 10y = 40
university-logo
Jason Aubrey Math 1300 Finite Mathematics

47. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
15x − 10y = 40
4x + 10y = −2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

48. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
15x − 10y = 40
4x + 10y = −2
19x = 38
university-logo
Jason Aubrey Math 1300 Finite Mathematics

49. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
15x − 10y = 40
4x + 10y = −2
19x = 38
1
Now we multiply both sides of this last equation by 19 to obtain
x = 2.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

50. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: Solve using elimination by addition.
3x − 2y = 8
2x + 5y = −1
We multiply the first equation by 5 and the bottom equation by 2
and then add.
15x − 10y = 40
4x + 10y = −2
19x = 38
1
Now we multiply both sides of this last equation by 19 to obtain
x = 2. Then we substitute back into either of the two original
equations to obtain y = −1. university-logo
Jason Aubrey Math 1300 Finite Mathematics

51. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Example: At $4.80 per bushel, the annual supply for soybeans
in the Midwest is 1.9 billion bushels and the annual demand is
2.0 billion bushels. When the price increases to $5.10 per
bushel, the annual supply increases to 2.1 billion bushels and
the annual demand decreases to 1.8 billion bushels. Assume
that the supply and demand equations are linear.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

52. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(a) Find the supply equation.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

53. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(a) Find the supply equation.
We wish to find an equation of the form p = mq + b where p
represents unit price and q represents quantity demanded.
We have two points (q, p) on the graph of the supply equation:
(1.9, 4.80) and (2.1, 5.10).
university-logo
Jason Aubrey Math 1300 Finite Mathematics

54. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(a) Find the supply equation.
We wish to find an equation of the form p = mq + b where p
represents unit price and q represents quantity demanded.
We have two points (q, p) on the graph of the supply equation:
(1.9, 4.80) and (2.1, 5.10).
The slope of this line is:
university-logo
Jason Aubrey Math 1300 Finite Mathematics

55. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(a) Find the supply equation.
We wish to find an equation of the form p = mq + b where p
represents unit price and q represents quantity demanded.
We have two points (q, p) on the graph of the supply equation:
(1.9, 4.80) and (2.1, 5.10).
The slope of this line is:
5.10 − 4.80 0.3 3
m= = =
2.1 − 1.9 0.2 2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

56. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Therefore the equation of this line is
university-logo
Jason Aubrey Math 1300 Finite Mathematics

57. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Therefore the equation of this line is
3
p − 4.8 = (q − 1.9)
2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

58. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Therefore the equation of this line is
3
p − 4.8 = (q − 1.9)
2
3 3
p = q − (1.9) + 4.8
2 2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

59. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
Therefore the equation of this line is
3
p − 4.8 = (q − 1.9)
2
3 3
p = q − (1.9) + 4.8
2 2
3
p = q + 1.95
2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

60. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

61. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
Again, we want an equation of the form p = mq + b. We have
two points on the graph of the demand equation: (2.0, 4.80)
and (1.8, 5.10).
university-logo
Jason Aubrey Math 1300 Finite Mathematics

62. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
Again, we want an equation of the form p = mq + b. We have
two points on the graph of the demand equation: (2.0, 4.80)
and (1.8, 5.10).
The slope of this line is:
5.10 − 4.80 0.3 3
m= =− =−
1.8 − 2.0 0.2 2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

63. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
Again, we want an equation of the form p = mq + b. We have
two points on the graph of the demand equation: (2.0, 4.80)
and (1.8, 5.10).
The slope of this line is:
5.10 − 4.80 0.3 3
m= =− =−
1.8 − 2.0 0.2 2
Therefore the equation of this line is
3
p − 4.80 = − (q − 2.0)
2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

64. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
Again, we want an equation of the form p = mq + b. We have
two points on the graph of the demand equation: (2.0, 4.80)
and (1.8, 5.10).
The slope of this line is:
5.10 − 4.80 0.3 3
m= =− =−
1.8 − 2.0 0.2 2
Therefore the equation of this line is
3
p − 4.80 = − (q − 2.0)
2
3 3
p = − q + (2.0) + 4.80
2 2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

65. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(b) Find the demand equation.
Again, we want an equation of the form p = mq + b. We have
two points on the graph of the demand equation: (2.0, 4.80)
and (1.8, 5.10).
The slope of this line is:
5.10 − 4.80 0.3 3
m= =− =−
1.8 − 2.0 0.2 2
Therefore the equation of this line is
3
p − 4.80 = − (q − 2.0)
2
3 3
p = − q + (2.0) + 4.80
2 2
3
p = − q + 7.80 university-logo
2
Jason Aubrey Math 1300 Finite Mathematics

66. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(c) Find the equilibrium price and quantity.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

67. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(c) Find the equilibrium price and quantity.
We set supply equal to demand and solve:
3 3
− q + 7.80 = q + 1.95
2 2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

68. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(c) Find the equilibrium price and quantity.
We set supply equal to demand and solve:
3 3
− q + 7.80 = q + 1.95
2 2
3q = 5.85
university-logo
Jason Aubrey Math 1300 Finite Mathematics

69. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(c) Find the equilibrium price and quantity.
We set supply equal to demand and solve:
3 3
− q + 7.80 = q + 1.95
2 2
3q = 5.85
q = 1.95 billion bushels
university-logo
Jason Aubrey Math 1300 Finite Mathematics

70. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(c) Find the equilibrium price and quantity.
We set supply equal to demand and solve:
3 3
− q + 7.80 = q + 1.95
2 2
3q = 5.85
q = 1.95 billion bushels
Substituting, we find p = − 3 (1.95) + 7.80 = $4.88
2
university-logo
Jason Aubrey Math 1300 Finite Mathematics

71. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
university-logo
Jason Aubrey Math 1300 Finite Mathematics

72. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
f
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
6
4
2
0 2 4 6 8 10 12
university-logo
Jason Aubrey Math 1300 Finite Mathematics

73. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
f
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
6
4
2
0 2 4 6 8 10 12
g
university-logo
Jason Aubrey Math 1300 Finite Mathematics

74. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
f
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
6
(1.95, 4.88)
4
2
0 2 4 6 8 10 12
g
university-logo
Jason Aubrey Math 1300 Finite Mathematics

75. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
f
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
Supply Curve
6
(1.95, 4.88)
4
2
0 2 4 6 8 10 12
g
university-logo
Jason Aubrey Math 1300 Finite Mathematics

76. Systems in Two Variables
Graphing
Substitution
Elimination by Addition
Applications
f
(d) Graph the two equations in the same coordinate system and
identify the equilibrium point, supply curve, and demand curve.
Supply Curve
6
(1.95, 4.88)
4
2 Demand Curve
0 2 4 6 8 10 12
g
university-logo
Jason Aubrey Math 1300 Finite Mathematics