The document discusses present value calculations for annuities and amortization schedules. It provides the formula to calculate the present value of an ordinary annuity. It then works through two examples, one calculating the present value needed to fund annual withdrawals over 20 years, and the other calculating the monthly payment for a $50,000, 20-year mortgage at 7.2% interest compounded monthly.
















































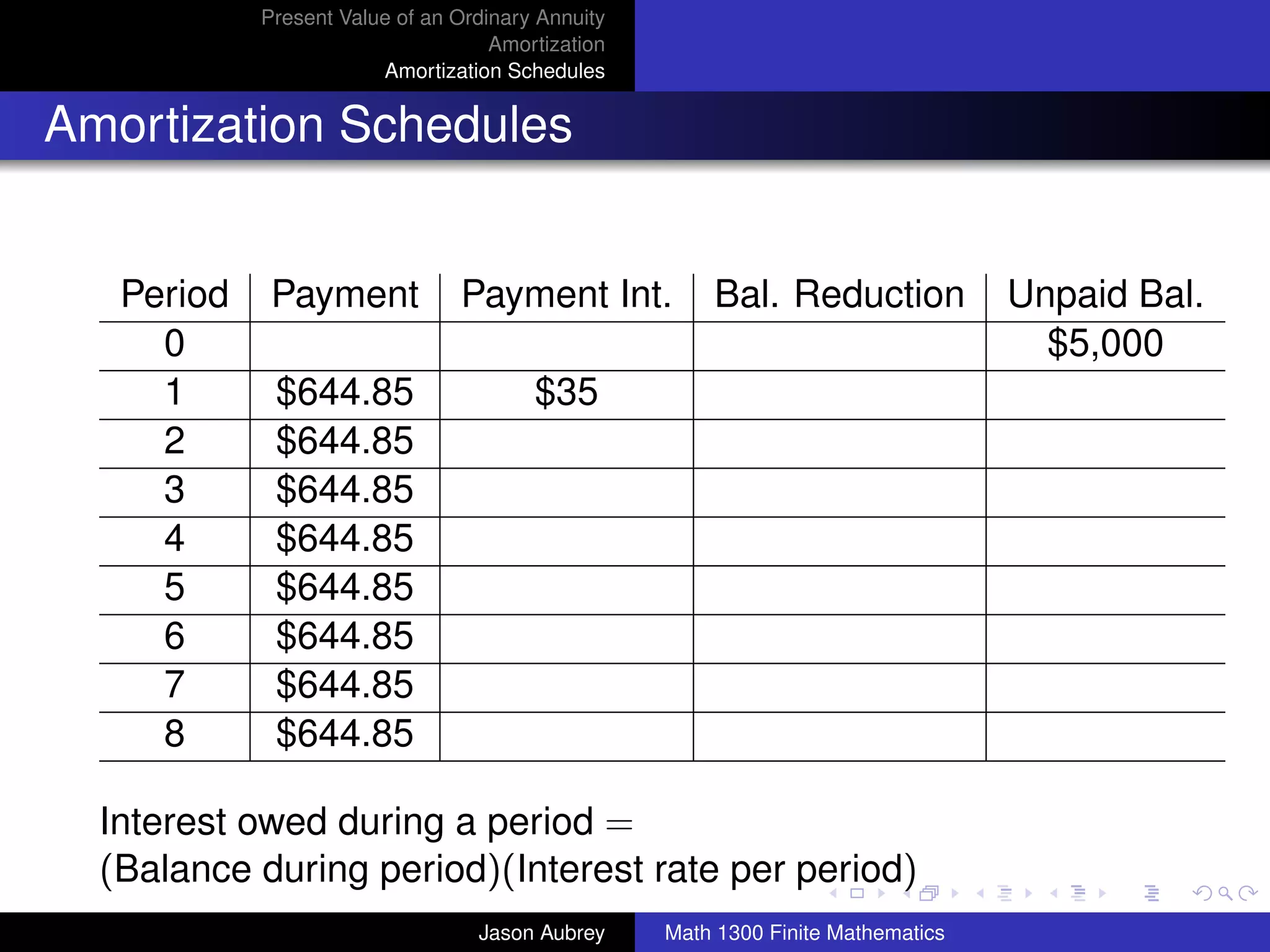
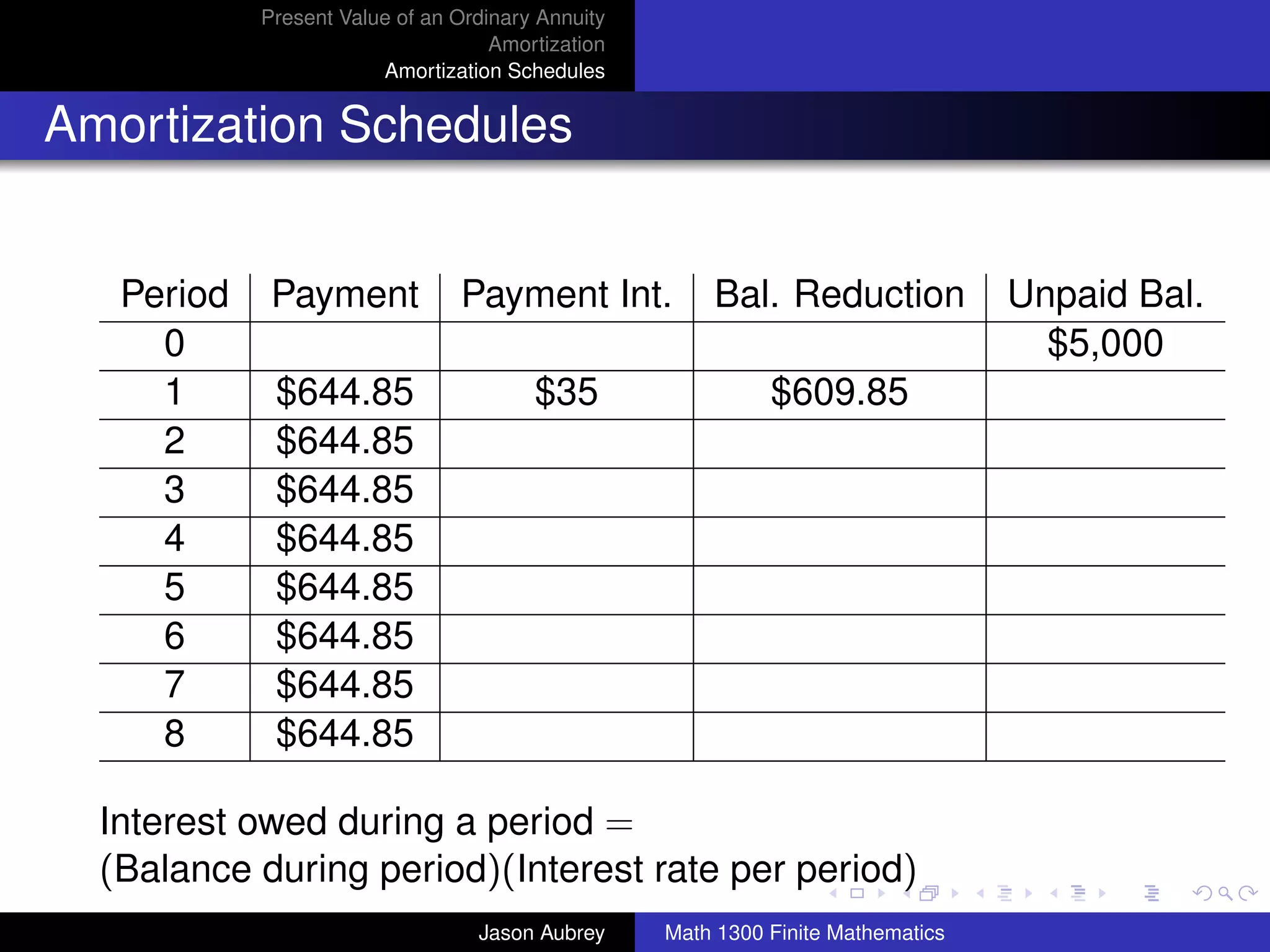
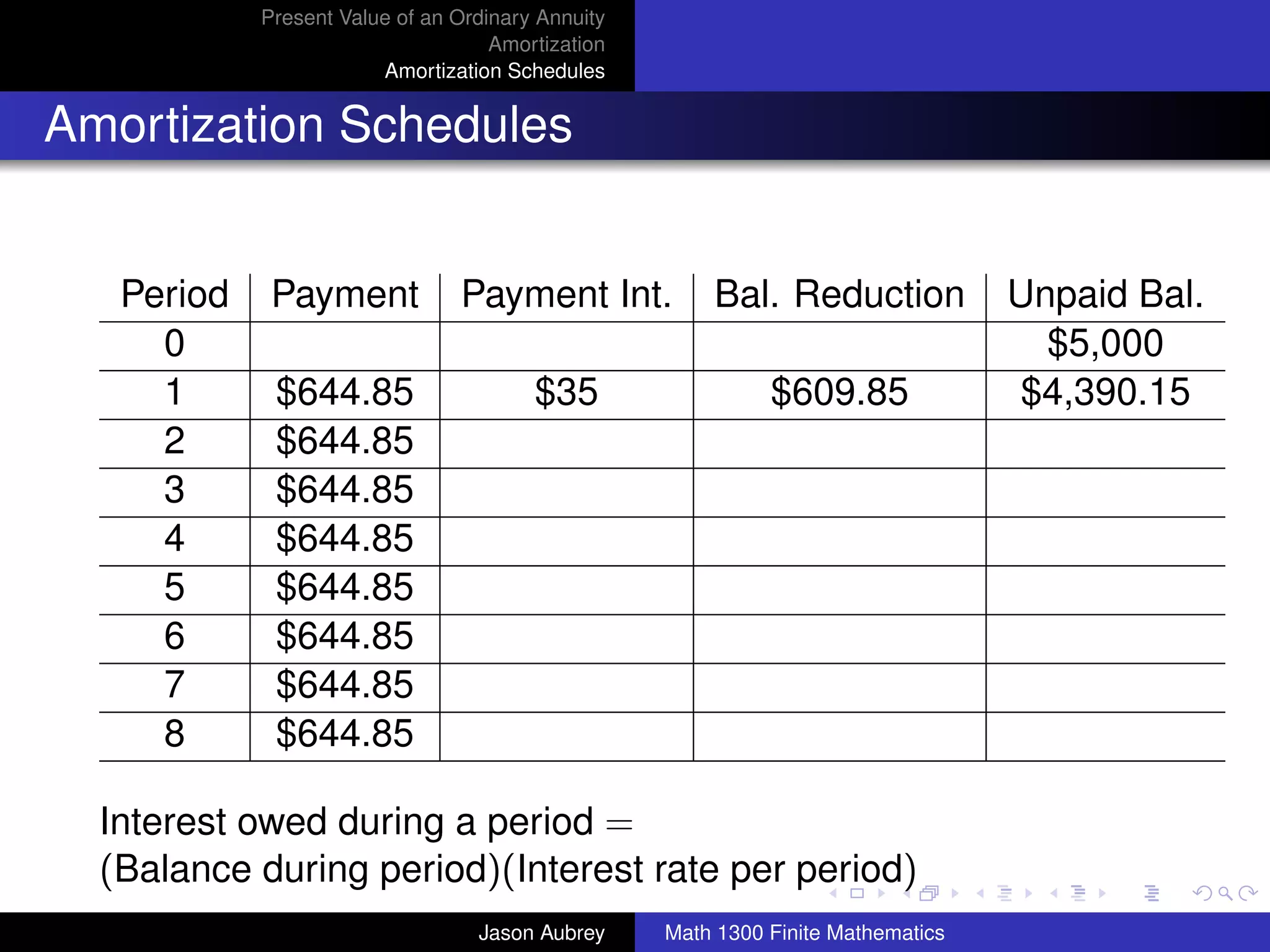
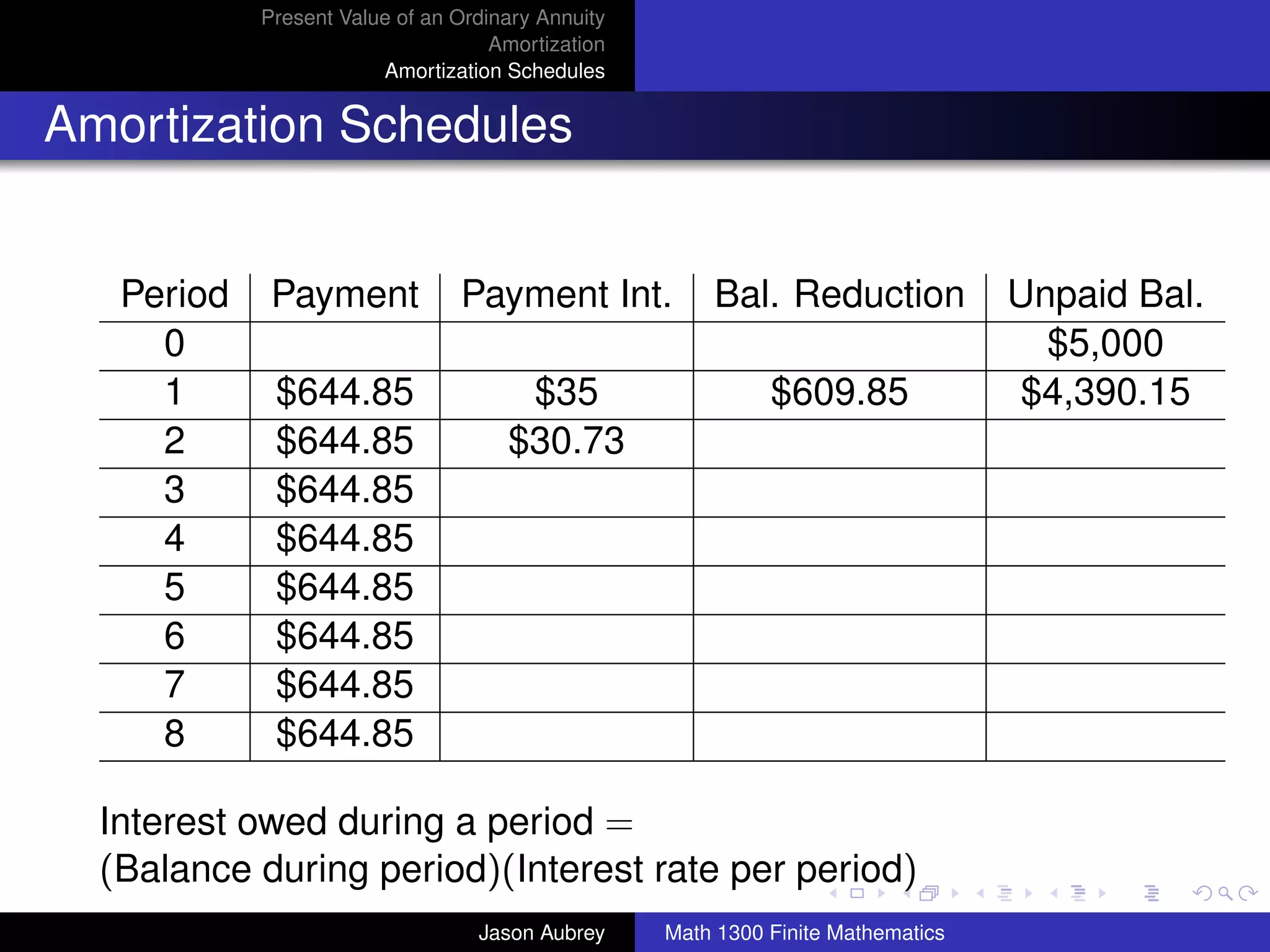
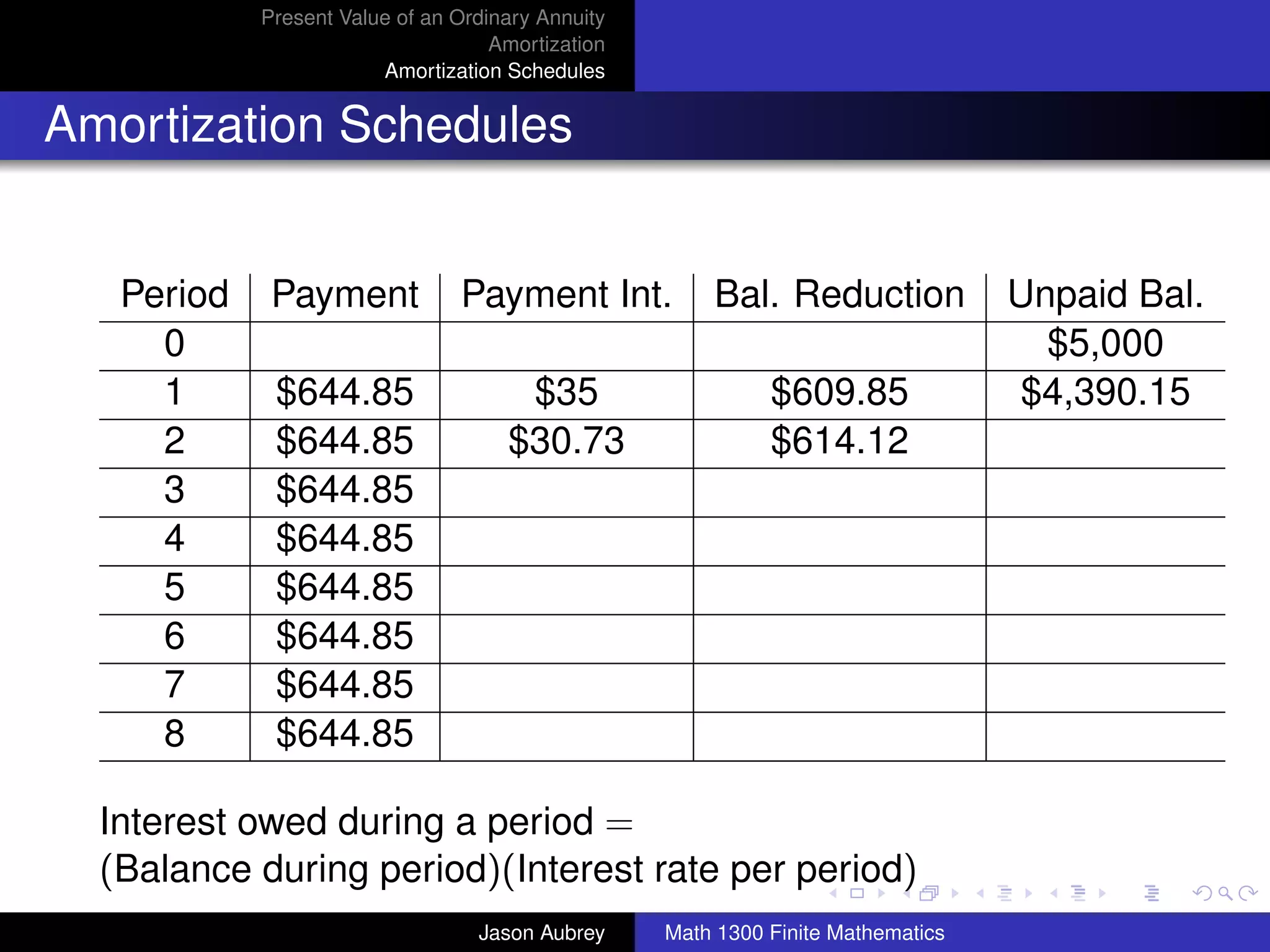
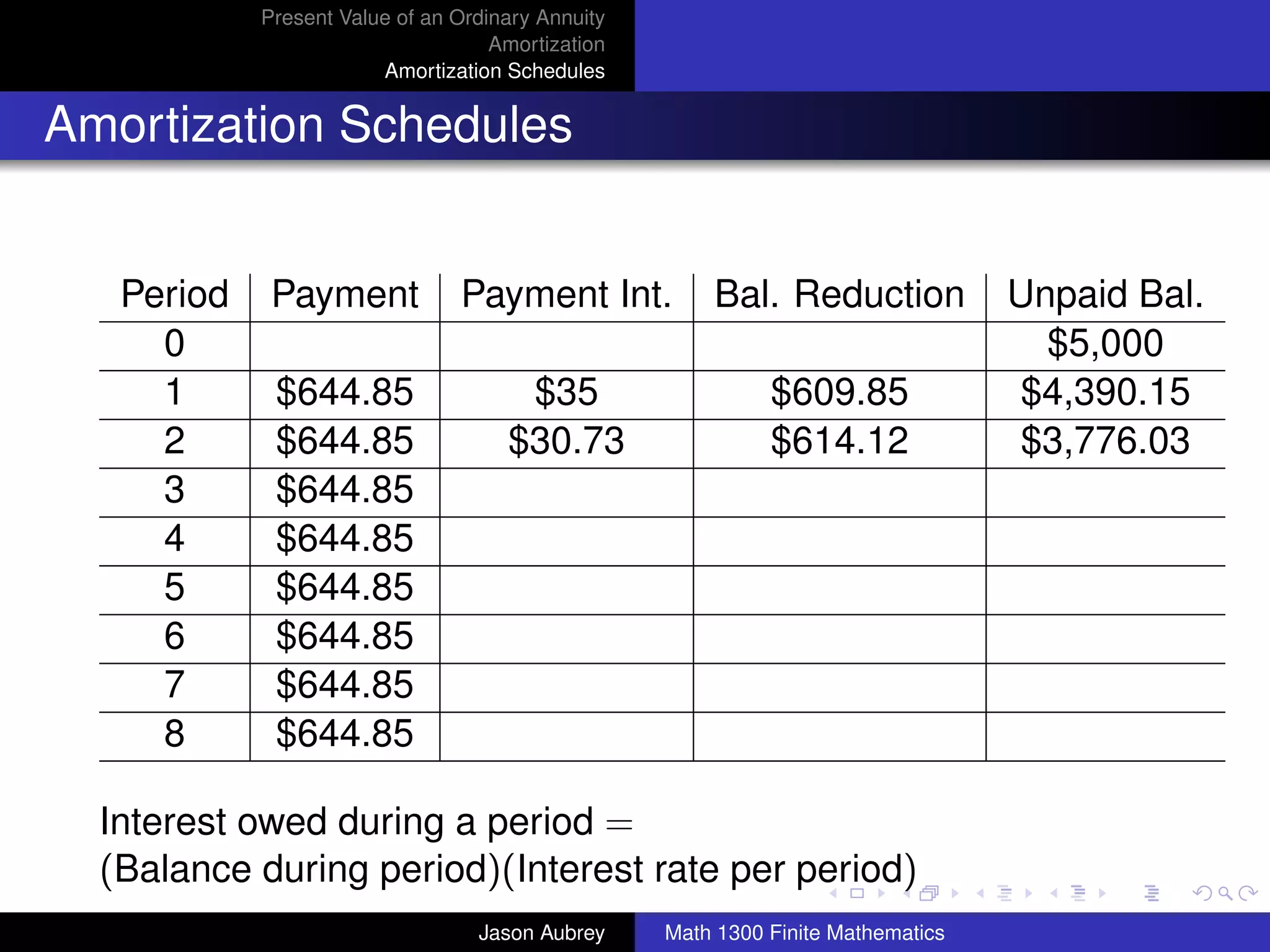
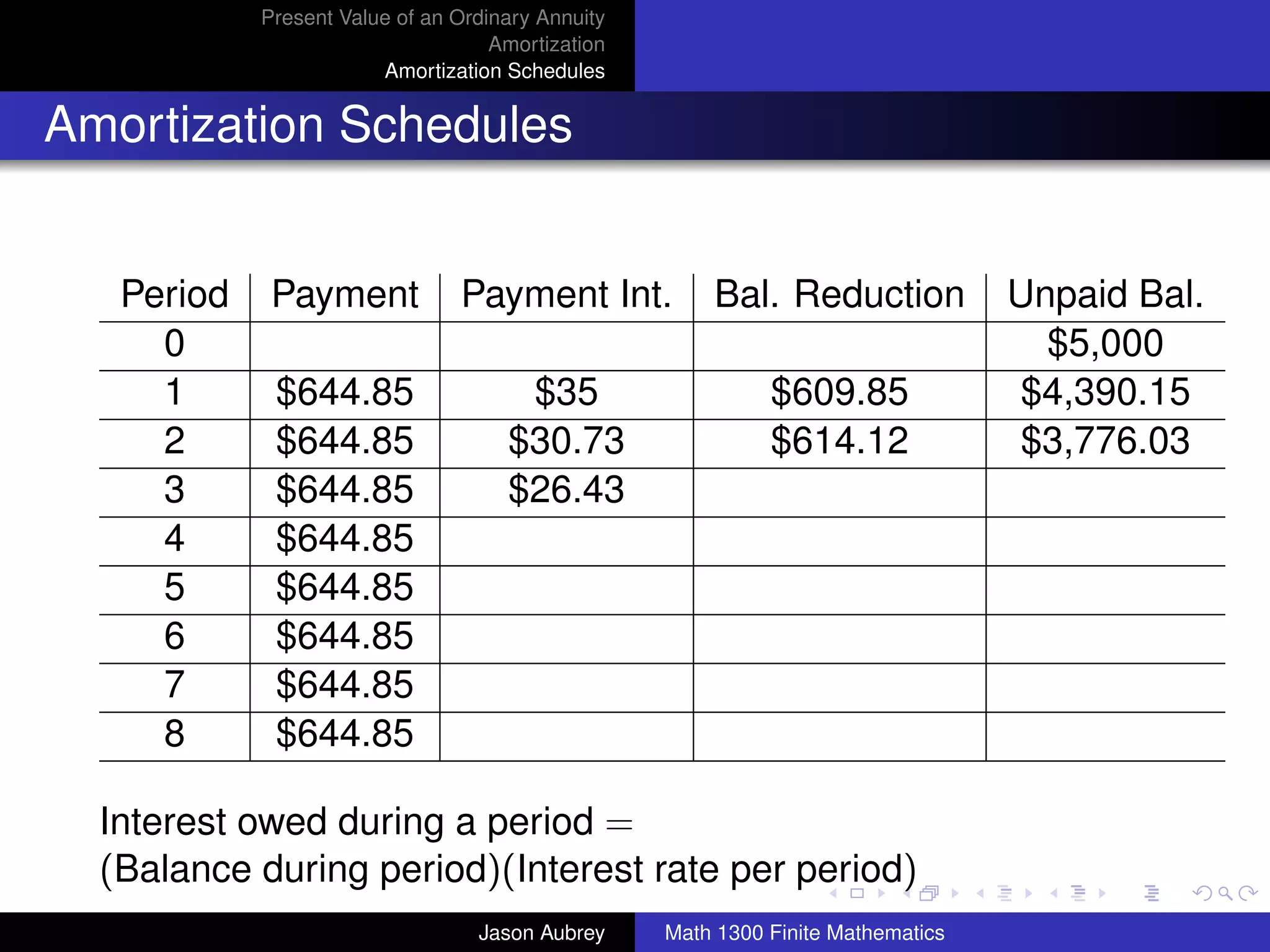
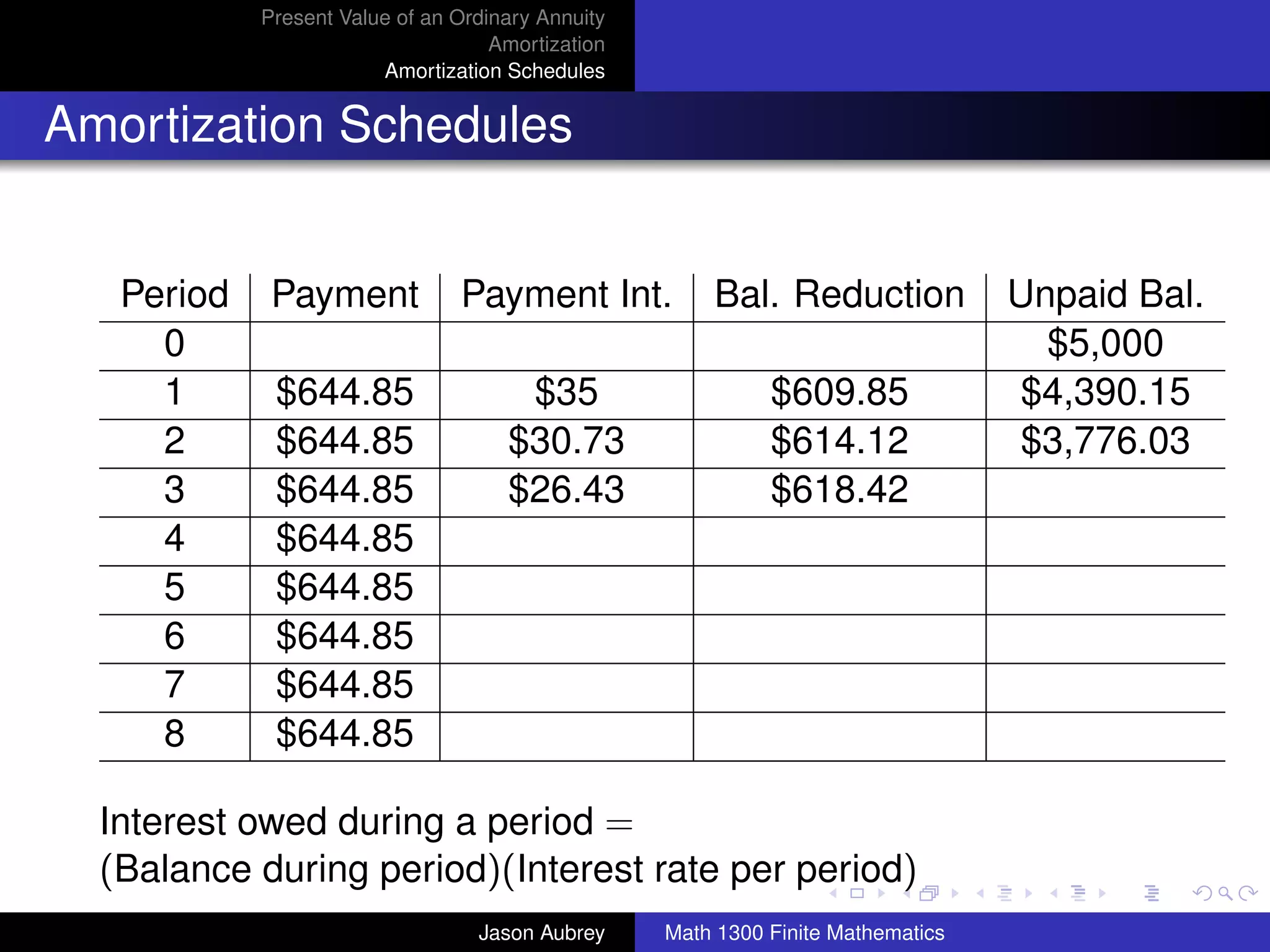
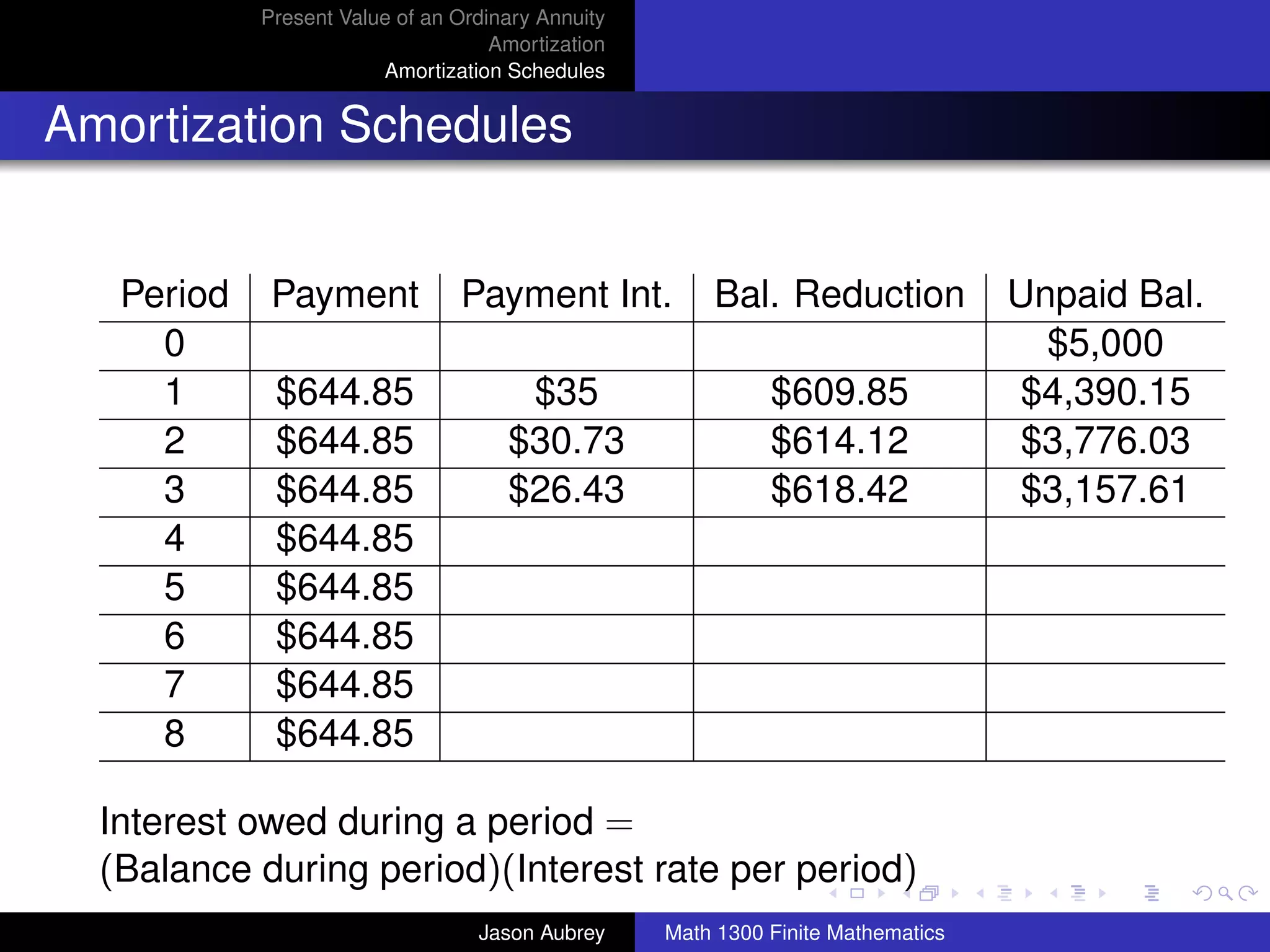
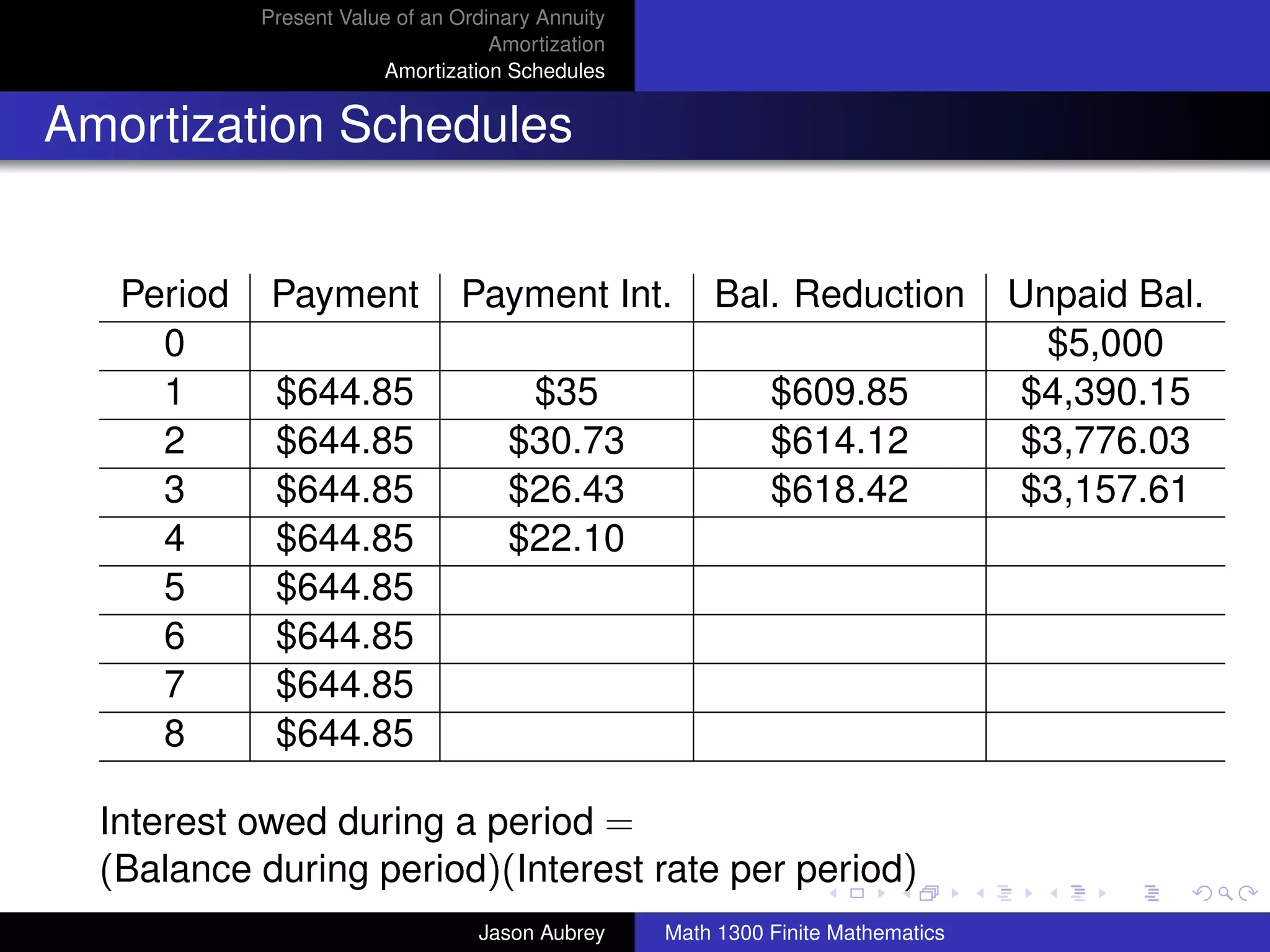
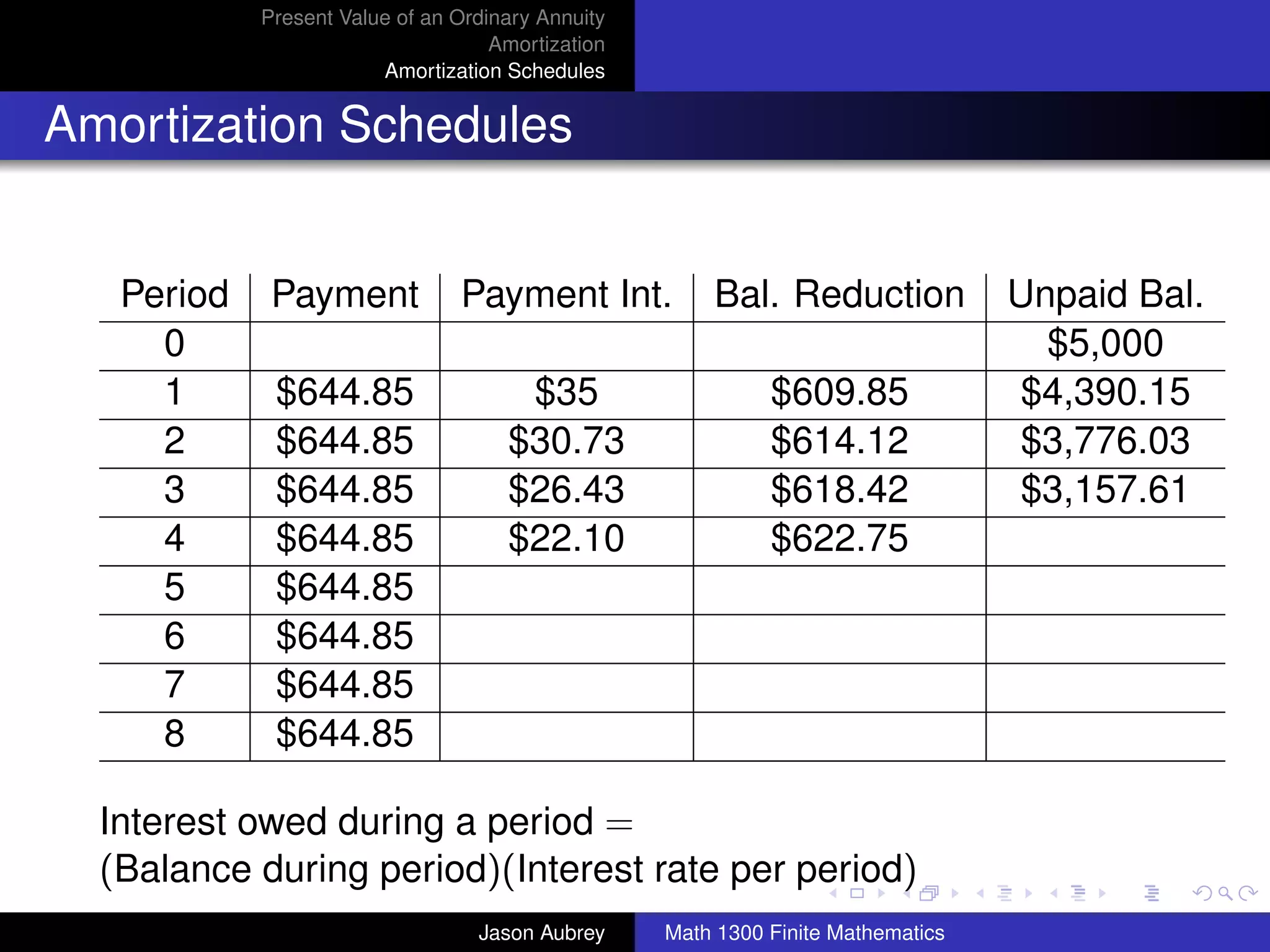
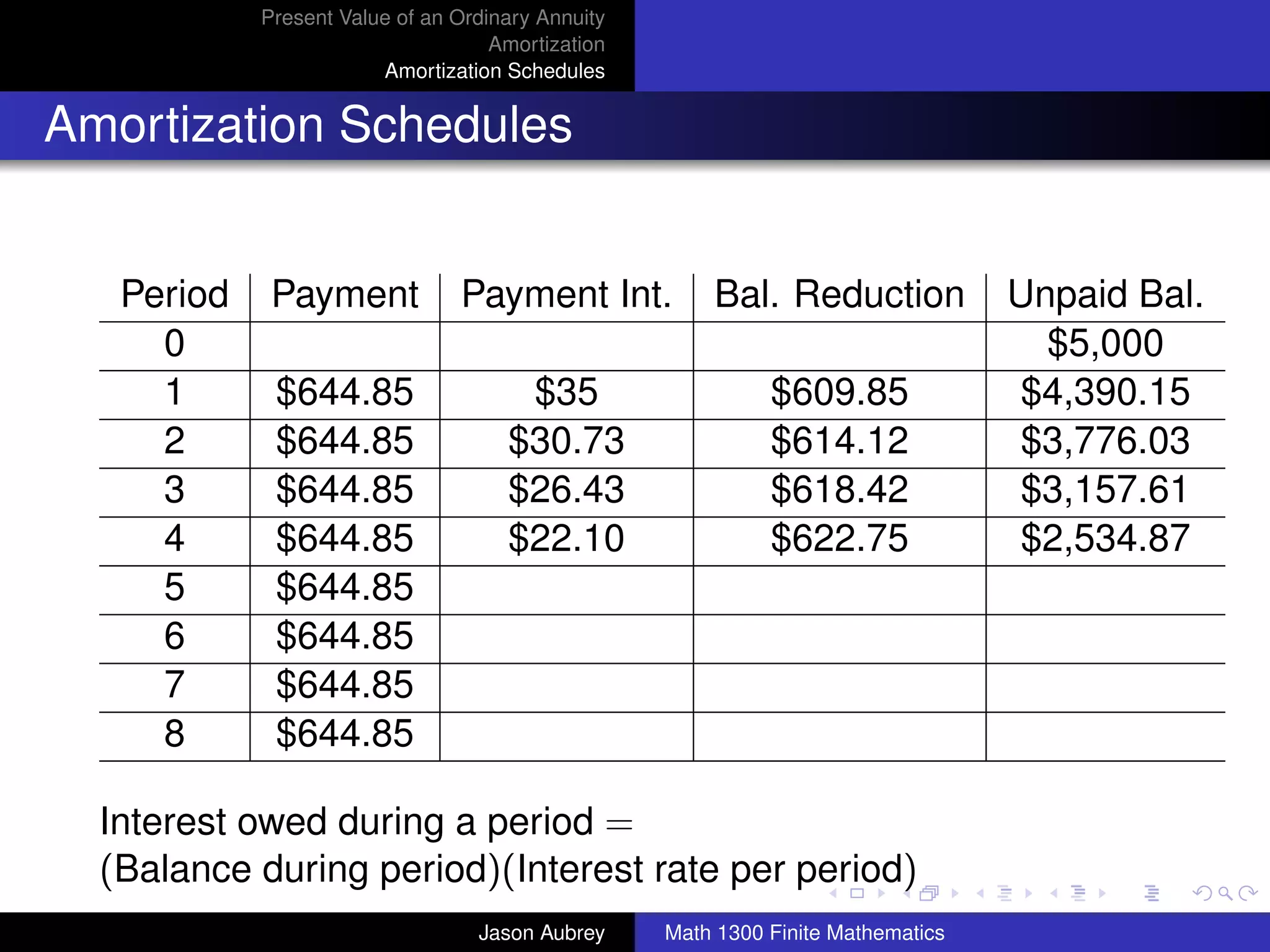
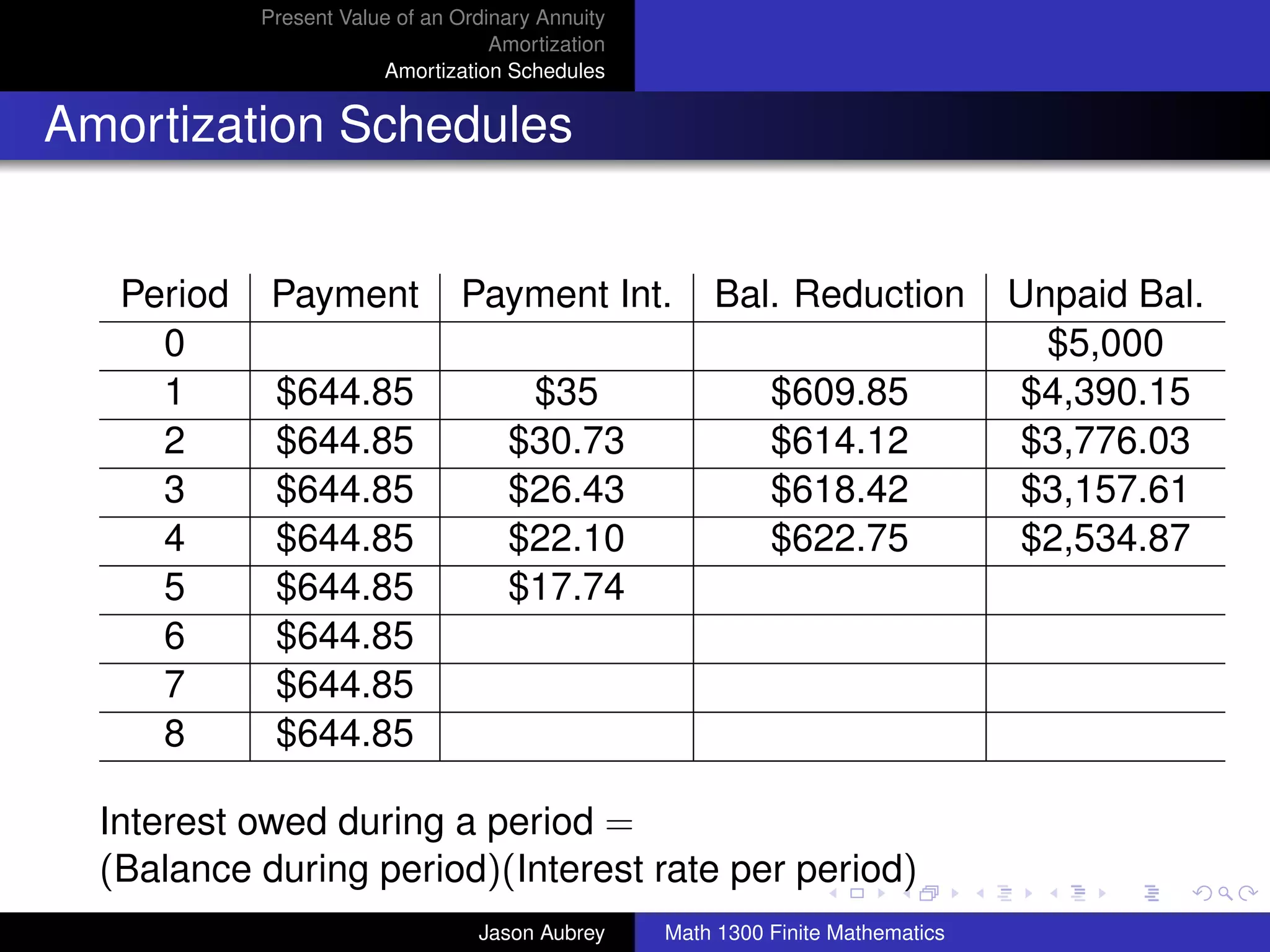
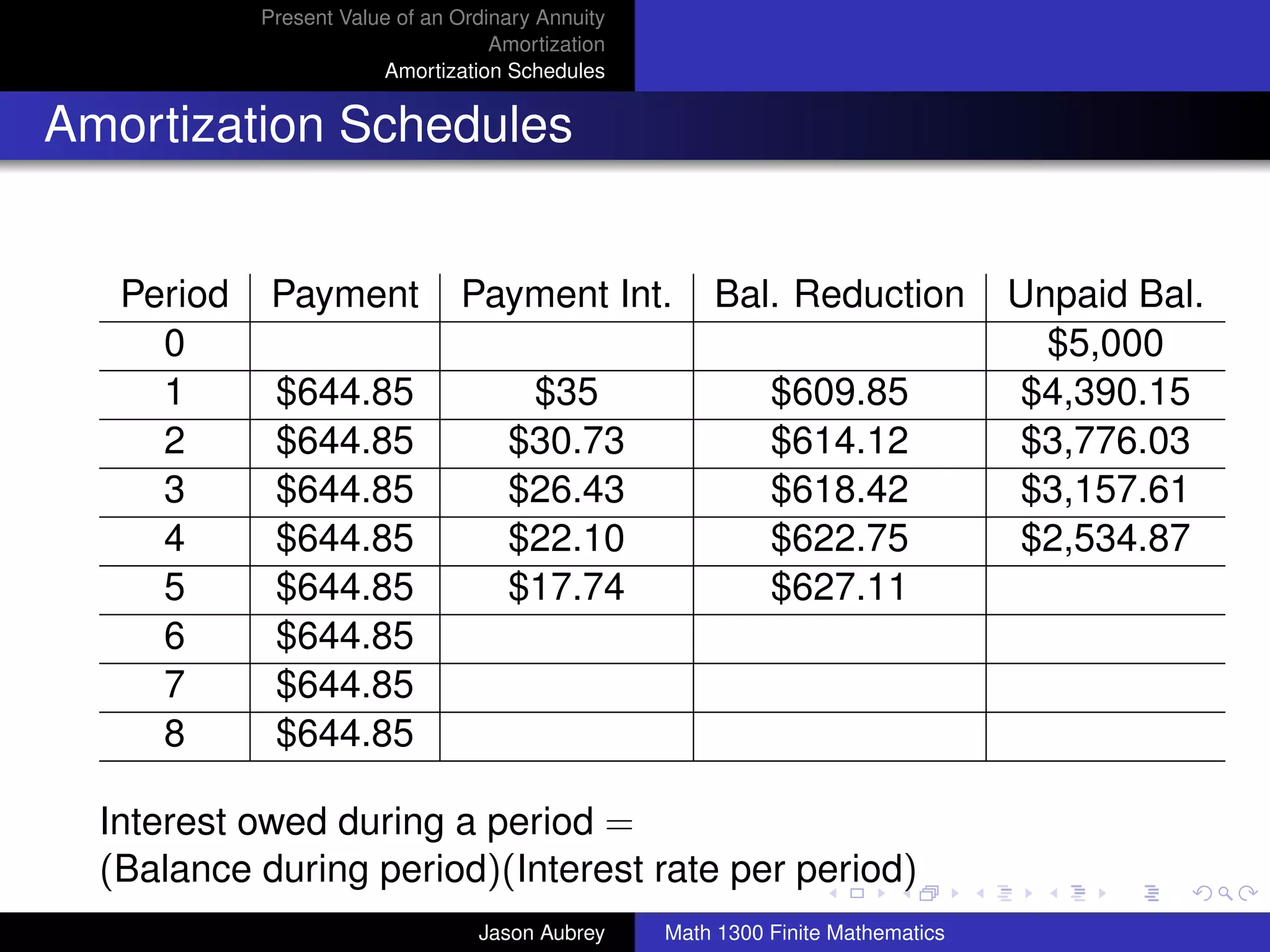
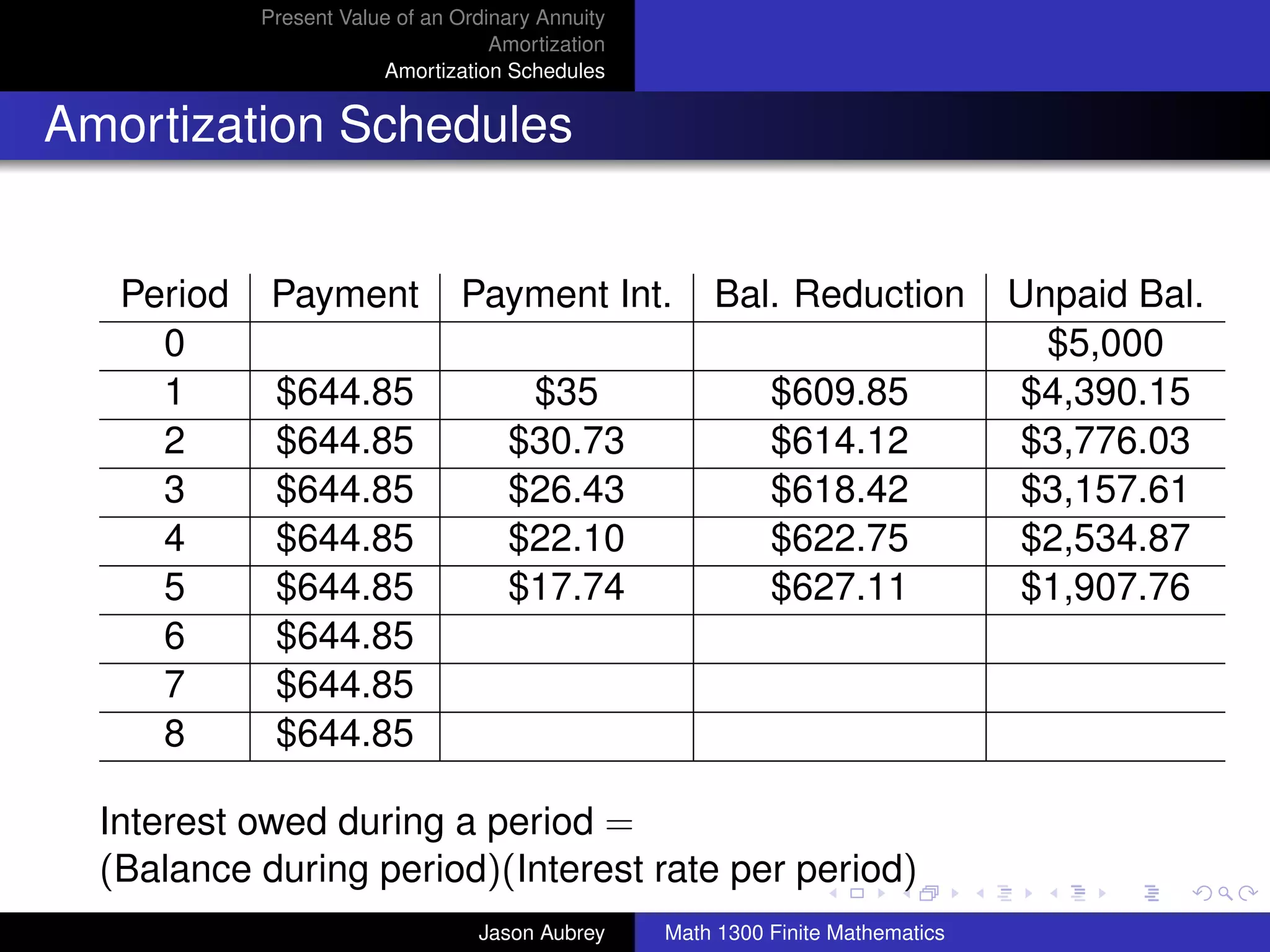
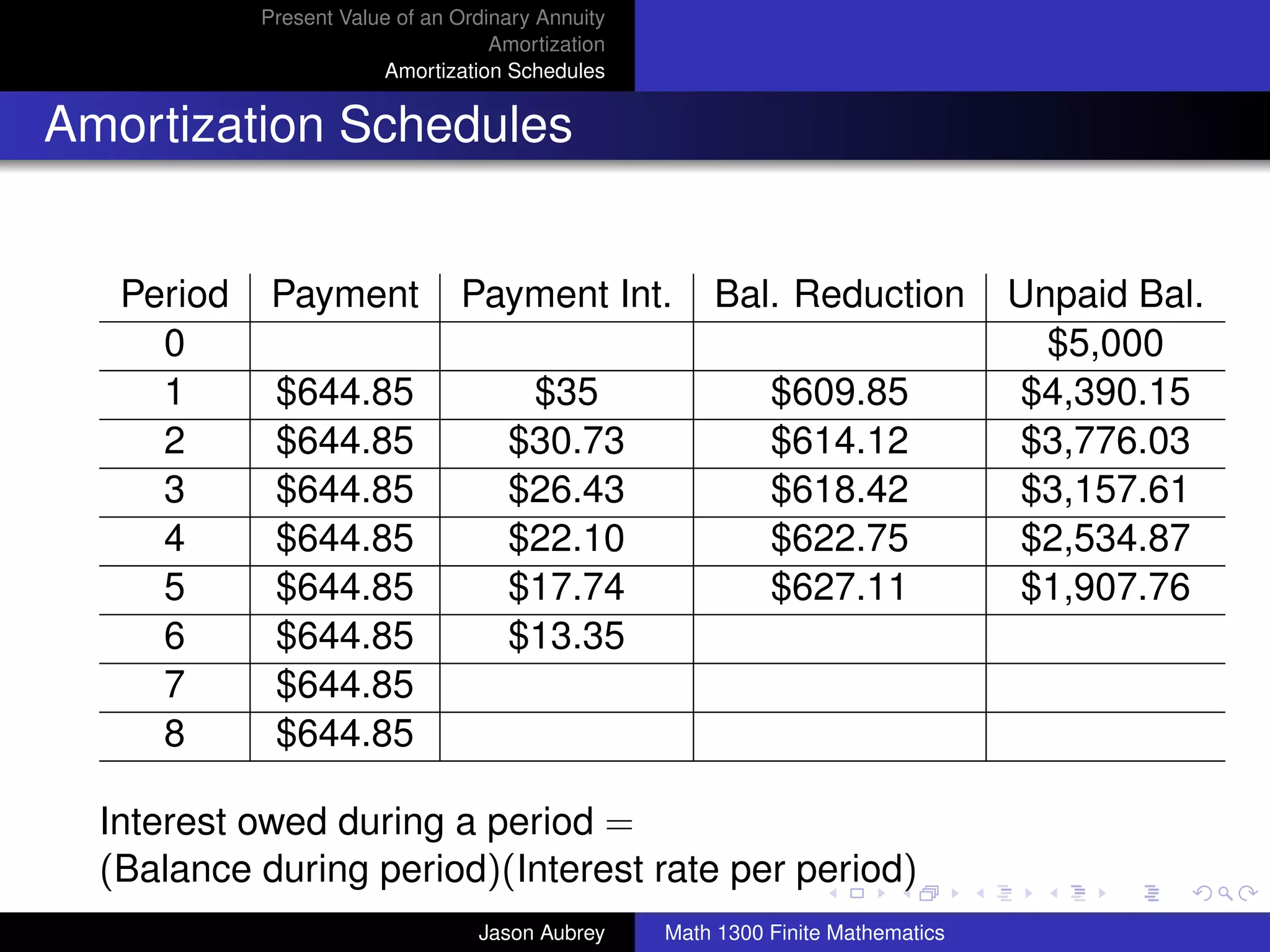
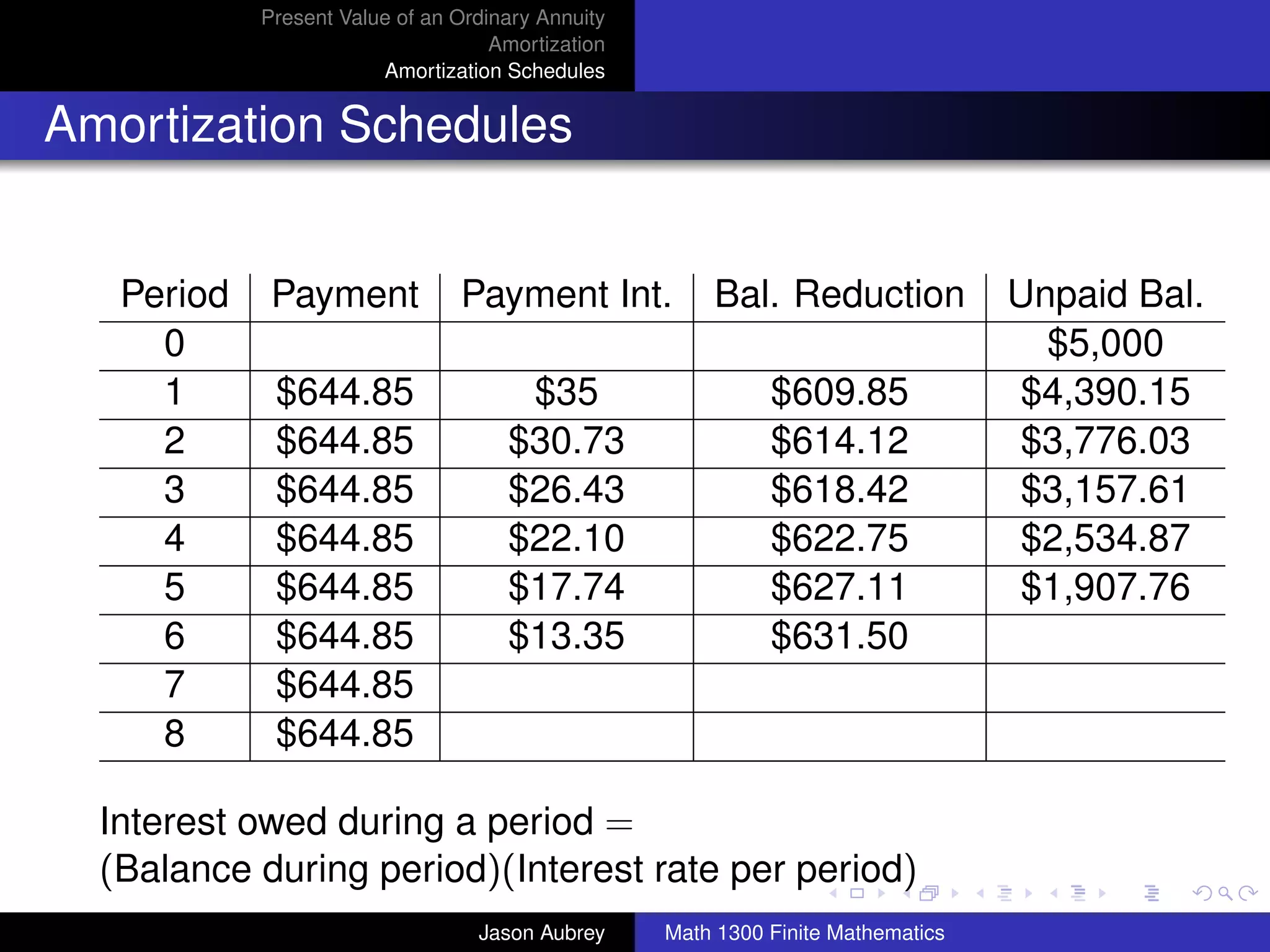
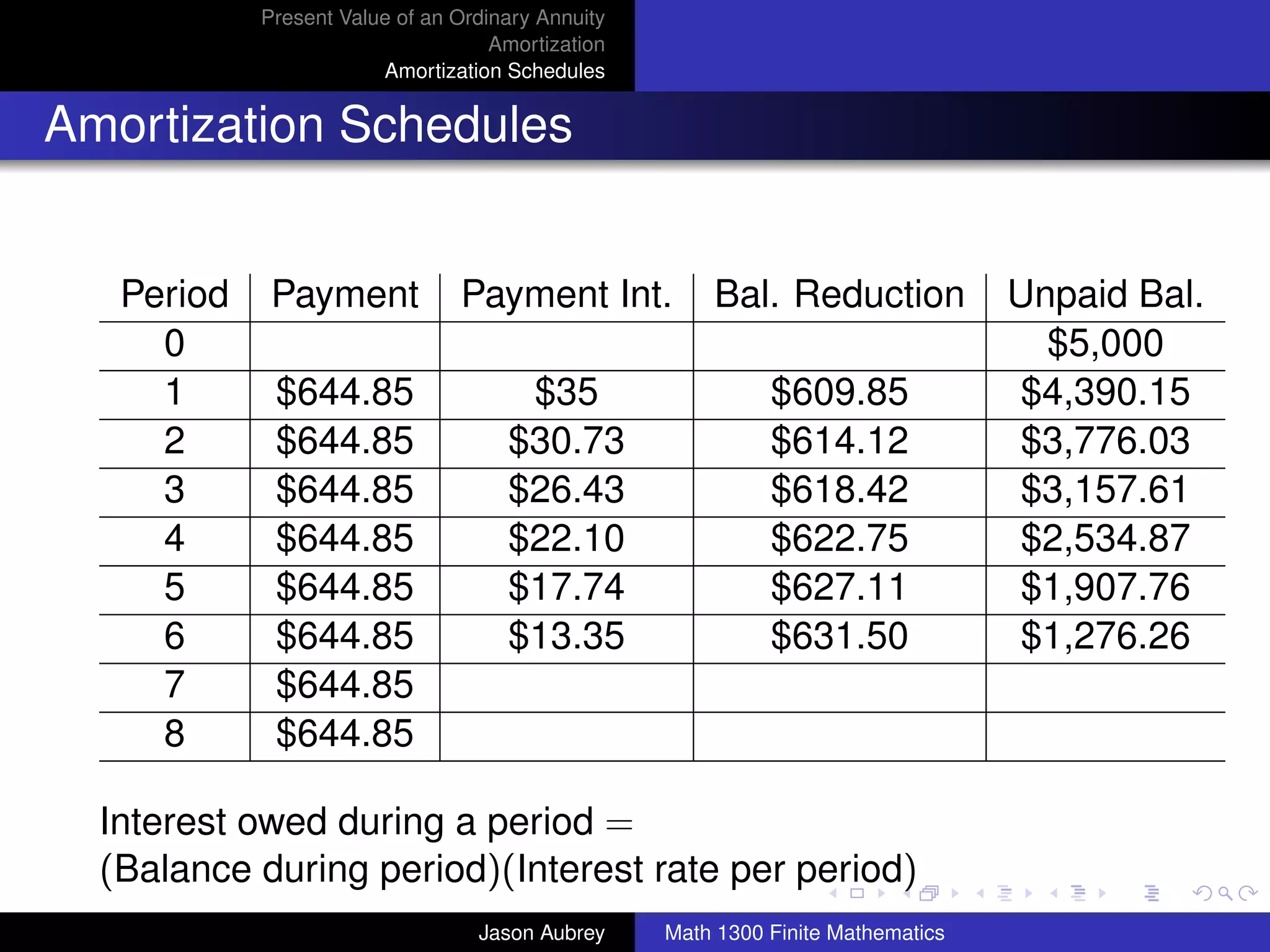
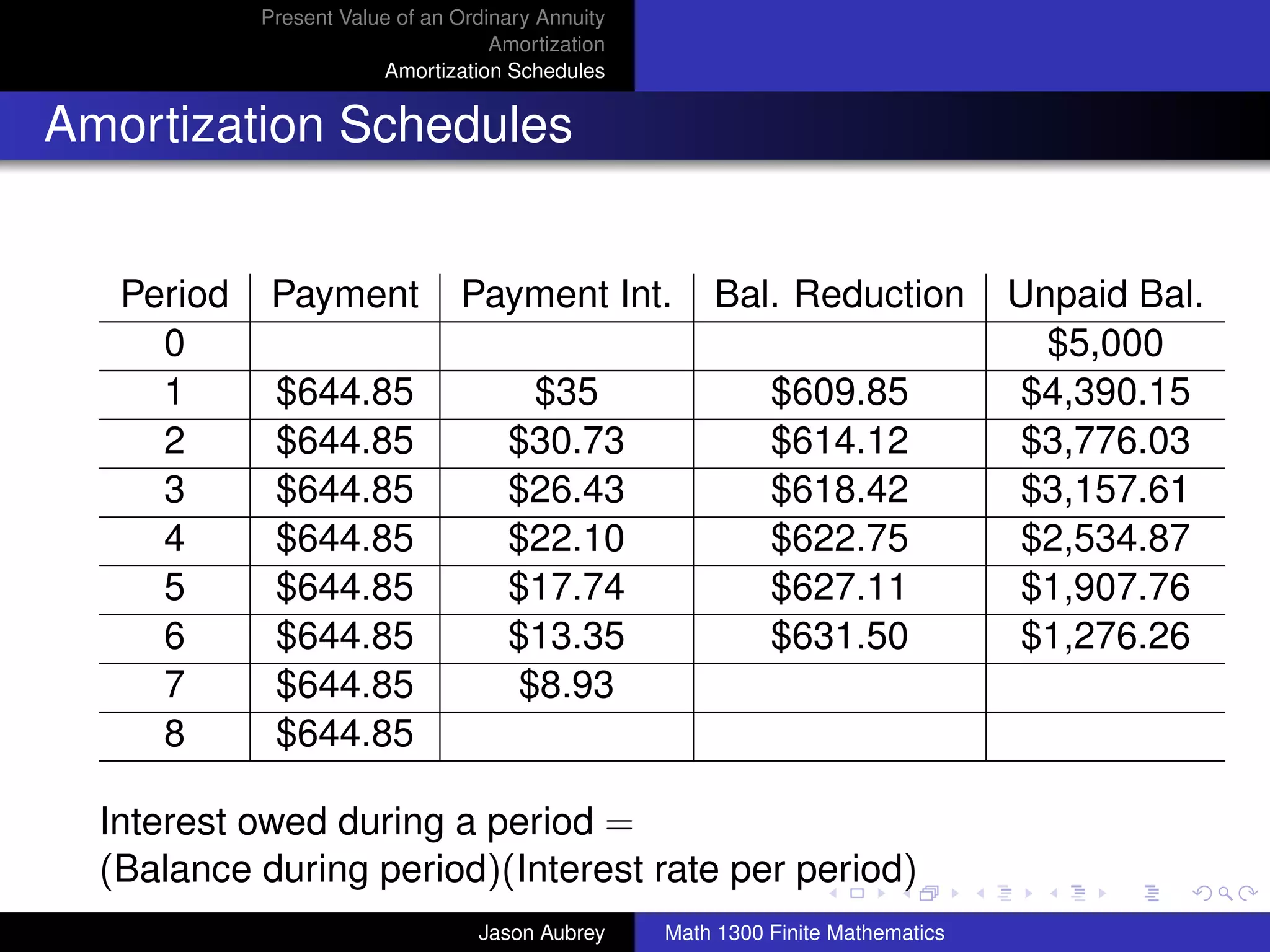
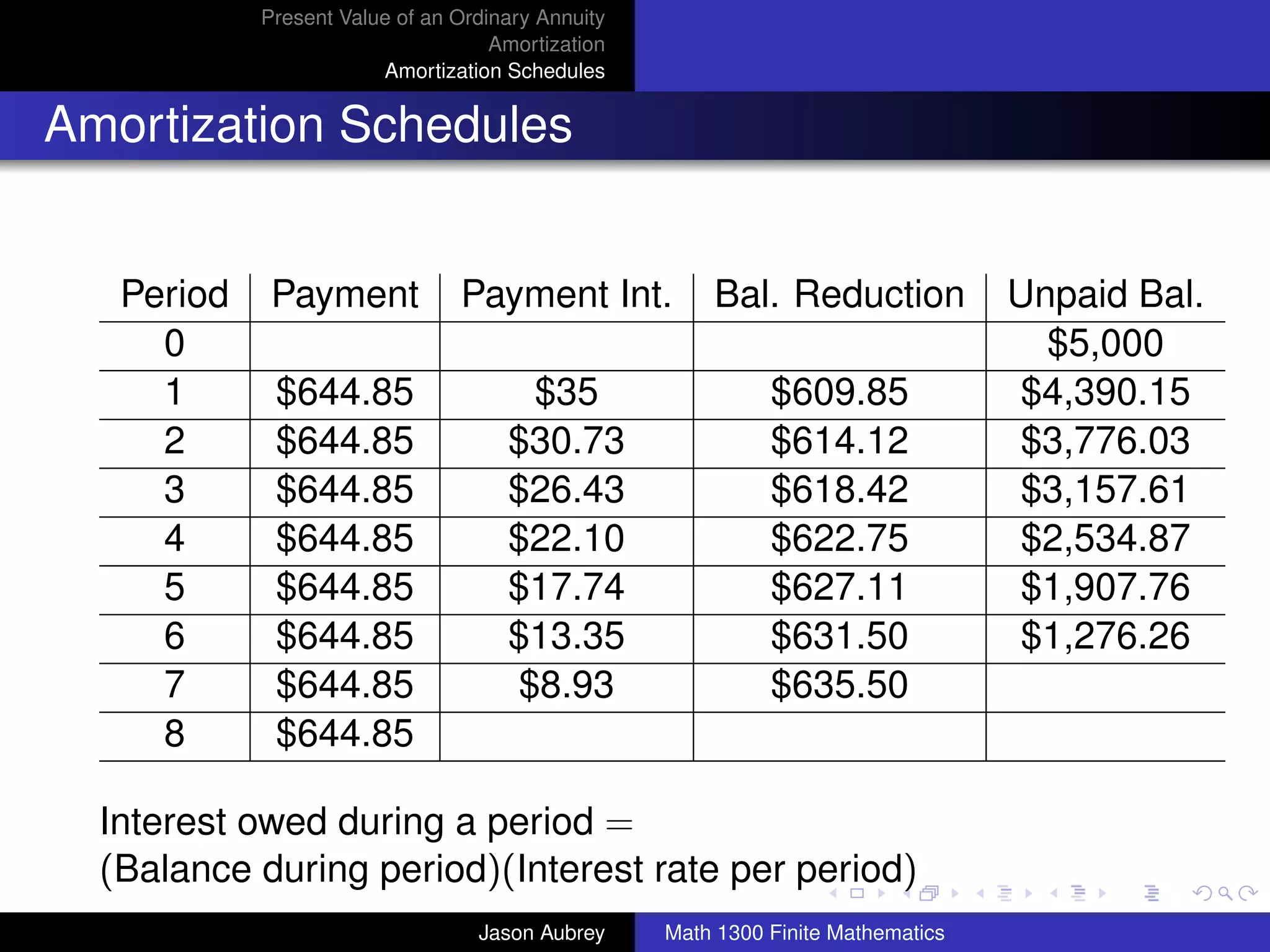
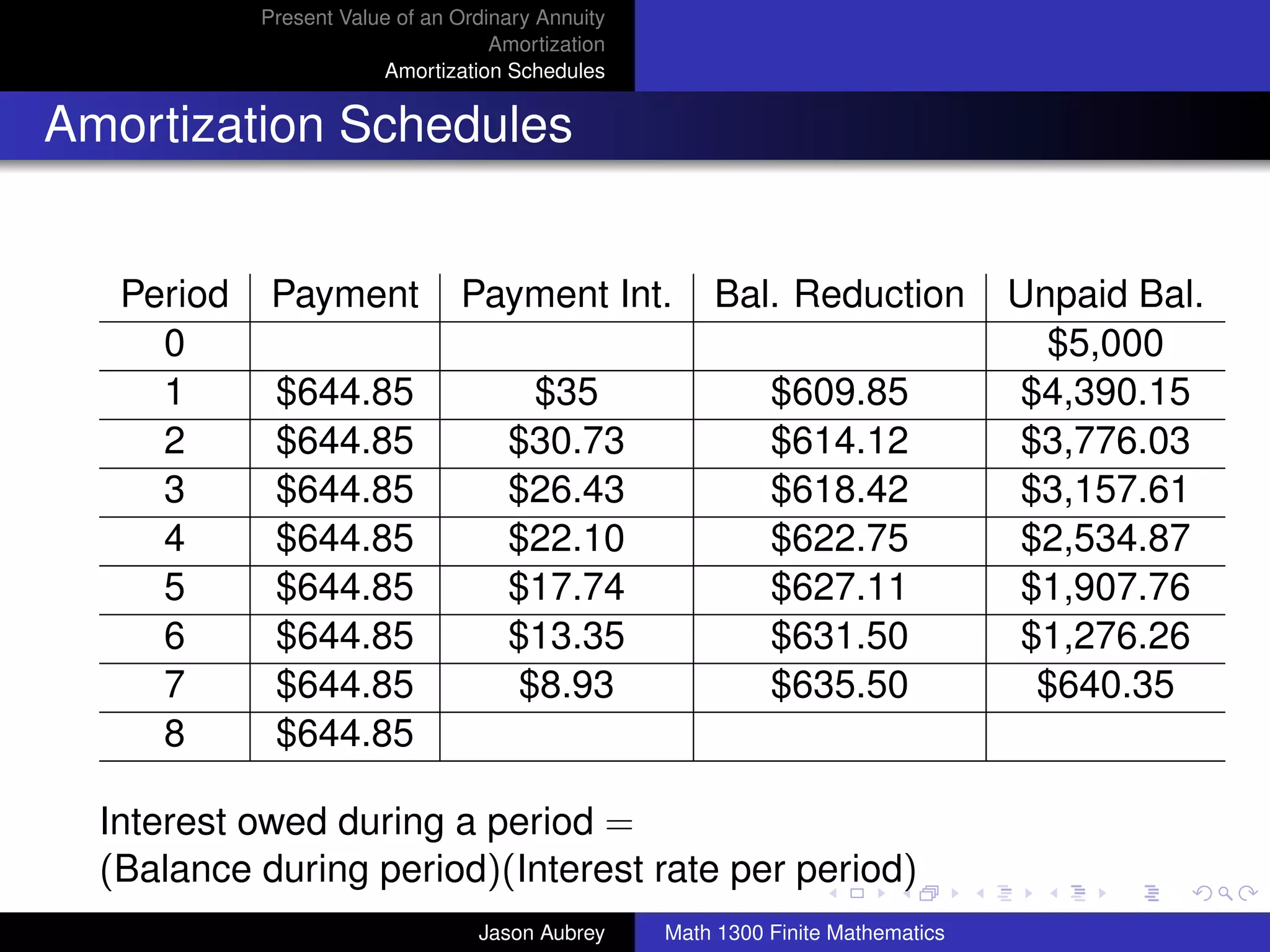
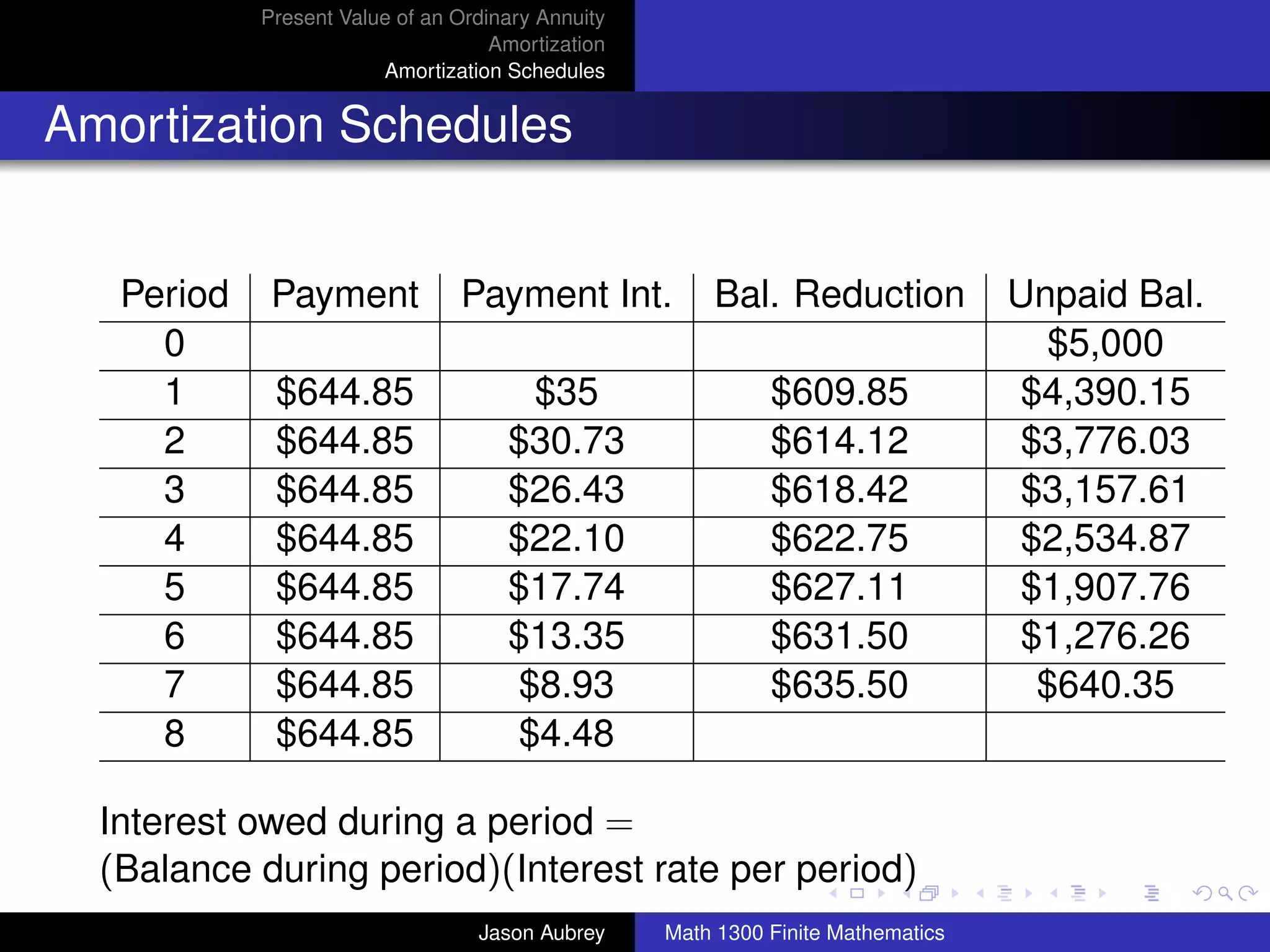
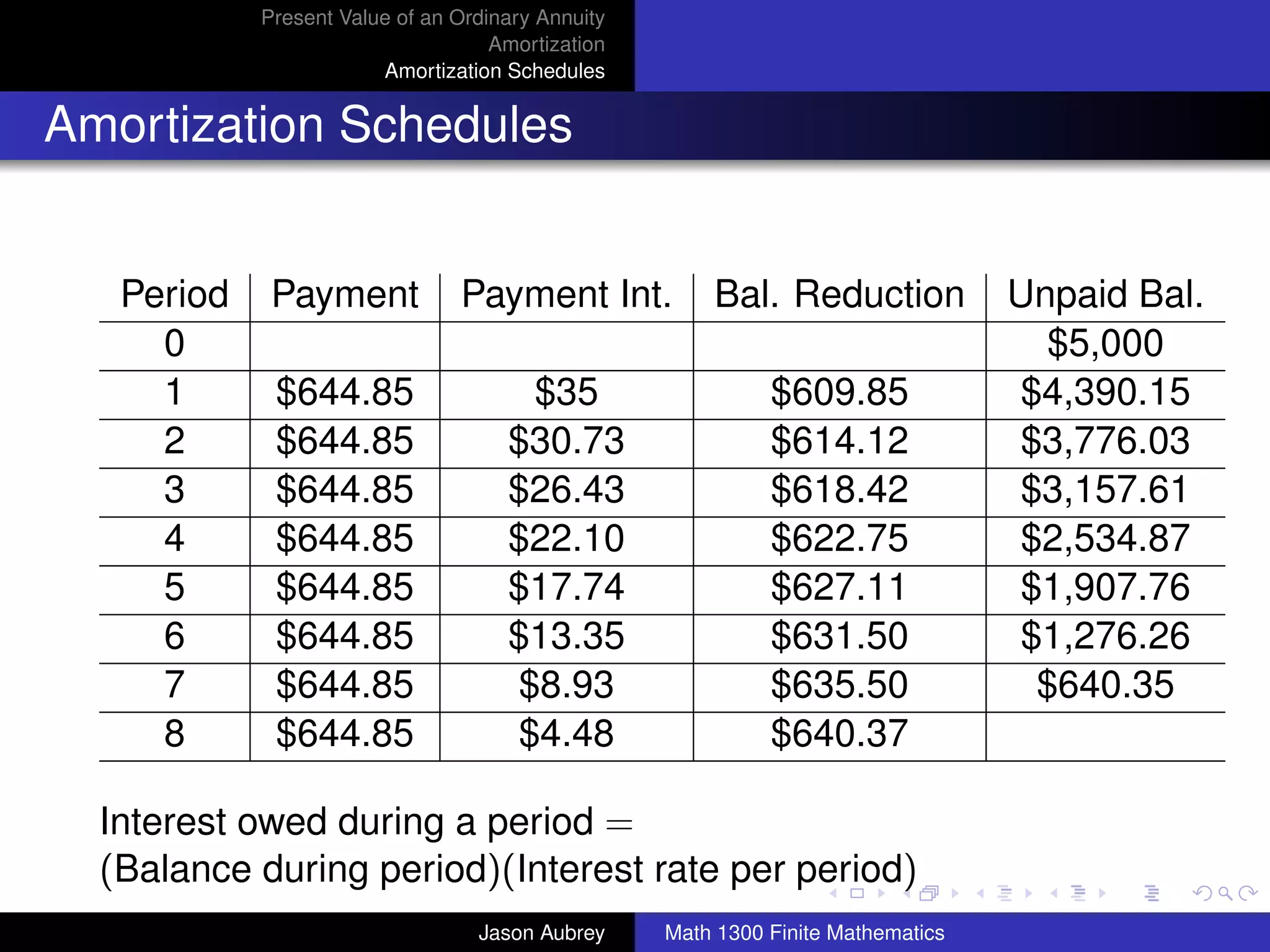
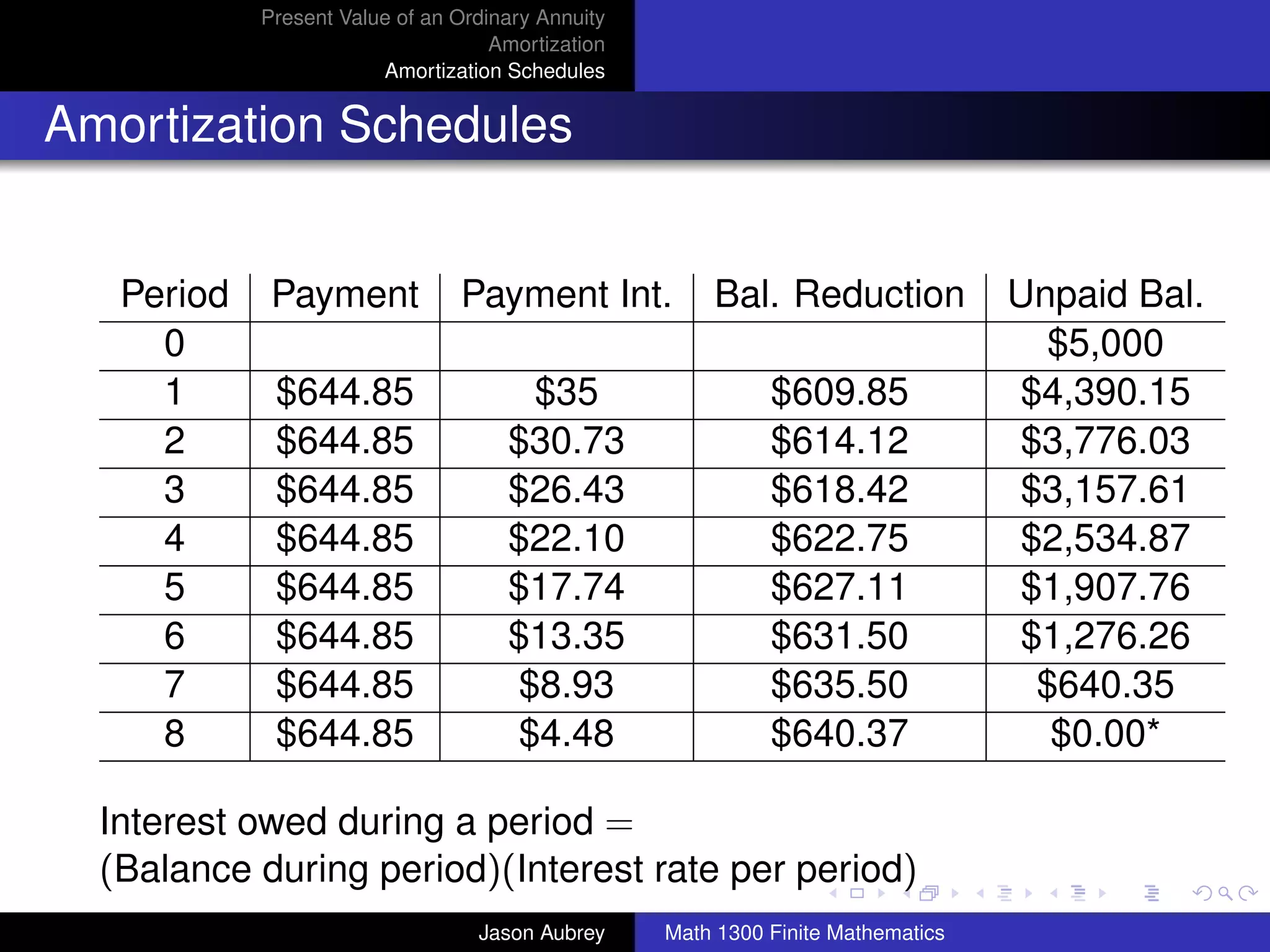
![Present Value of an Ordinary Annuity
Amortization
Amortization Schedules
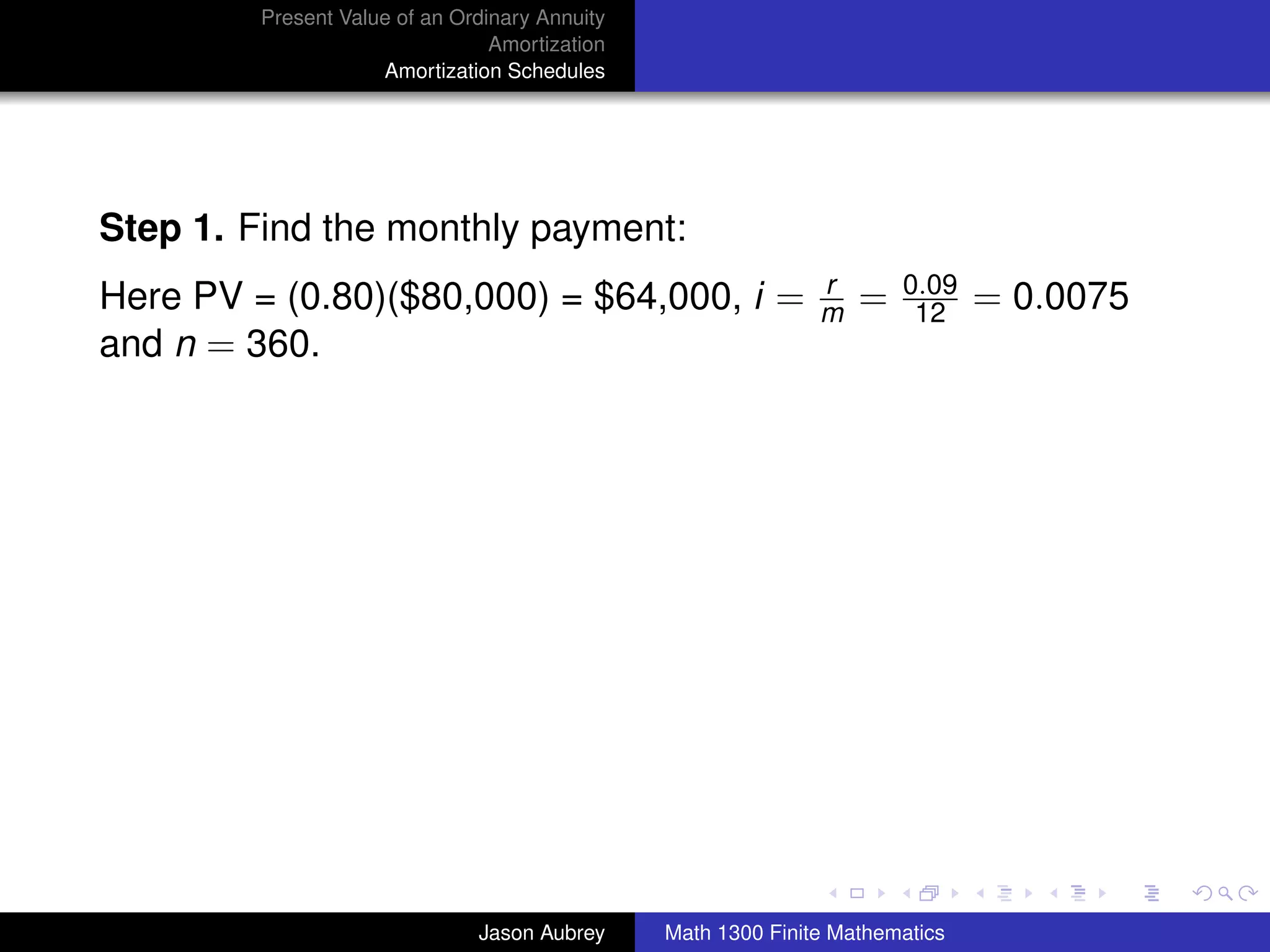
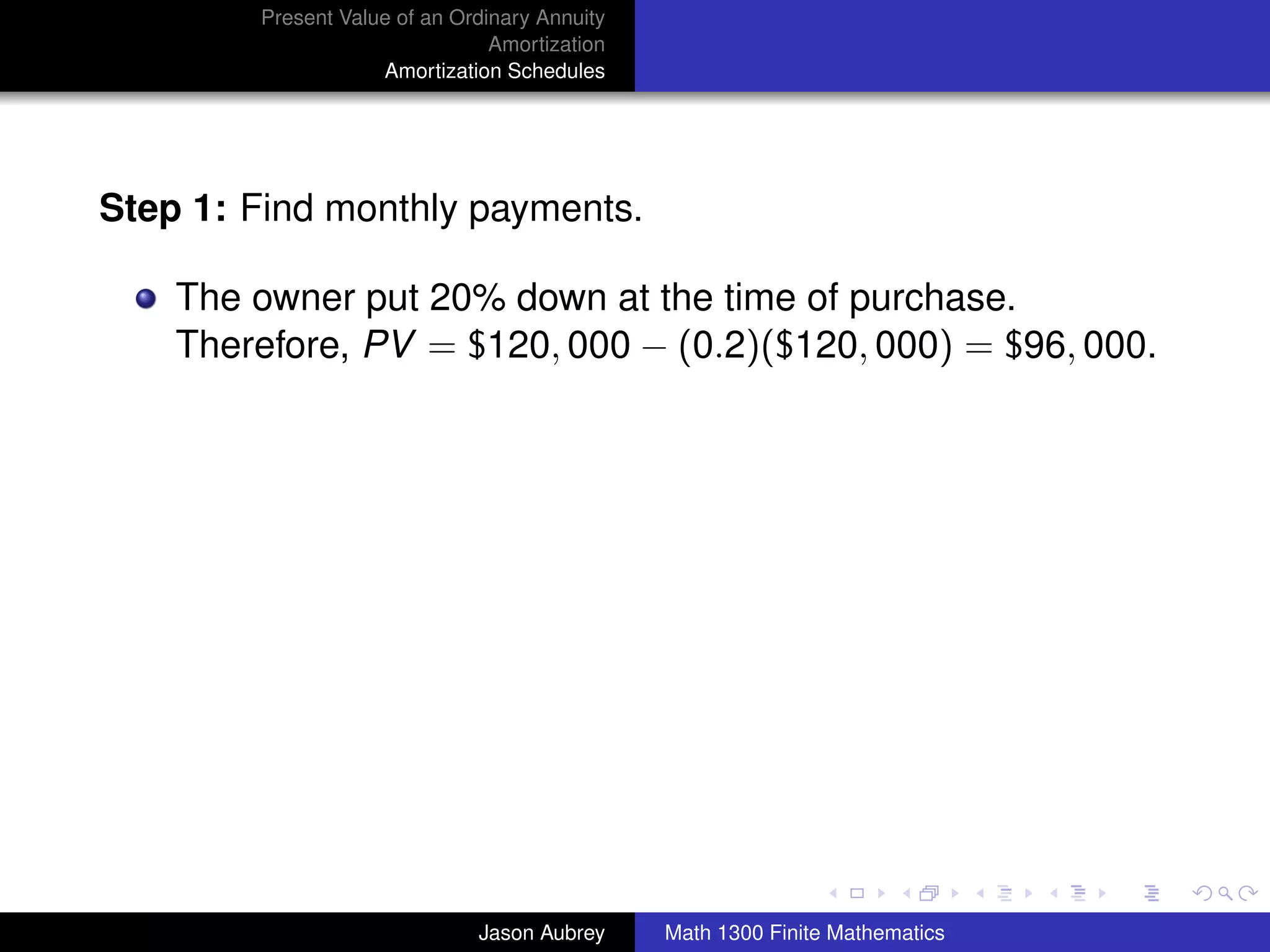
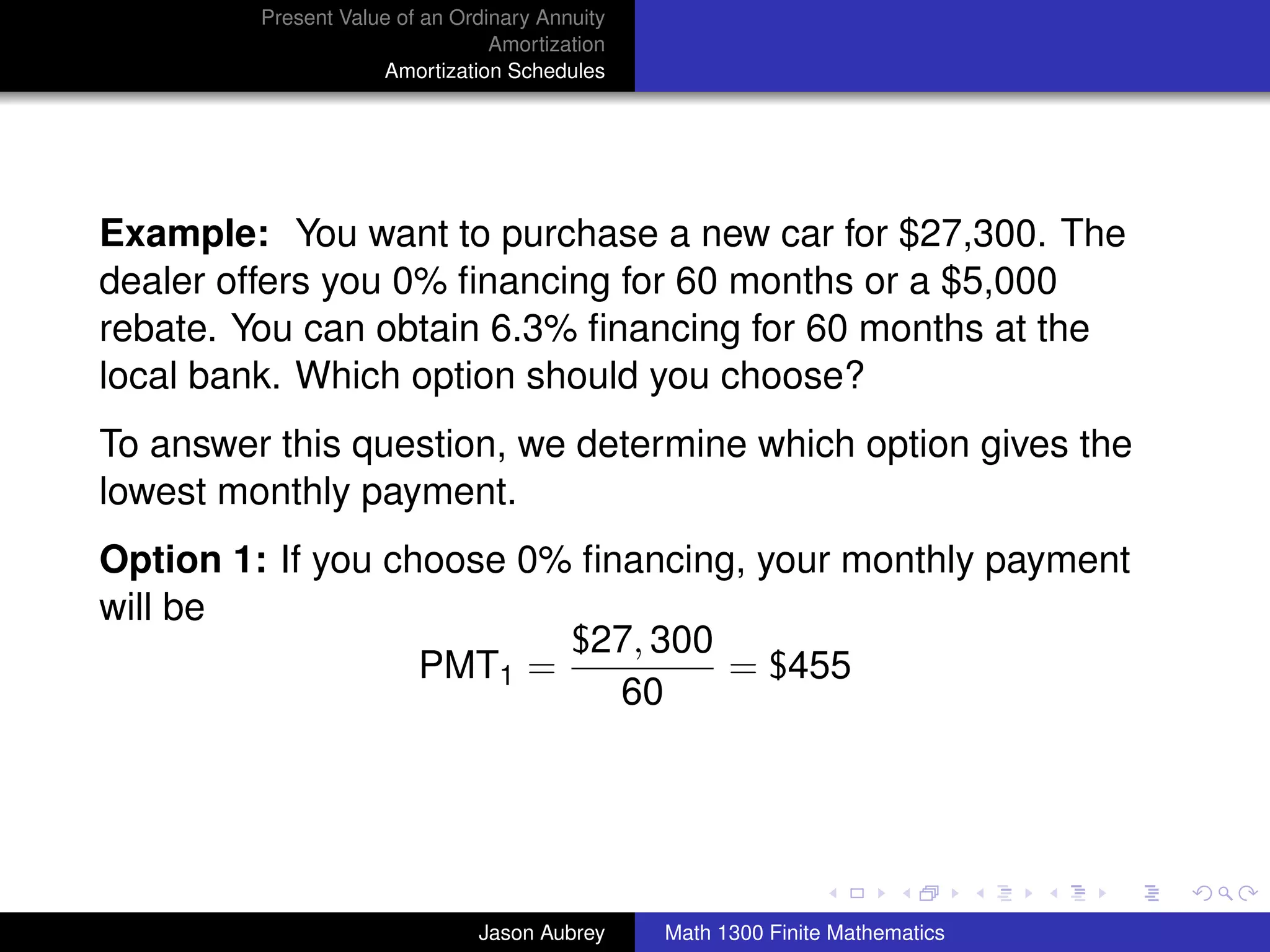
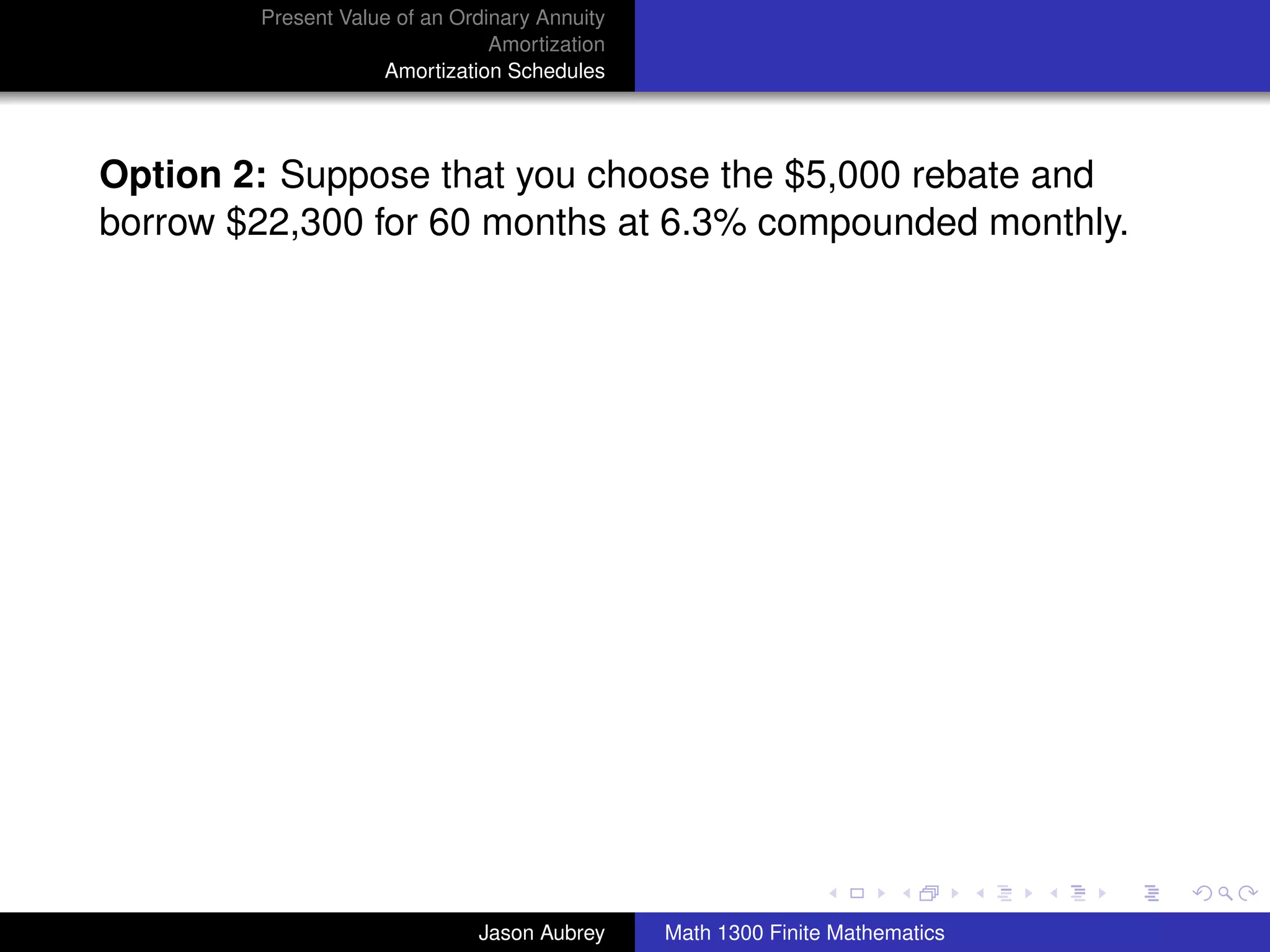
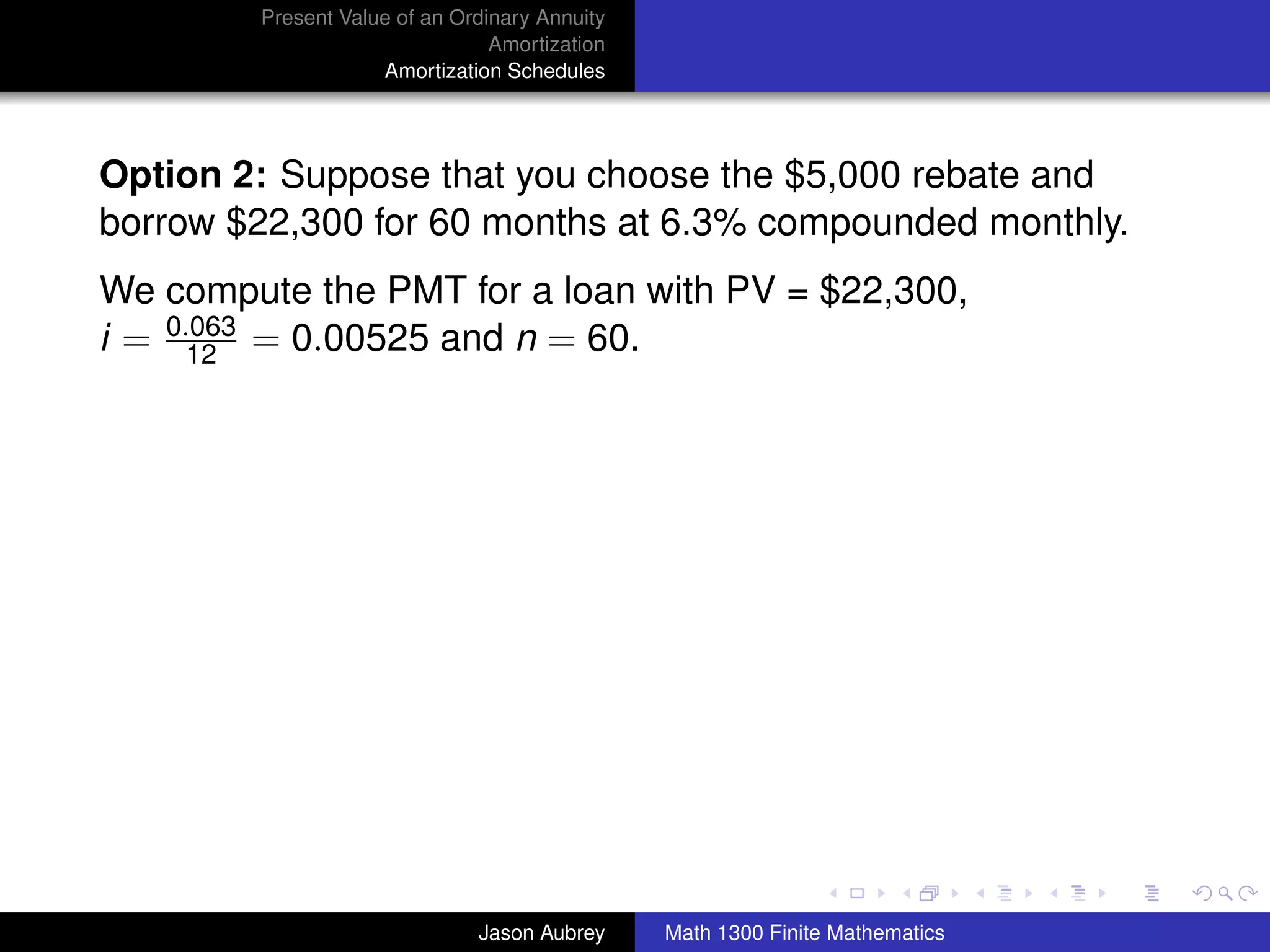
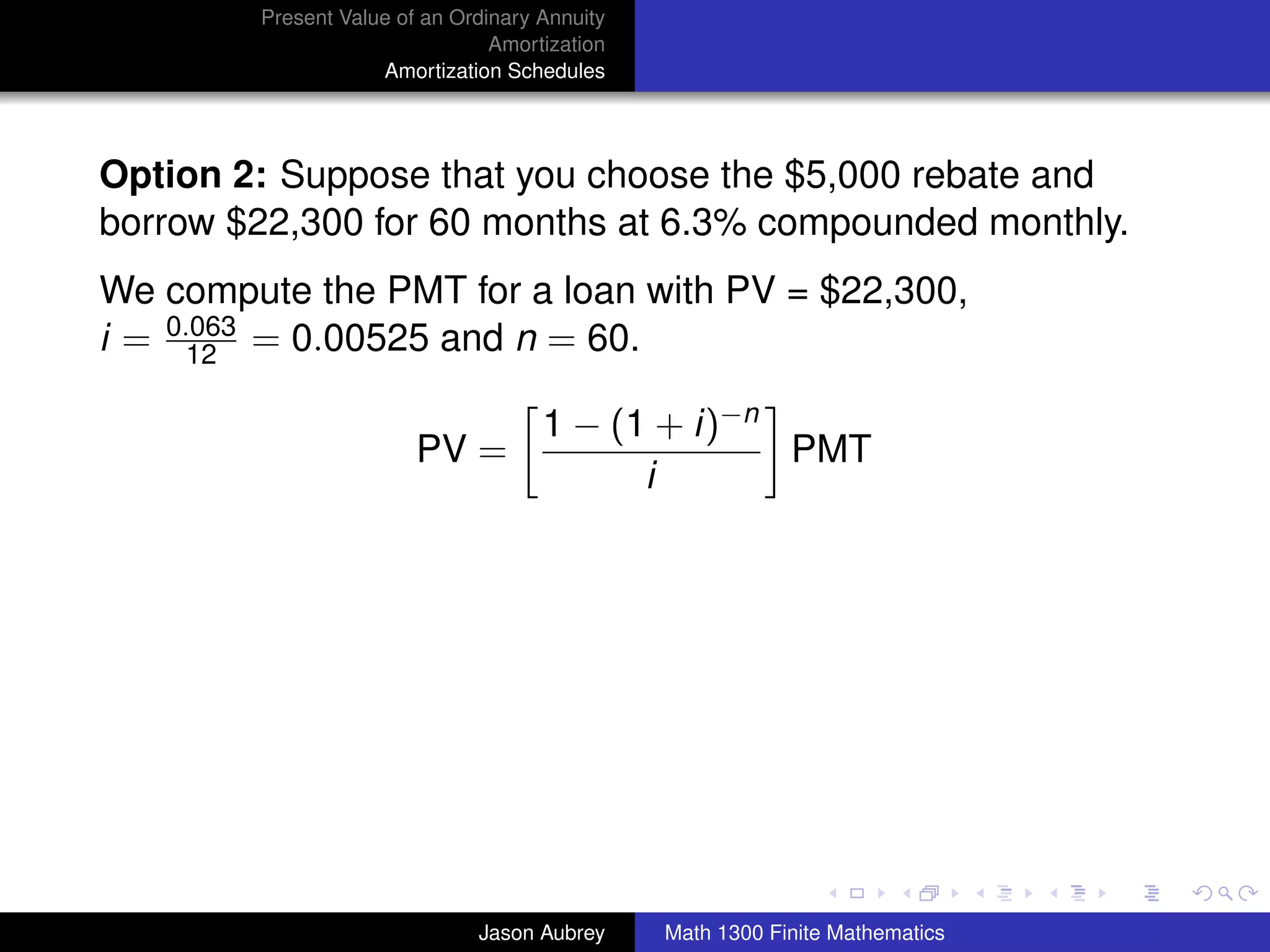
Example: A family purchased a home 10 years ago for
$80,000. The home was financed by paying 20% down and
signing a 30-year mortgage at 9% on the unpaid balance. The
net market value of the house (amount recieved after
subtracting all costs involved in selling the house) is now
$120,000, and the family wishes to sell the house. How much
equity (to the nearest dollar) does the family have in the house
now after making 120 monthly payments?
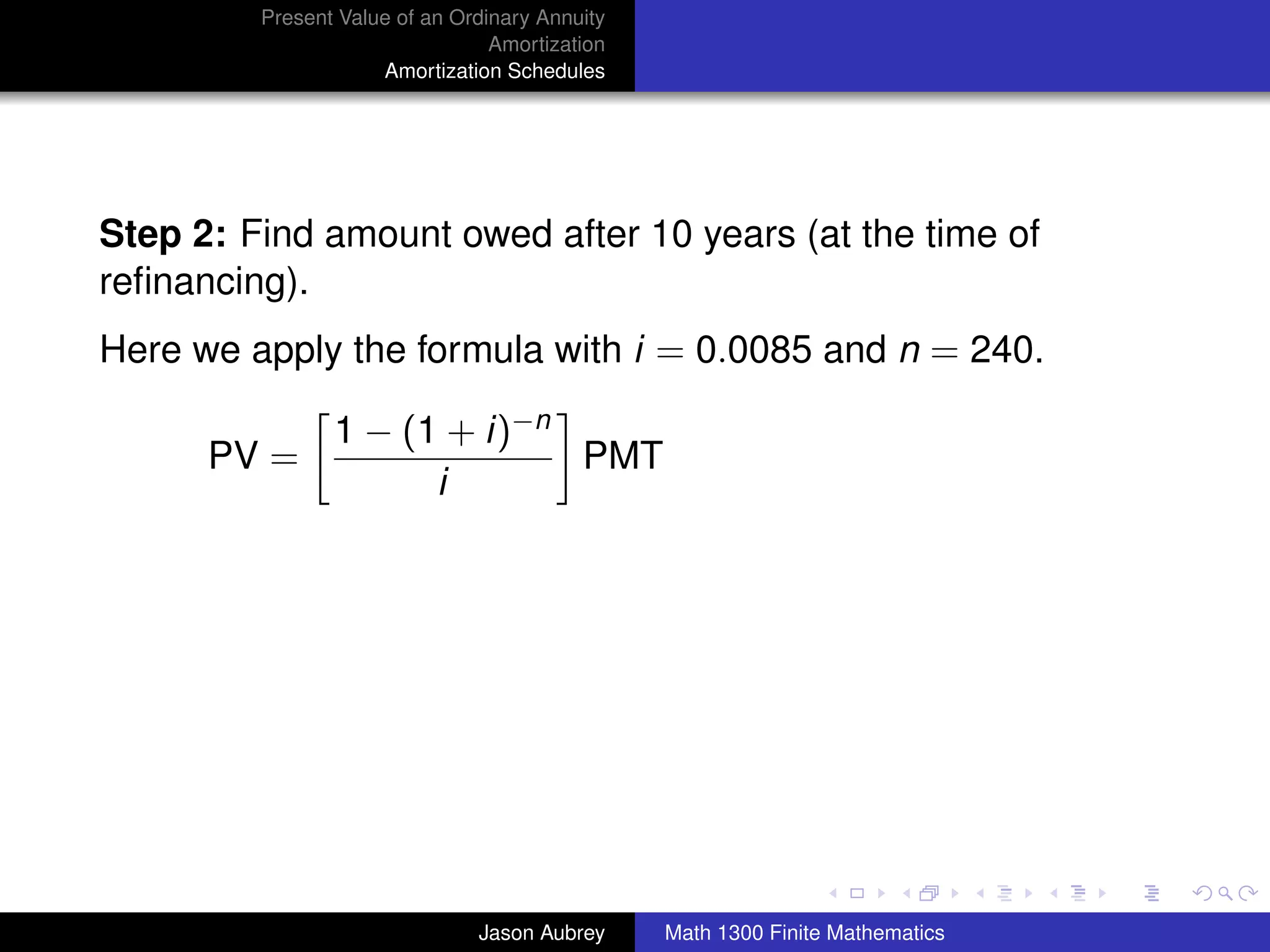
[Equity = (current net market value) - (unpaid loan balance)]
university-logo
Jason Aubrey Math 1300 Finite Mathematics](https://image.slidesharecdn.com/1300section34-090919152803-phpapp02/75/Math-1300-Section-3-4-Present-Value-of-an-Ordinary-Annuity-Amortization-77-2048.jpg)