This document discusses material balance applied to oil reservoirs. It introduces the Schilthuis material balance equation, which is a basic tool for interpreting and predicting reservoir performance. The general form of the material balance equation accounts for underground withdrawal of oil and gas, expansion of oil and originally dissolved gas, expansion of any gas cap gas, and changes in hydrocarbon pore volume due to water and pore volume changes. The document provides the specific equations that make up the material balance and shows how it can be simplified for different reservoir drive mechanisms, including solution gas drive above and below the bubble point pressure. It also provides examples of calculating recovery factors and gas saturation from the material balance equation for a reservoir undergoing primary depletion by solution gas drive.

1. Chapter 3
Material Balance Applied to Oil Reservoirs
§ 3.1 Introduction
-The Schilthuis material balance equation
- Basic tools of reservoir engineering
=> Interpreting and predicting reservoir performance.
-Material balance
1. zero dimension – this chapter
2. multi-dimension (multi-phase) – reservoir simulation

2. § 3.2 General form of the material balance equation for a
hydrocarbon reservoir
Underground withdrawal (RB)
= Expansion of oil and original dissolved gas (RB)………(A)
+ Expansion of gascap gas (RB) ……………… ………(B)
+ Reduction in HCPV due to connate water expansion and decrease in
the pore volume (RB)……………………… …….……(C)

3.  1
N = initial oil in place ( STB ) = Vφ (1 − S wc ) ( STB )
Boi
initial H .C. Vol. of the gascap SCF ft 3 bbl
m= (= const.) [=] or or
initial H .C. Vol. of the oil SCF ft 3 bbl
N p = cumulative oil production (STB )
cum. gas production ( SCF )
R p = cumulative gas − oil rato =
cum. oil production ( STB )

4. Expansion of oil & originally dissolved gas
Liquid exp ansion (oil exp ansion) = liq. (at p ) − liq. (at pi )
RB
= NBo − NBoi = N ( Bo − Boi )[=]STB [=]RB  (3.1)
STB
Liberated gas exp ansion = − [ solution gas (at p) − solution gas (at pi )]
SCF RB
= NRsi B g − NRs B g = N ( Rsi − Rs ) B g [=]STB [=]RB  (3.2)
STB SCF

5. Expansion of the gascap gas
Expansion of the gascap gas =gascap gas (at p) –gascap (at pi)
SCF RB
The total volume of gascap gas = mNBoi [=] STB [=]RB
SCF SCF
1 1
or G = mNBoi [=]RB [=]SCF
B gi RB
SCF
1 RB
Amount of gas (at p ) = mNBoi B g [=]SCF [=]RB
B gi SCF
Bg
Expansion of the gascap gas = mNBoi − mNBoi [ =]RB
B gi
Bg
= mNBoi ( − 1) ( RB)  (3.3)
B gi

6. Change in the HCPV due to the connate water expansion &
pore volume reduction
d ( HCPV ) = − dVw + dV f V f = the total pore vol. = HCPV /(1 − S w )
= −(c wVw + c f V f )∆p Vw = the connate water vol. = V f ⋅ S wc
HCPV
= −(c wV f ⋅ S wc + c f V f ) ∆p = −V f (c w S wc + c f )∆p = − (c w S wc + c f ) ∆p
(1 − S w )
c w S wc + c f
= −(1 + m) NBoi ( ) ∆p
1 − S wc

7. Underground withdrawal
Pr oduction at surface N p ( STB ) − oil N p R p ( SCF ) − gas
Underground withdrawal N p Bo ( RB) − oil ( N p R p − N p Rs ) B g ( RB) − gas
⇒ Underground withdrawal = N p Bo + N p ( R p − Rs ) B g = N p [ Bo + ( R p − Rs ) B g ]

8. The general expression for the material balance as
Bg
N p [ Bo + ( R p − Rs ) B g ] = N ( Bo − Boi ) + N ( Rsi − Rs ) B g + mNBoi ( − 1)
B gi
c w S wc + c f
+ (1 + m) NBoi ( )∆p + (We − W p ) Bw
1 − S wc
 ( Bo − Boi ) + ( Rsi − Rs ) B g  Bg   c w S wc + c f  
⇒ N p [ Bo + ( R p − Rs ) B g ] = NBoi  + m − 1 + (1 + m)
 1− S  ∆ p

 Boi B 
  gi   wc   
+ (We − W p ) Bw  (3.7)
Note : Bo , Rs , B g = f ( p)
We = f ( p, t )
Simple form : Pr oduction = Expansion of reservoir fluids
dV = c ⋅ V ⋅ ∆p
Main difficulty : measuring p

9. F = N ( Eo + mE g + mE f ,w ) + We Bw  (3.12)
where
F = N p [ Bo + ( R p − R s ) B g ] + W p B w [=]RB
E o = ( Bo − Boi ) + ( Rsi − Rs ) B g [=] RB
STB
Bg
E g = Boi ( − 1) [=] RB
B gi STB
c w S wc + c f
E f , w = (1 + m) Boi ( )∆p RB
1 − S wc STB

10. F = N ( E o + mE g + mE f , w ) + We Bw  (3.12)
 No initial gascap, negligible water influx c f & cw → 0
Eq.(3.12) ⇒ F = NE o  (3.13)
 With water influx eq(3.12) becomes
F We
= N + (3.14)
Eo Eo
 Eq.(3.12) having a combination drive-all possible sources of energy.

11. § 3.4 Reservoir Drive Mechanisms
Reservoir drive mechanism
-reducing the M.B to a compact form to
quantify reservoir performance
- Solution gas drive -determining the main producing
- Gascap drive characteristics,
-Natural water
drive
In terms of for example, GOR; water cut
- Compaction drive -determining the pressure decline in the
reservoir
- estimating the primary recovery factor

12. § 3.5 Solution gas drive
(a) above the B.P. pressure (b) below the B.P. pressure

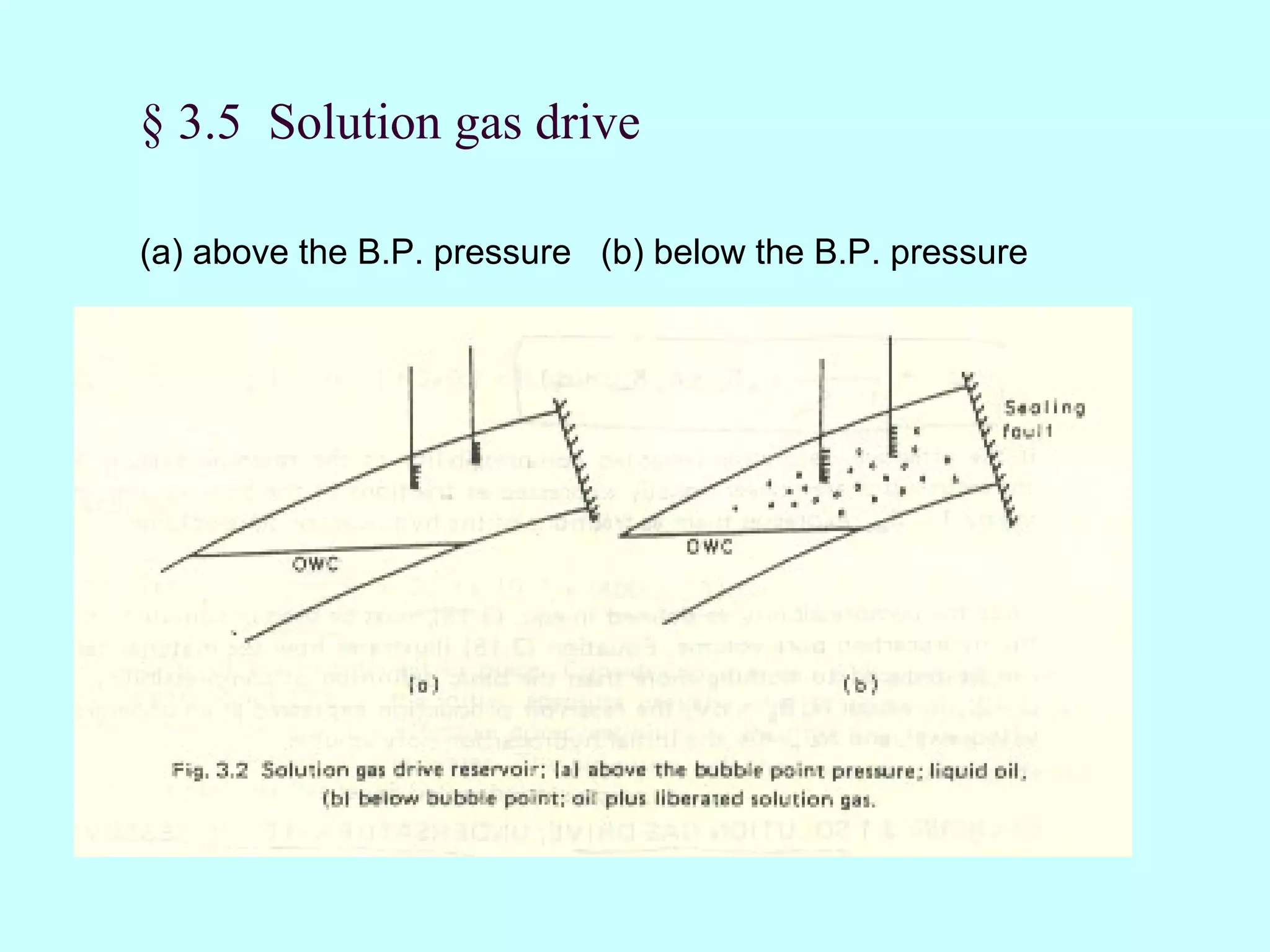
13. Above the B.P. pressure
- no initial gascap, m=0
- no water flux, We=0 ; no water production, Wp=0
- Rs=Rsi=Rp
from eq.(3.7)
 ( Bo − Boi ) + ( R si − R s ) B g  Bg   c w S wc + c f  
N p [ Bo + ( R p − R s ) B g ] = NBoi  + m − 1 + (1 + m)
 1− S
∆p 

 Boi B 
  gi   wc   
+ (We − W p ) B w  (3.7)
Note : ( R p − Rs ) = 0 ; ( Rsi − Rs ) = 0 ; m = 0 ;We = 0 ;W p = 0
( Bo − Boi ) (c w s wc + c f )
⇒ N p Bo = NBoi [ + ∆p ]
Boi 1 − S wc
cw S w + c f 1 dVo 1 dBo
⇒ N p Bo = NBoi [co + ( )]∆p co = − =−
1 − S wc Vo dp Bo dp
co S o + c w S w + c f − ( Boi − Bo ) ( Bo − Boi )
⇒ N p Bo = NBoi ( )∆p  (3.17) ≈ =
1 − S wc Boi ∆p Boi ∆p
or N p Bo = NBoi ce ∆p  (3.18) S o + S wc = 1
co S o + c w S w + c f
where ce = = the effective, saturation − weighted compressibility
1 − S wc

14. Exercise3.1 Solution gas drive, undersaturated oil reservoir
if p − pi → pb
Determine R.F. PVT − table 2.4 ( p.65)
c w = 3 × 10 −6 psi −1 c f = 8.6 × 10 −6 psi −1 S w = 0.2
Solution:
1 dVo 1 dBo
FromTable2.4(p.65) co = − =−
Vo dp Bo dp
Bob − Boi
pi = 4000 psi, Boi = 1.2417 RB co =
STB Boi ∆p
1.2511 − 1.2417
pb = 3330 psi, Bob = 12511 RB = = 11.3 ×10 −6 psi −1
STB 1.2417(4000 − 3330)
Eq(3.18)
N p Bo = NBoi c e ∆p
Np Boi
R.F . = = ce ∆p
N Pb
Bob
1.2417
= ×22.8 ×10 −6 ×( 4000 −3330)
1.2511
= 0.015 =1.5%

15. Table 2.4 Field PVT
P(psia) Bo (Rb/STB) Rs(SCF/STB) Bg( Rb/SCF)
4000 (pi) 1.2417 510
3500 1.2480 510
3300 (pb) 1.2511 510 0.00087
3000 1.2222 450 0.00096
2700 1.2022 401 0.00107
2400 1.1822 352 0.00119
2100 1.1633 304 0.00137
1800 1.1450 257 0.00161
1500 1.1287 214 0.00196
1200 1.1115 167 0.00249
900 1.0940 122 0.00339
600 1.0763 78 0.00519
300 1.0583 35 0.01066

16. Bo as Function of Pressure

17. Rs as Function of Pressure

18. Bg and E as Function of Pressure

19. Producing Gas-oil Ratio (R) as Function of Pressure

20. Note :
co S o + c w S w + c f
ce =
1 − S wc
1
= (11.3 × 10 −6 × 0.8 + 3 × 10 −6 × 0.2 + 8.6 × 10 −6 )
1 − 0.2
= 22.8 × 10 −6
4000 − 3330
∆p % = = 0.167 = 16.7%
4000

21. Below B.P. pressure (Saturation oil)
P<Pb =>gas liberated from saturated oil
1 1 1
cg ≈ = = 300 ×10−6 psi −1 = cg = 300 ×10−6 psi −1
p Pb 3300
co = 11.3 ×10−6 psi −1
cw = 3 ×10−6 psi −1
c f = 8.6 ×10−6 psi −1

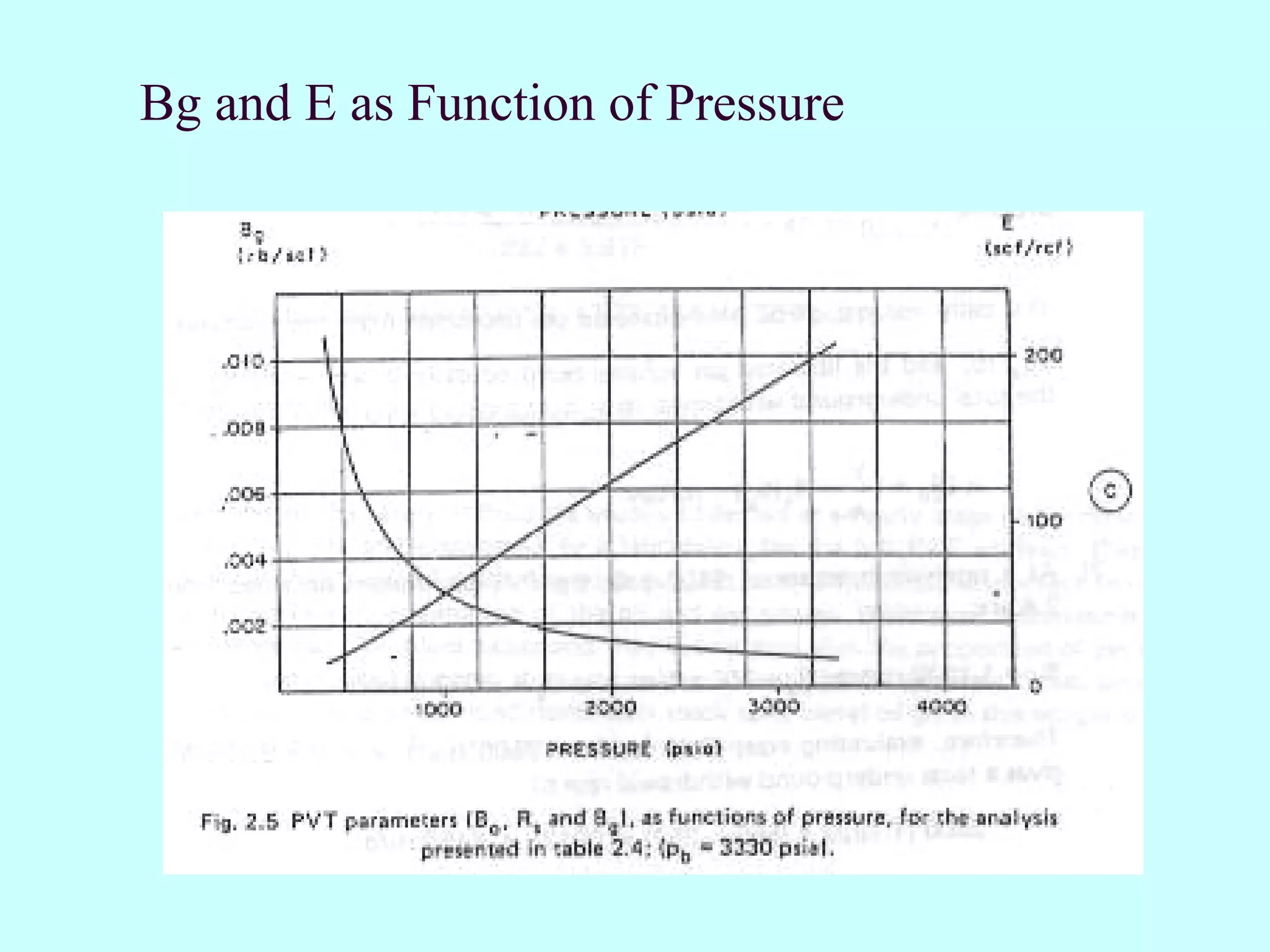
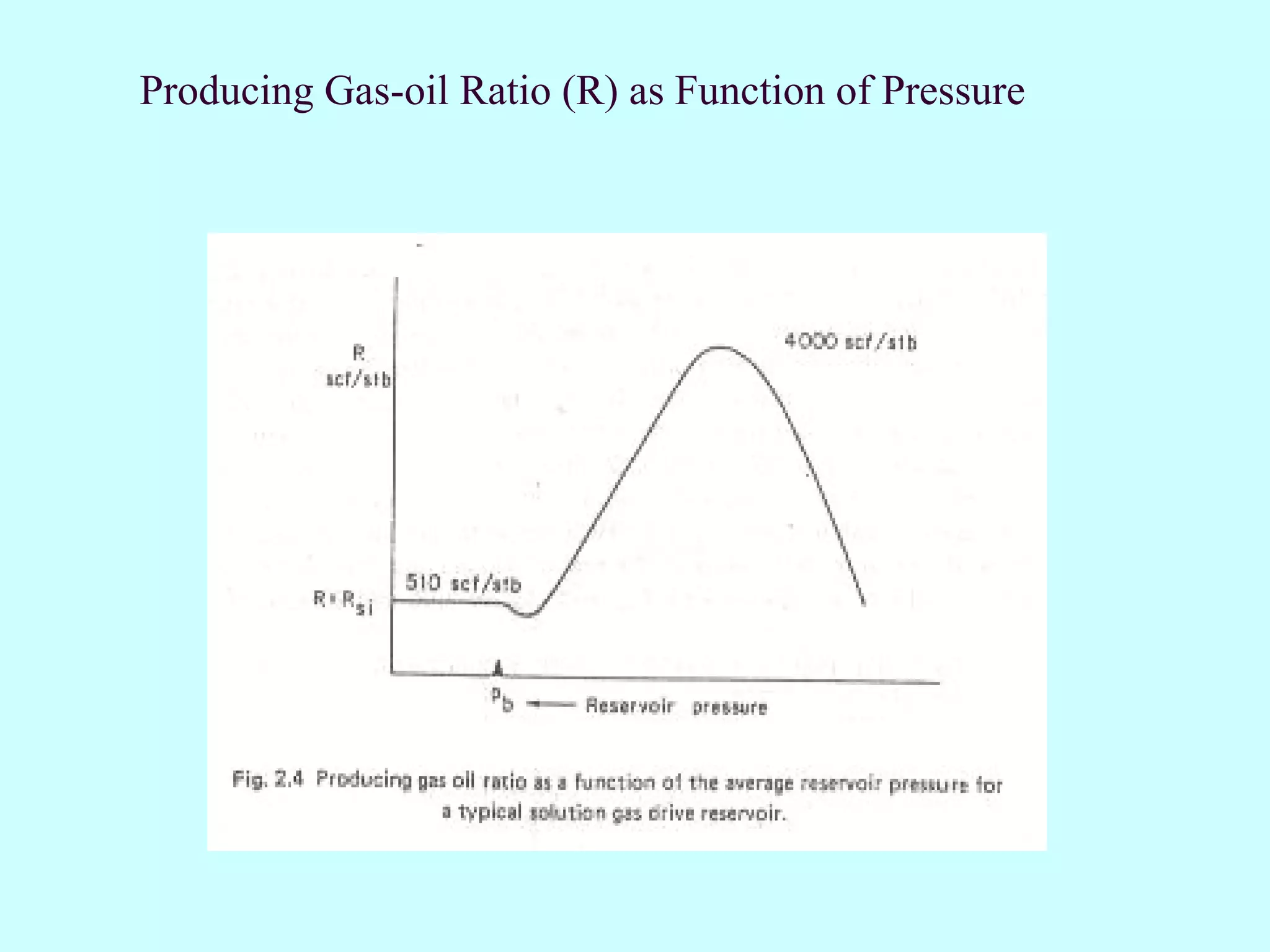
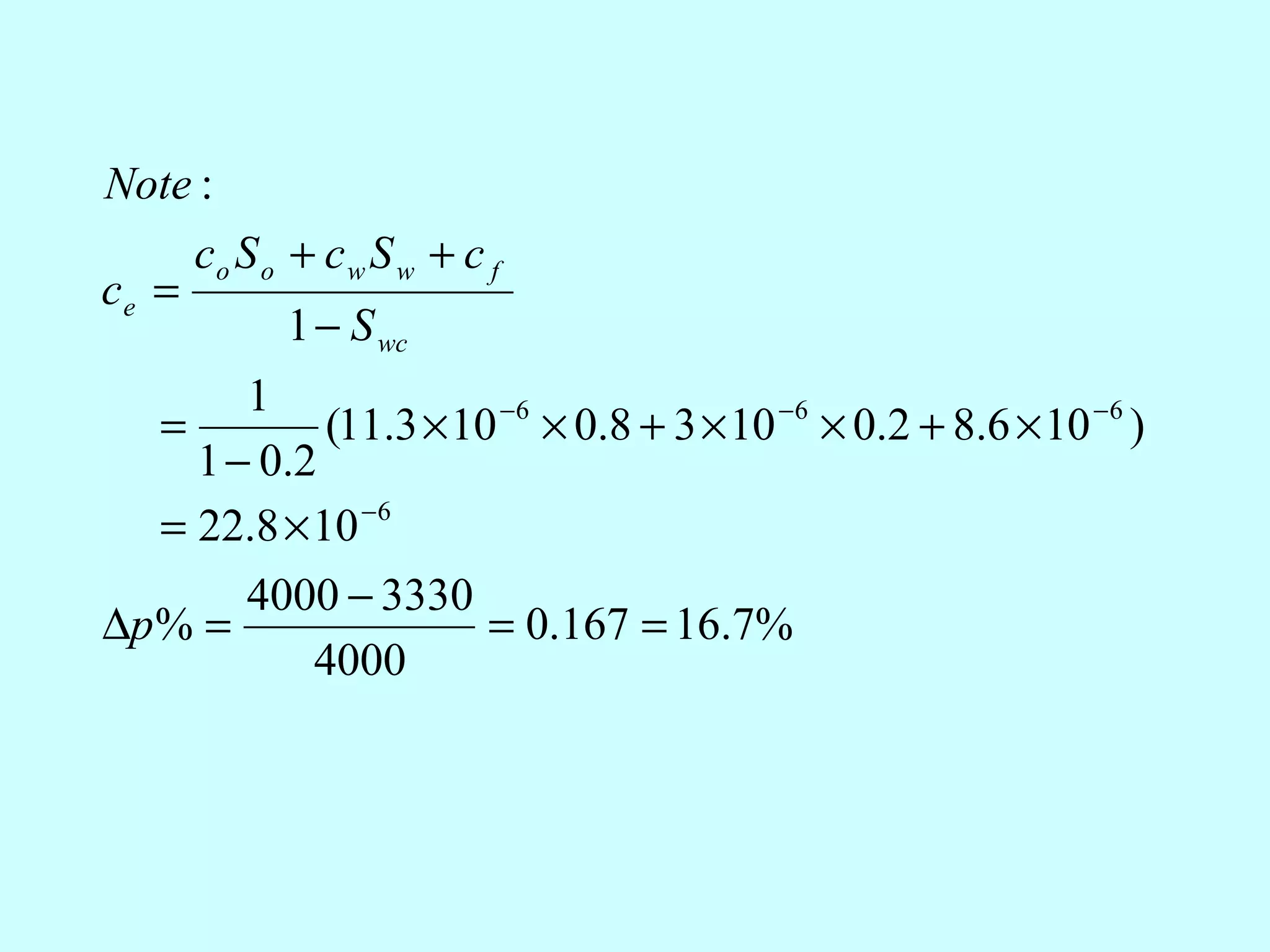
22. Exercise3.2 Solution gas drive; below bubble point pressure
Reservoir-described in exercise 3.1
Pabandon = 900psia
(1) R.F = f(Rp)? Conclusion?
(2) Sg(free gas) = F(Pabandon)?
Solution:
(1) From eq(3.7)
 ( Bo − Boi ) + ( R si − R s ) B g  Bg   c w S wc + c f  
N p [ Bo + ( R p − Rs ) B g ] = NBoi  + m − 1 + (1 + m)
 1− S
∆ p

 Boi B 
  gi   wc   
+ (We − W p ) B w  (3.7)
for solution gas below B.P.
−m =0 no initial gas cap
− We = 0 ; W p = 0
c w S wc + c f
− NBoi ( )∆p is negligible if S g is developed
1 − S wc

23. Eq(3.7) becomes
N p [ Bo + ( R p − Rs ) B g ] = N [( Bo − Boi ) + ( Rsi − Rs ) B g ] (3.20)
Np ( Bo − Boi ) + ( Rsi − Rs ) B g
R.F . = =
N Bo + ( R p − R s ) B g
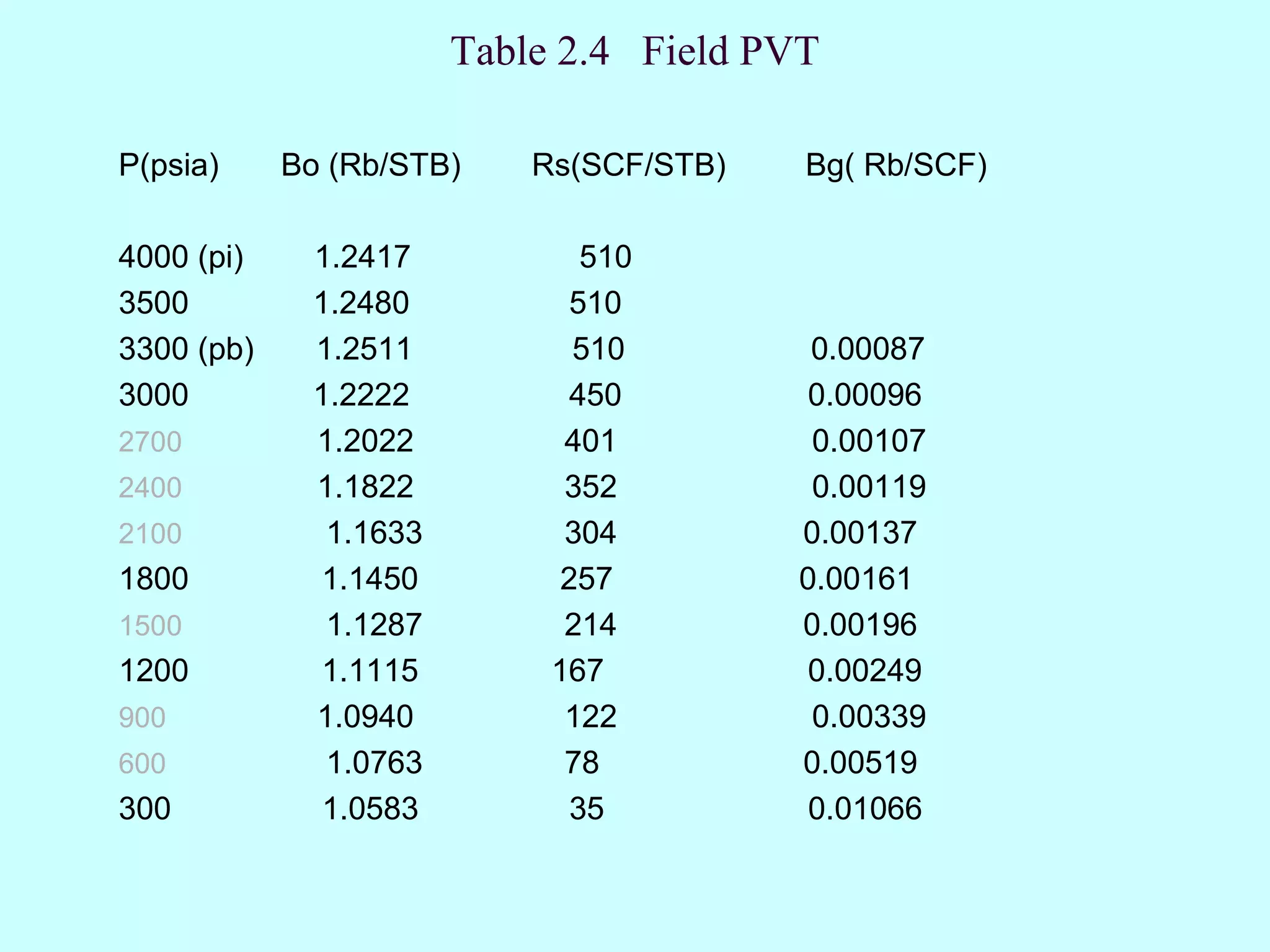
Np (1.0940 − 1.2417) + (510 − 122) × 0.00339 344
R.F . p =900 = = =
N p =900
1.0940 + ( R p − 122) × 0.00339 R p + 201
1
Conclusion: RF ≈
Rp
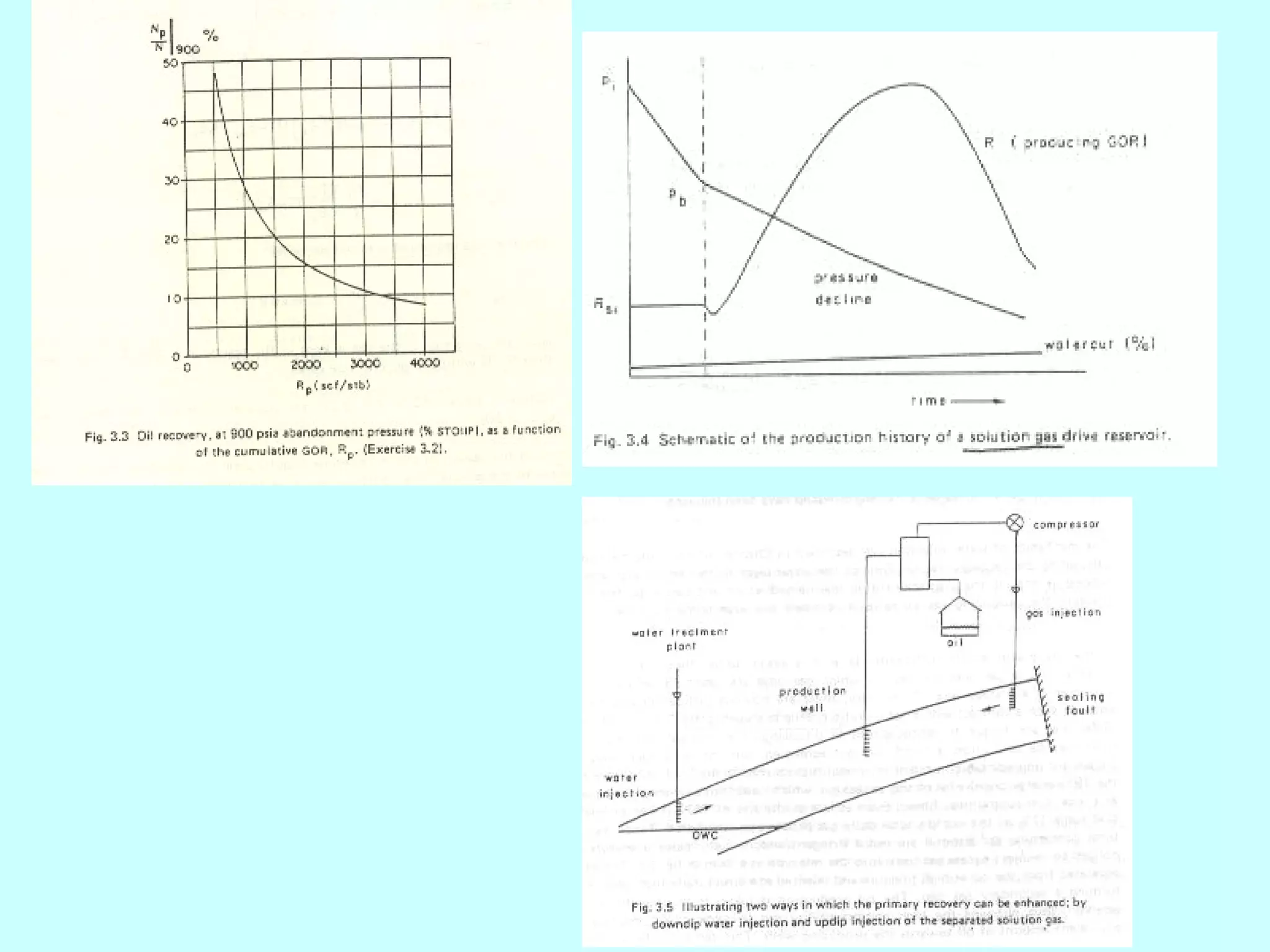
From Fig .3.3 ( p.55)
Np
R p = 500 SCF ⇒ = 49% = 0.49
STB N 900

25. (2) the overall gas balance
liberated total gas gas still
gas in the = amount −
− produced dissolved
reservoir of gas at surface in the oil
NBoi HCPV
= pore volume = for p > p b
1 − S wc (1 − S wc )
NBoi S g
⇒ = NR si B g − N p R p B g − ( N − N p ) Rs B g
(1 − S wc )
[ N ( Rsi − Rs ) − N p ( R p − Rs )]B g (1 − S wc )
⇒ Sg =  (3.21)
NBoi
Np
[ N ( Rsi − Rs ) − Np( R p − Rs )]Bg (1 − S wc ) [( Rsi − Rs ) − ( R p − Rs )]
Sg = = N Bg (1 − S wc )
NBoi Boi
[(510 − 122) − 0.49(500 − 122)]
= × 0.00339 × 0.8 = 0.4428
1.2417