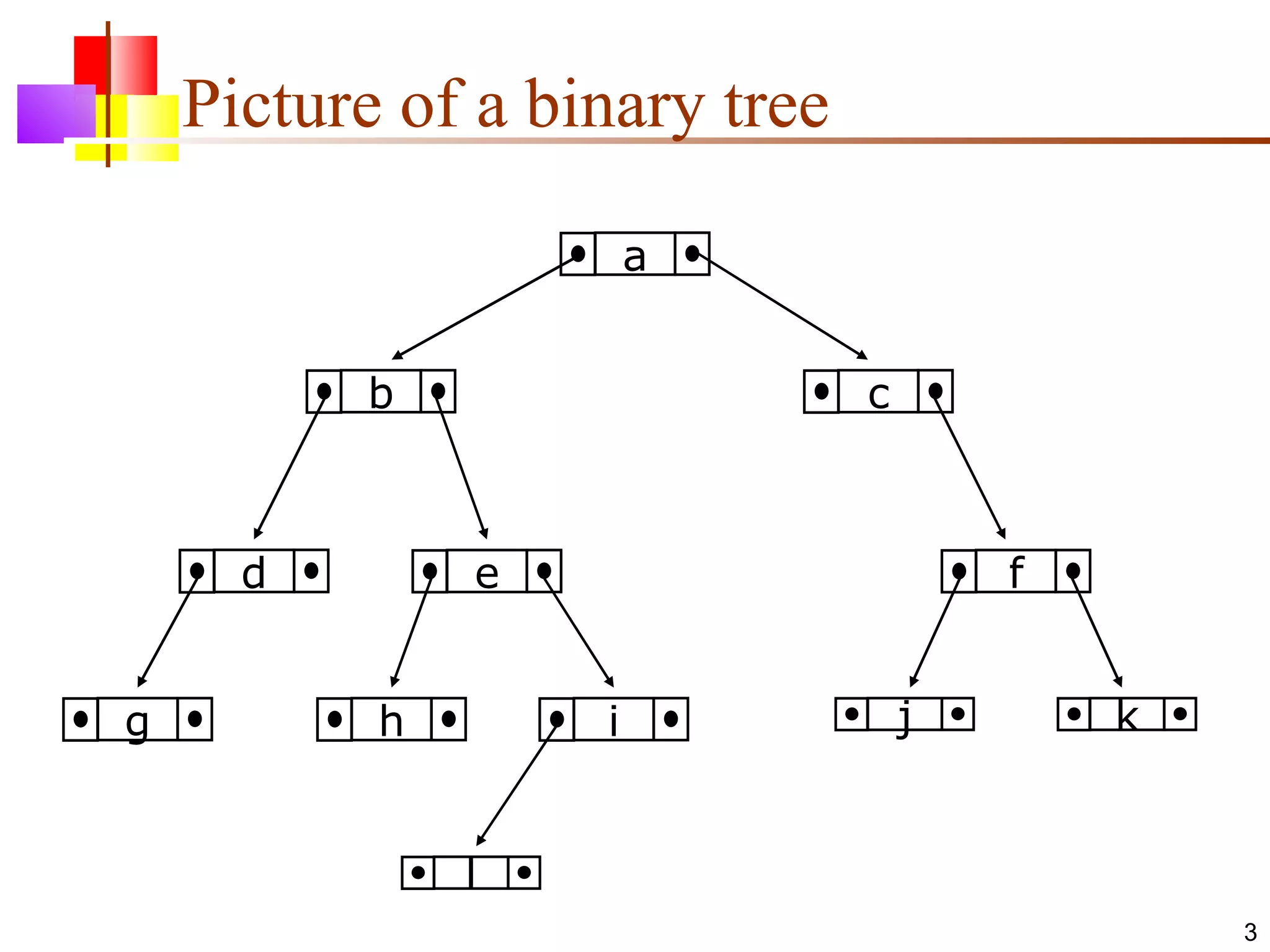
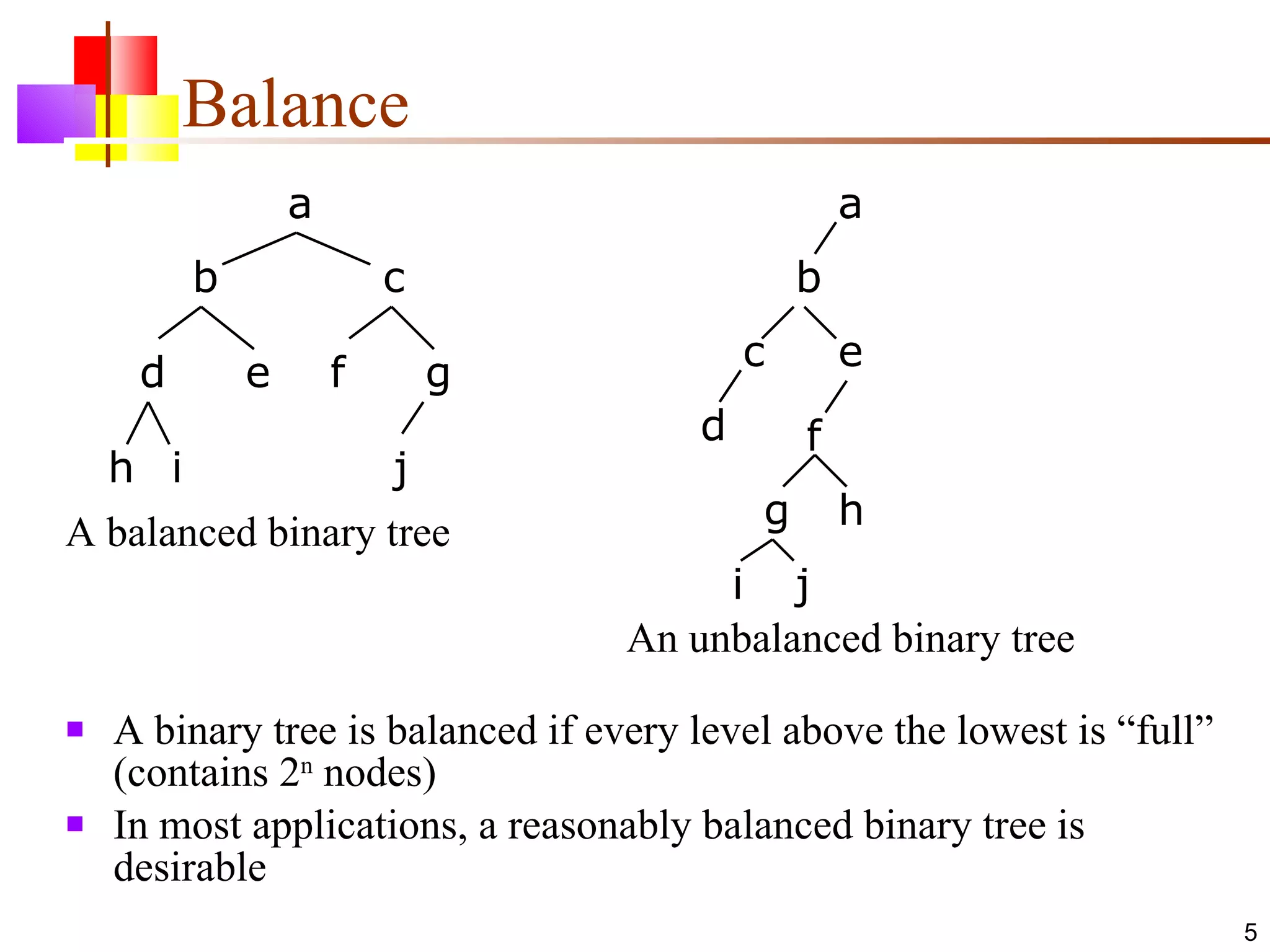
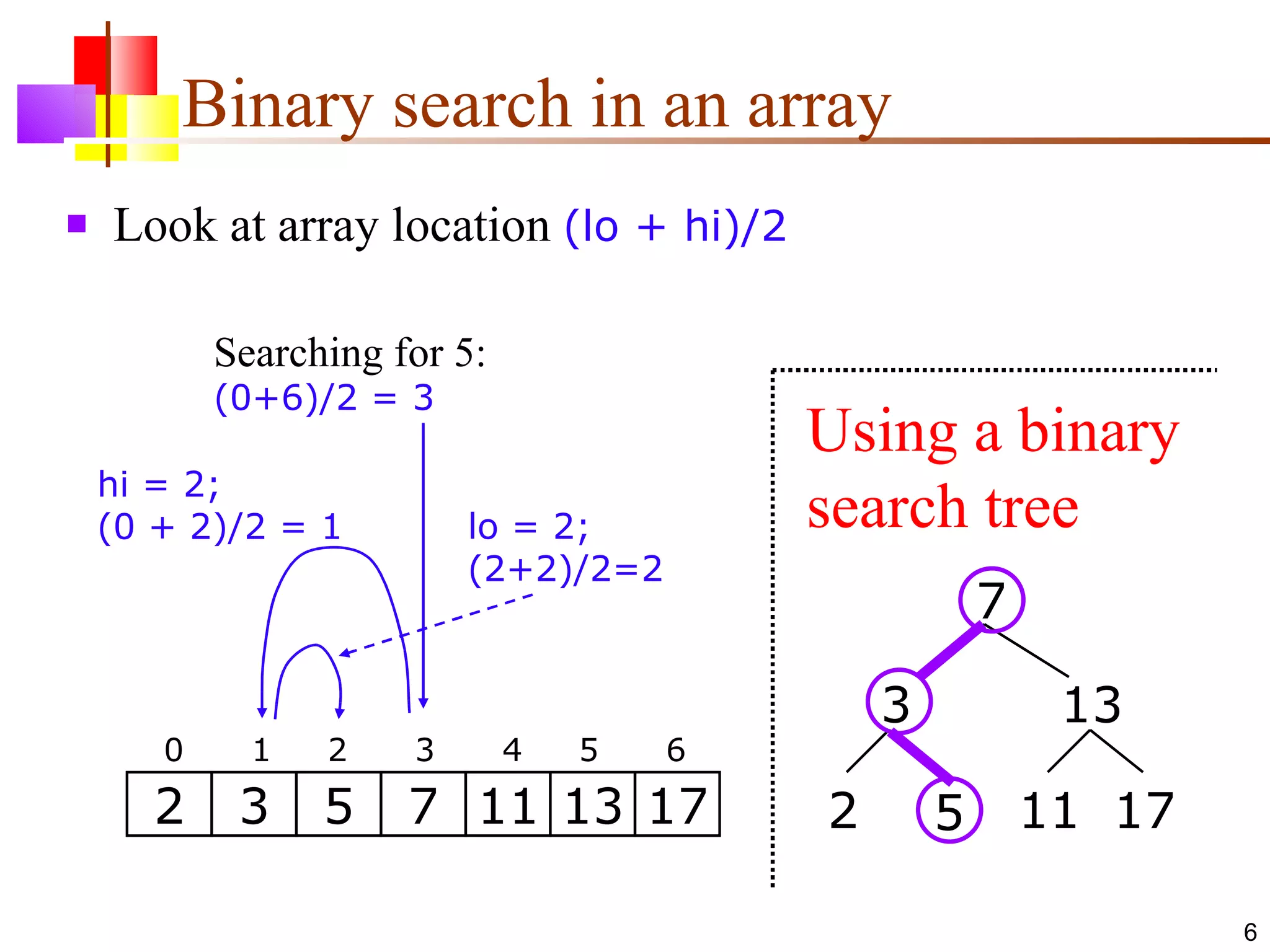
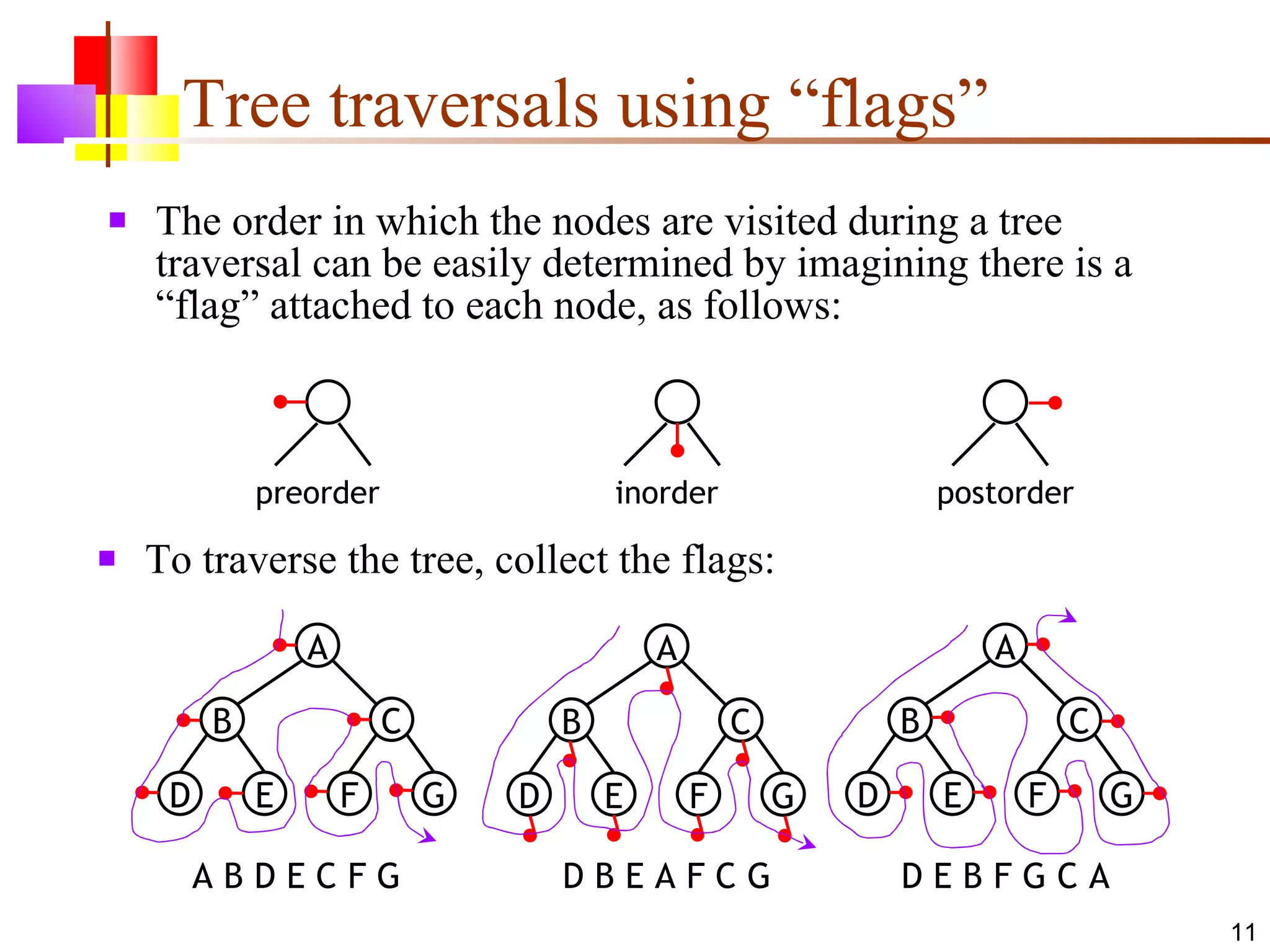
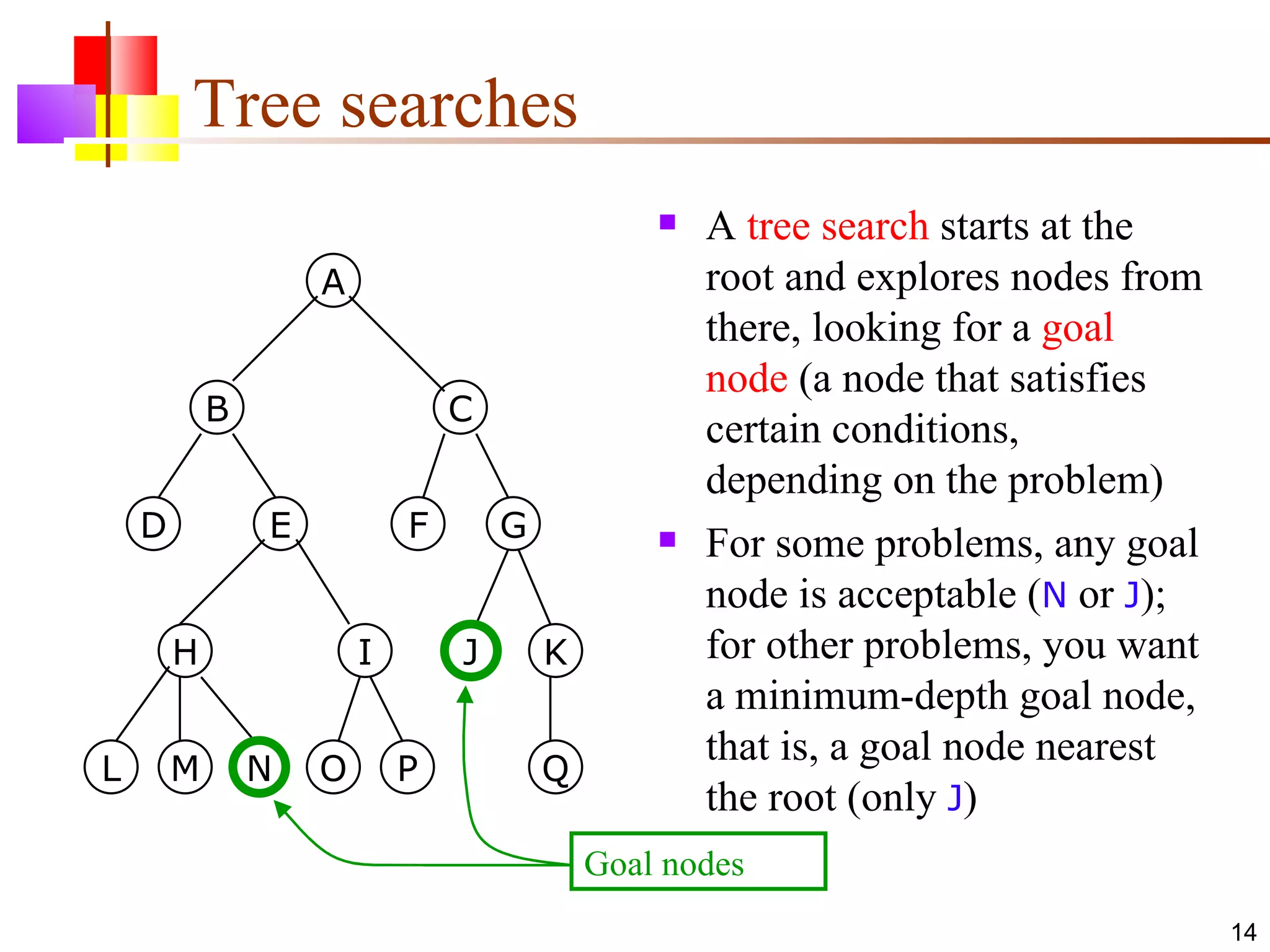
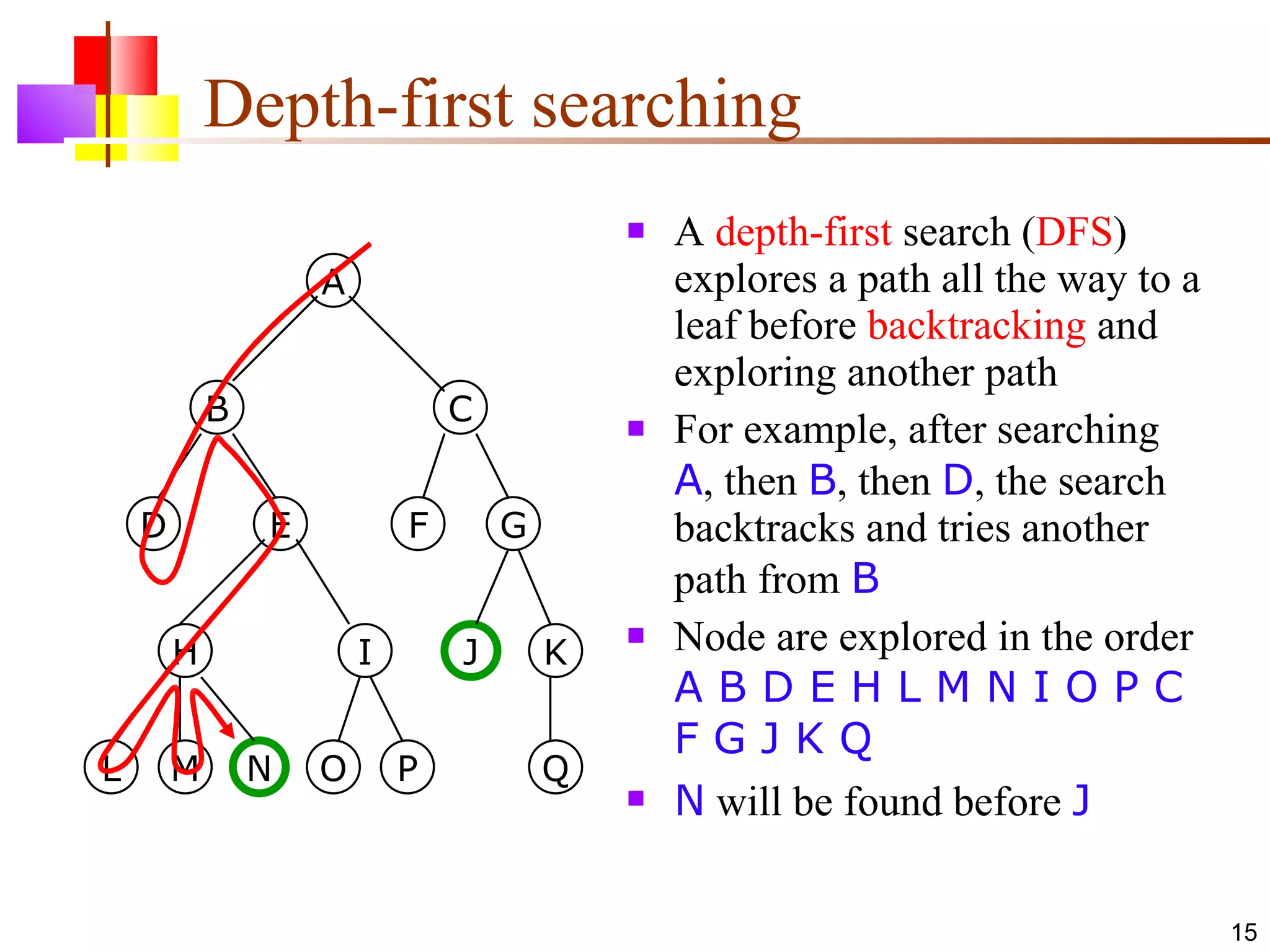
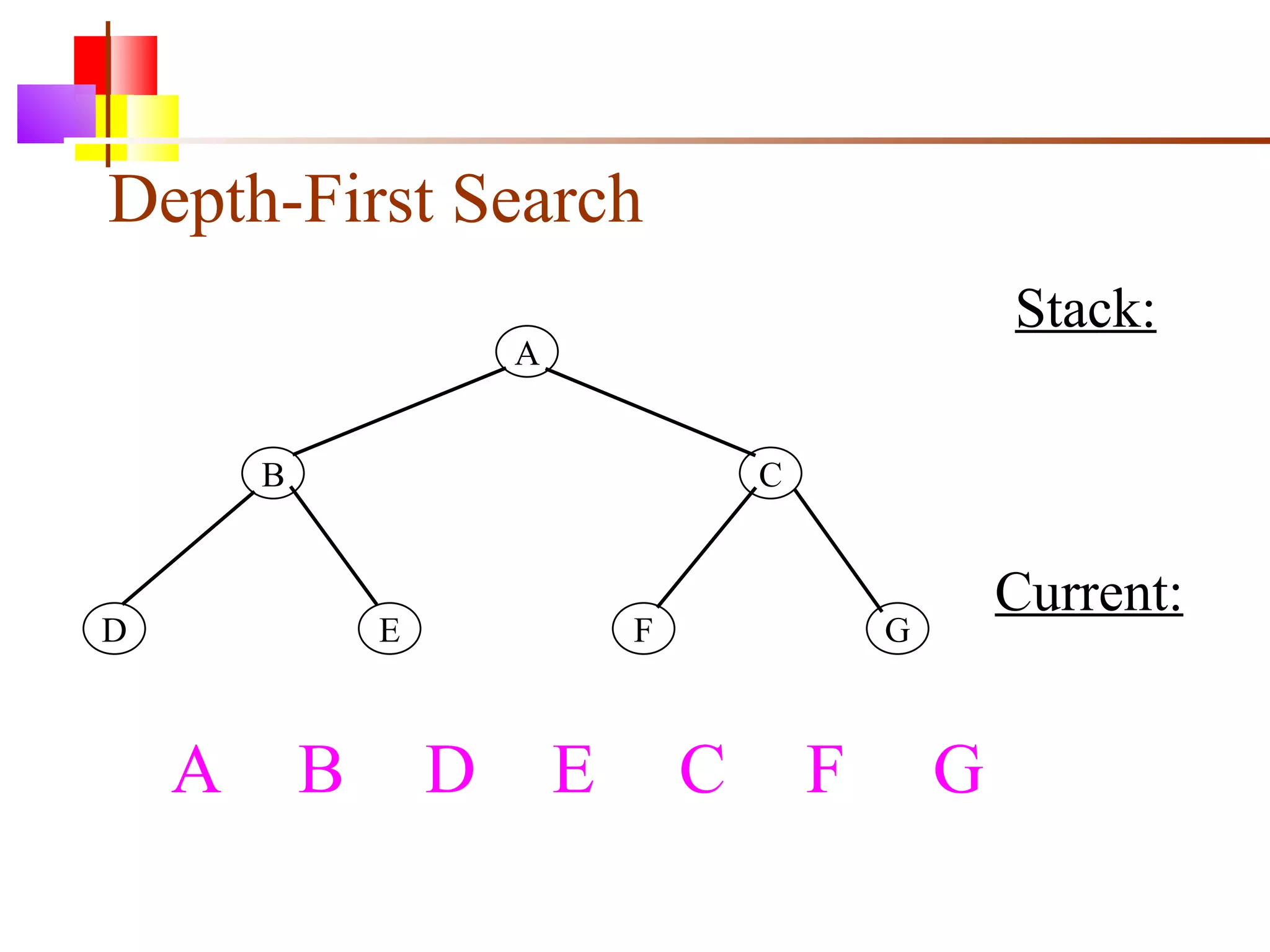
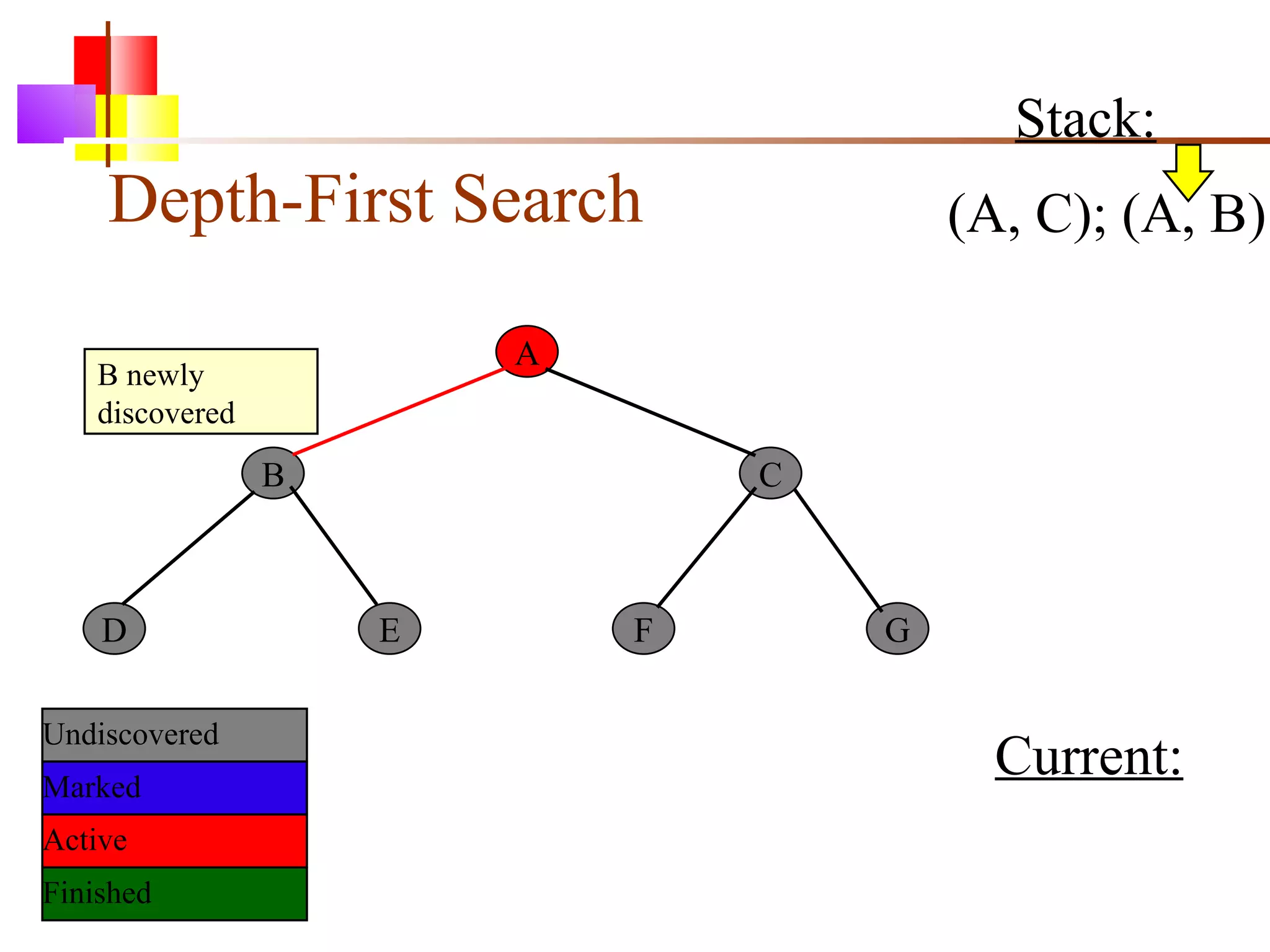
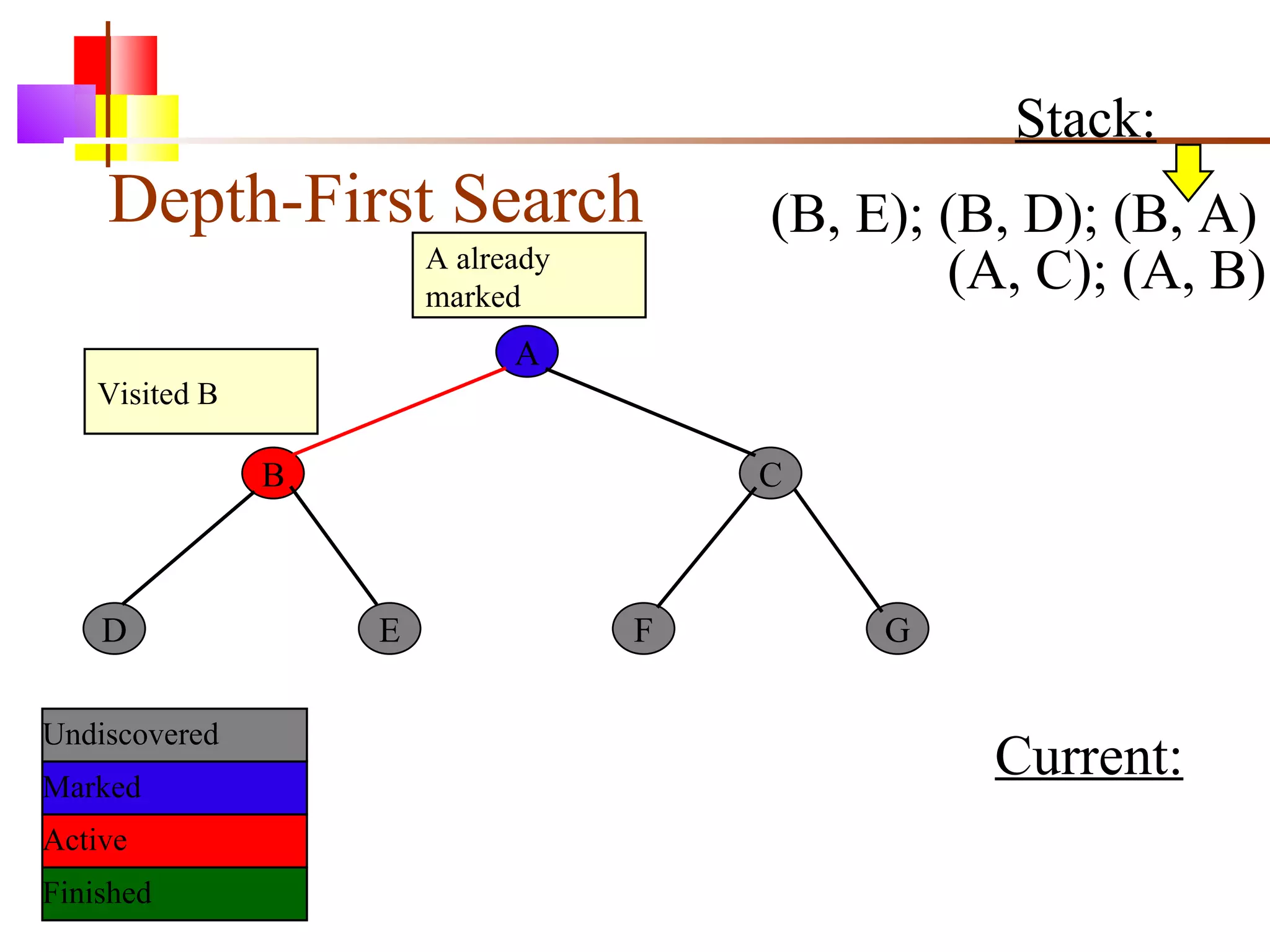
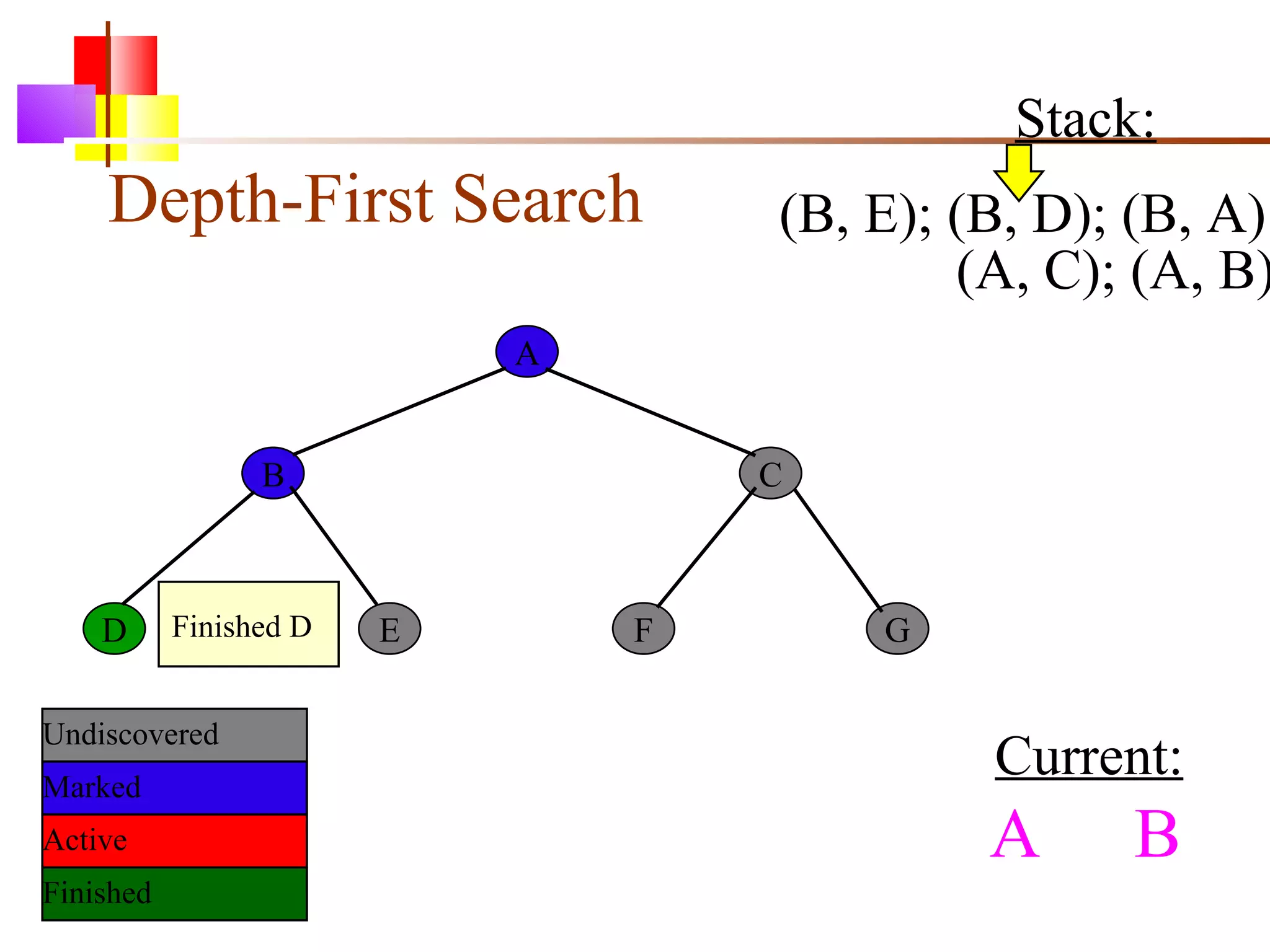
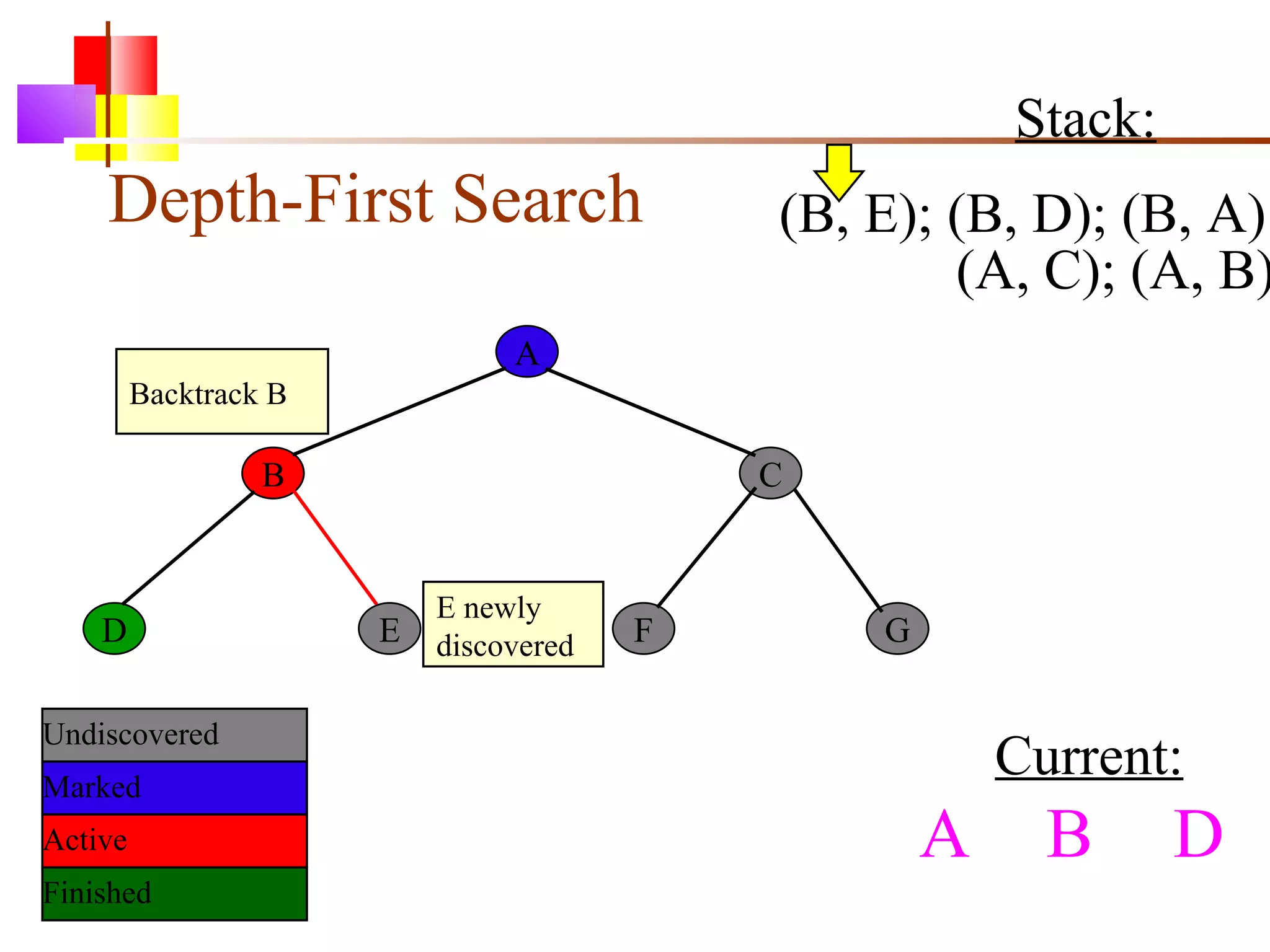
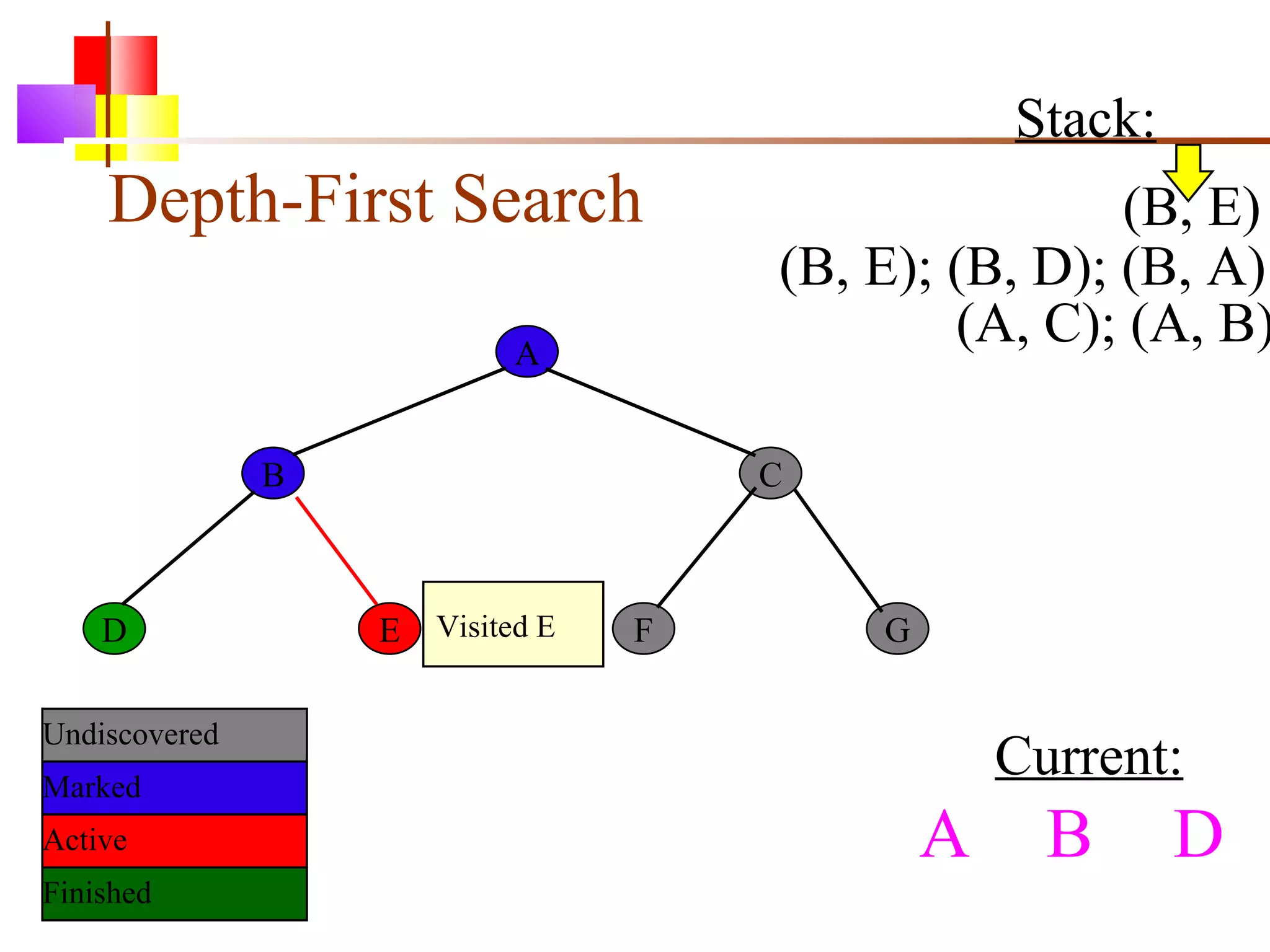
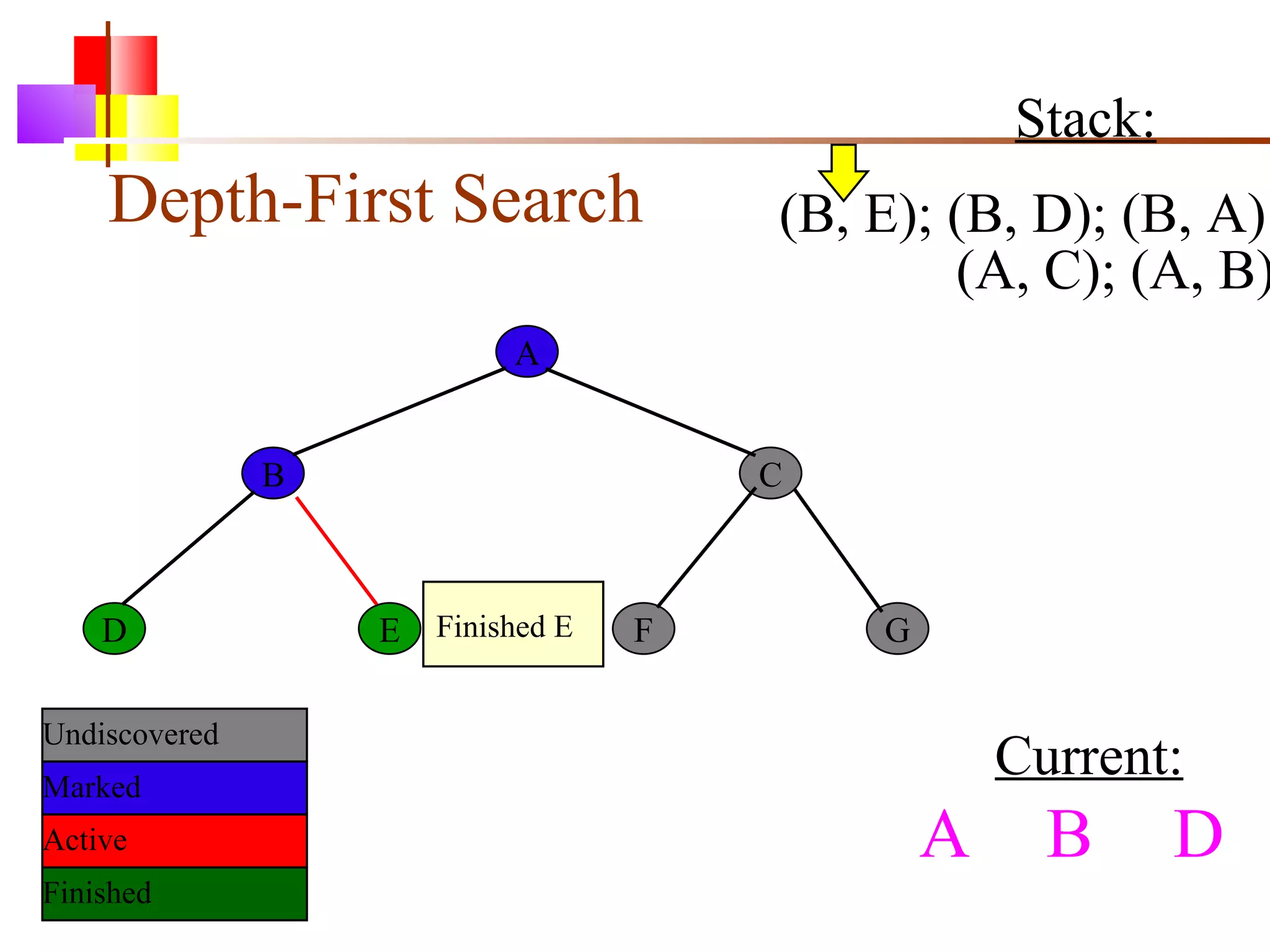
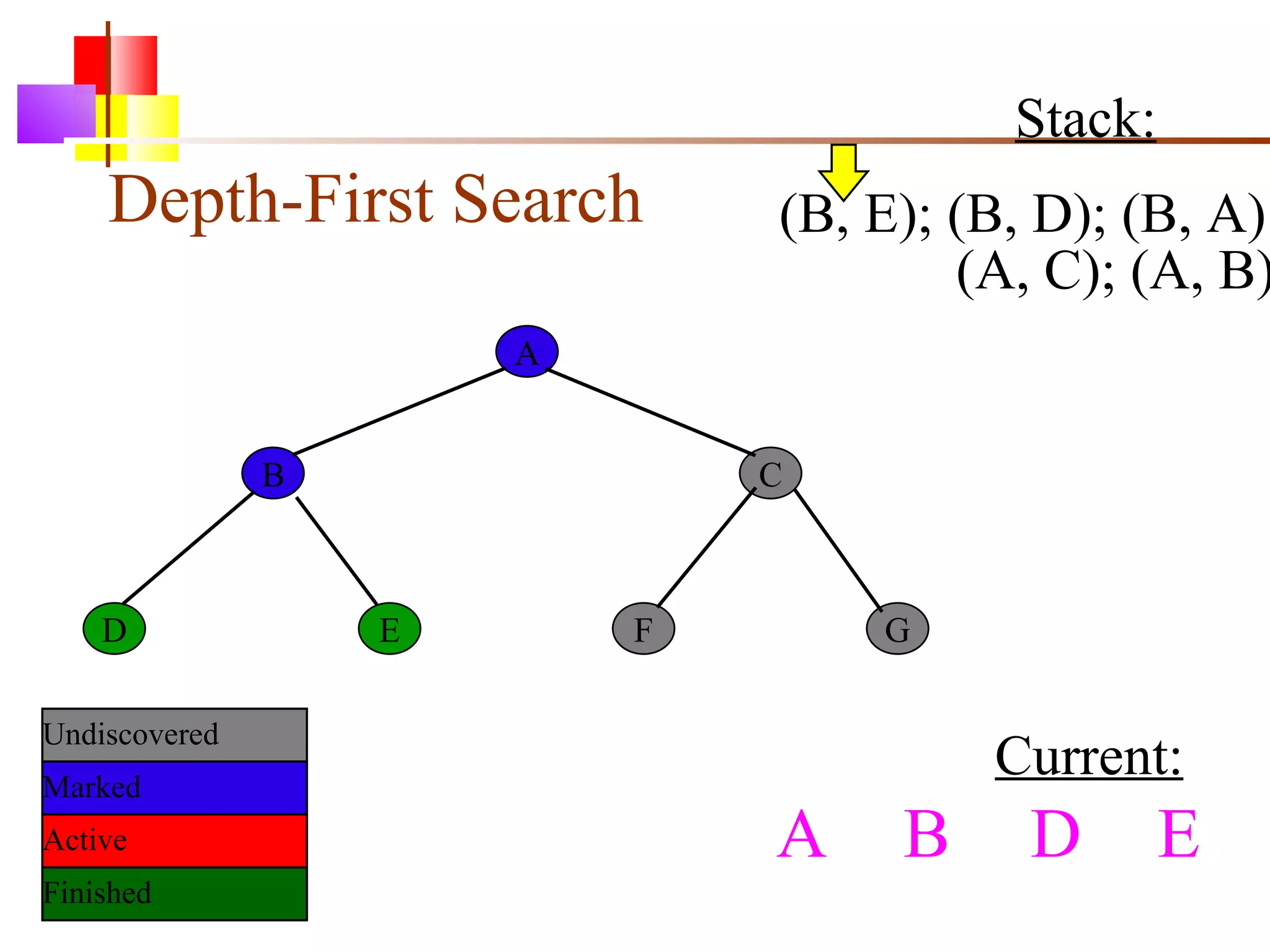
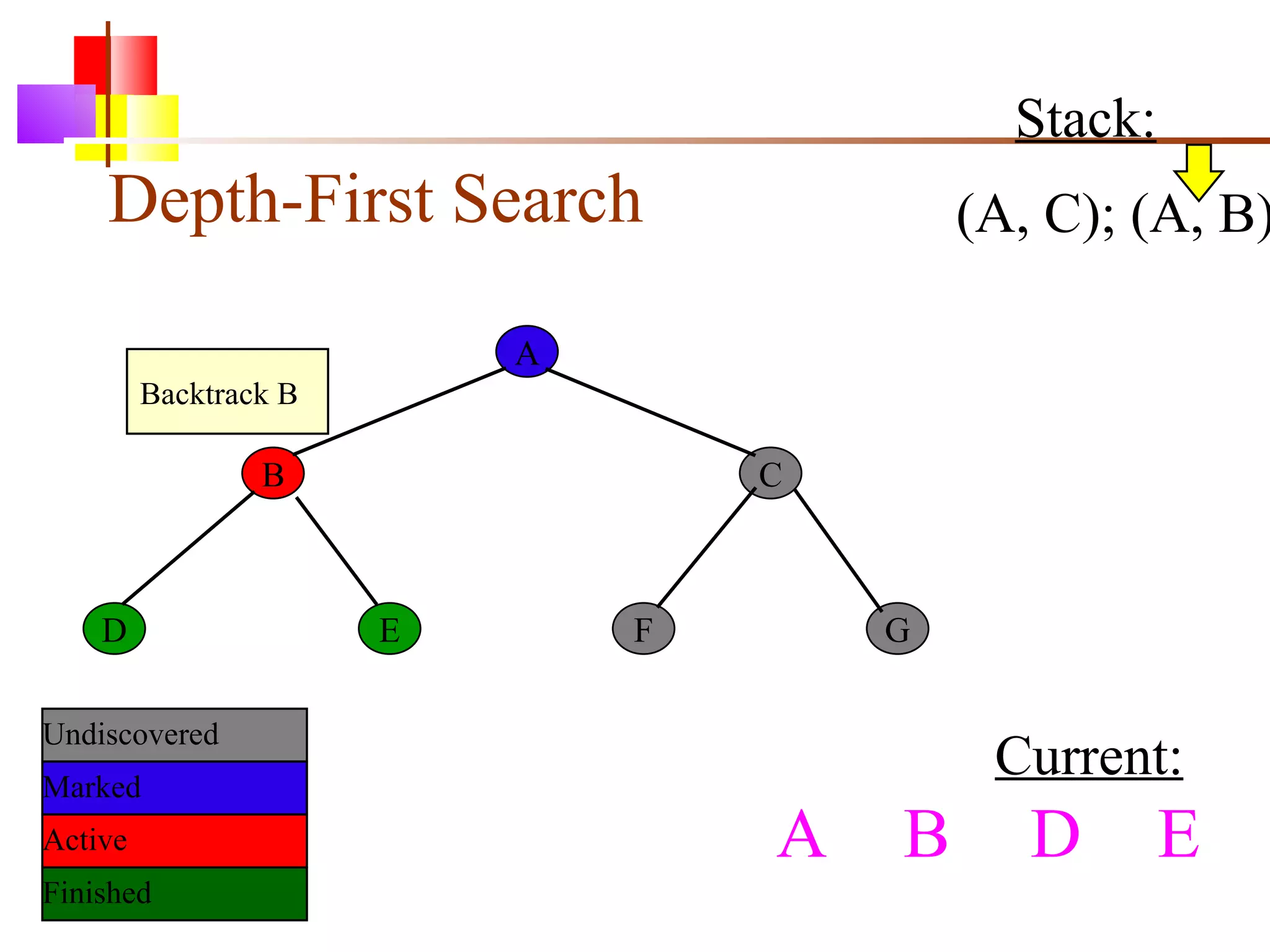
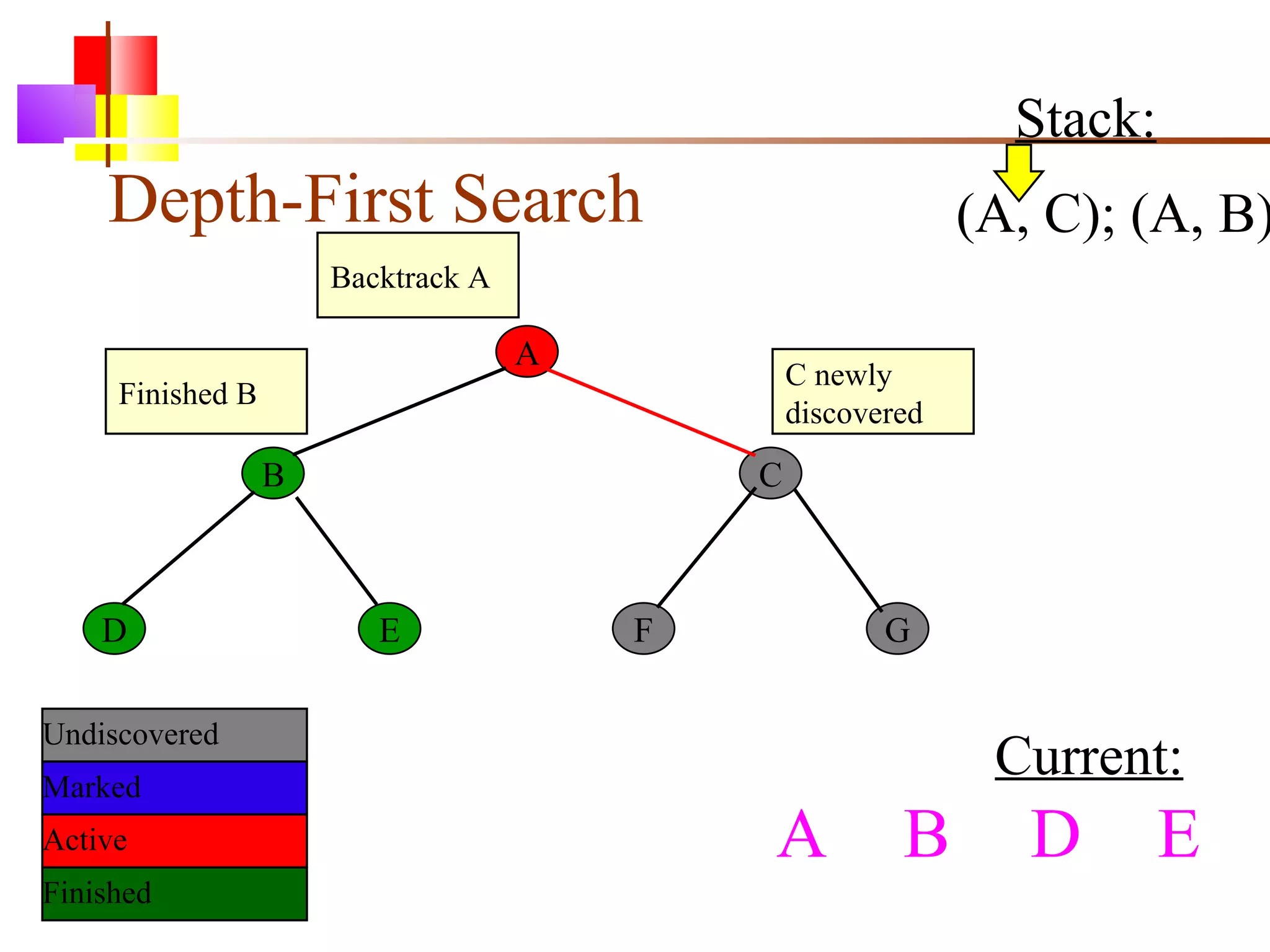
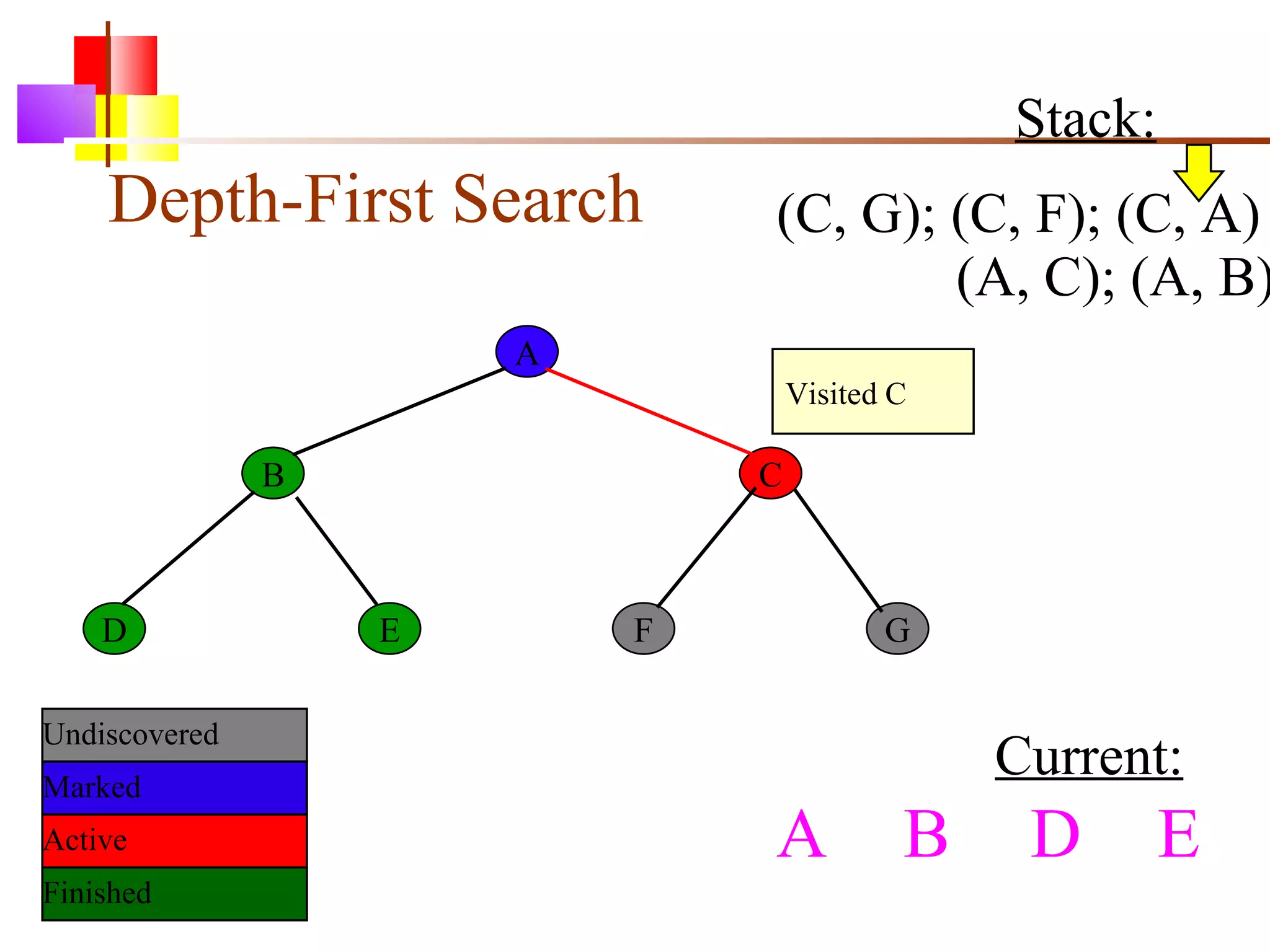
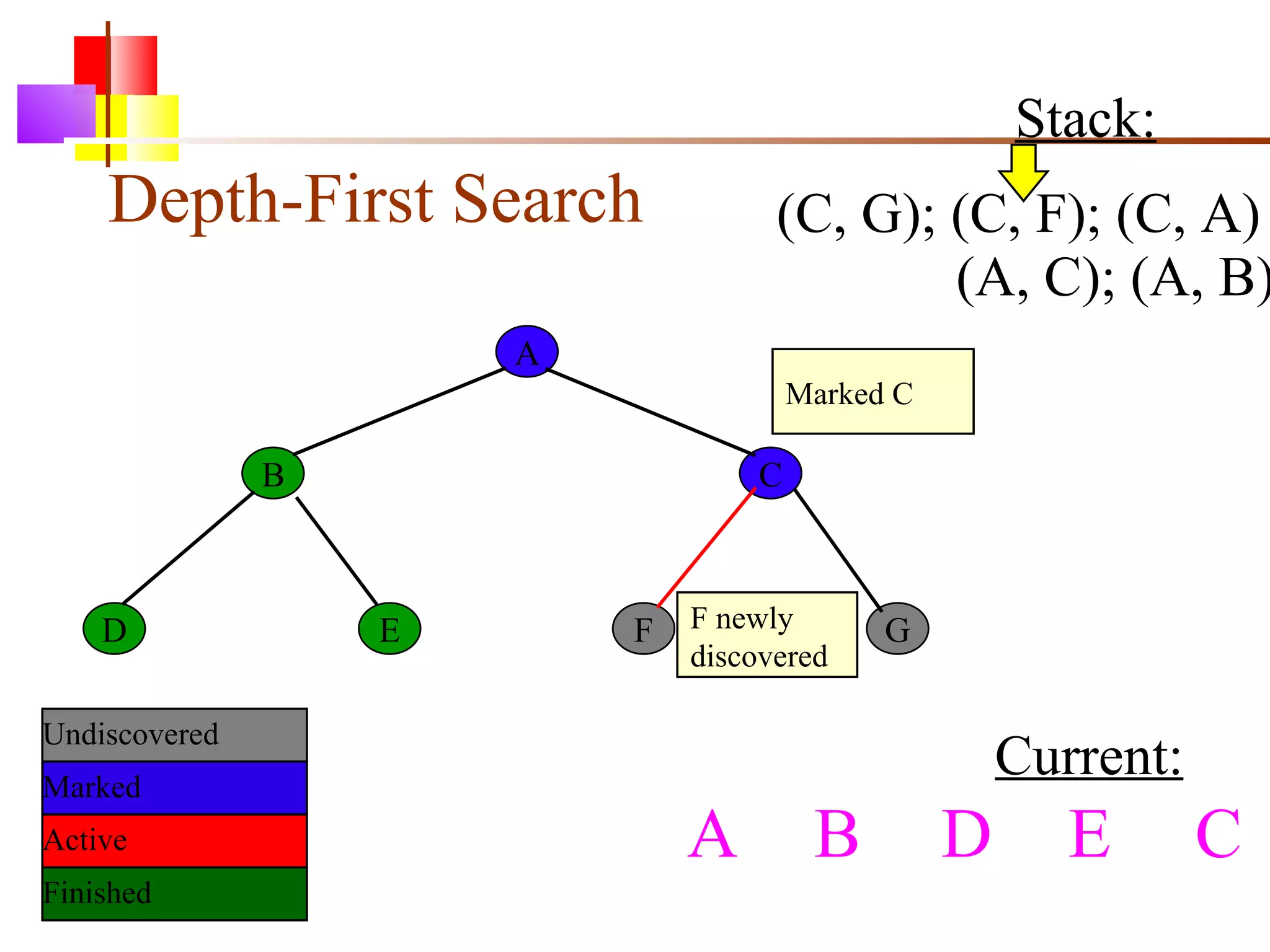
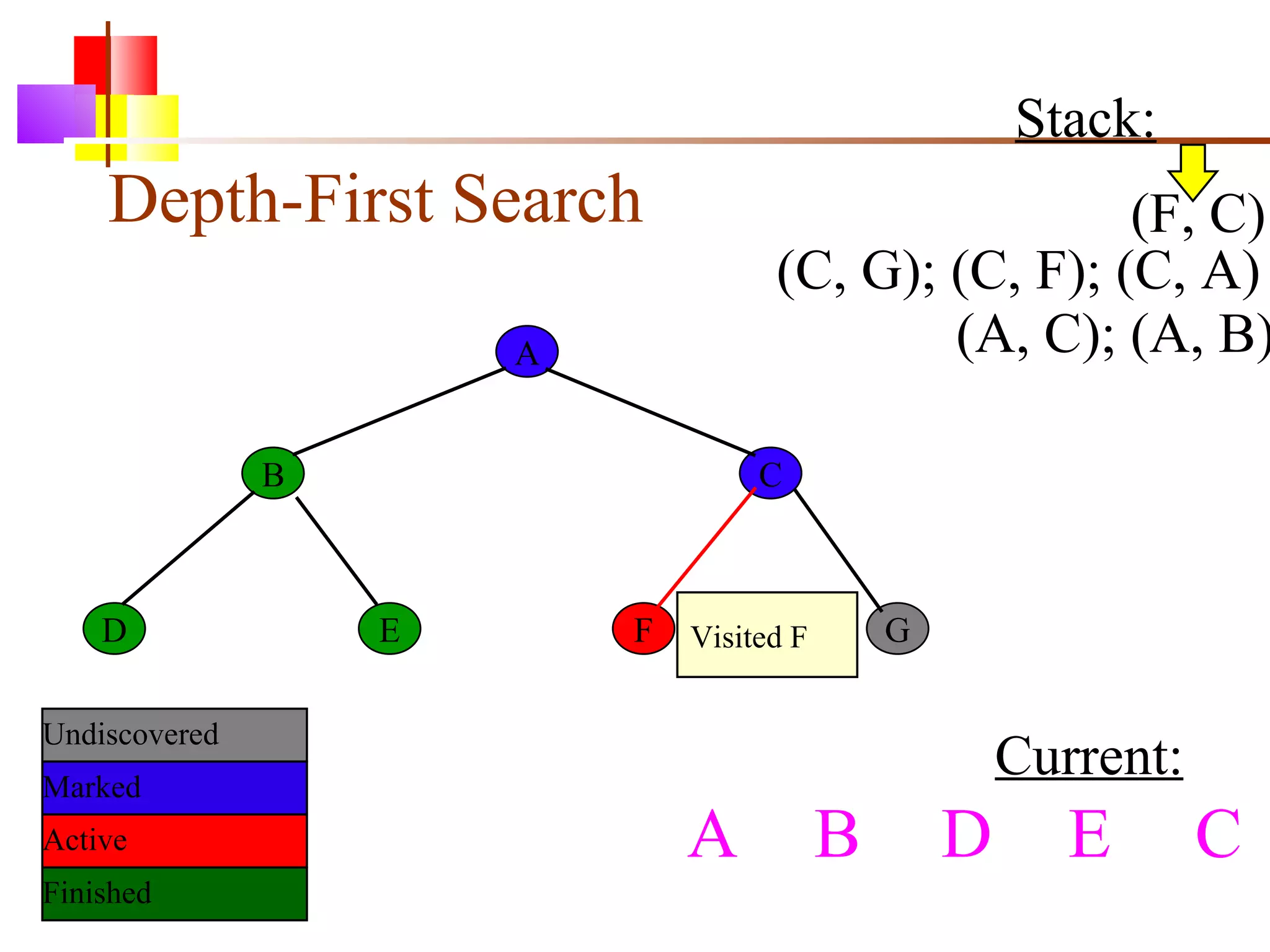
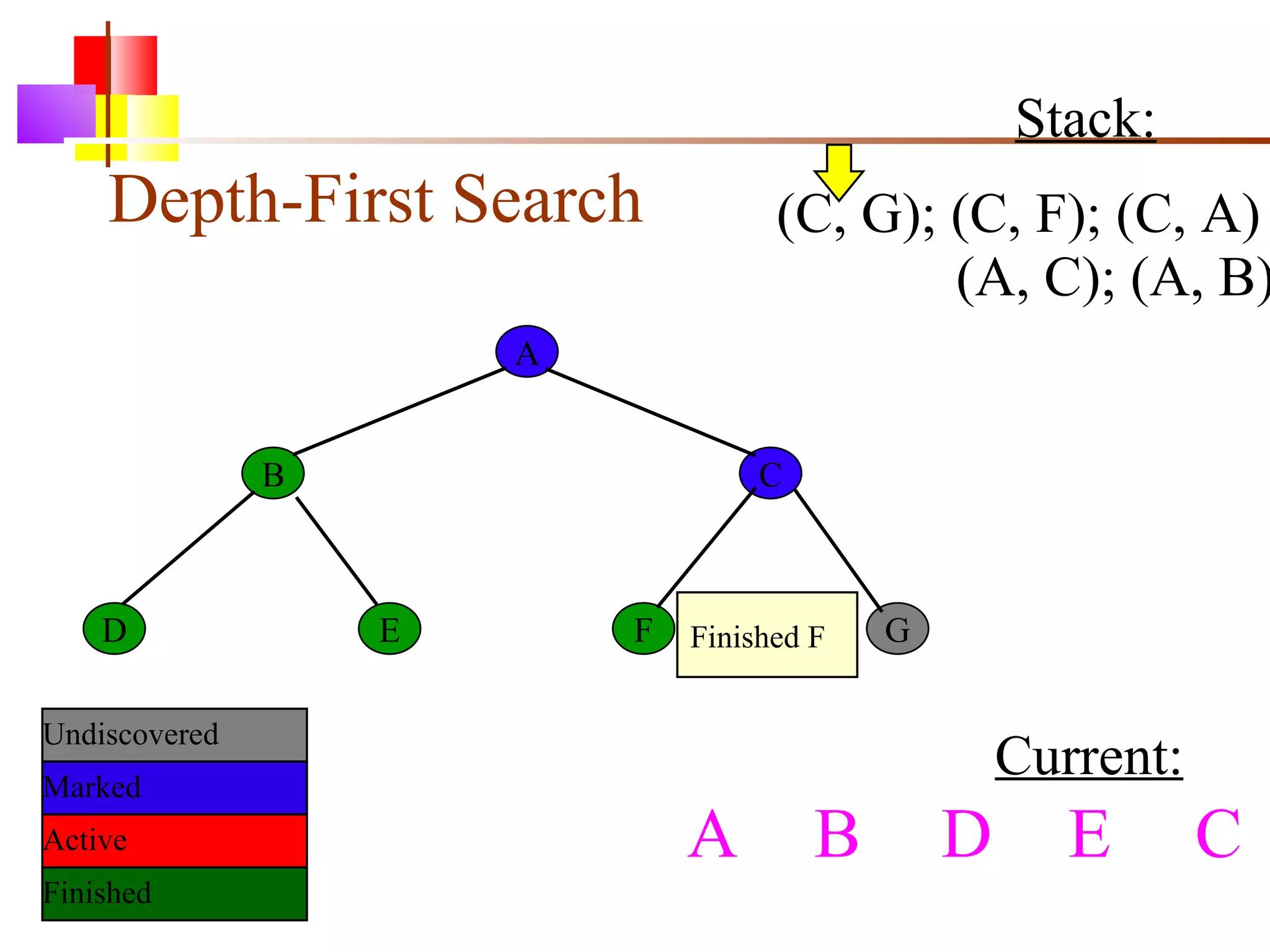
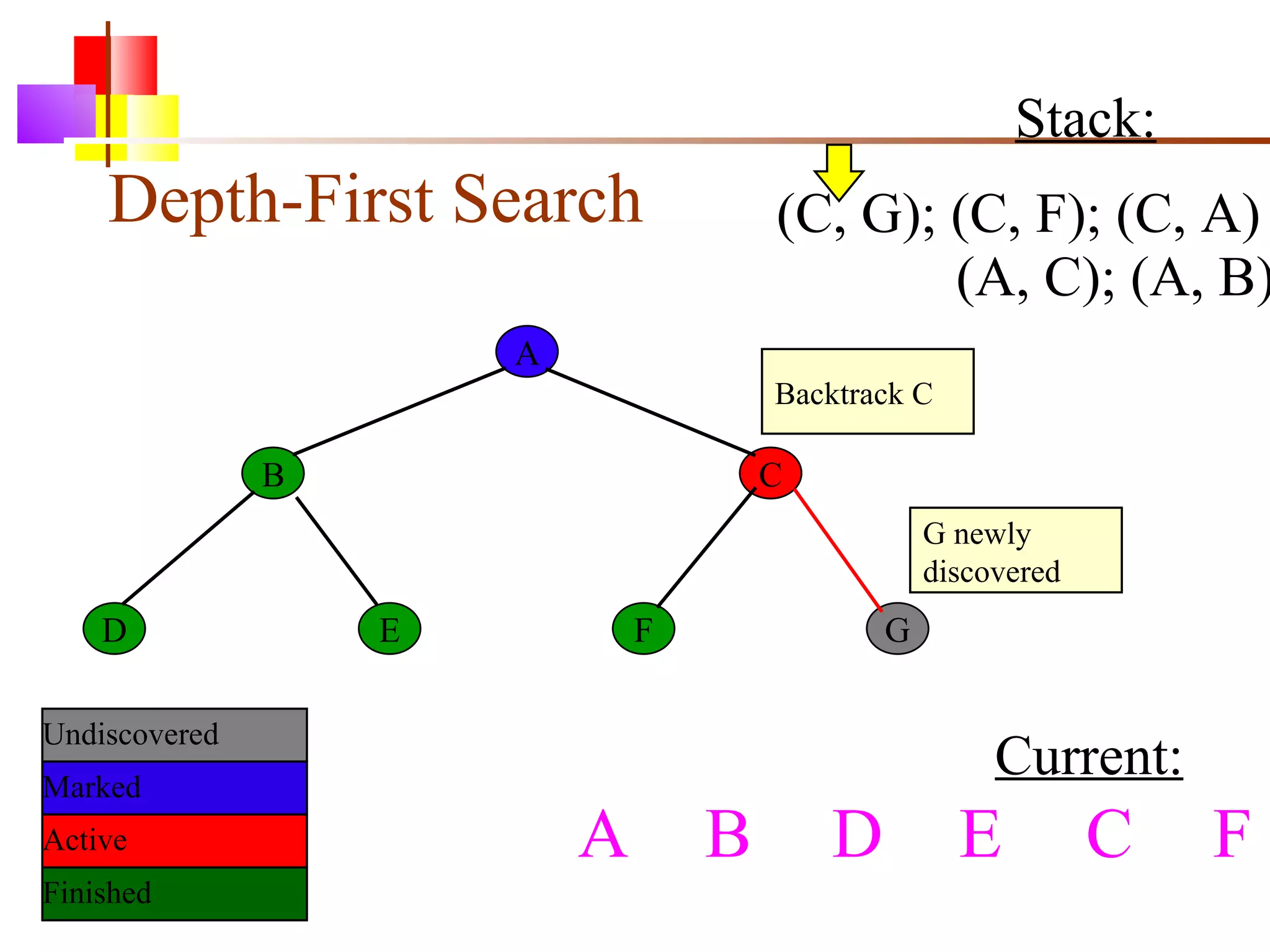
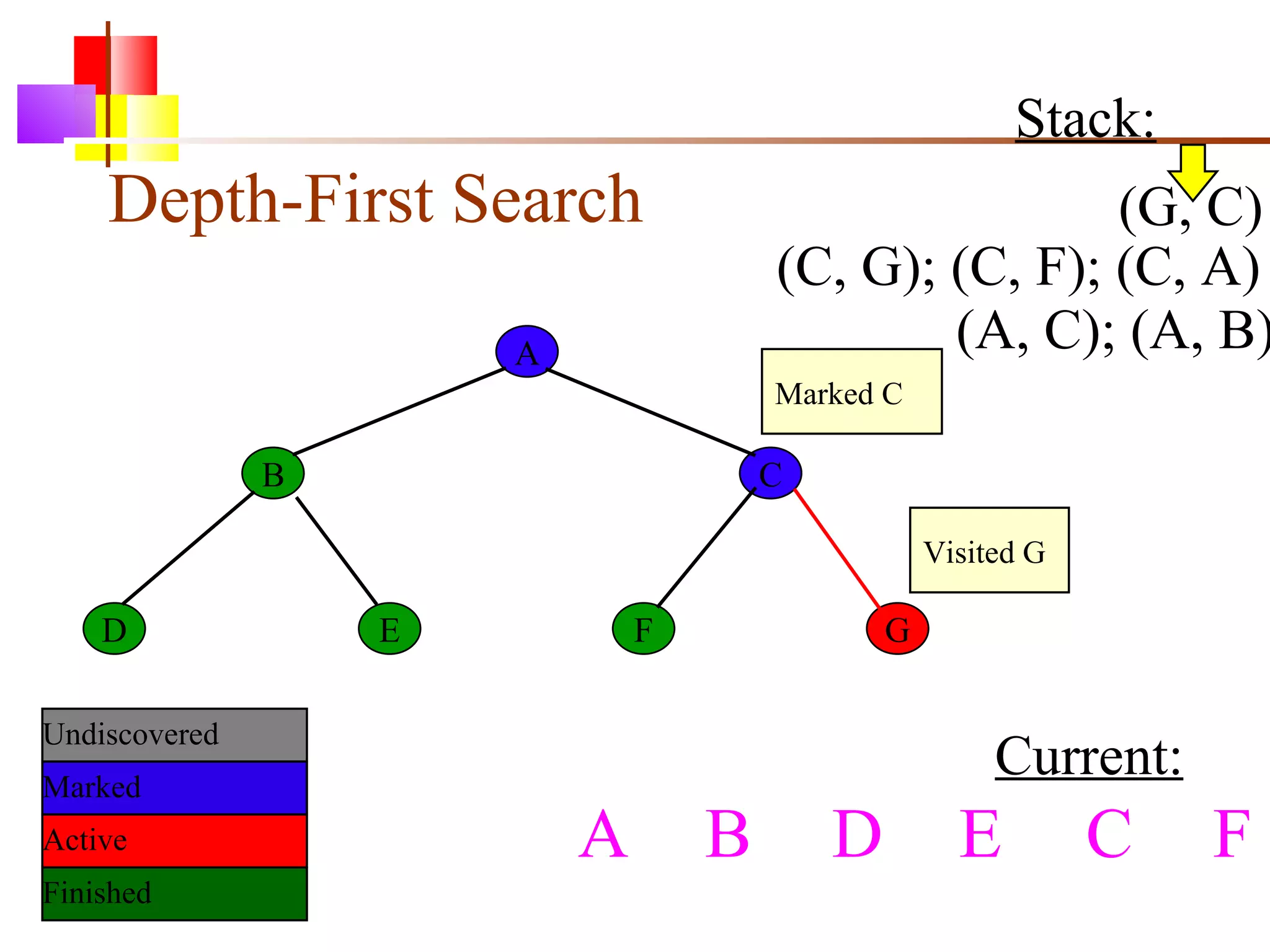
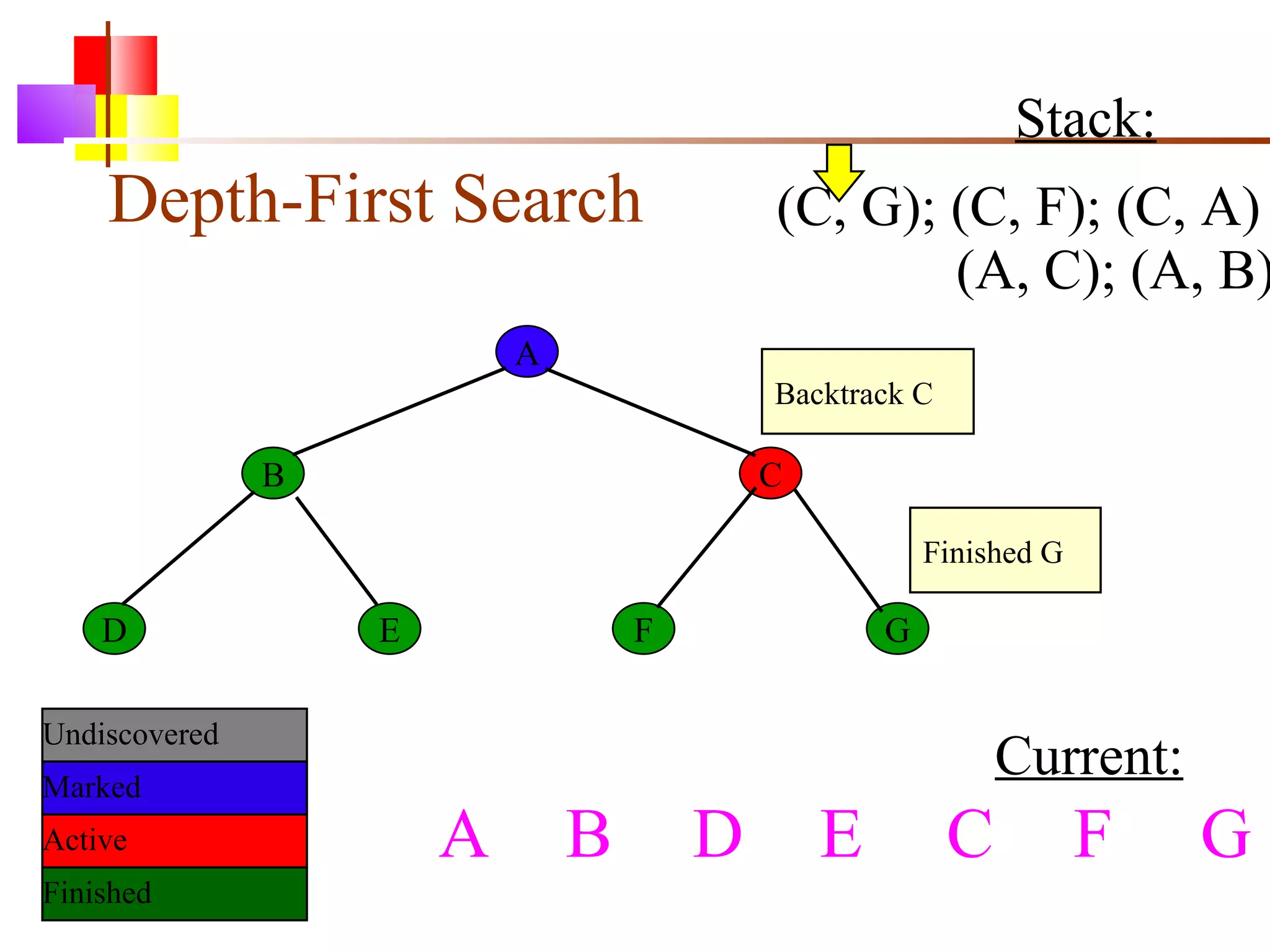
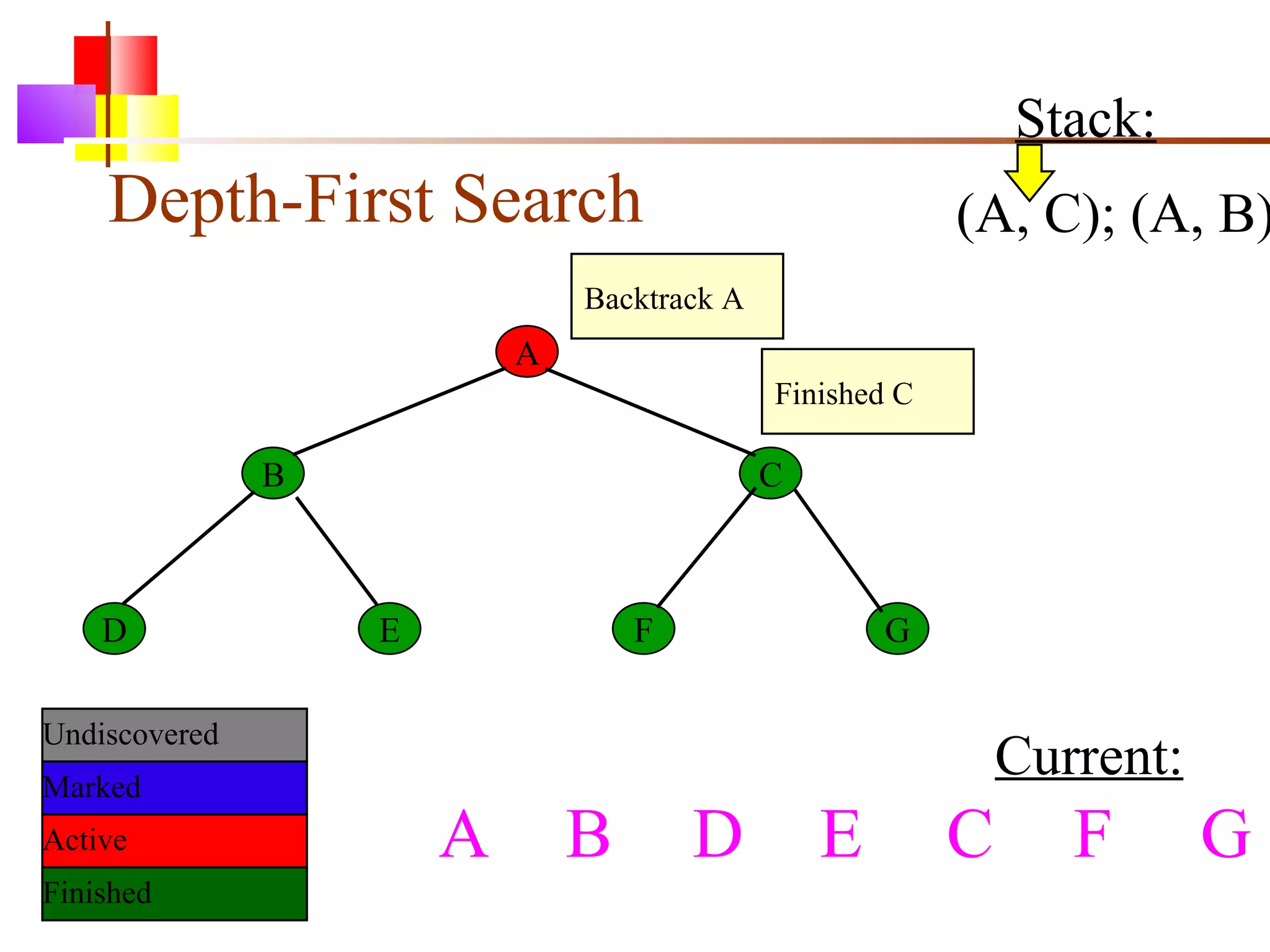
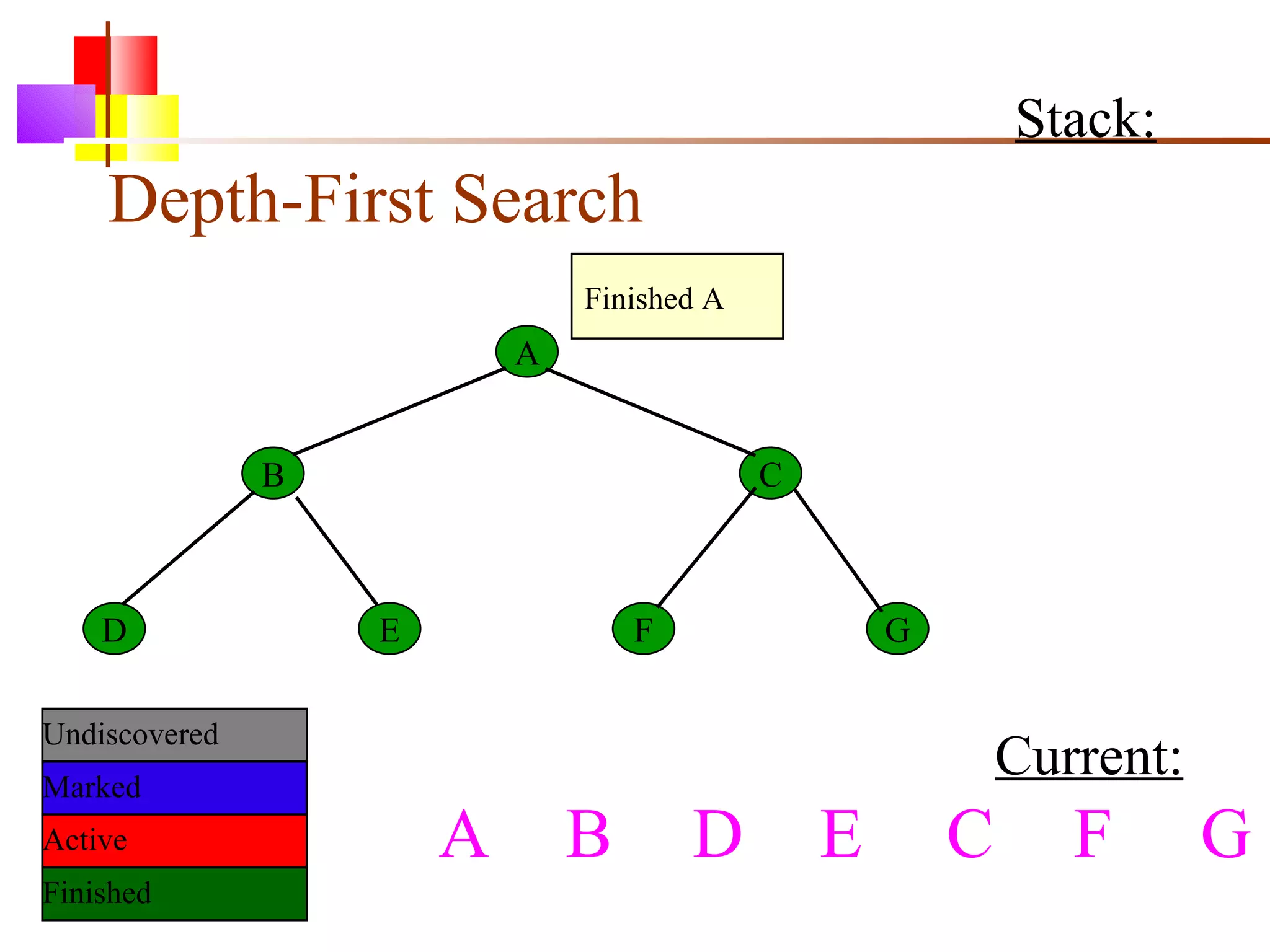
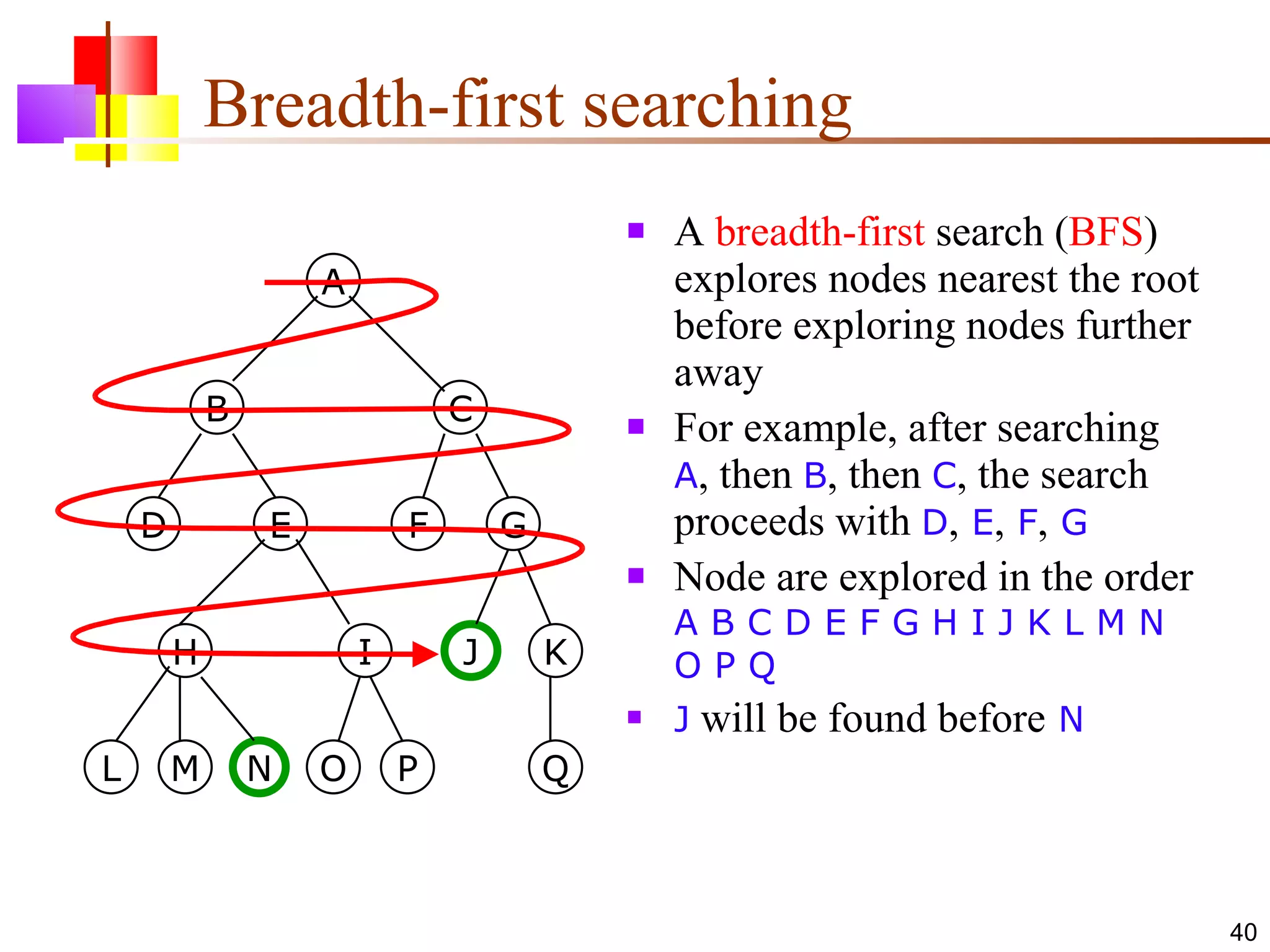
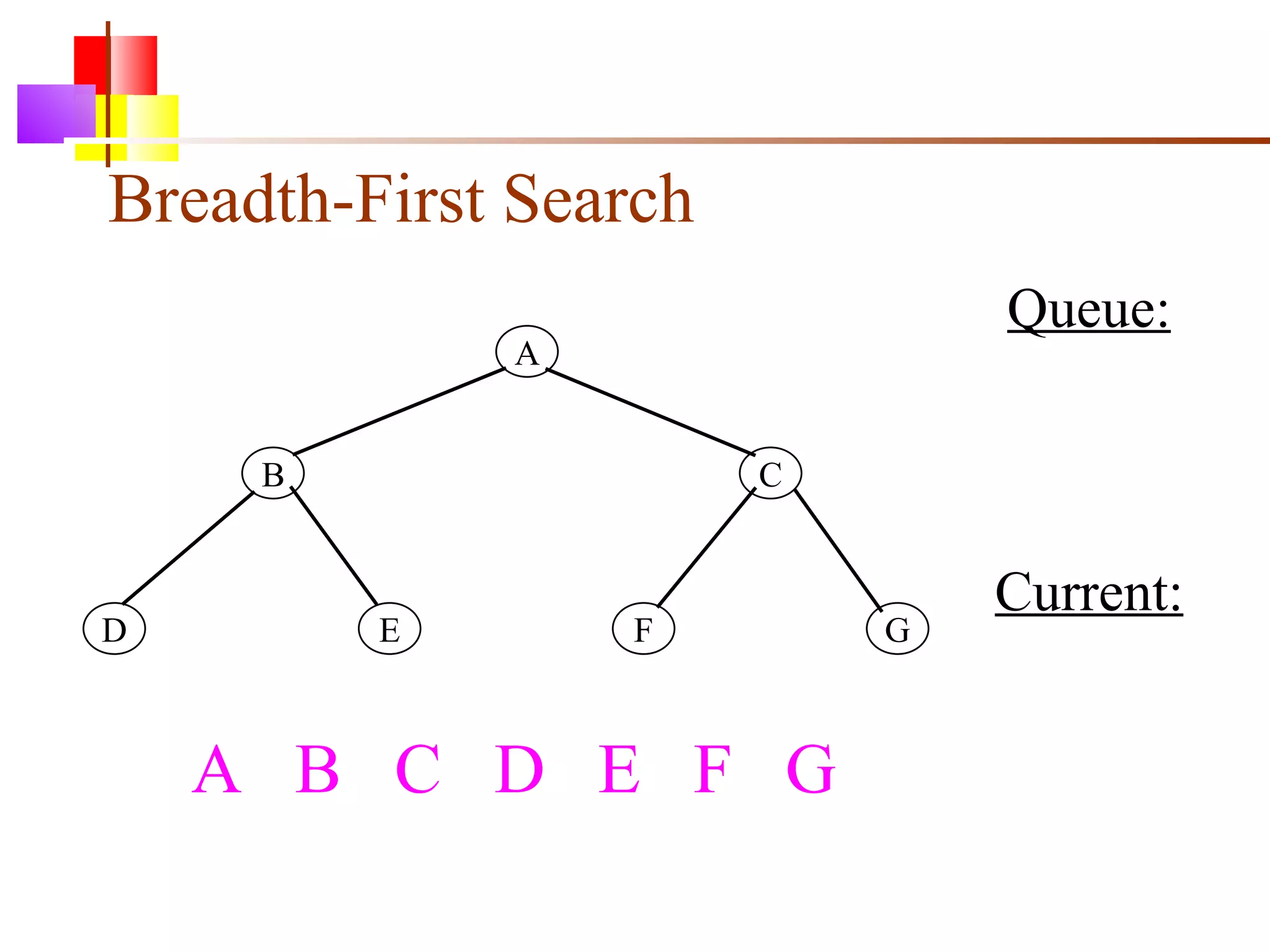
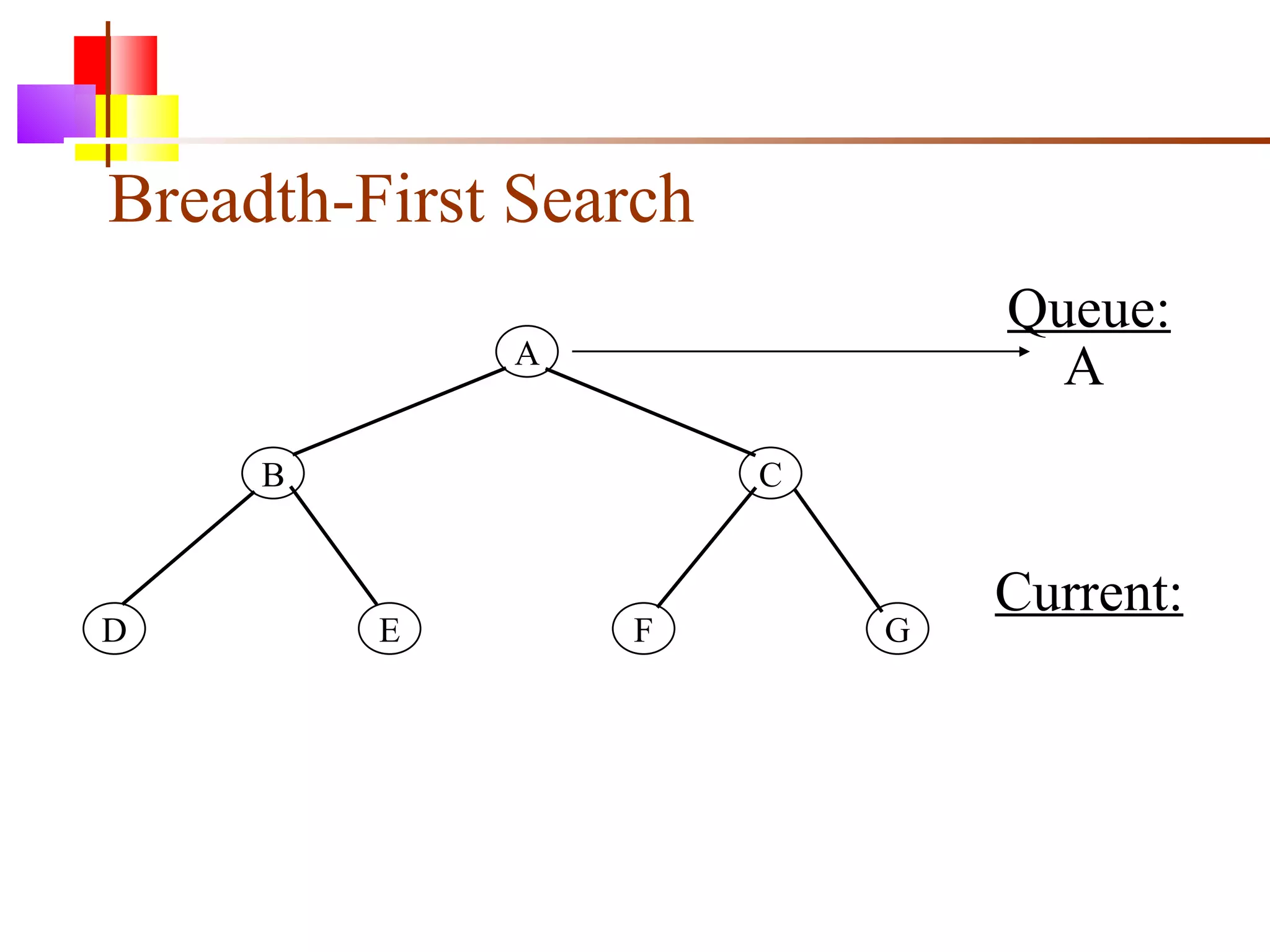
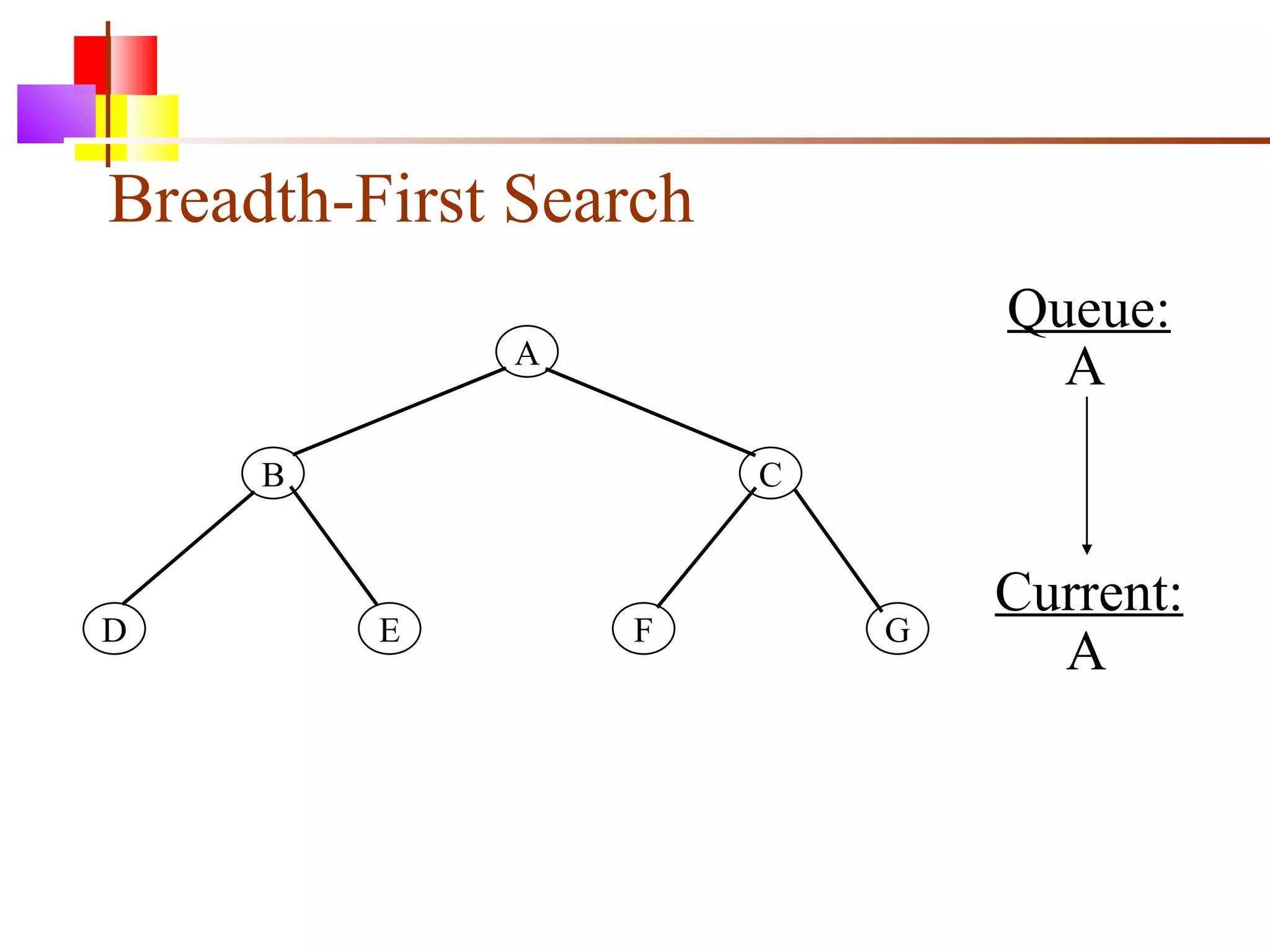
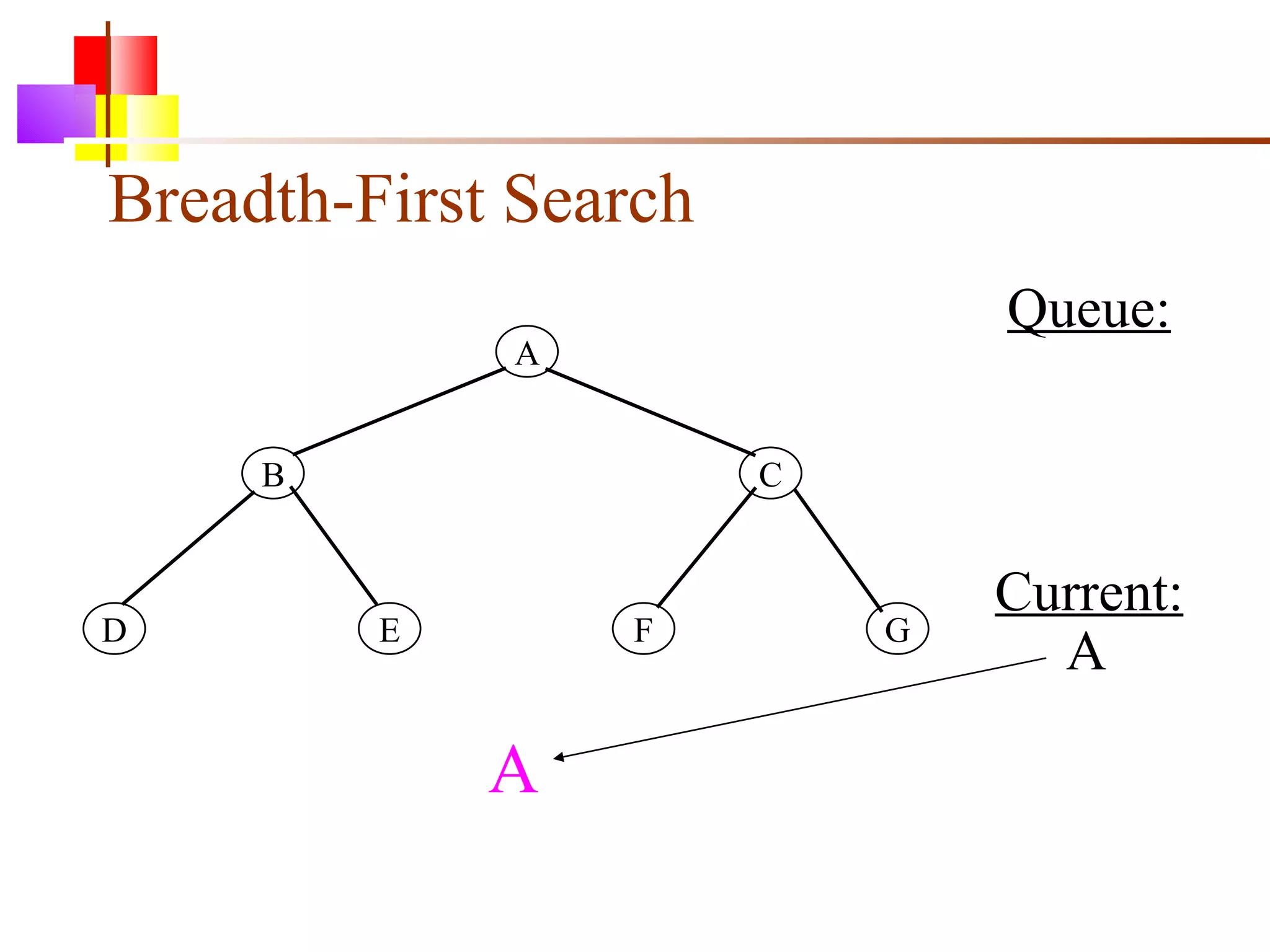
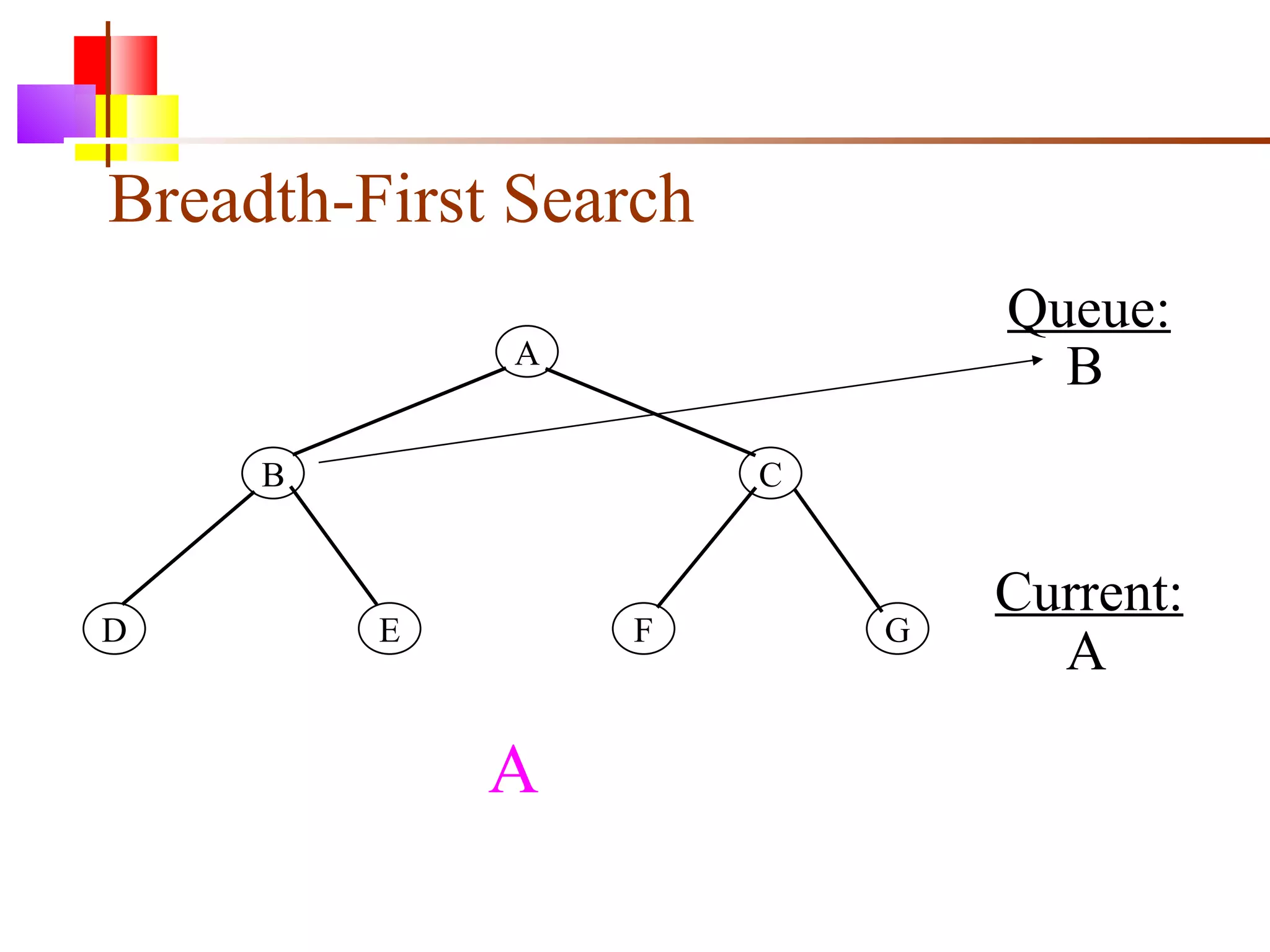
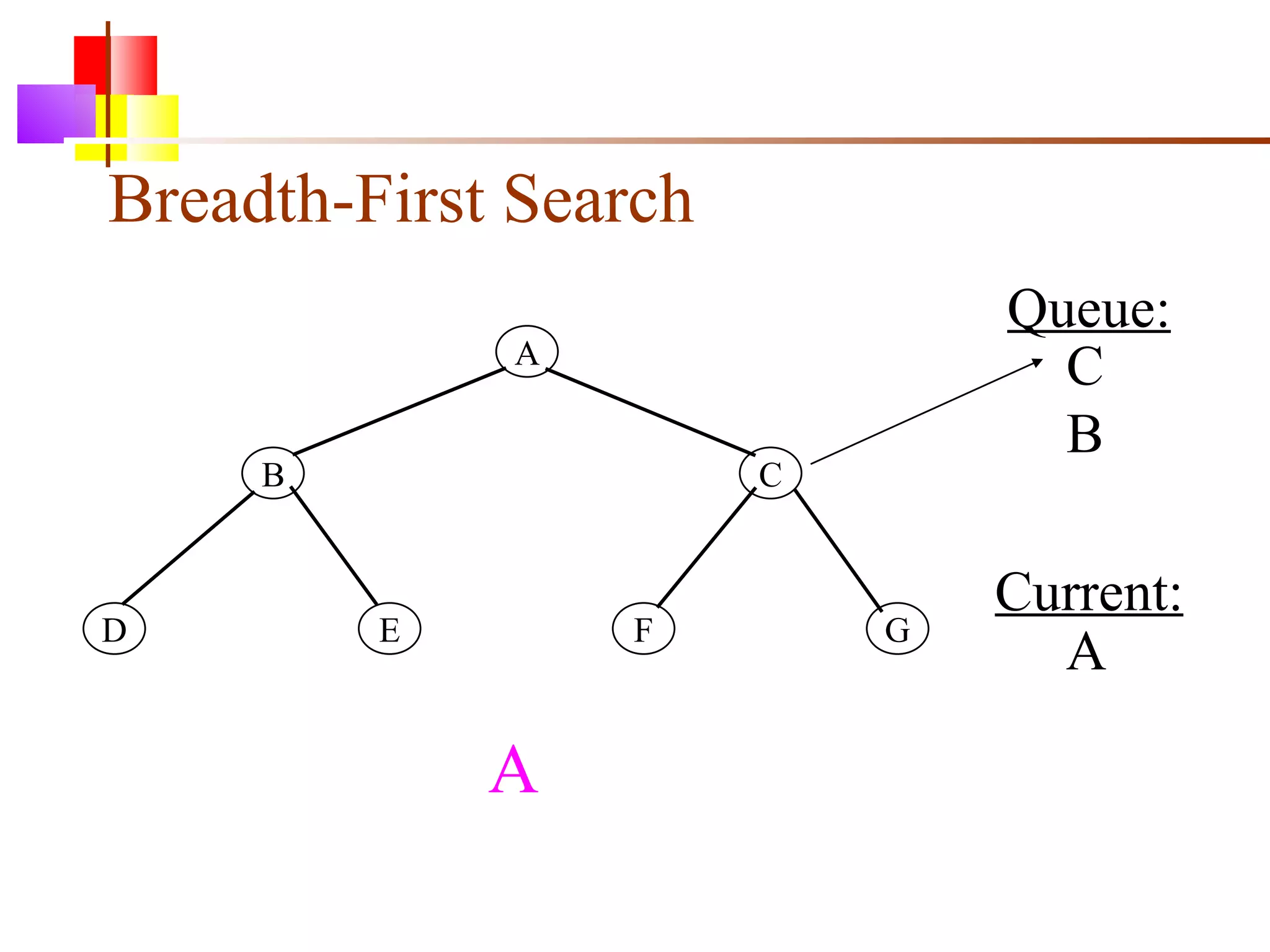
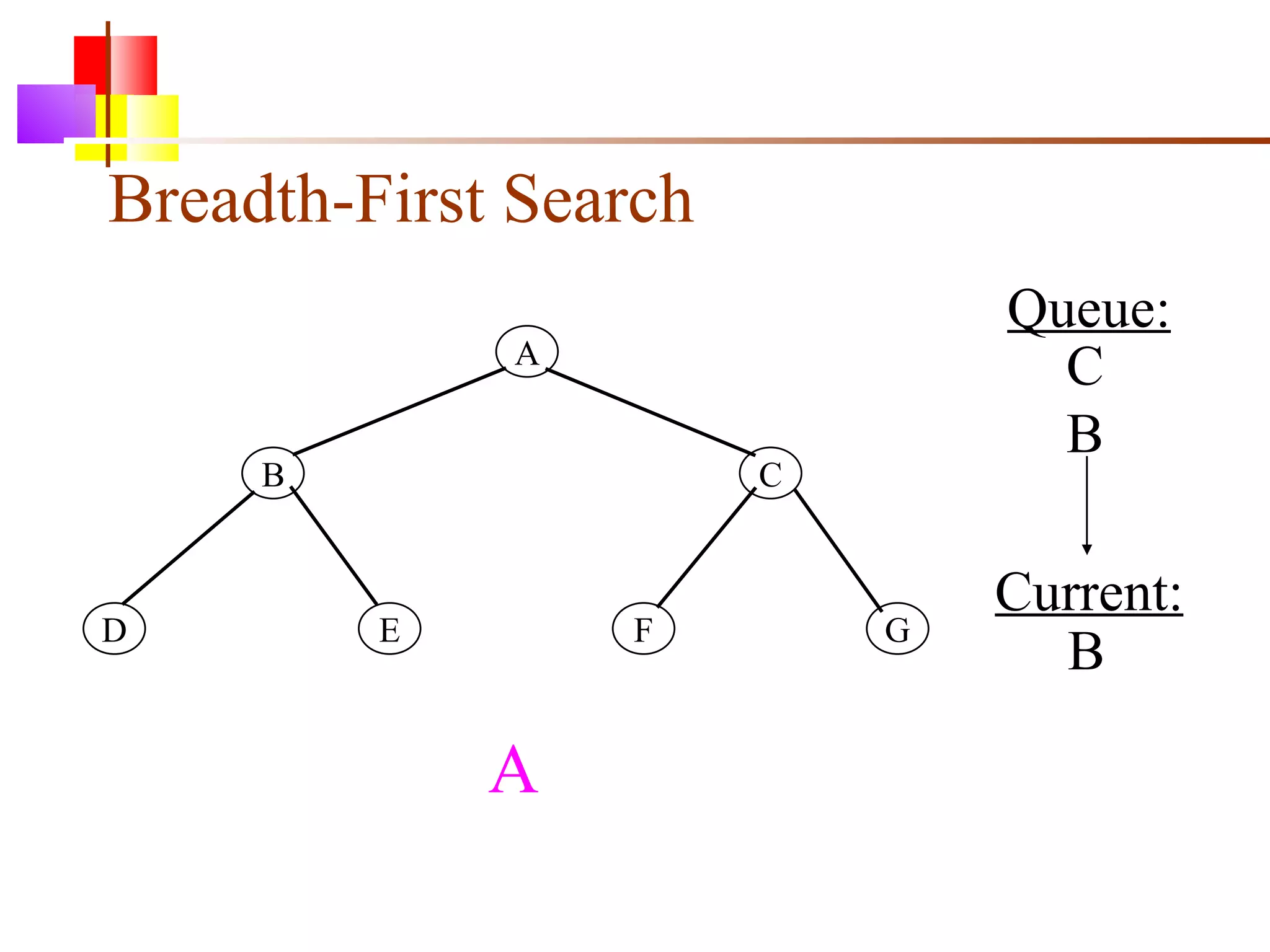
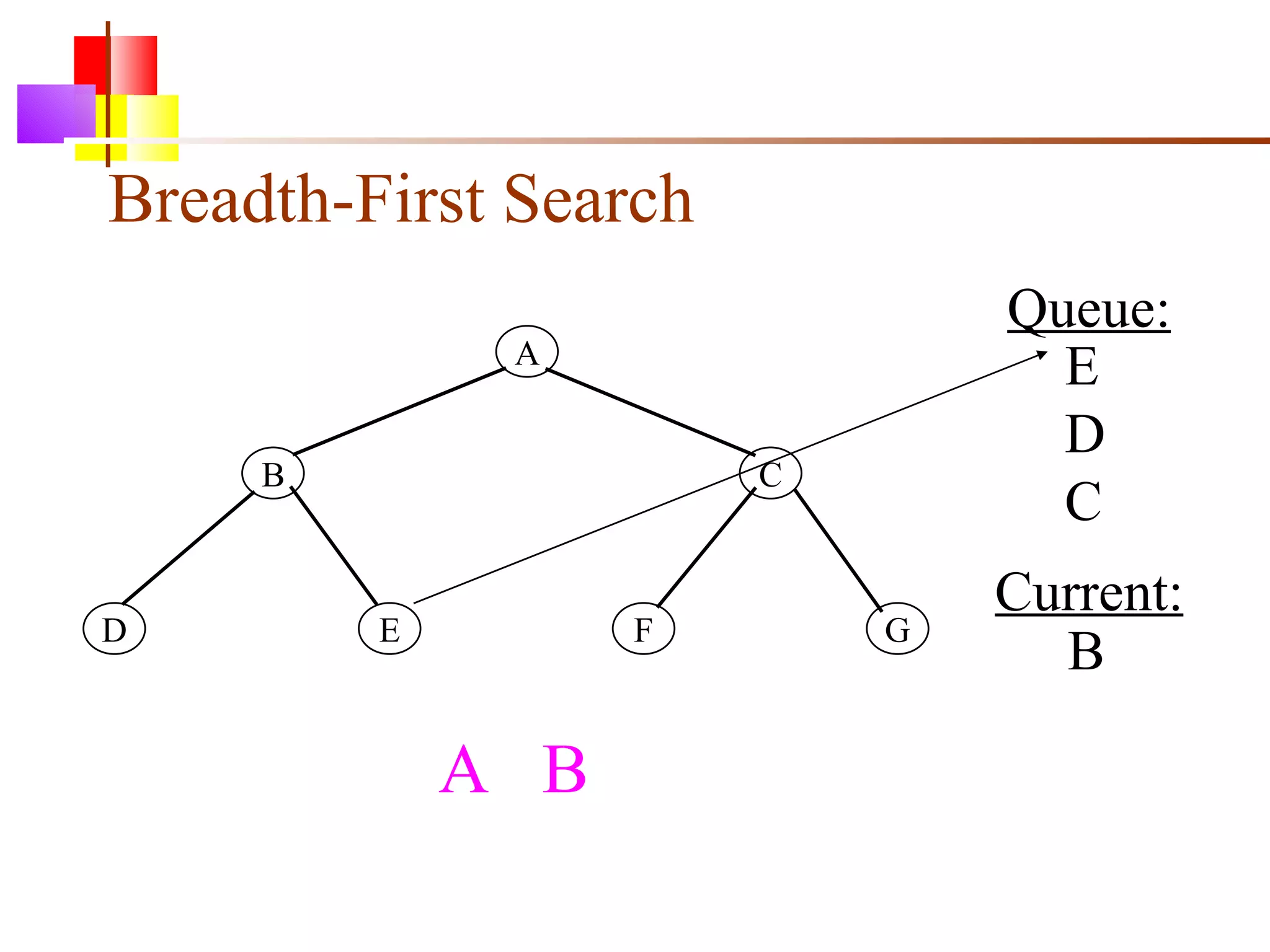
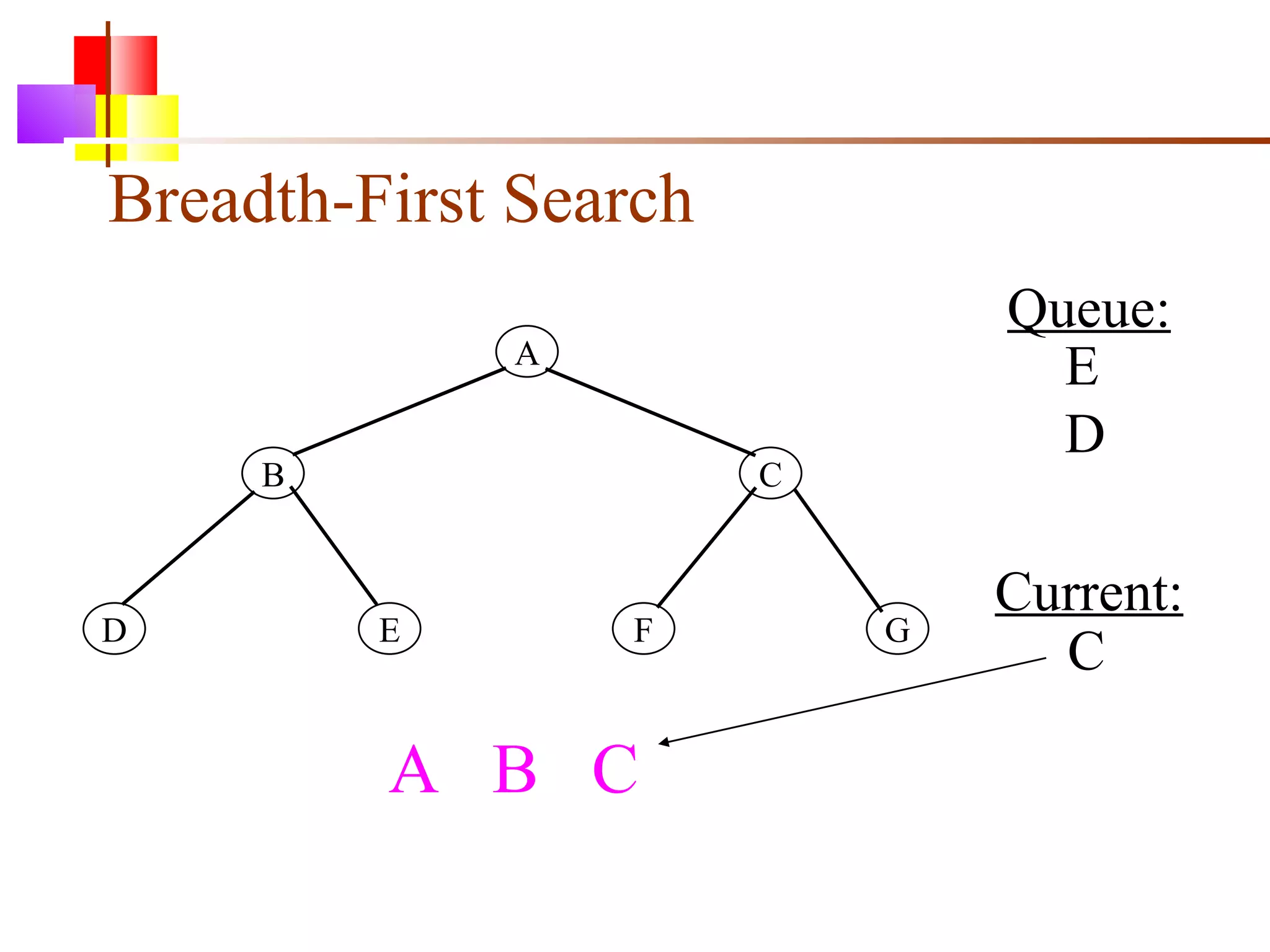
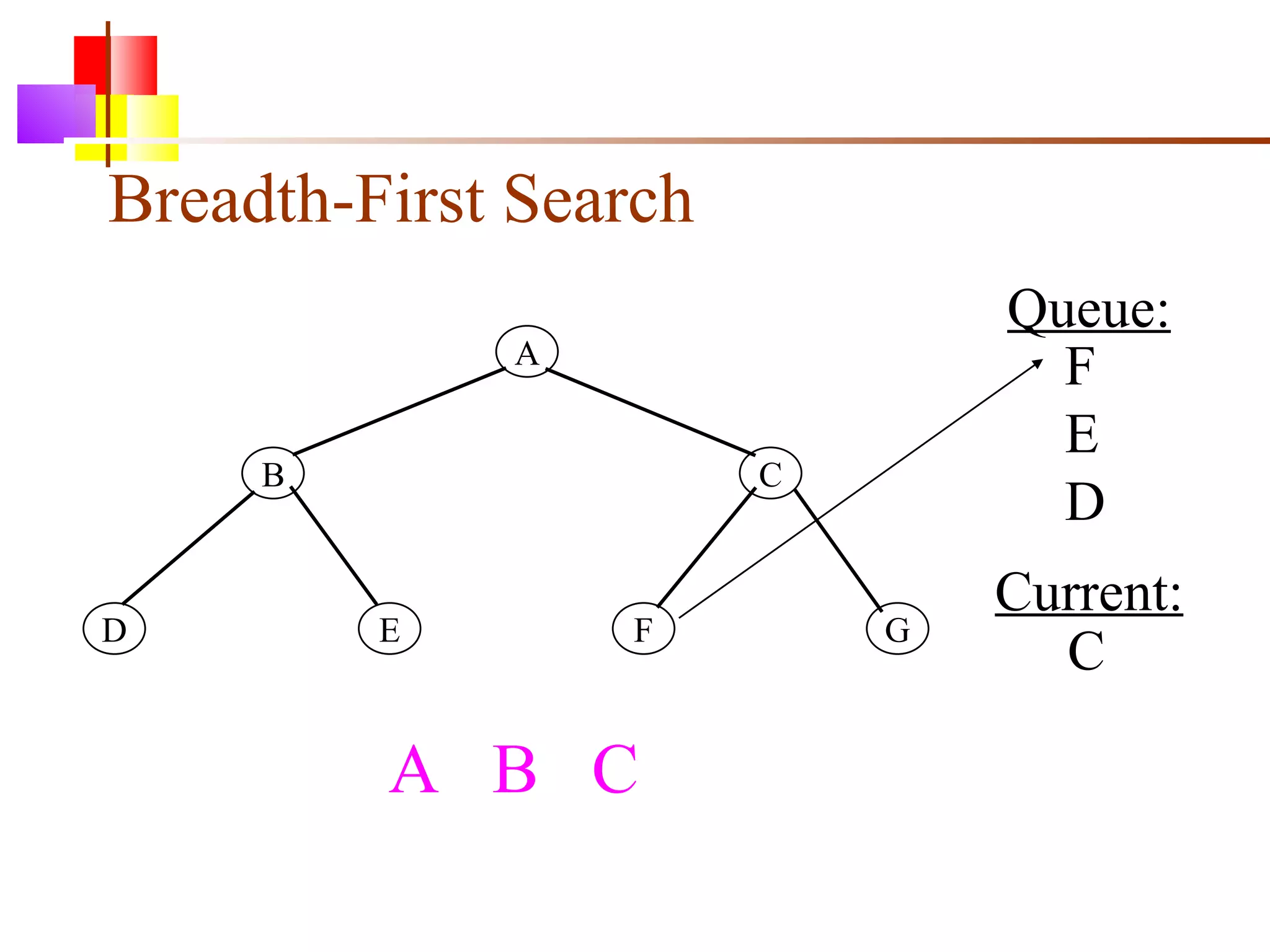
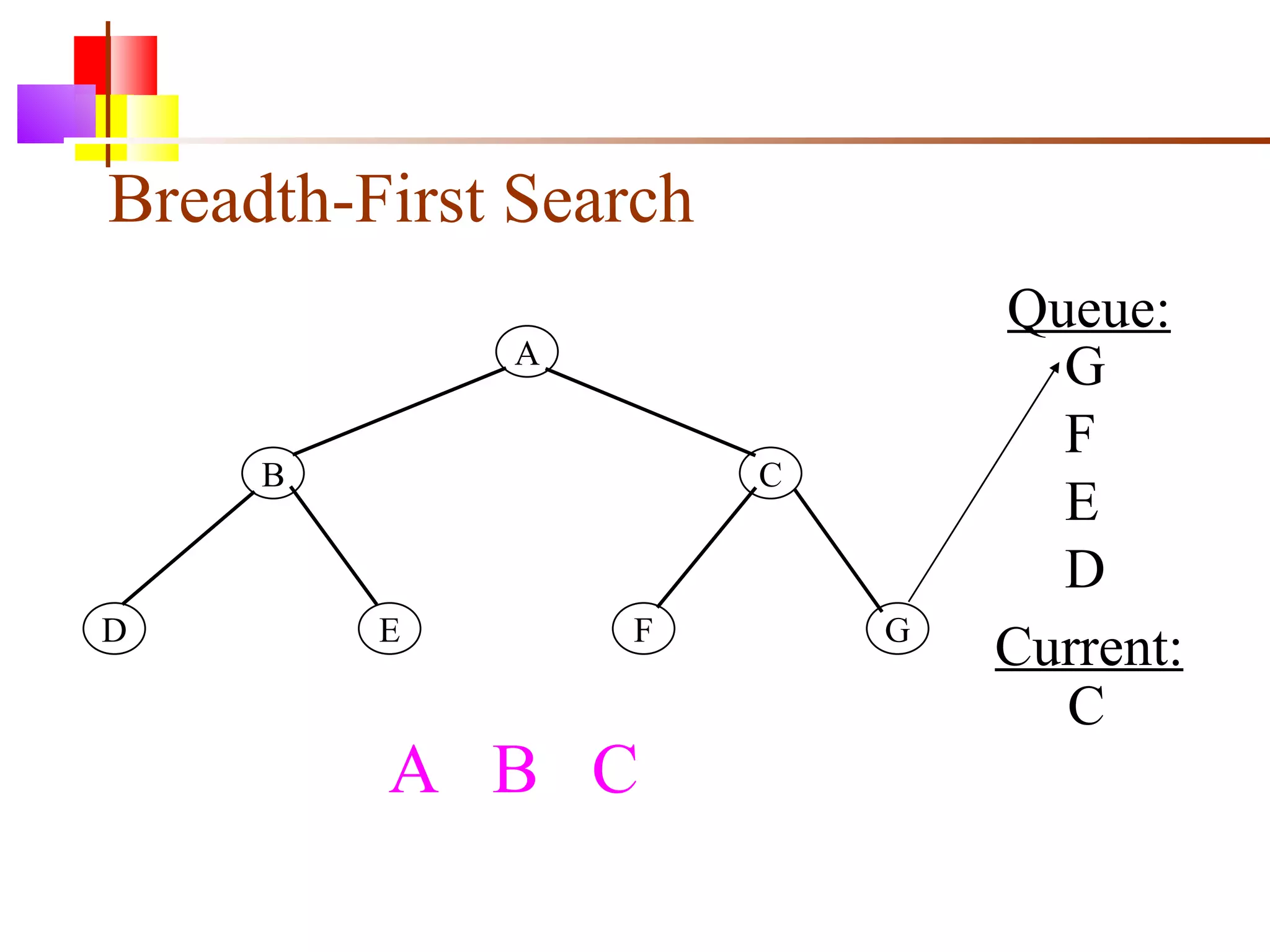
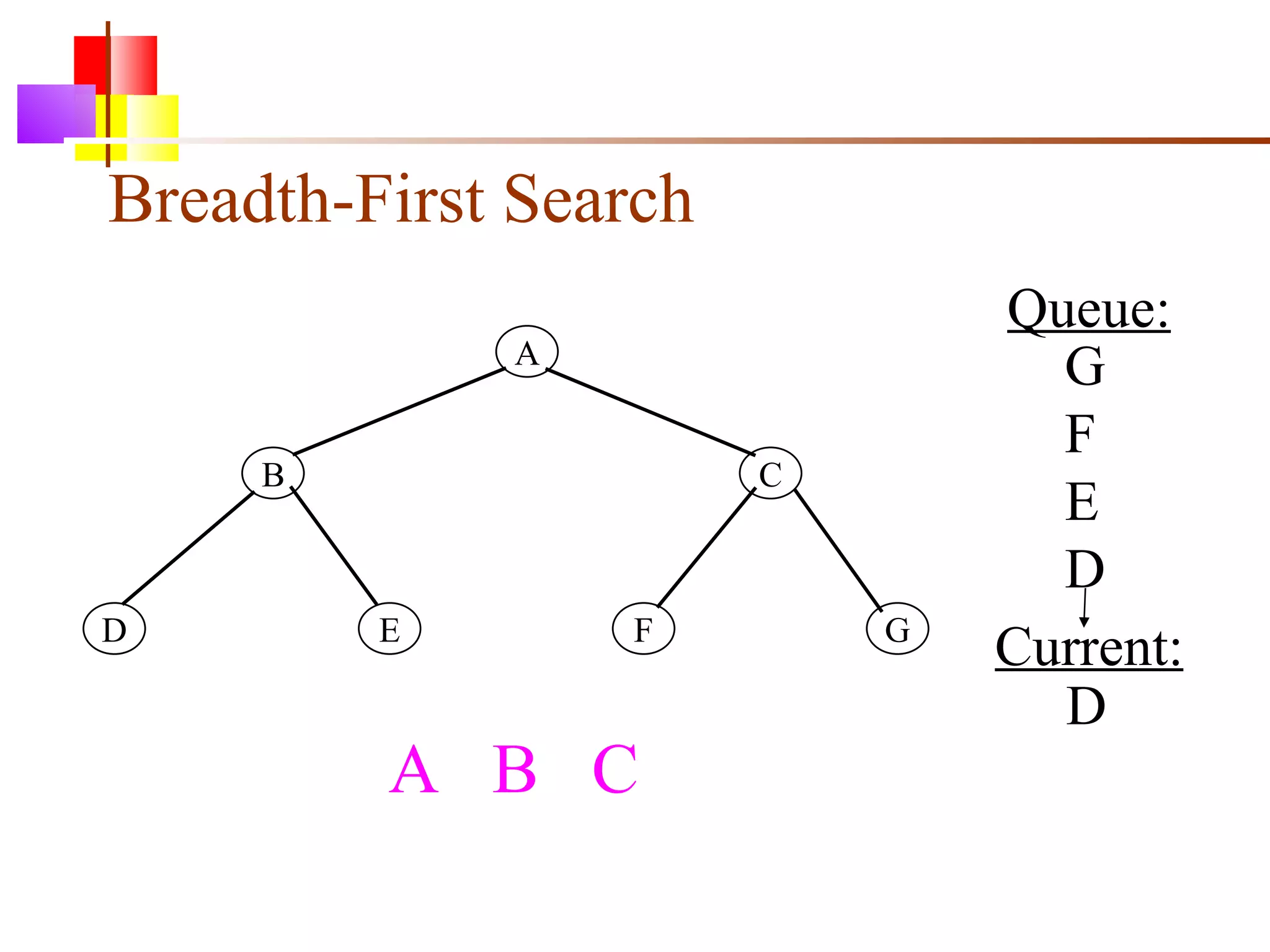
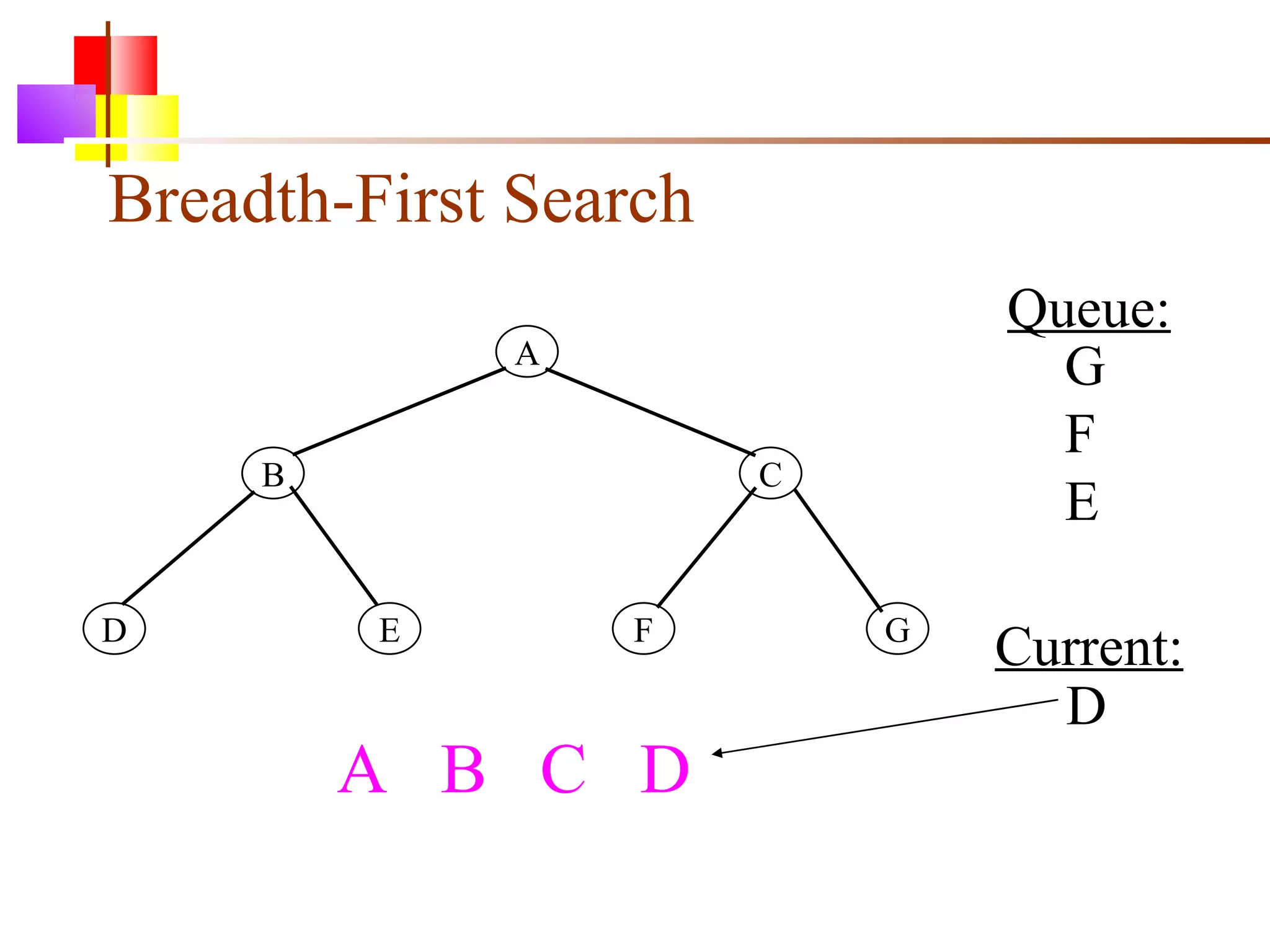
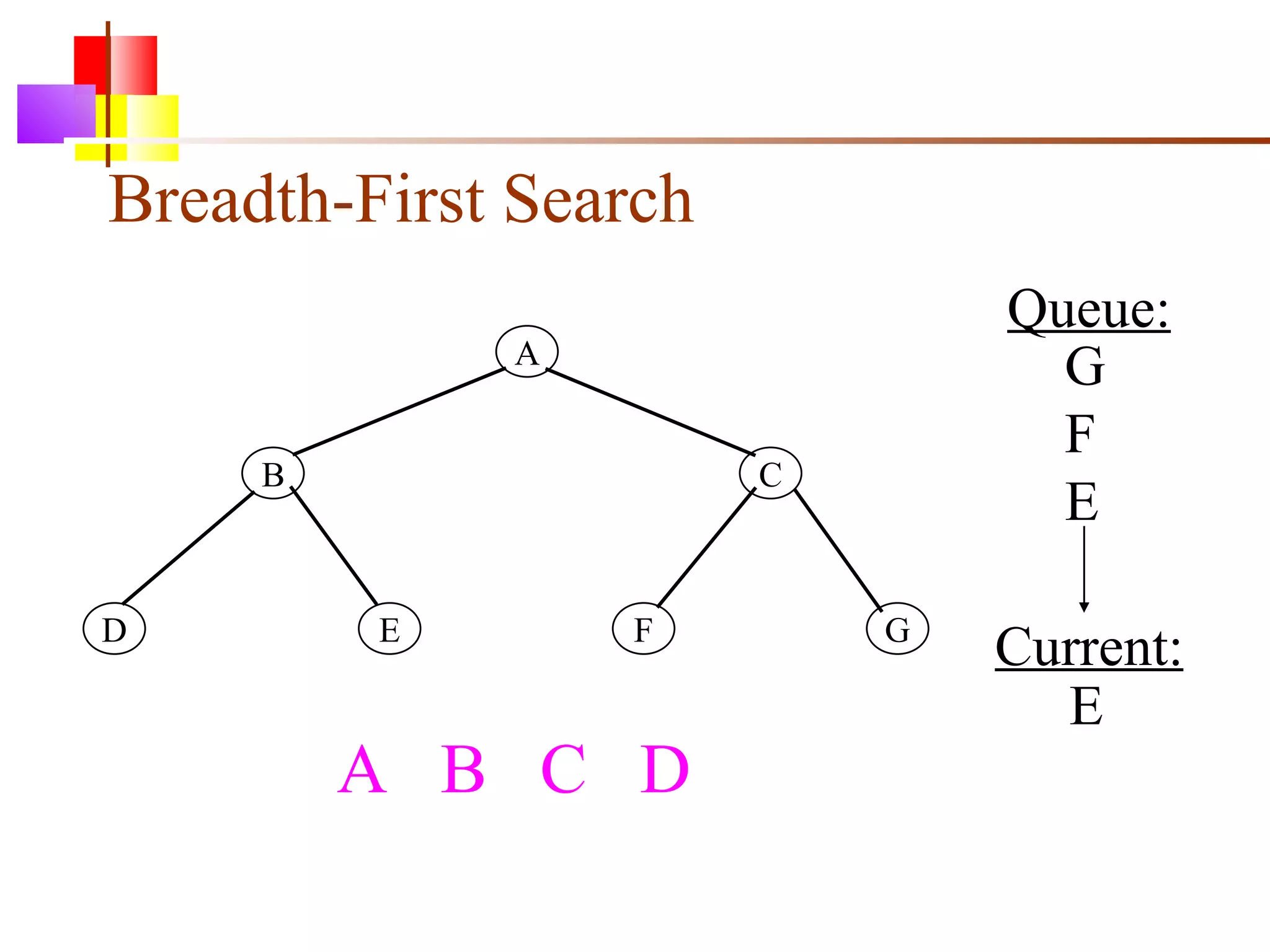
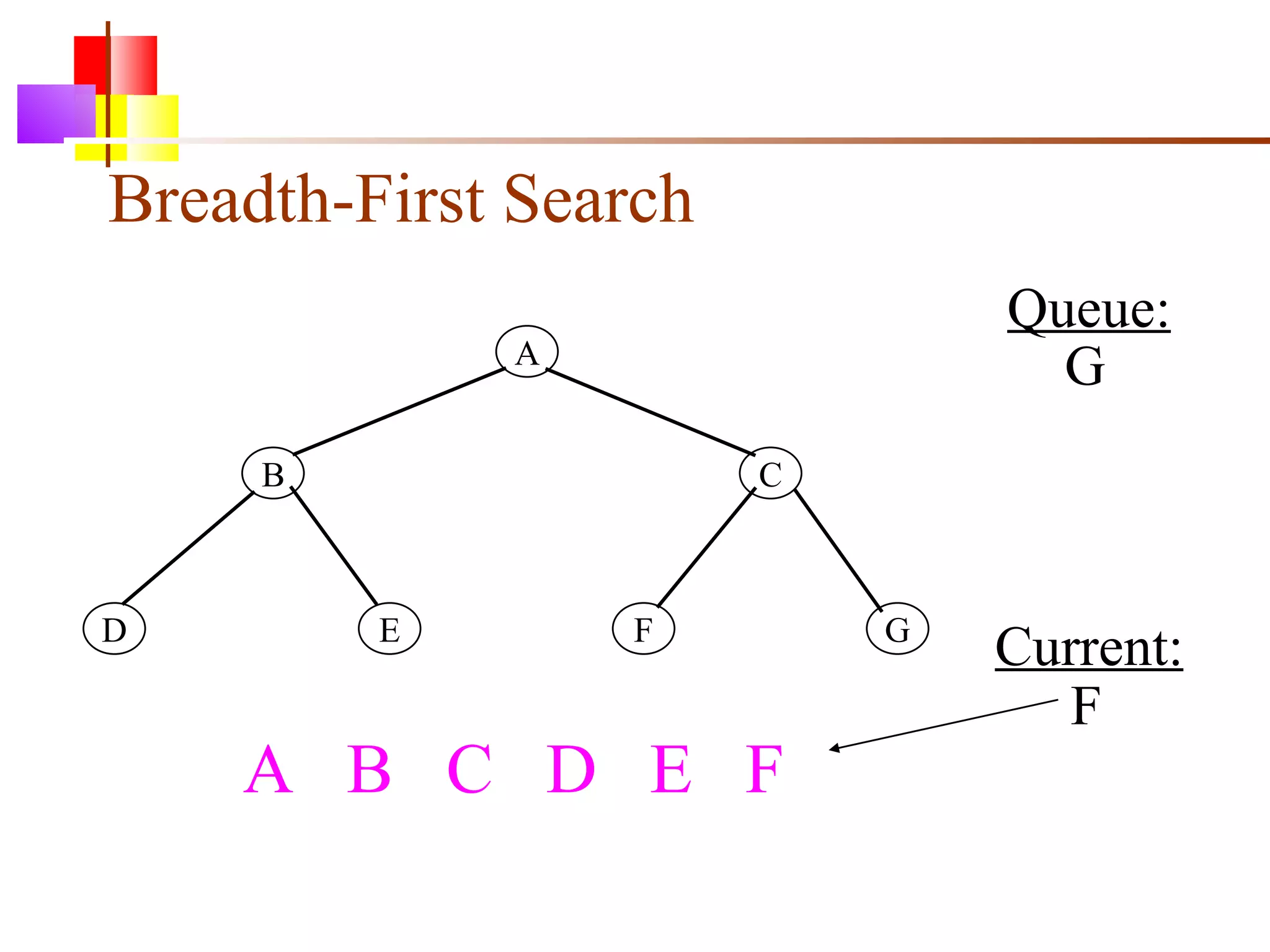
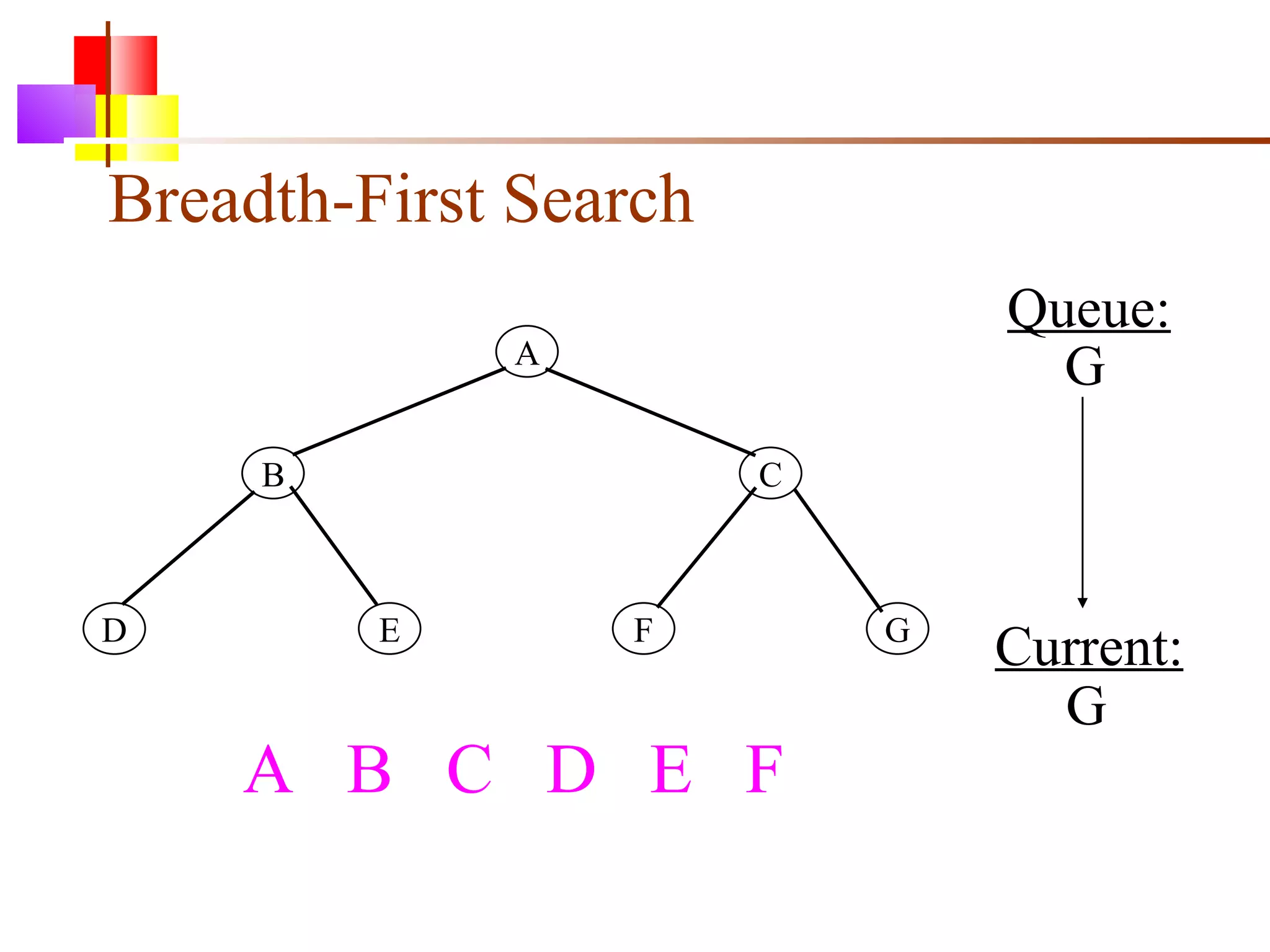
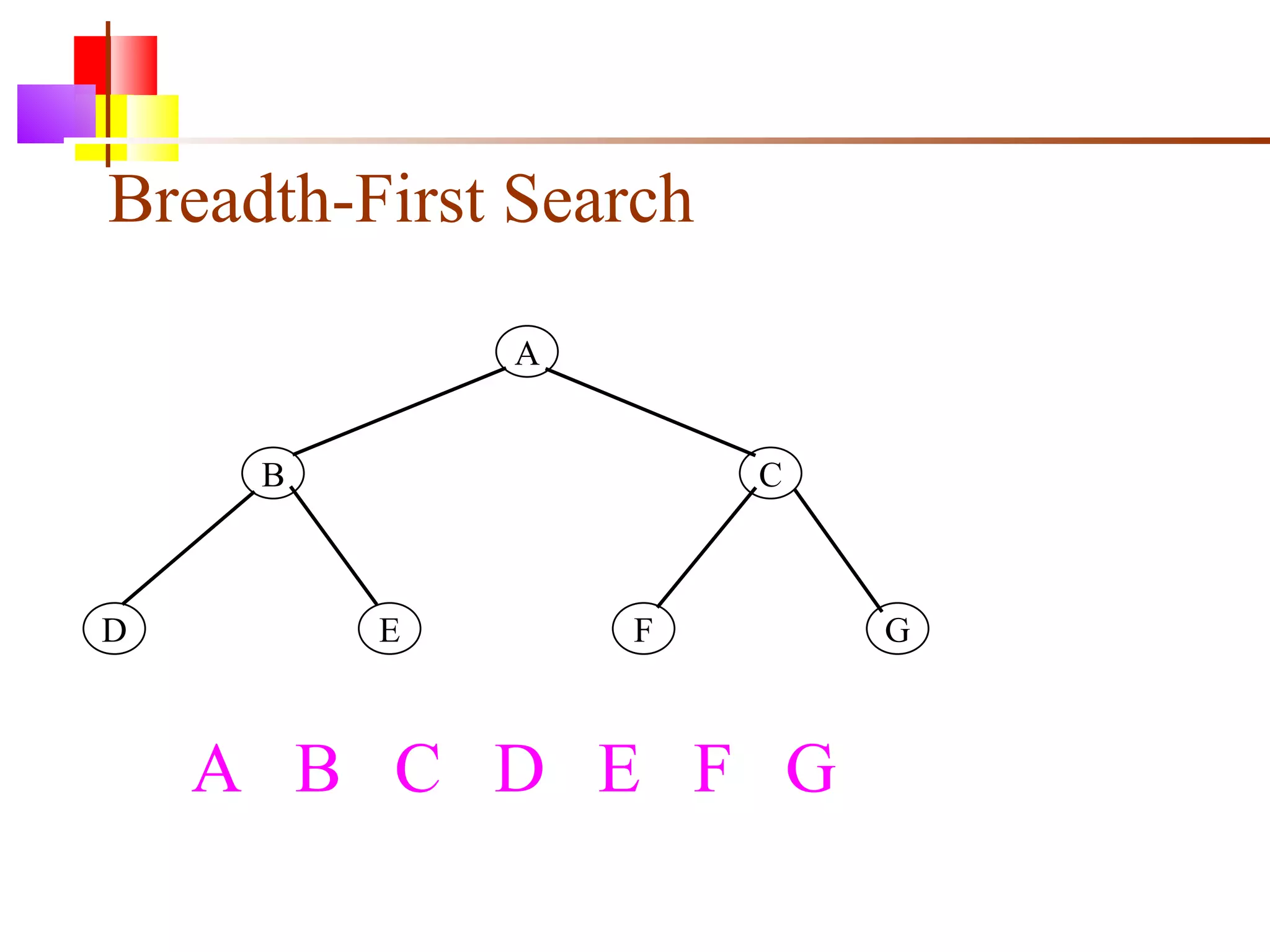
The document discusses binary trees and various operations on them. It defines what a binary tree is composed of (nodes with values and pointers to left and right children). It describes tree traversals like preorder, inorder and postorder that output the nodes in different orders. It explains two common search strategies - depth-first search (DFS) and breadth-first search (BFS) - and provides examples of how they traverse a sample tree. It also briefly discusses operations like finding the minimum/maximum element, inserting a new element, and deleting an existing element from the binary search tree.