Downloaded 551 times
Uploaded byAjay Kumar Sharma
Pipe sizing
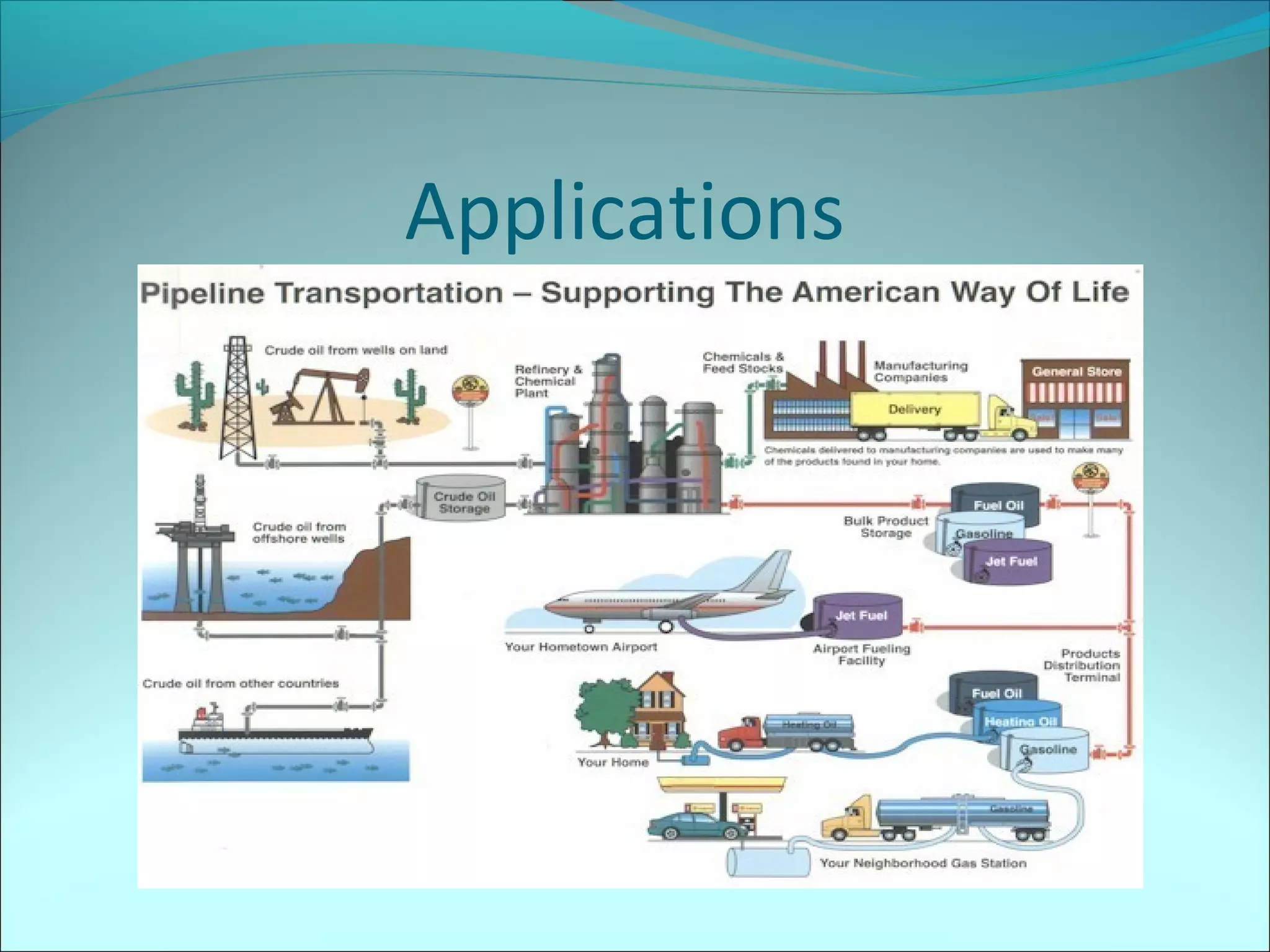
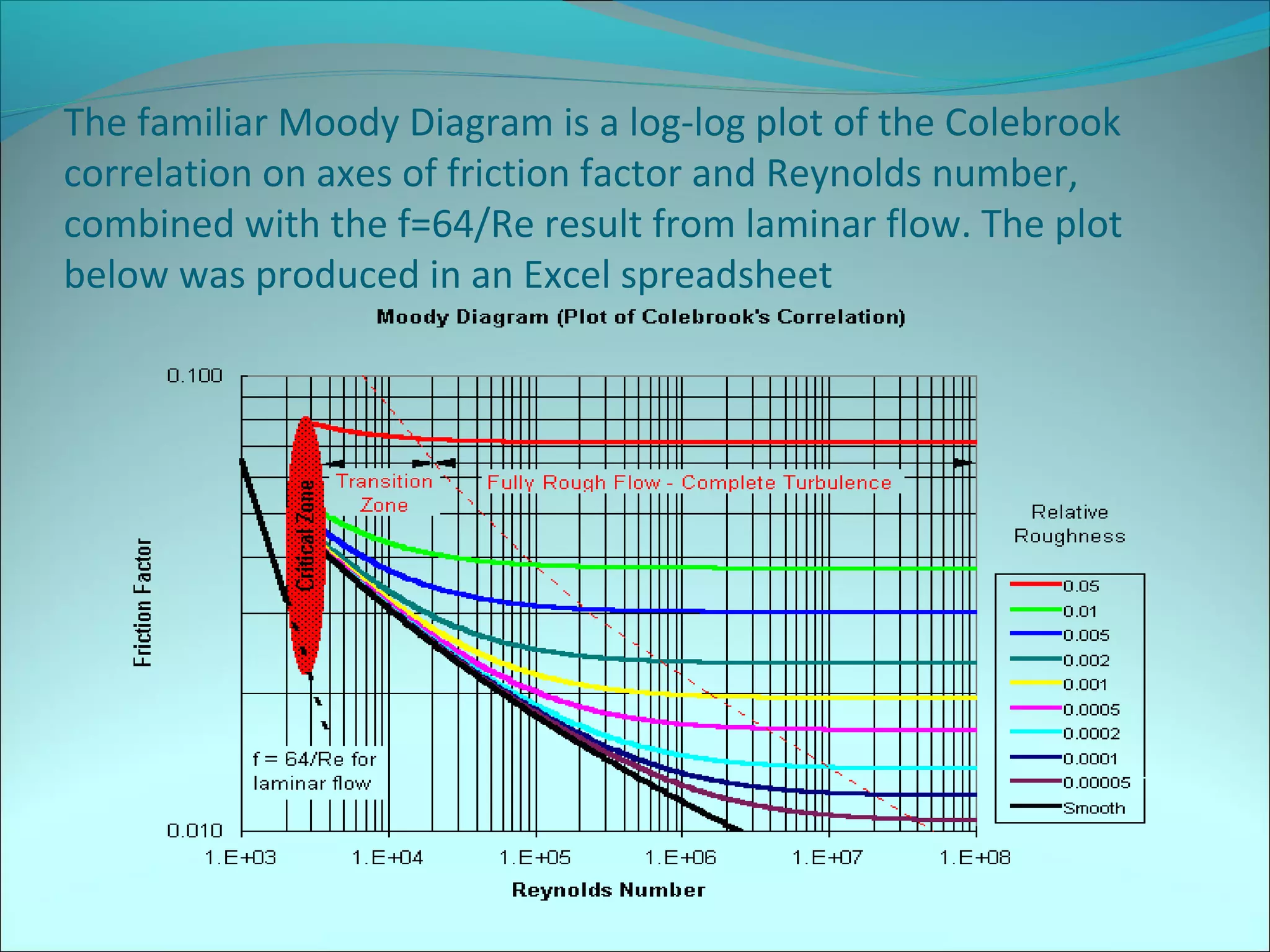
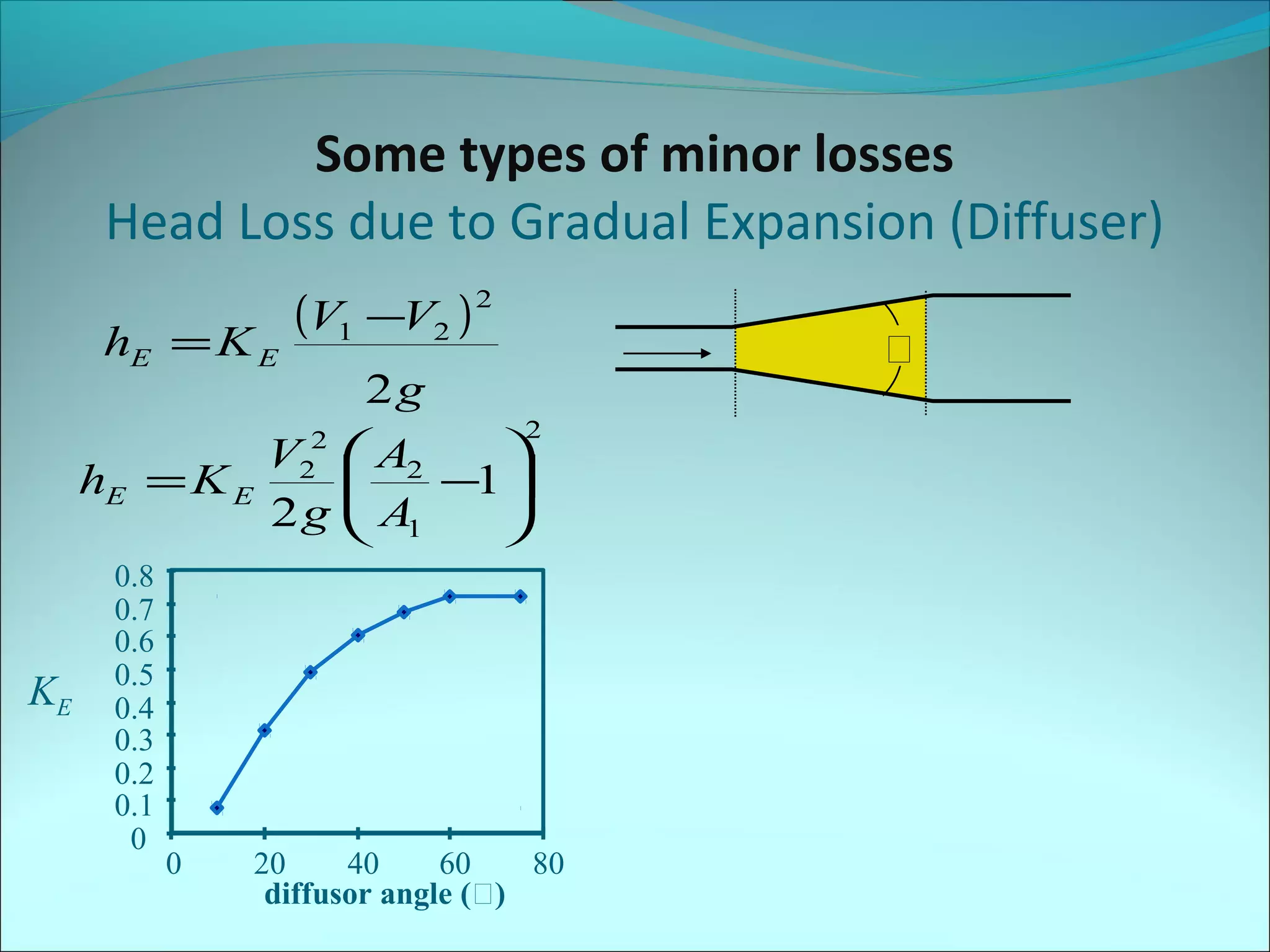
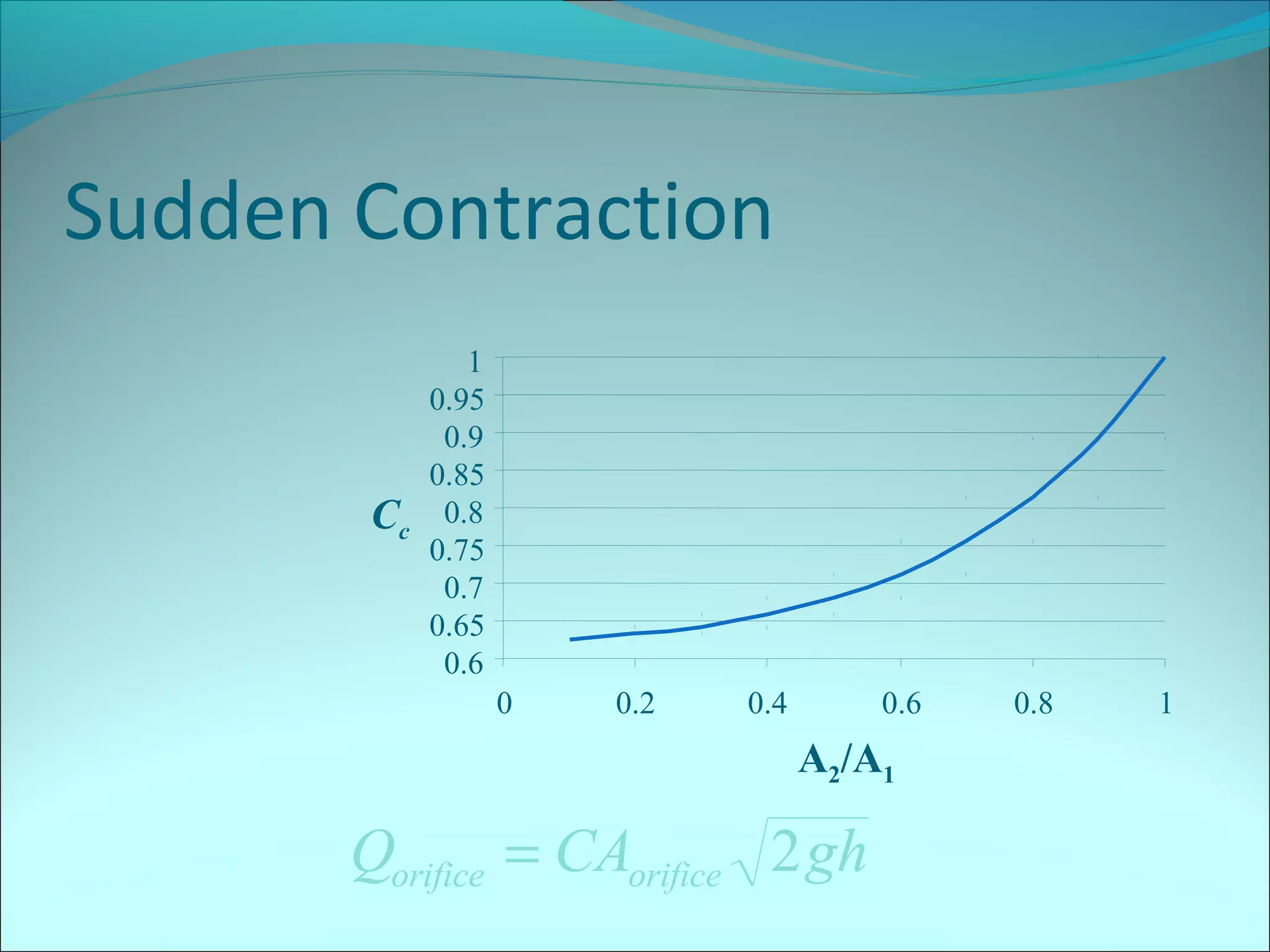
This document provides information on calculating head losses in piping systems. It discusses the use of Bernoulli's equation to relate total head between two points in a piping system. It also covers friction losses using the Darcy-Weisbach equation and the Moody diagram, as well as "minor losses" from fittings, valves, etc. The document presents methods to calculate head loss or flow rate given the other, including iterative techniques. It concludes with an example problem calculating maximum flow between reservoirs considering major and minor losses.
More Related Content
Pipe sizing
- 1. Major & MinorLosses Under Supervision of: Prof. Dr. Mahmoud Fouad By students: Mahmoud Bakr 533 Mohammed Abdullah 511 Moaz Emad 619 Mohammed Nabil Abbas 525
- 2.
- 3. How big doesthe pipe have to be to carry 3 a flow of x m /s?
- 4. Bernoulli's Equation The basicapproach to all piping systems is to write the Bernoulli equation between two points, connected by a streamline, where the conditions are known. For example, between the surface of a reservoir and a pipe . outlet The total head at point 0 must match with the total head at point 1, adjusted for any increase in head due to pumps, losses due to pipe friction and so-called "minor losses" due to entries, exits, fittings, etc. Pump head developed is generally a function of the flow through the system
- 5.
- 6. Friction Losses inPipes Friction losses are a complex function of the system geometry, the fluid properties and the flow rate in the system. By observation, the head loss is roughly proportional to the square of the flow rate in most engineering flows (fully developed, turbulent pipe flow). This observation leads to the Darcy-Weisbach equation for head loss due to friction
- 9. For laminar flow,the head loss is proportional to velocity rather than velocity squared, thus the friction factor is inversely proportional to velocity
- 10. Turbulent flow For turbulentflow, Colebrook (1939) found an implicit correlation for the friction factor in round pipes. This correlation converges well in few iterations. Convergence can be optimized by slight under-relaxation.
- 11. The familiar MoodyDiagram is a log-log plot of the Colebrook correlation on axes of friction factor and Reynolds number, combined with the f=64/Re result from laminar flow. The plot below was produced in an Excel spreadsheet
- 12.
- 13. Pipe roughness pipe material glass,drawn brass, copper commercial steel or wrought iron asphalted cast iron galvanized iron cast iron concrete rivet steel corrugated metal PVC pipe roughness ε (mm) 0.0015 0.045 ε 0.12 d Must be 0.15 dimensionless! 0.26 0.18-0.6 0.9-9.0 45 0.12
- 14. Calculating Head Lossfor a Known Flow From Q and piping determine Reynolds Number, relative roughness and thus the friction factor. Substitute into the Darcy-Weisbach equation to obtain head loss for the given flow. Substitute into the Bernoulli equation to find the necessary elevation or pump head
- 15. Calculating Flow fora Known Head Obtain the allowable head loss from the Bernoulli equation, then start by guessing a friction factor. (0.02 is a good guess if you have nothing better.) Calculate the velocity from the Darcy-Weisbach equation. From this velocity and the piping characteristics, calculate Reynolds Number, relative roughness and thus . friction factor Repeat the calculation with the new friction factor until sufficient convergence is obtained. Q = VA
- 16. "Minor Losses" Although theyoften account for a major portion of the head loss, especially in process piping, the additional losses due to entries and exits, fittings and valves are traditionally referred to as minor losses. These losses represent additional energy dissipation in the flow, usually caused by secondary flows induced by curvature or recirculation. The minor losses are any head loss present in addition to the head loss for the same . length of straight pipe Like pipe friction, these losses are roughly proportional to the square of the flow rate. Defining K, the loss coefficient, by
- 17. . K isthe sum of all of the loss coefficients in the length of pipe, each contributing to the overall head loss Although K appears to be a constant coefficient, it varies with different flow conditions : Factors affecting the value of K include .,the exact geometry of the component .the flow Reynolds number , etc
- 18. Some types ofminor losses Head Loss due to Gradual Expansion (Diffuser) (V1 −V2 ) 2 hE = K E 2g 2 2 V A hE = K E 2 2 −1 2 g A1 KE 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 20 40 60 80 diffusor angle ()
- 19. Sudden Contraction 2 1 V2 hc= −1 2 C 2g c V2 V1 flow separation losses are reduced with a gradual contraction = Ac C c A2
- 20.
- 21. Entrance Losses Losses canbe reduced by accelerating the flow gradually and eliminating the he = K e K e ≈1.0 K e ≈ 0 .5 vena contracta K e ≈ 0.04 V2 2g
- 22. Head Loss inBendspressure High Head loss is a function of the ratio of the bend radius to the pipe diameter (R/D) Velocity distribution returns to normal several pipe diameters downstream Possible separation from wall R D Low pressure hb = K b Kb varies from 0.6 - 0.9 V2 2g
- 23. Head Loss inValves Function of valve type and valve position The complex flow path through valves can result in high head loss (of course, one of the purposes of a valve is to create head loss when it is not fully open) hv = K v V2 2g
- 24. To calculate lossesin piping systems with both pipe friction and minor losses use
- 25. Solution Techniques Neglect minorlosses Equivalent pipe lengths Iterative Techniques Simultaneous Equations Pipe Network Software
- 26. Iterative Techniques forD and Q (given total head loss) Assume all head loss is major head loss. Calculate D or Q using Swamee-Jain equations Calculate minor losses Find new major losses by subtracting minor losses from total head loss
- 27. Solution Technique: HeadLoss Can be solved directly hminor = K Re = V 2 hminor = K 2g 4Q π ν D f = 8Q 2 gπ 2 D 4 0.25 2 ε 5.74 + log 3.7 D Re 0.9 hl = ∑ f +∑ minor h h hf = f 8 LQ 2 gπ 2 D 5
- 28. Solution Technique: Discharge orPipe Diameter Iterative technique Set up simultaneous equations in Excel Re = 4Q π ν D hminor = K f = 0.25 2 ε 5.74 log + 0 .9 3.7 D Re 8Q 2 gπ 2 D 4 hl = ∑ f +∑ minor h h hf = f 8 LQ 2 gπ 2 D 5 Use goal seek or Solver to find discharge that makes the calculated head loss equal the given head loss.
- 29. Example: Minor andMajor Losses Find the maximum dependable flow between the reservoirs for a water temperature range of 4ºC to 20ºC. Water 25 m elevation difference in reservoir water levels Reentrant pipes at reservoirs Standard elbows 2500 m of 8” PVC pipe 1500 m of 6” PVC pipe Sudden contraction Gate valve wide open
- 30. Directions Assume fully turbulent(rough pipe law) find f from Moody (or from von Karman) Find total head loss Solve for Q using symbols (must include minor losses) (no iteration required) Obtain values for minor losses from notes or text
- 31. Example (Continued) What arethe Reynolds number in the two pipes? Where are we on the Moody Diagram? What value of K would the valve have to produce to reduce the discharge by 50%? What is the effect of temperature? Why is the effect of temperature so small?
- 32. Example (Continued) Were theminor losses negligible? Accuracy of head loss calculations? What happens if the roughness increases by a factor of 10? If you needed to increase the flow by 30% what could you do? Suppose I changed 6” pipe, what is minimum diameter needed?