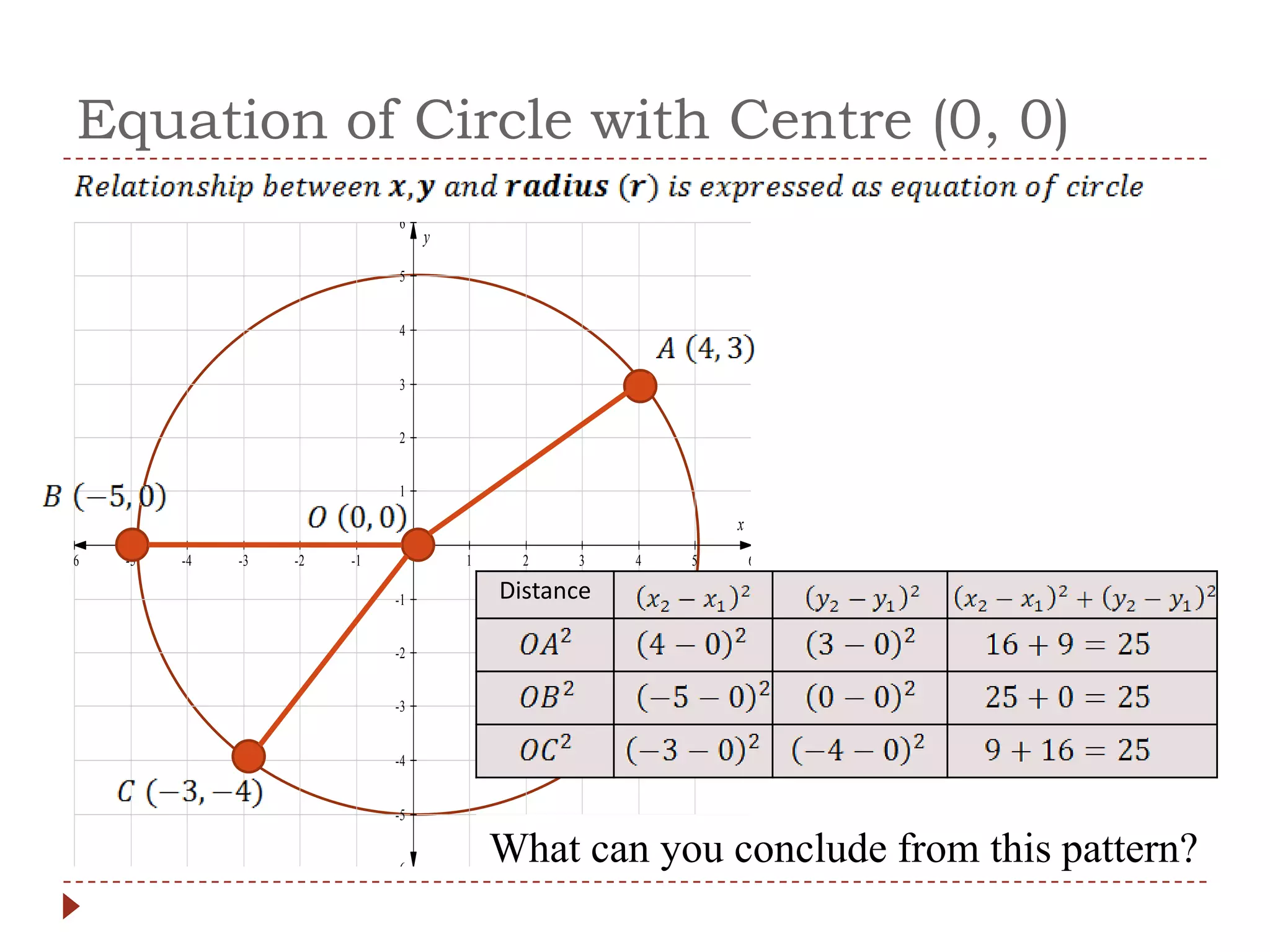
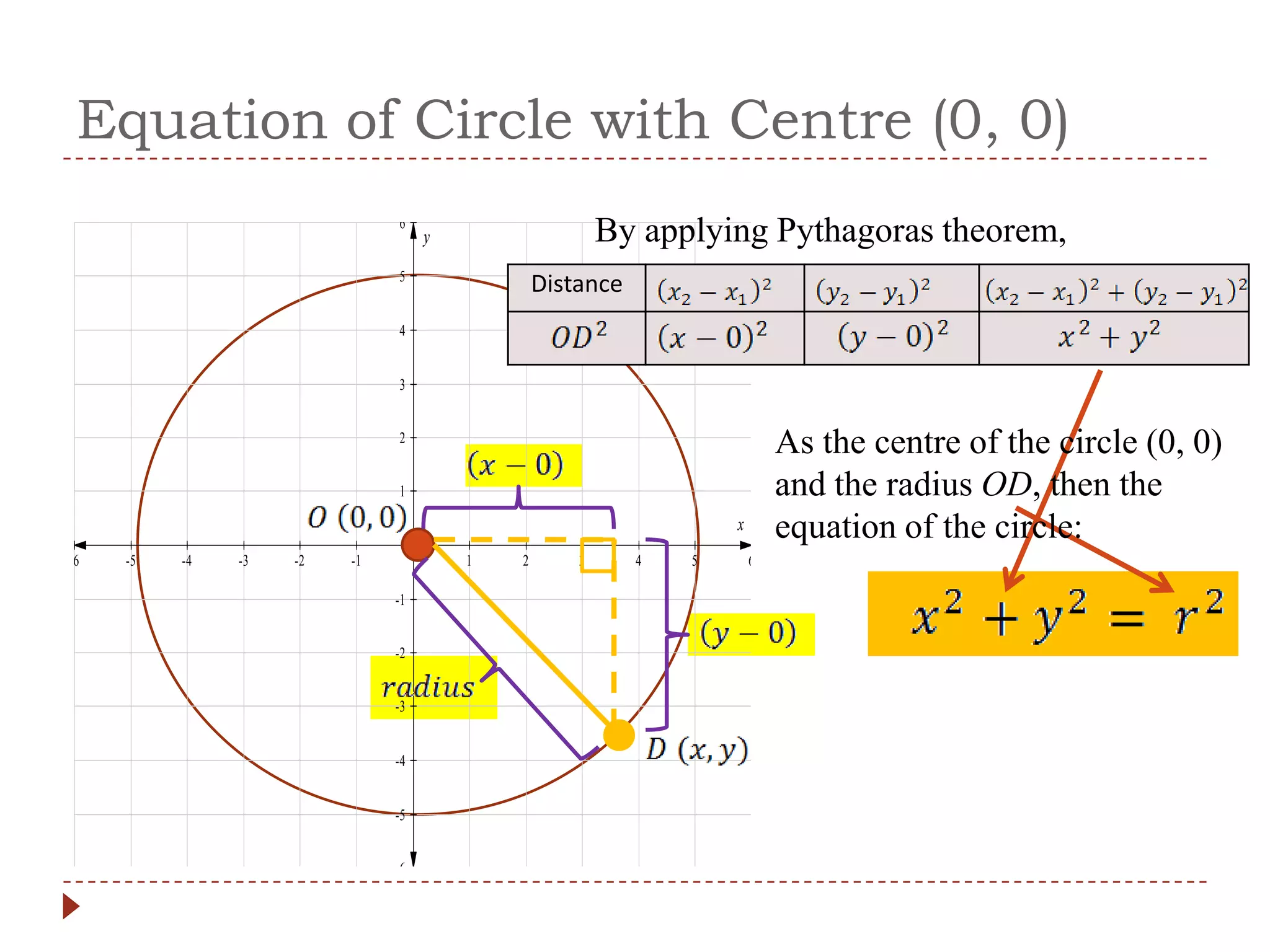
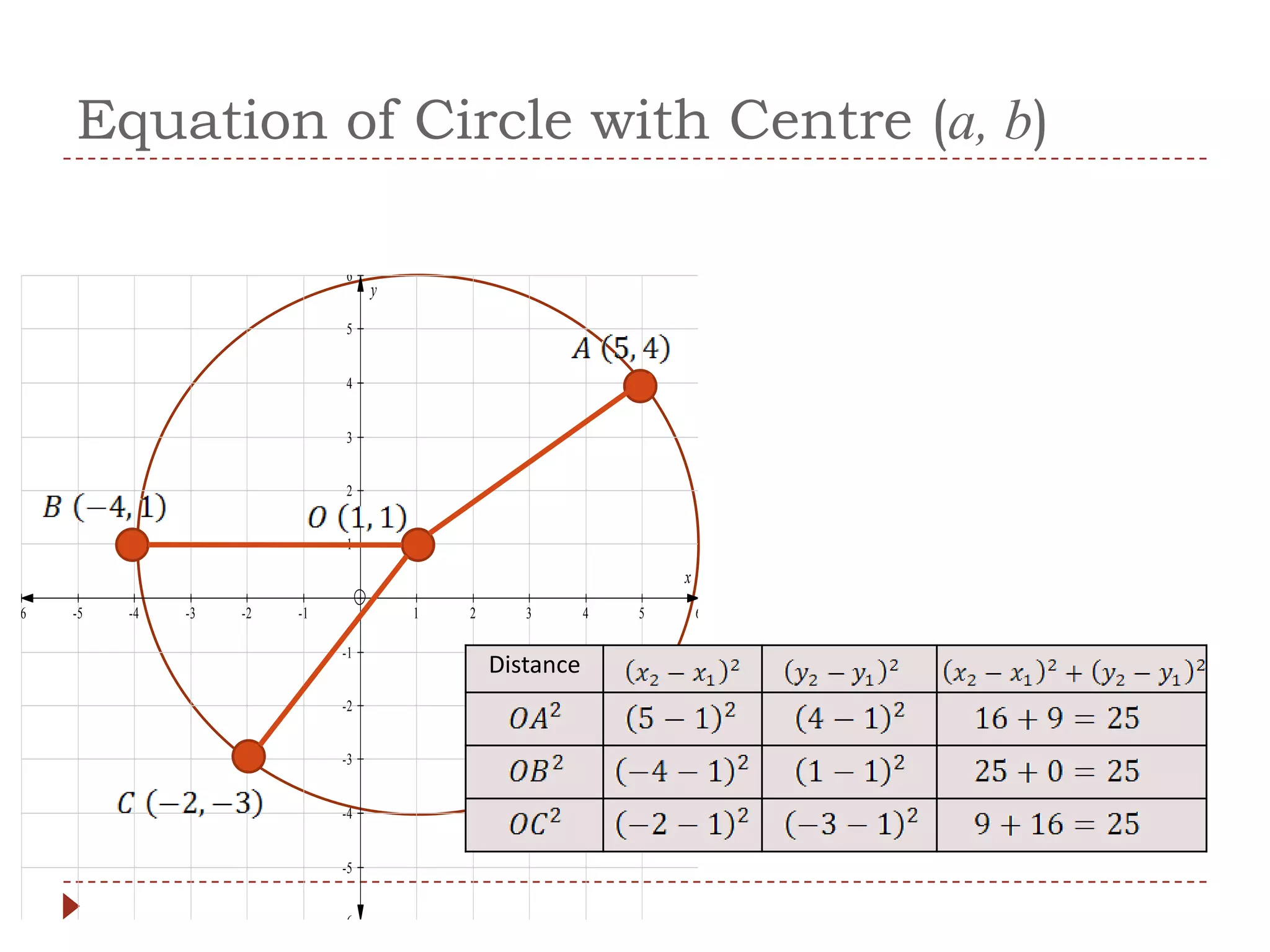
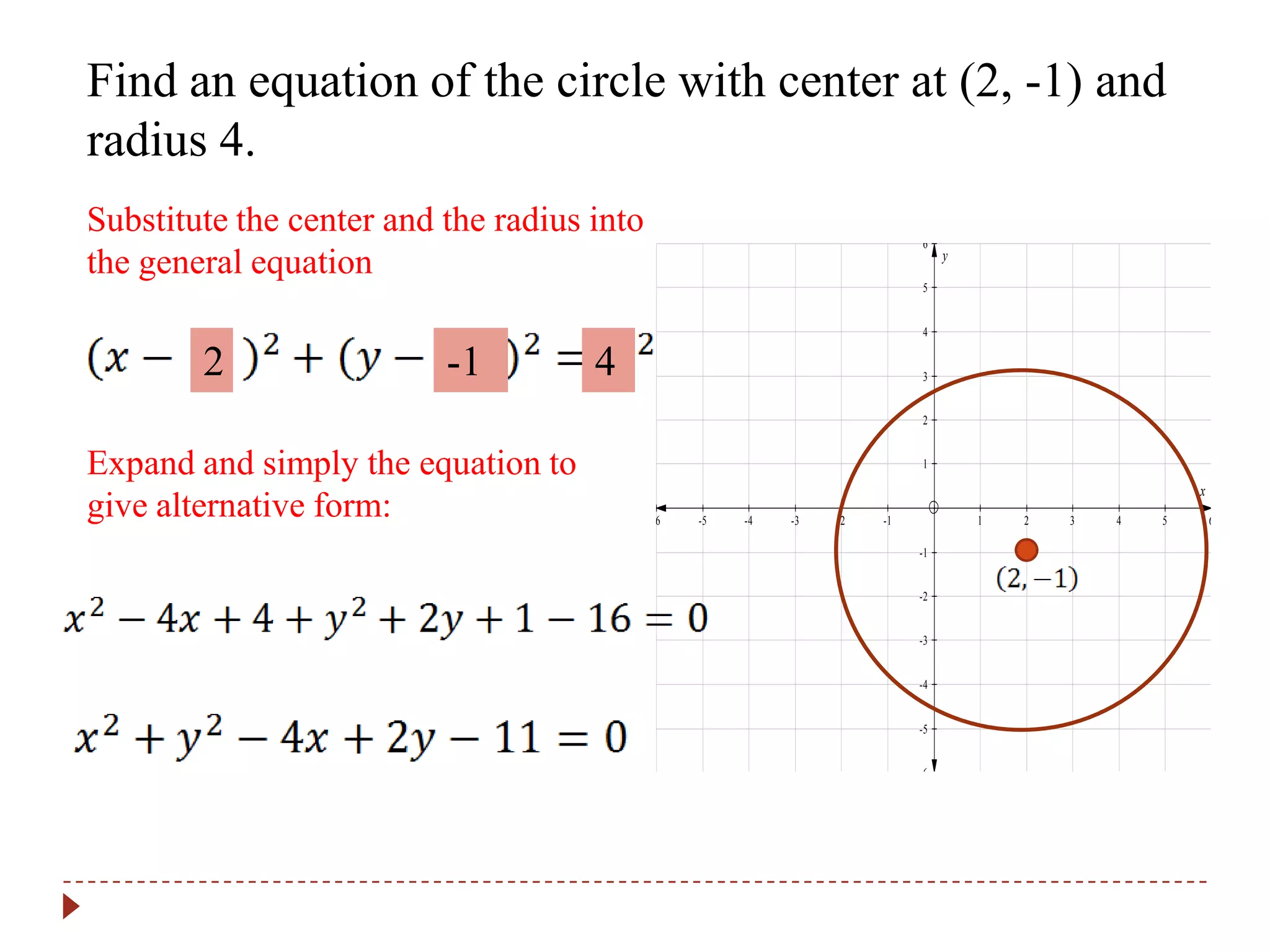
1) The document discusses the equation of a circle and how to derive it using the Pythagorean theorem and distance formula. 2) For a circle with center (0,0), the equation is x^2 + y^2 = r^2, where r is the radius. 3) More generally, for a circle with center (a,b), the equation is (x-a)^2 + (y-b)^2 = r^2, where (a,b) are the coordinates of the center and r is the radius.

1. Equation of Circle
Additional Mathematics

2. Distance between Two Points
5
y
4
3
2
1
x
-5 -4 -3 -2 -1 1 2 3 4 5
-1
-2
By Phytagoras Theorem:
-3
-4
-5

3. Equation of Circle with Centre (0, 0)
6
y
5
4
3
2
1
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1 Distance
-2
-3
-4
-5
-6
What can you conclude from this pattern?

4. Equation of Circle with Centre (0, 0)
6
y By applying Pythagoras theorem,
5
Distance
4
3
2
As the centre of the circle (0, 0)
1 and the radius OD, then the
x equation of the circle:
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1
-2
-3
-4
-5
-6

5. Find an equation of the circle with center at (0, 0) that
passes through the point (-1, -4).
Since the center is at (0, 0) we'll have 6
y
2 2 2
x y r 5
4
The point (-1, -4) is on the circle then 3
we may substitute the coordinate on 2
the equation to find the radius of the 1
circle x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
2 2 2 -1
1 4 r -2
1 16 17 -3
-4
Subbing this in for r2 we have: -5
-6
2 2
x y 17

6. Equation of Circle with Centre (a, b)
6
y
5
4
3
2
1
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1
Distance
-2
-3
-4
-5
-6

7. Equation of Circle with Centre (a, b)
By applying distance formula,
6
y Distance
5
4
3 As the centre of the circle (a, b)
2
and the radius OD, then the
equation of the circle:
1
x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1
-2
-3
-4
-5
-6

8. Find an equation of the circle with center at (2, -1) and
radius 4.
Substitute the center and the radius into 6
the general equation y
5
4
2 -1 4 3
2
Expand and simply the equation to 1
x
give alternative form: -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
-1
-2
-3
-4
-5
-6