This document contains definitions and proofs about natural numbers, functions, and theorems in Coq. It defines natural numbers as inductive types, defines addition as a recursive function, and proves theorems like 1+1=2. It also contains definitions for monads and proofs about monad bind being associative in Coq.

1. (Kinokkory@shiatsumat)

2. C
int
double
char
T T*
T const T

4. Haskell
C++ /
Java / Python

9. ↔
↔

14. 1+1=?

15. 1+1=2

17. 1
1
2

18. “1” “ 1 ”
“+” “
”

19. “1” “2” “+” “=”

20. Coq

21. Inductive Nat:Set :=
| O : Nat
| S : Nat -> Nat.
Nat (0 )
S
(1+)
0, 1, 2, 3, ... O, S O,
S (S O), S (S (S O)), ...

22. Fixpoint Plus(m n:Nat):Nat :=
match m with
| O => n
| S m' => S (Plus m' n)
end.
Infix + := Plus.
0+n=n,
(1+m’)+n=1+(m’+n)

23. Theorem OnePlusOneEqualsTwo:
S O + S O = S (S O).
Proof.
simpl.
reflexivity.
Qed.
1+1=2

24. ......
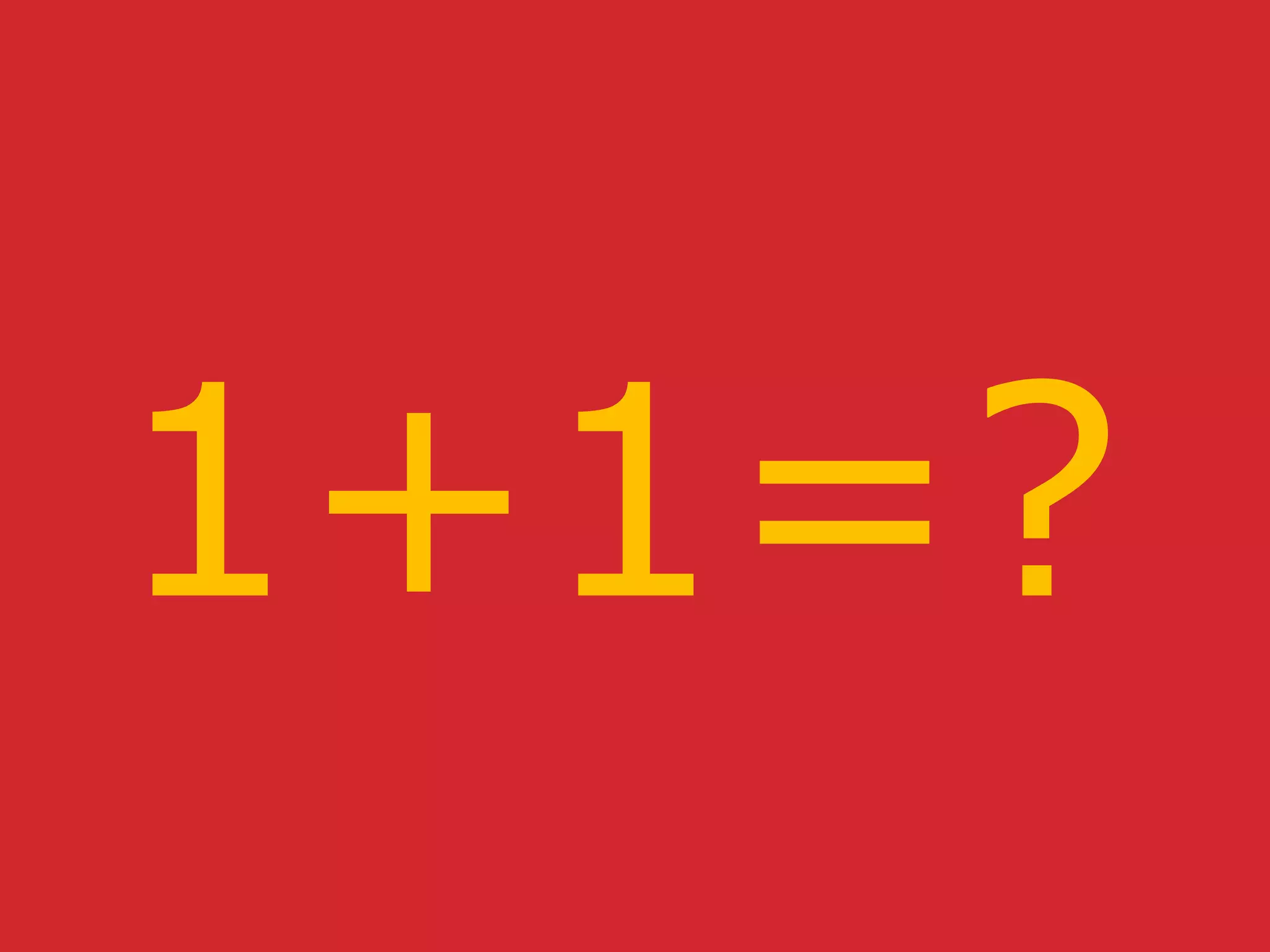
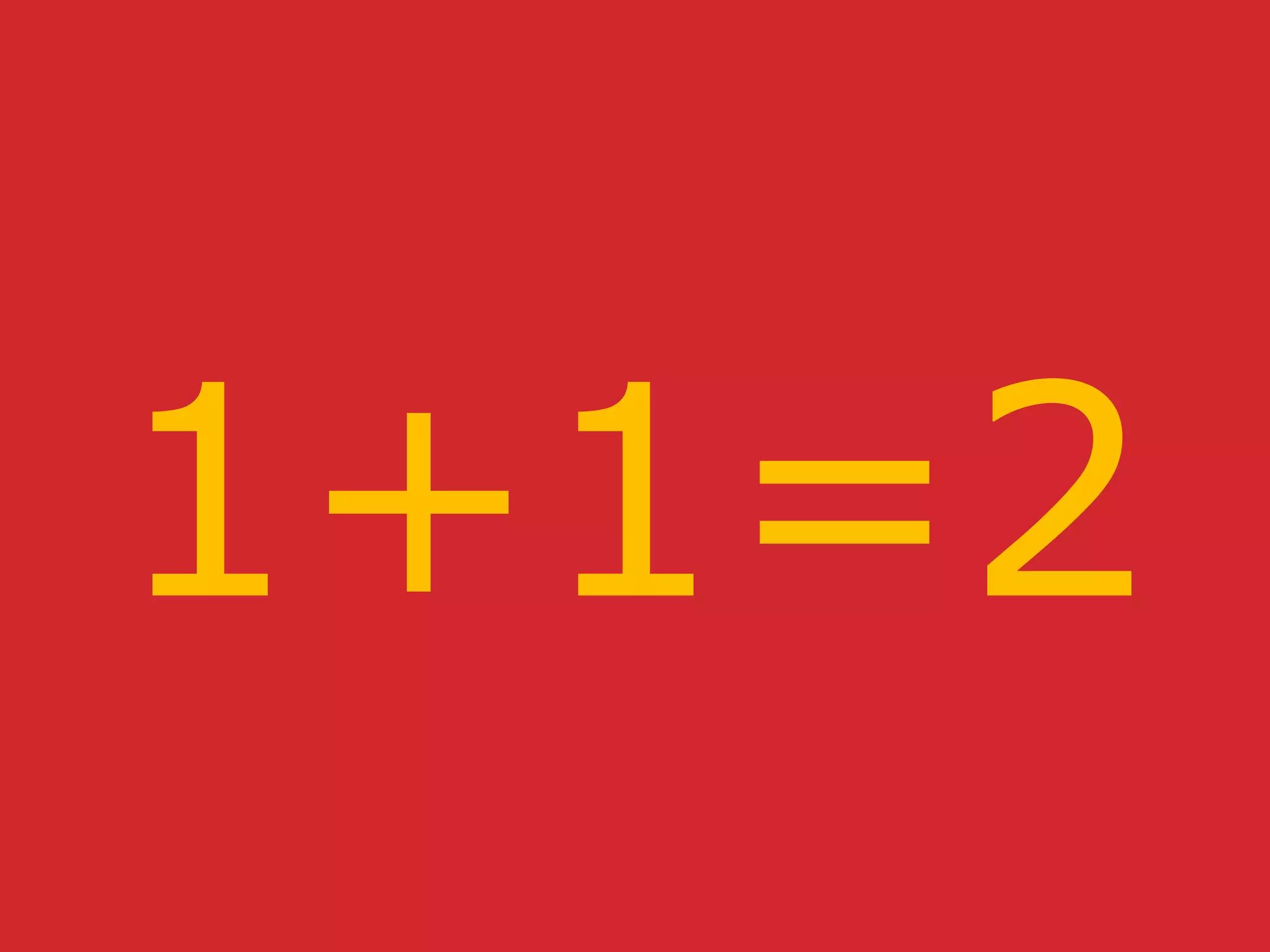
Lemma reduce_lemma :
forall ctx (ctx' : seq (term * typ)) t ty,
typing ([seq Some p.2 | p <- ctx'] ++ ctx) t ty ->
Forall (fun p => reducible ctx p.1 p.2) ctx' ->
reducible ctx (substitute_seq 0 [seq p.1 | p <- ctx'] t) ty.
Proof.
move => ctx ctx' t ty; elim: t ty ctx ctx'.
- move => /= n ty ctx ctx'.
rewrite /substitute_seqv typvar_seqindex subn0 size_map shiftzero.
elim: ctx' n => [| c' ctx' IH []] /=.
- move => n H _; rewrite nth_nil subn0.
apply CR3 => //.
- by constructor.
- move => t' H0; inversion H0.
- by case => H [H0 H1]; rewrite H.
- by move => n H [H0 H1]; apply IH.
- move => tl IHtl tr IHtr ty ctx ctx' H H0.
inversion H; subst => {H}.
case: (IHtl (tyfun ty1 ty) ctx ctx') => //= H1 H2; split; auto.
apply typapp with ty1 => //.
apply subject_substitute_seq => //.
by rewrite drop0; move: H0; apply Forall_impl => p [].
- move => t IHt ty ctx ctx' H H0.
inversion H; subst => {H} /=.
apply abstraction_lemma.
- constructor.
apply subject_substitute_seq => //.
by rewrite /= drop0; move: H0; apply Forall_impl => p [].
- move => t2 ctx2 H H1.
rewrite substitute_seq_cons_eq.
apply (IHt ty2 ctx2 ((t2, ty1) :: ctx')) => /=.
- move: H3; apply ctxleq_preserves_typing.
move: H; apply (ctxleq_appl (Some ty1 :: _)).
- split => //.
move: H0; apply Forall_impl => p.
by apply ctxleq_preserves_reducibility.
Qed.
Theorem typed_term_is_snorm : forall ctx t ty, typing ctx t ty ->
SNorm t.
Proof.
move => ctx t ty H.
apply (@CR1 ctx t ty).
move: (@reduce_lemma ctx [::] t ty H) => /=.
by rewrite substitute_seq_nil_eq; apply.
Qed.

25. Theorem monad_bind_assoc
: forall{t1 t2 t3:TypeWithEquality}
(ma:TWE_Type (m t1))
(k:TWE_Type (t1 -> m t2)%TypeWithEquality)
(h:TWE_Type (t2 -> m t3)%TypeWithEquality),
TWE_Equality (m t3)
(AWE_Arrow (AWE_Arrow bindM ma)
(Build_ArrowWithEquality (fun x => AWE_Arrow (AWE_Arrow bindM (AWE_Arrow k x)) h)
(fun (x y : TWE_Type t1) (Hxy : TWE_Equality t1 x y) =>
AWE_Compat bindM
(AWE_Arrow k x)
(AWE_Arrow k y)
(AWE_Compat k x y Hxy)
h
h
(Equivalence_Reflexive(Equivalence:=TWE_Equivalence _) h)
)
)
)
(AWE_Arrow (AWE_Arrow bindM (AWE_Arrow (AWE_Arrow bindM ma) k)) h).
Proof.
intros.
intros x y H.
unfold bindM,returnM; simpl.
apply (AWE_Compat ma).
simpl.
intros x0 y0 H0.
assert (HEql: TWE_Equality _ (AWE_Arrow k x0) (AWE_Arrow k y0)).
apply (AWE_Compat k).
apply H0.
apply HEql.
simpl.
intros x1 y1 H1.
assert (HEql2: TWE_Equality _ (AWE_Arrow h x1) (AWE_Arrow h y1)).
apply (AWE_Compat h).
apply H1.
apply HEql2.
apply H.
Qed.
End ContinuationMonadBase.
Module FContinuationMonadBaseBase <:HasReturnType.
Definition ReturnType : TypeWithEquality := TypeWithEquality_eq False.
End FContinuationMonadBaseBase.
Module FContinuationMonadBase := FContinuationMonadBaseBase <+ ContinuationMonadBase.
Maybe

27. Coq