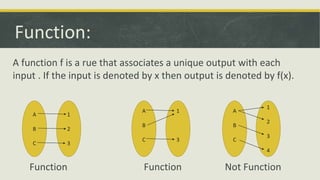
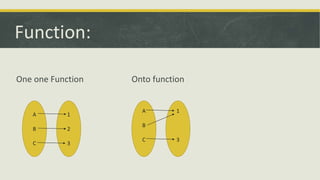
A function f associates a unique output with each input. The input is denoted as x and the output is denoted as f(x). The domain of a function f is the set of all allowable input values, while the range is the set of all output values. An inverse function f-1 can be written if f is one-to-one and onto. The composition of two functions f and g, denoted as fog and gof, are defined as fog=f(g(x)) and gof=g(f(x)).

1. Submitted by :
Md sadiquzzaman
ID-163002017
Dep Of CSE

2. Function

3. Function:
A function f is a rue that associates a unique output with each
input . If the input is denoted by x then output is denoted by f(x).
A
B
C
1
2
3
A
B
C
1
3
A
B
C
1
2
3
4
Function Function Not Function

4. Function:
A
B
C
1
2
3
A
B
C
1
3
One one Function Onto function

5. Inverse Function :
If y=f(x) be one-one and onto function then it
can be written as x= f-1(y) here f-1 is called
inverse of f .

6. Composition function :
If f and g be two functions of x then the composition
of ‘f’ with ‘g’ and ‘g’ with ‘f’ are denoted by fog and
gof . These are define as
gof= g(f(x))
and
fog=f(g(x))

7. Example of Composition Function :
If f(x)=x2+3 and g(x)= 𝑥 then find fog and gof ?
Solution:
fog = f(g(x)) gof =g(f(x))
= f( 𝑥) =g(x2+3)
= ( 𝑥)2+3 = 𝑥^2 + 3
= x+3

8. Domain and Range :
If x an y are related by the equation
y=f(x) then the set if all allowable input
(x-values) called the domain of ‘f’ and the
setoff output (y-values) called the range
of ‘f’.

9. Domain and Range Example :
A function f:{0,1,2,3}{2,5,8,11,15} is defined by
f(x)=3x+2 then find domain codomain and range?
Solution:
Dom f ={0,1,2,3}
Co Dome f={2,5,8,11,15}
Range f = {f((0),f(1),f(2),f(3)}
={2,5,8,11}