This document is a presentation in Russian given by Yevgeniy Kurbakey about dependent types. It discusses the motivation for dependent types, provides examples of dependent types in Idris including vectors of fixed length and natural numbers, demonstrates type checking and static verification, and shows how dependent types enable constructive mathematics with proofs built into types and terms.

1. Çà÷åì íóæíû çàâèñèìûå òèïû
Åâãåíèé Êóðáàöêèé
JetBrains
2013
1 / 27

2. Çà÷åì íóæíû çàâèñèìûå òèïû
÷òî òàêîå çàâèñèìûé òèï
ñïèñêè ôèêñèðîâàííîé äëèííû
áåçîïàñíûé printf
êîíñòðóêòèâíàÿ ìàòåìàòèêà
ñòàòè÷åñêèå ïðîâåðêè
2 / 27

3. Çàâèñèìàÿ ôóíêöèÿ
(x : A) → B (x )
f : (x : Bool) -> (if x then String else Int)
f True = "42"
f False = 42
3 / 27

4. Òèïû òèïîâ
òèï ÿâëÿåòñÿ âûðàæåíèåì
5 : Int
Int : Type
Int -> Int : Type
5 : (if False then String else Int)
(x : Bool) ->
(if x then String else Int) : Type
"What?" : if (isPrime 2147483647) then
String else Int
4 / 27

5. Ïðîâåðêà òèïîâ
Òîòàëüíûå ôóíêöèè
ôóíêöèÿ âñåãäà çàâåðøàåòñÿ
ôóíêöèÿ âñåãäà âîçâðàùàåò çíà÷åíèå
5 / 27

6. Idris
ïîääåðæèâàåò çàâèñèìûå òèïû
ñèíòàêñèñ ïîõîæ íà Haskell
íå ëåíèâûå âû÷èñëåíèÿ
àêòèâíî ðàçðàáàòûâàåòñÿ
â äîêëàäå èñïîëüçîâàííà âåðñèÿ 0.9.8
6 / 27

7. Íàòóðàëüíûå ÷èñëà
data Nat : Type where
Z : Nat
S : Nat - Nat
(+) : Nat - Nat - Nat
Z
+ y = y
(S k) + y = S (k + y)
7 / 27

8. Ñïèñêè ôèêñèðîâàííîé äëèííû
data List : Type - Type where
Nil : List a
(::) : a - List a - List a
data Vect : Type - Nat - Type where
Nil : Vect a Z
(::) : a - Vect a k - Vect a (S k)
app : Vect a n - Vect a m - Vect a (n + m)
app Nil ys = ys
app (x :: xs) ys = x :: app xs ys
8 / 27

9. Ñïèñêè ôèêñèðîâàííîé äëèííû
data Vect : Type - Nat - Type where
Nil : Vect a Z
(::) : a - Vect a k - Vect a (S k)
Nil : Vect Int Z
(1 :: 2 :: 3 :: Nil) : Vect Int (S S S Z)
IntVect : Nat - Type
IntVect = Vect Int
(1 :: 2 :: Nil) : IntVect (S S Z)
9 / 27

10. Ñïèñêè ôèêñèðîâàííîé äëèííû
data Vect : Type - Nat - Type where
Nil : Vect a Z
(::) : a - Vect a k - Vect a (S k)
head : Vect a (S k) - a
head (h :: t) = h
head (1 :: 2 :: 4 :: Nil)
head Nil
defaultHead : Vect a k - a - a
defaultHead Nil default = default
defaultHead v _ = head v
10 / 27

11. Printf
sprintf Simple!!!
sprintf Hello %s!!! world
sprintf Answer is %d 42
sprintf Mistake %s %d 42 world
sprintf Forgot %d
sprintf Too much %d 1 2
11 / 27

12. Printf
data Format = End |
FMInt Format |
FMString Format |
FMChar Char Format
parse
parse
parse
parse
parse
: List Char - Format
Nil = End
('%'::'d'::cs) = FMInt (parse cs)
('%'::'s'::cs) = FMString (parse cs)
(c::cs) = FMChar c (parse cs)
12 / 27

13. ToType
ToType
ToType
ToType
ToType
: Format - Type
End =
(FMInt rest) =
(FMString rest) =
(FMChar c rest) =
String
Int - ToType rest
String - ToType rest
ToType rest
13 / 27

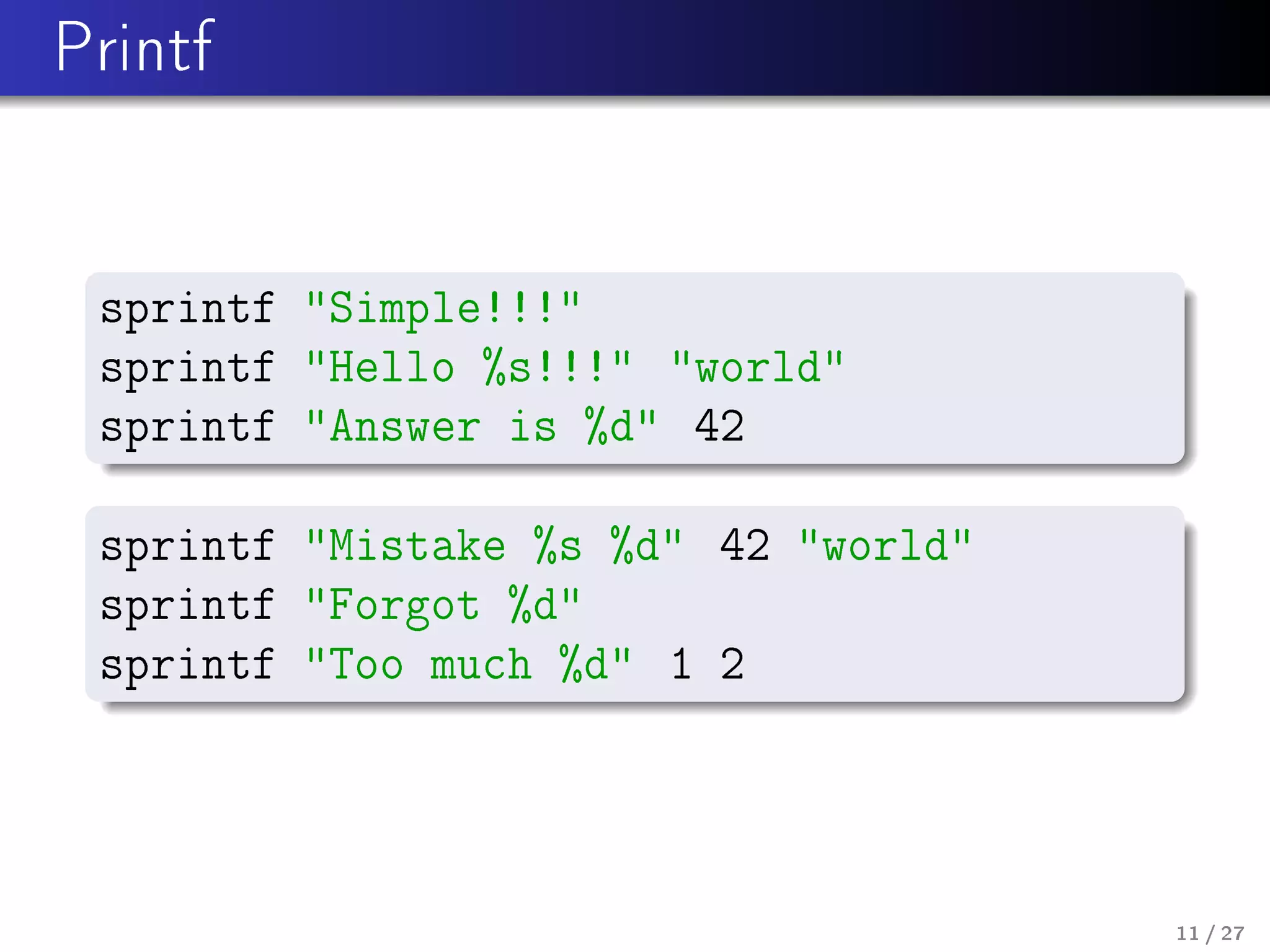
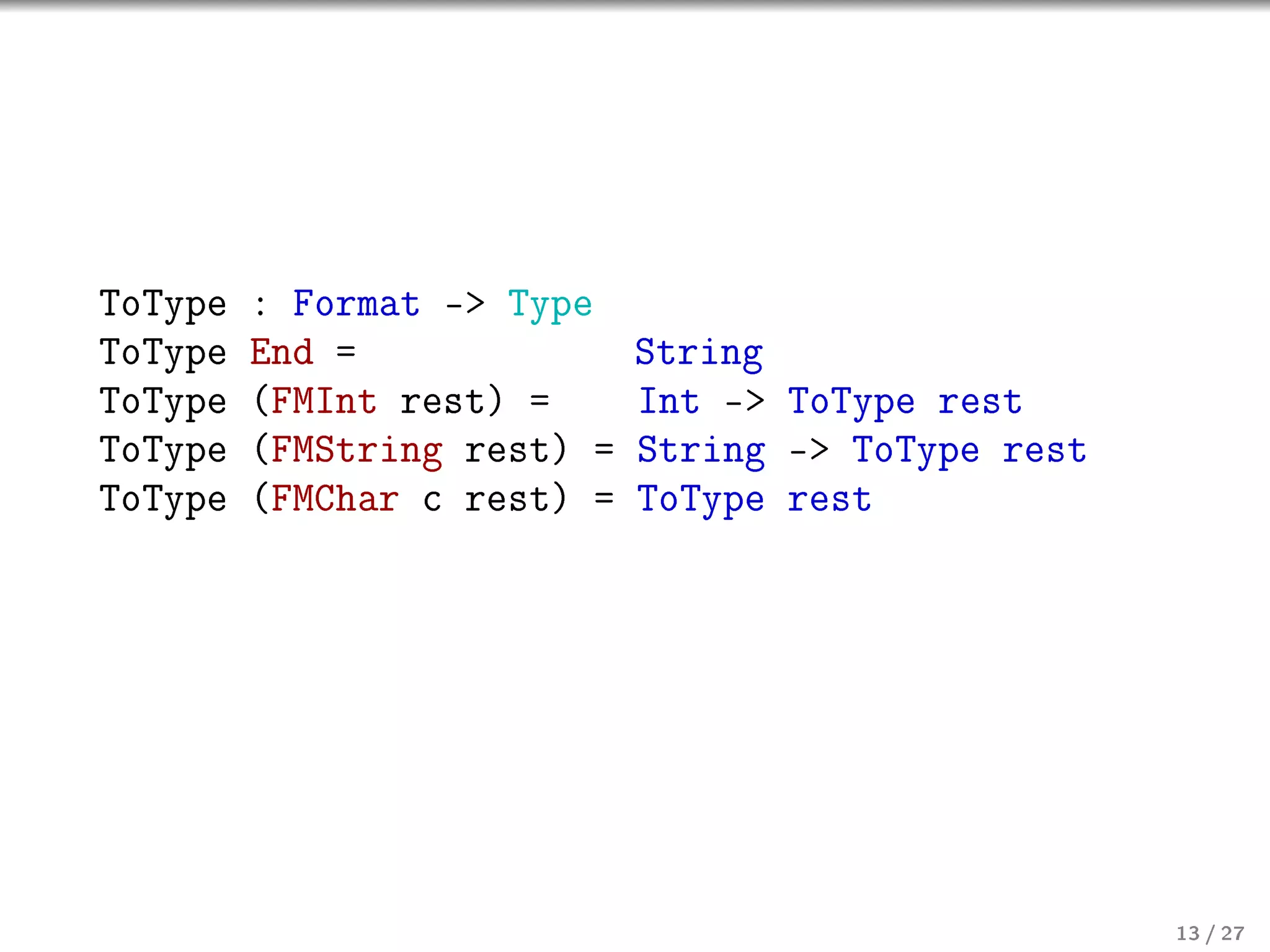
14. sprintf : (f: String) -
ToType (parse (unpack f))
sprintf fmt = prt (parse (unpack f)) Nil
prt : (f: Format) - List Char - ToType f
prt End acc =
pack acc
prt (FMInt r) acc =
i: Int = prt r (acc ++ (unpack (show i)))
prt (FMString r) acc =
s: String = prt r (acc ++ (unpack s))
prt (FMChar c r) acc =
prt r (acc ++ [c])
14 / 27

15. Çàâèñèìàÿ ïàðà
d : (x : Bool ** if x then String else Int)
d = (False ** 42)
15 / 27

16. Êîíñòðóêòèâíàÿ ìàòåìàòèêà
data Or : a - b - Type where
Inl : a - Or a b
Inr : b - Or a b
data And : a - b - Type where
mkAnd : a - b - And
data True : Type
mkTrue : True
data _|_ : Type where
Not : Type - Type
Not a = a - _|_
16 / 27

17. Êîíñòðóêòèâíàÿ ìàòåìàòèêà
Ìàòåìàòèêà
Òèïû
Äîêçàòåëüñòâî
Òåðì
Òåîðåìà
Òèï
True
False
A→B
A∧B
A∨B
¬A
∀x ∈ A B (x )
∃x ∈ A B (x )
True (Unit)
_|_
A - B
And A B (Ïàðà)
Or A B (Either)
A - _|_
(x : A) - B x
(x : A ** B x)
Èíäóêöèÿ
Ðåêóðñèÿ
17 / 27

18. Ïðèìåð
A∨B →B ∨A
Or a b - Or b a
lemma1 : Or a b - Or b a
lemma1 (Inl av) = (Inr av)
lemma1 (Inr bv) = (Inl bv)
18 / 27

19. Ïðèìåð
(
A → B ) → (B → C ) → (A → C )
(a - b) - (b - c) - (a - c)
lemma2 : (a - b) - (b - c) - (a - c)
lemma2 f1 f2 = (x = f2 (f1 x))
19 / 27

20. Ðàâåíòñâî
data (=) : t - t - Type where
refl : (a : t) - a = a
20 / 27

21. Ðàâåíòñâî
∀a1 ∈ T , ∀a2 ∈ T ,
a1 = a2 → a2 = a1
symm : (a1 : t) - (a2 : t) -
(a1 = a2) - (a2 = a1)
symm _ _ (refl a) = (refl a)
21 / 27

22. Ðàâåíòñâî
∀a ∈ T , ∀b ∈ T , ∀p (T ),
a = b → p(a) = p(b)
apply : (a : t) - (b : t) -
(p : t - t1) -
(a = b) - (p a) = (p b)
apply _ _ p (refl x) = refl (p x)
22 / 27

23. Ïðèìåð
(+) : Nat - Nat - Nat
Z
+ y = y
(S k) + y = S (k + y)
∀a, b, c ∈ N, a + (b + c ) = (a + b) + c
assoc : (a : Nat) - (b : Nat) -
(a + (b + c)) = ((a + b)
assoc Z b c = refl (b + c)
assoc (S a) b c = apply (a + (b +
((a + b) + c) S (assoc a
(c : Nat) -
+ c)
c))
b c)
23 / 27

24. Ïðîâåðêè âî âðåìÿ êîìïèëÿöèè
data so : Bool - Type where
oh : so True
test : Bool
test1 : so test
test1 = oh
test2 : so (2 * 2 == 4)
test2 = oh
testFail : so (2 * 2 == 5)
testFail = oh
24 / 27

25. Ñòàòè÷åñêèå îãðàíè÷åíèÿ
data () : Nat - Nat - Type where
lessZ : Z (S k)
lessS : k1 k2 - (S k1) (S k2)
Array : Type - Nat - Type
get: (Array a sz) - (i: Nat ** i sz) - a
25 / 27

26. lemma : i n - i (S n)
lemma lessZ = lessZ
lemma (lessS a) = lessS (lemma a)
range2 : (n : Nat) - (i : Nat) - i (S n) -
List (a : Nat ** a n)
range2 n Z lessZ = []
range2 n (S i) (lessS iln) =
(i ** iln) :: (range2 n i (lemma iln))
subList : (n : Nat) - (i : Nat) - (i S n) -
Array a n - List a
subList n i prf a = map (get a) (range2 n i prf)
26 / 27

27. Ñïàñèáî çà âíèìàíèå
Âîïðîñû?
27 / 27