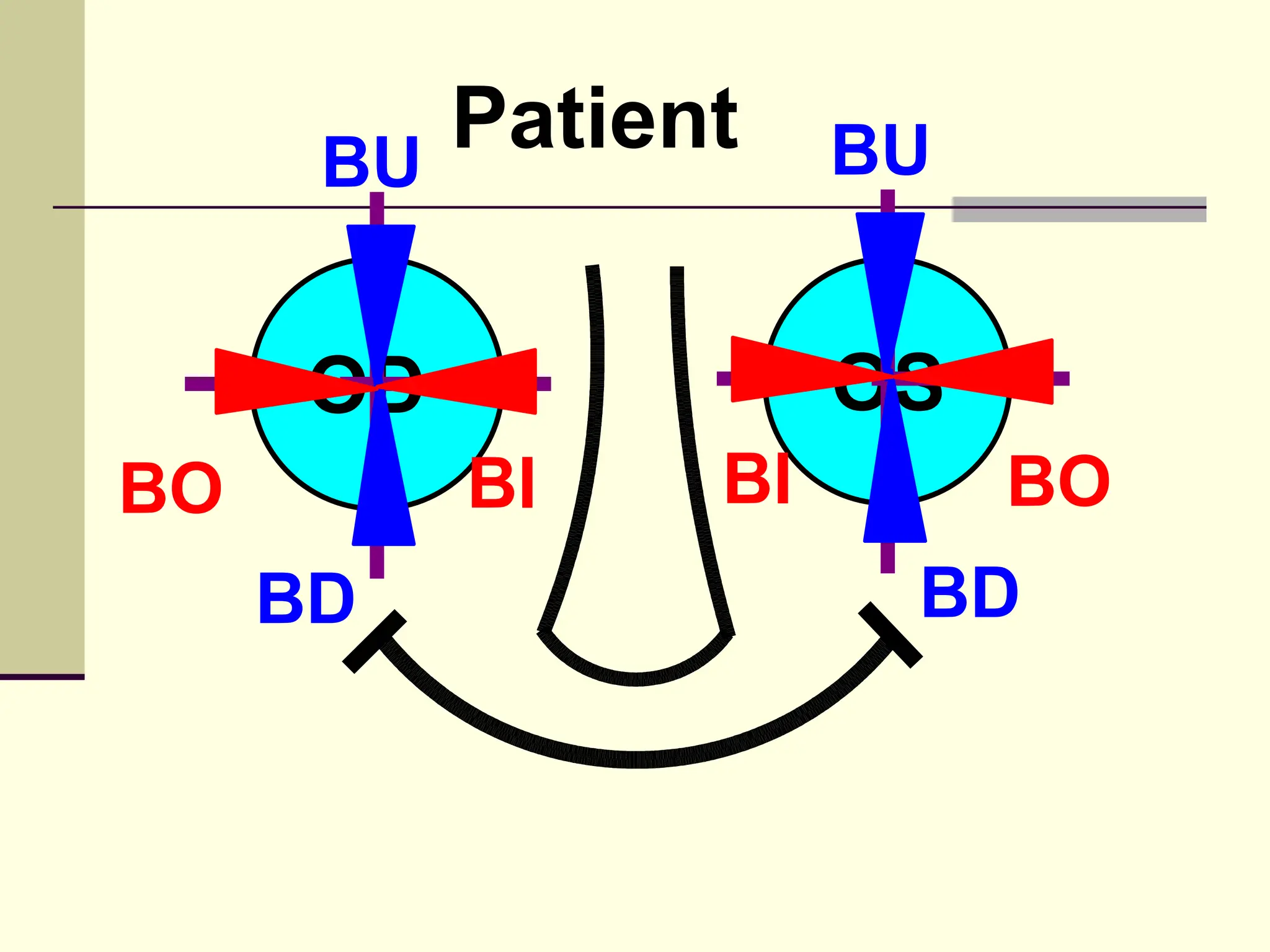
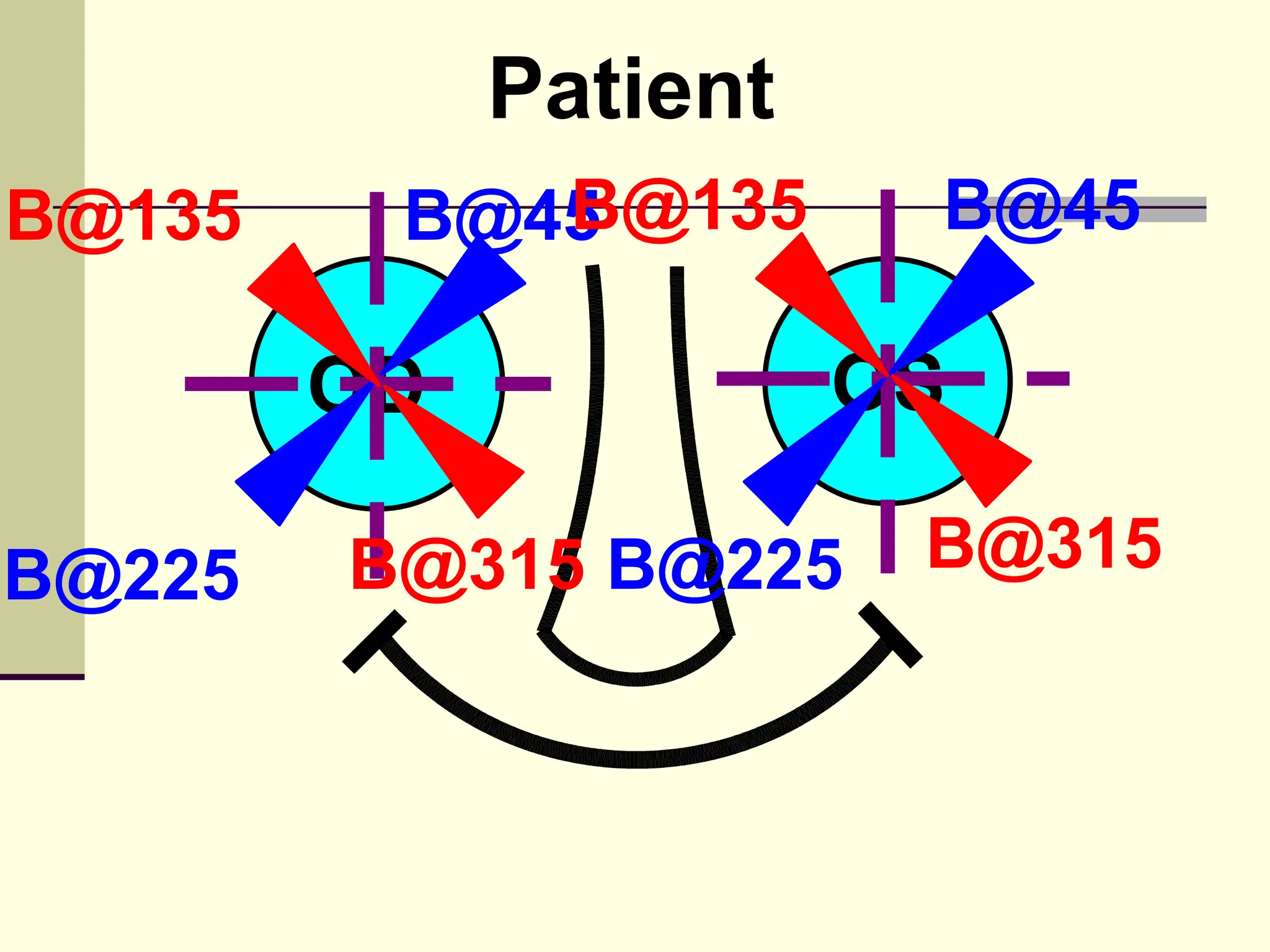
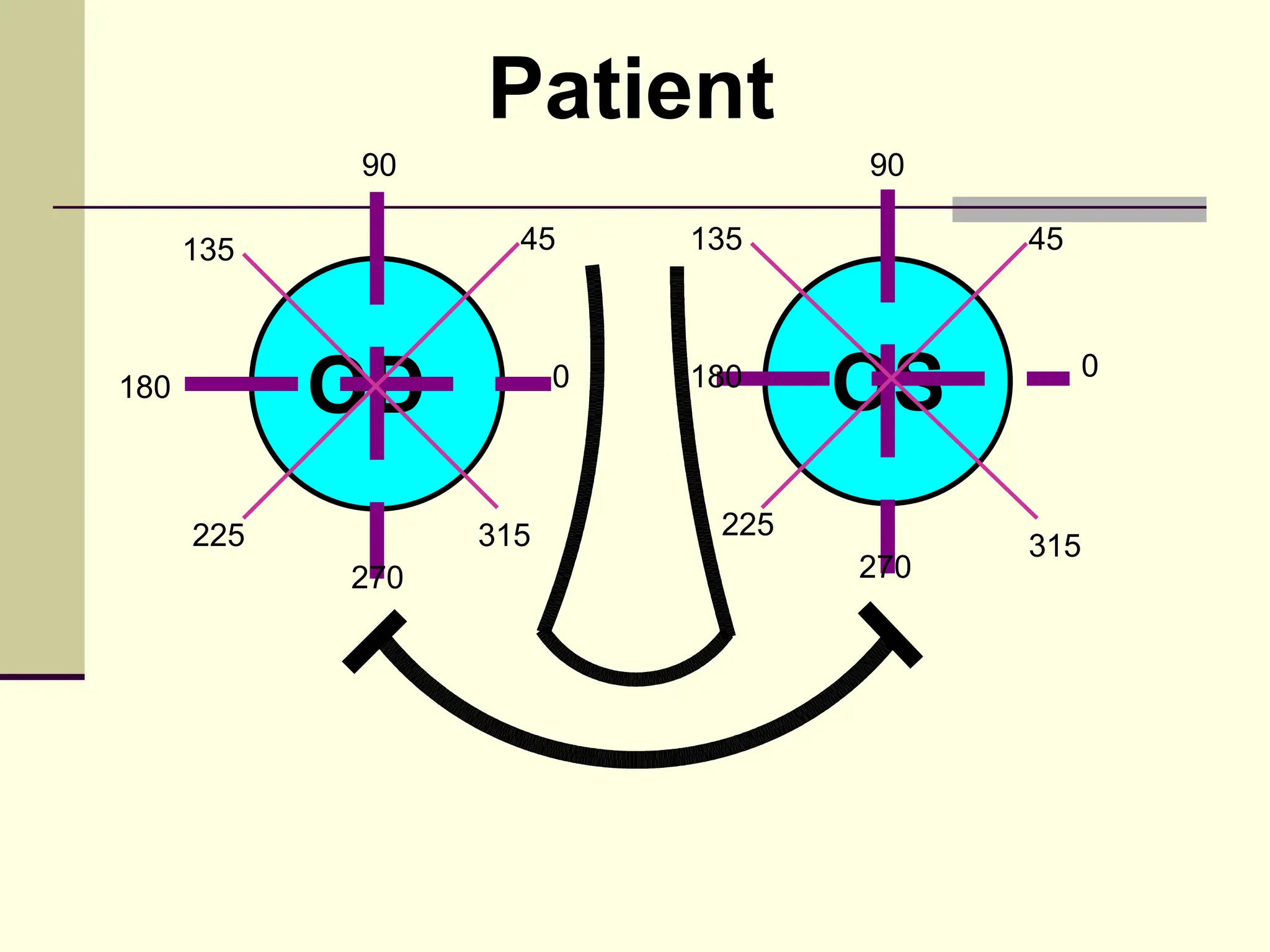
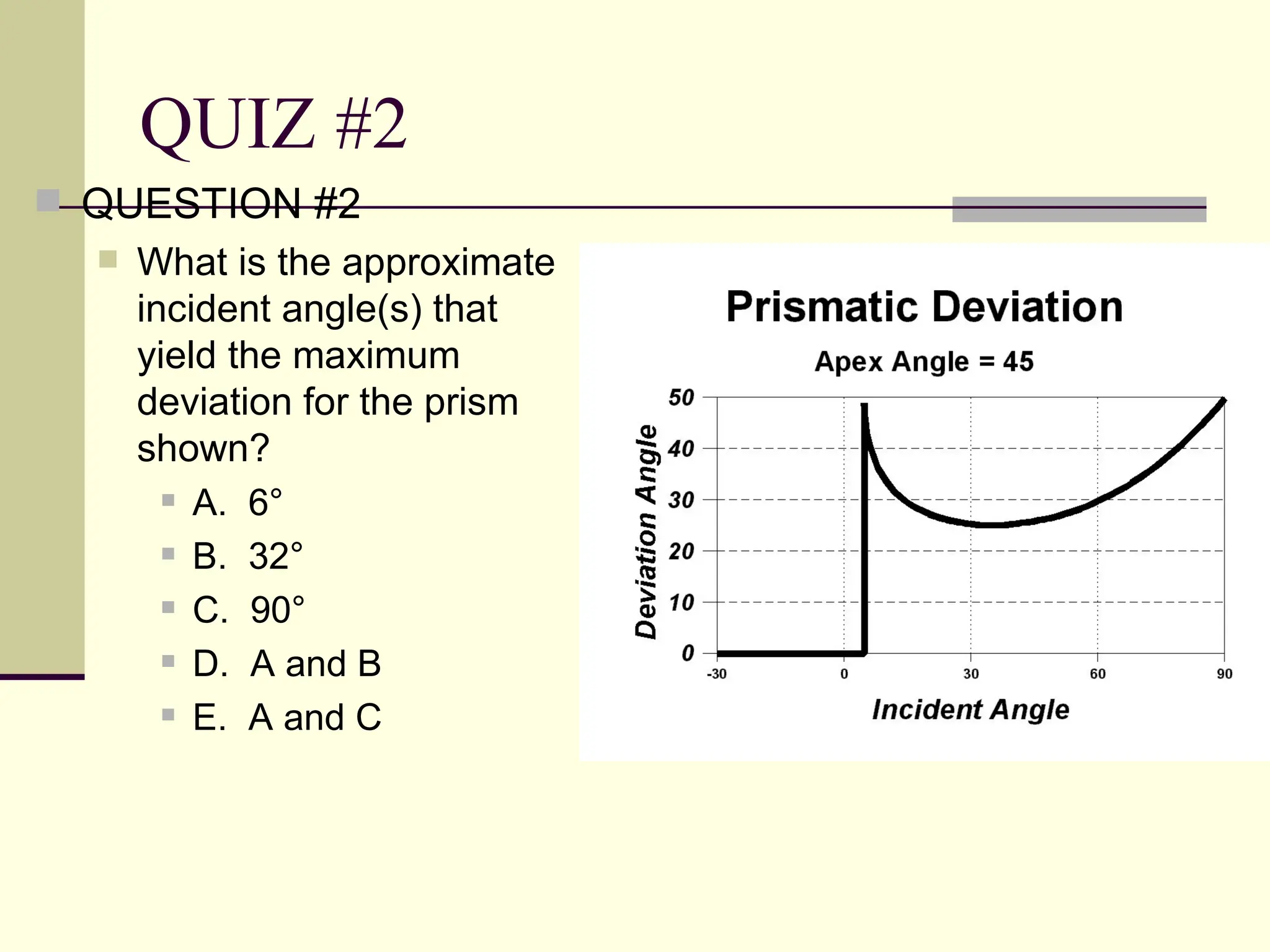
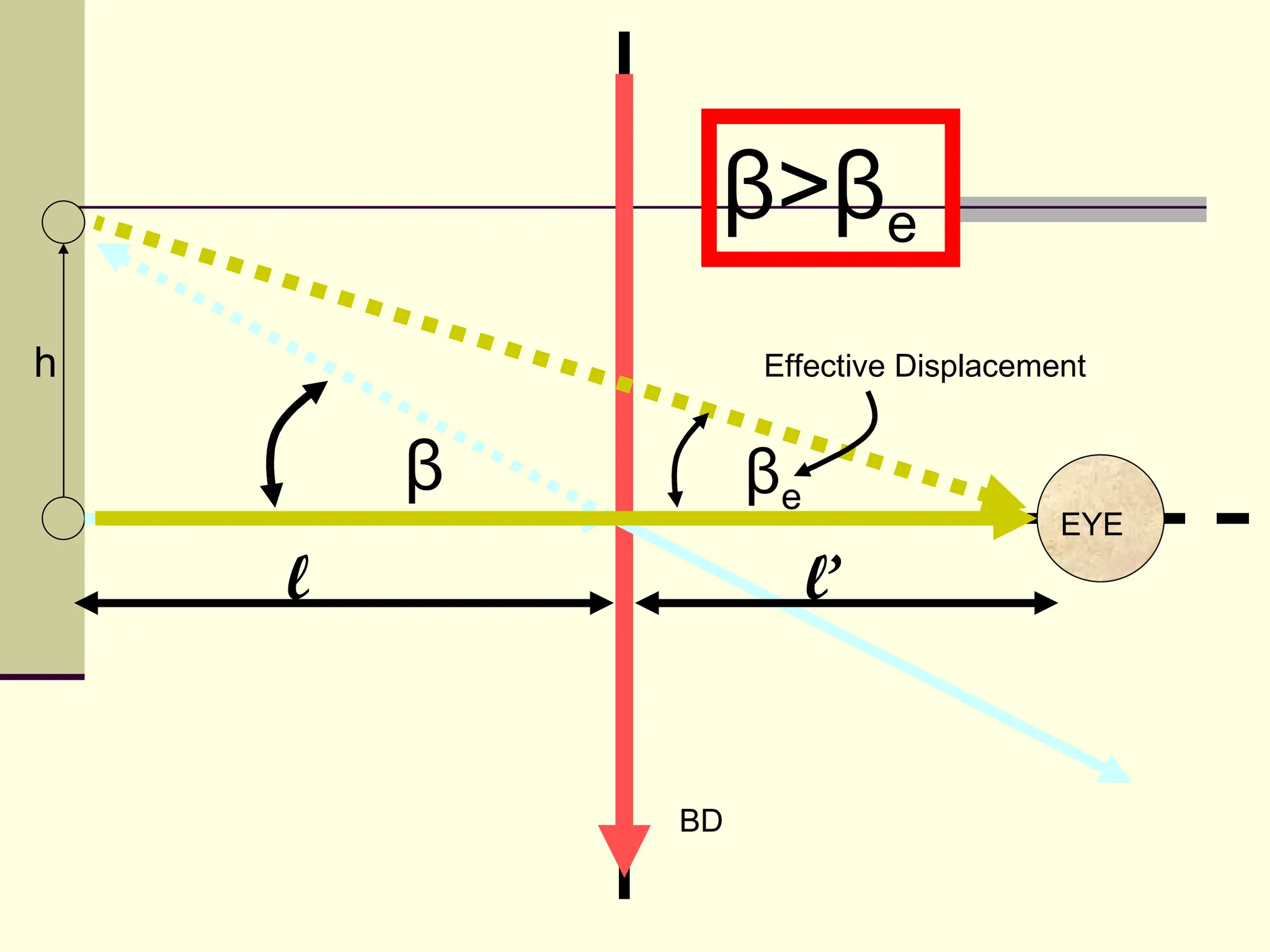
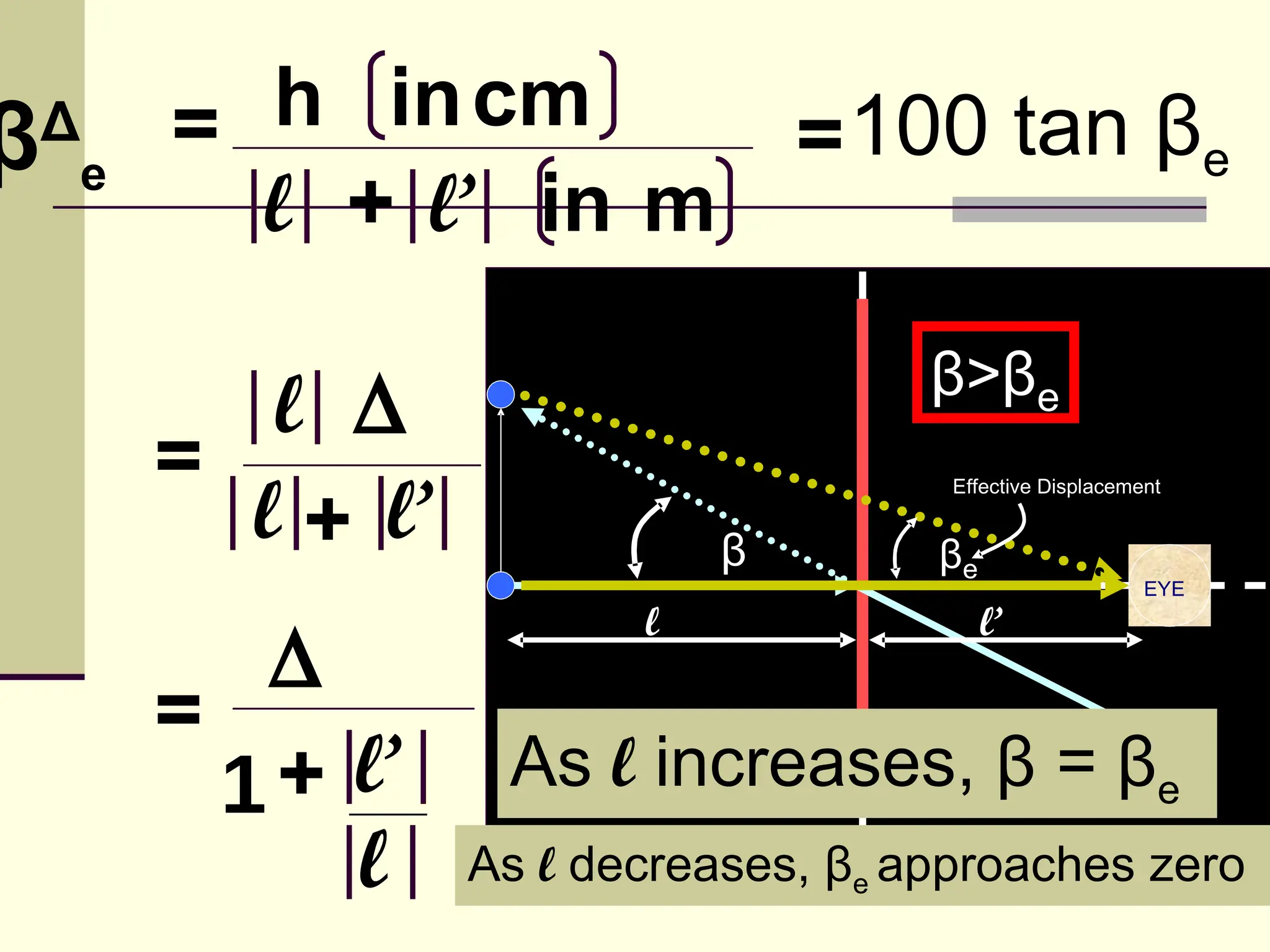
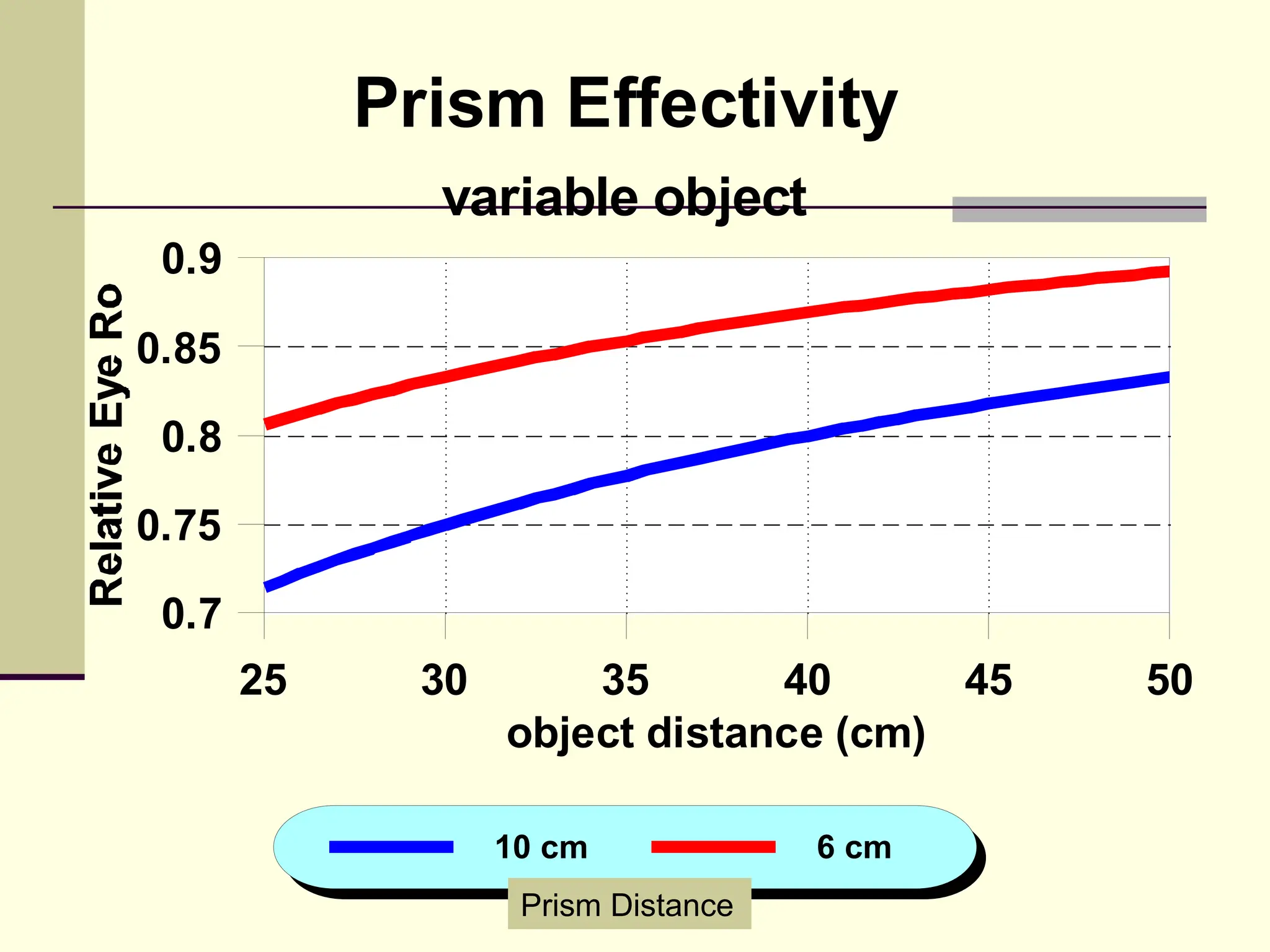
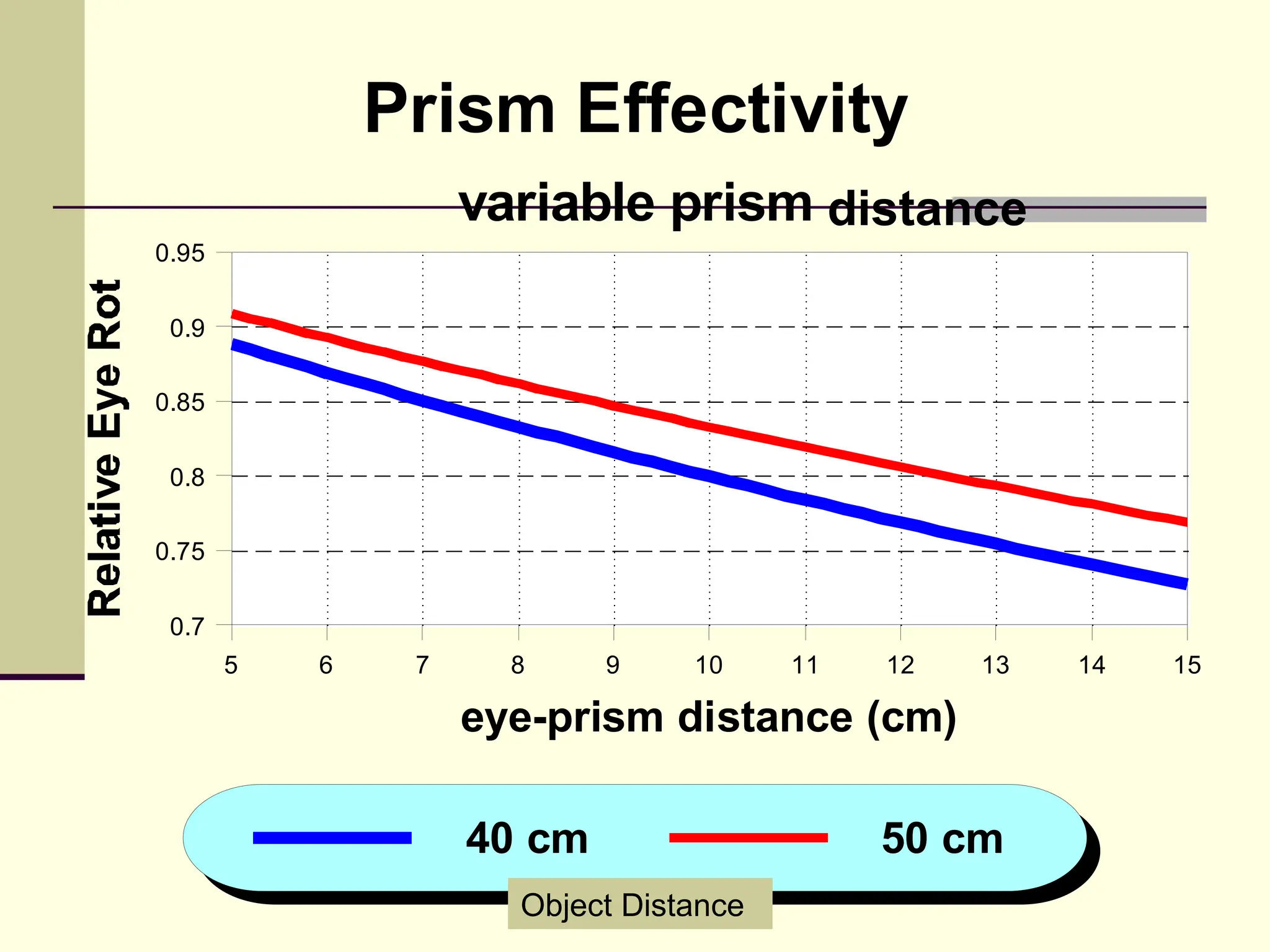
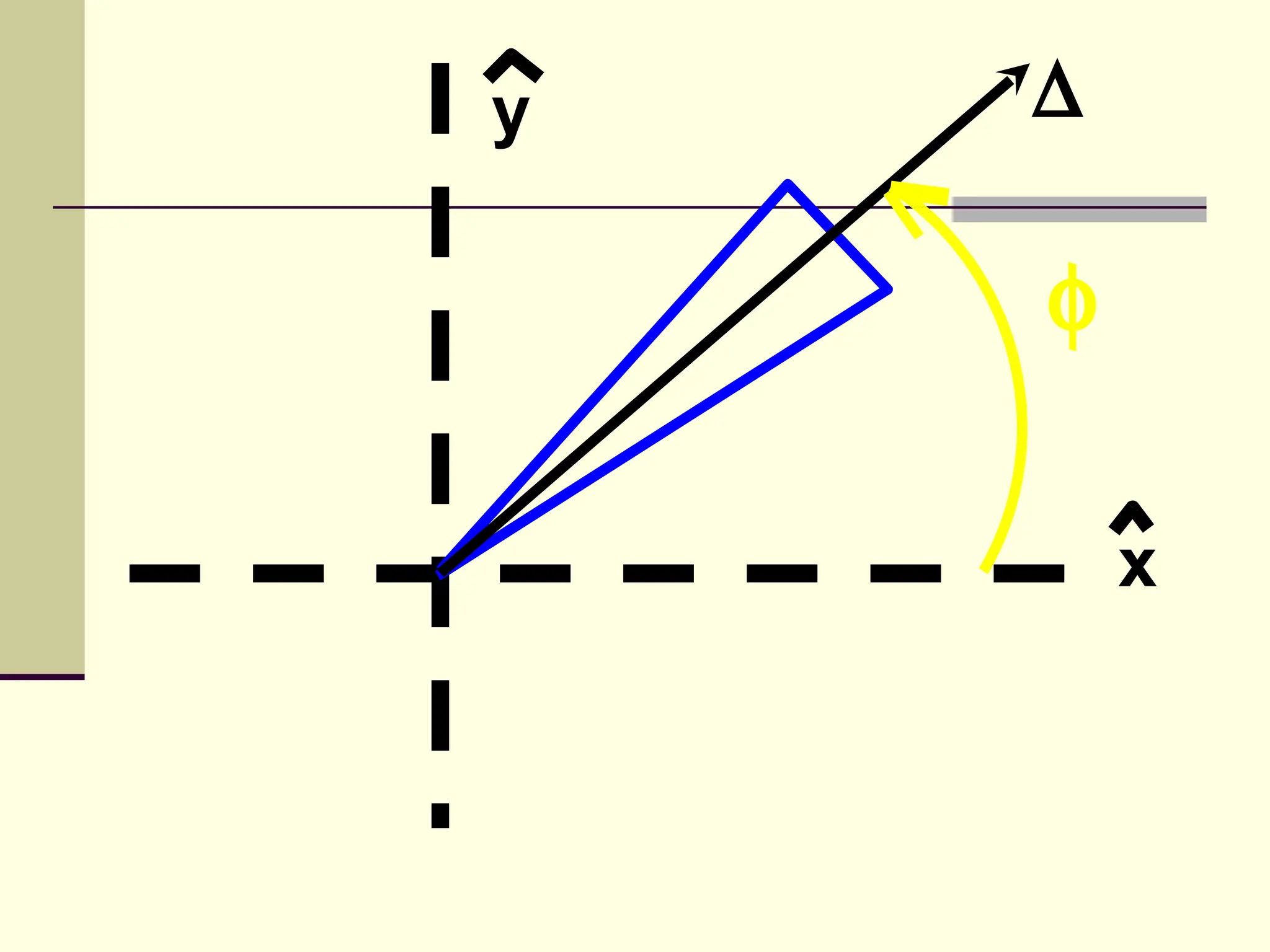
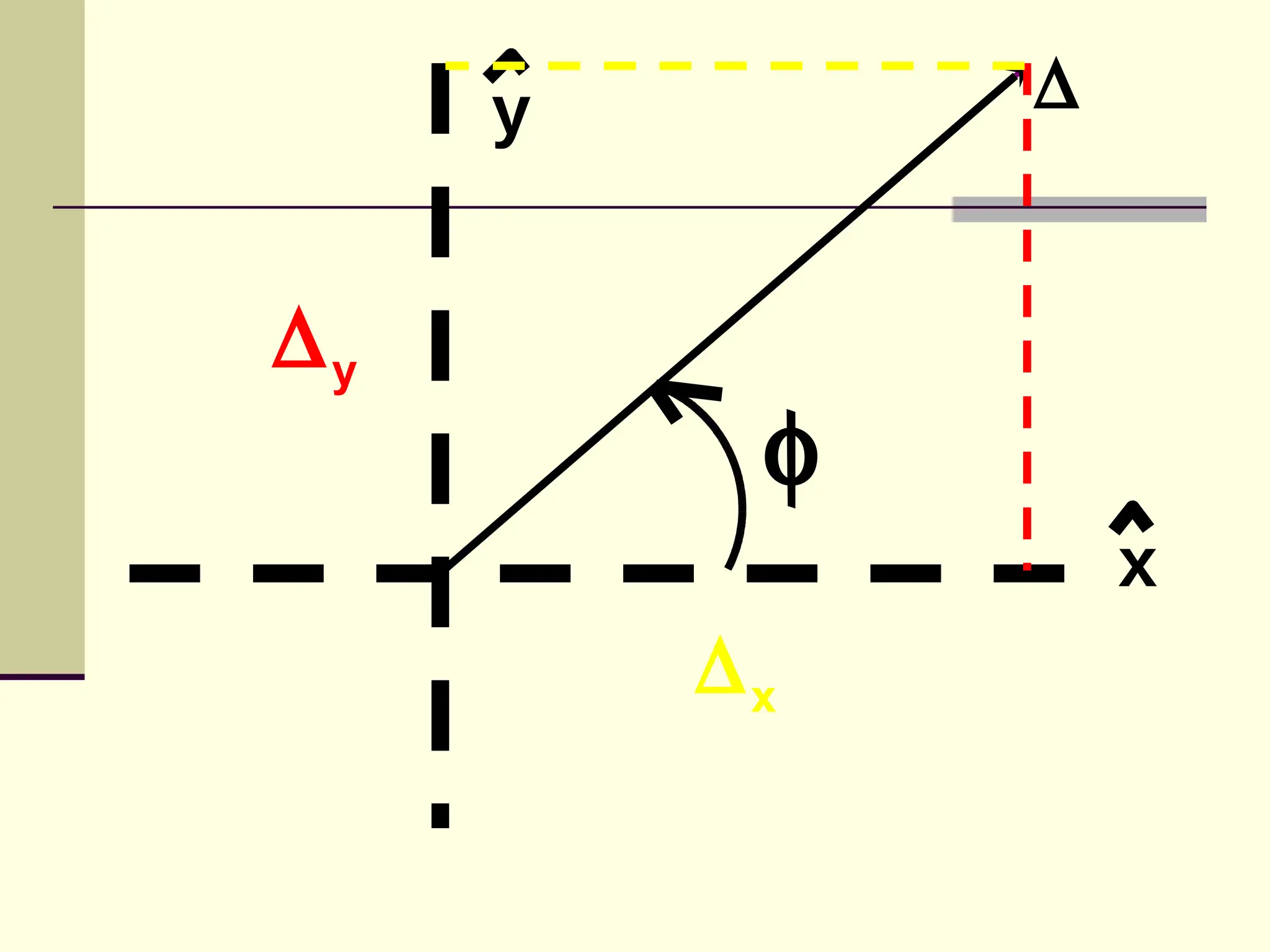
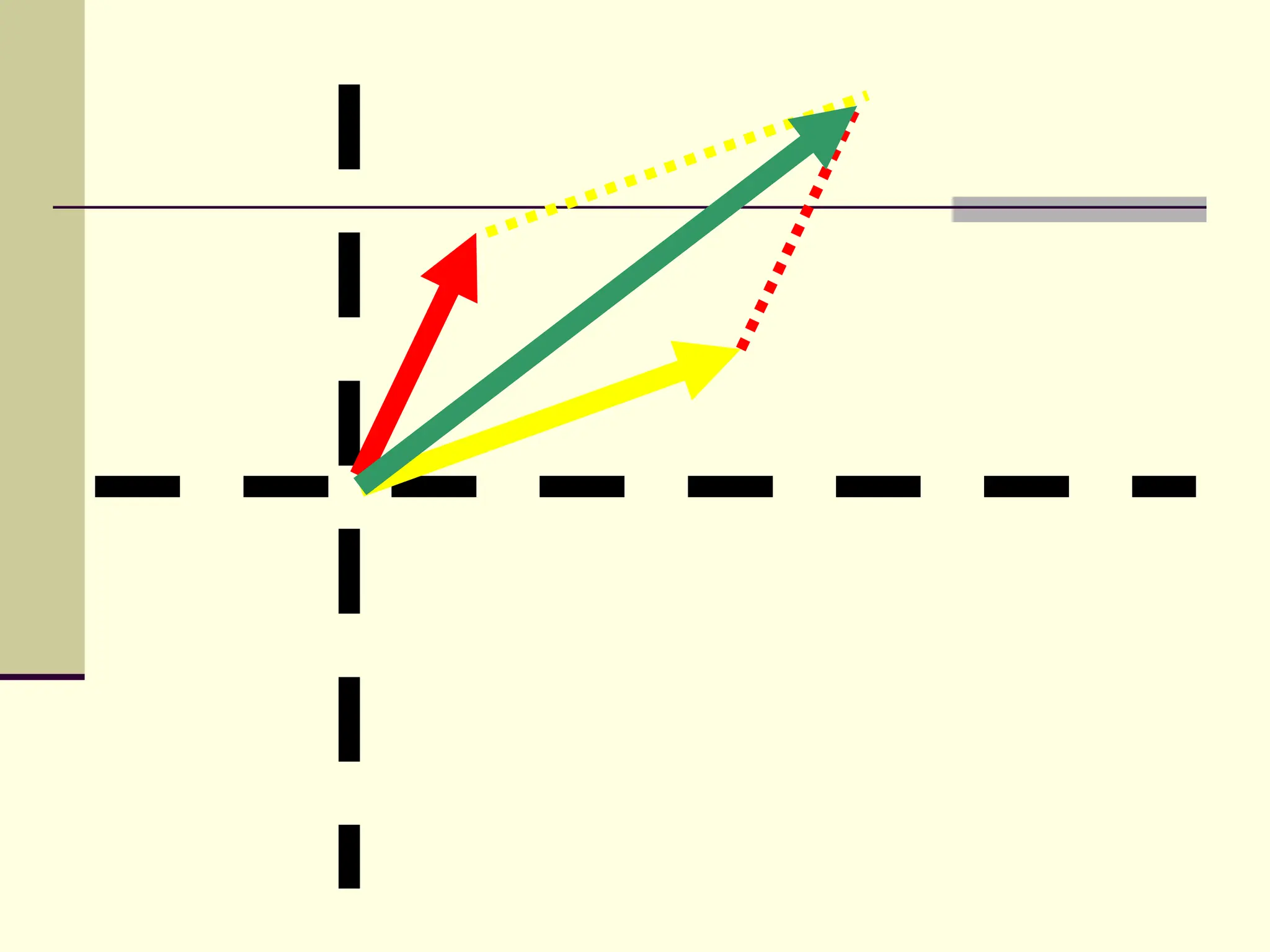
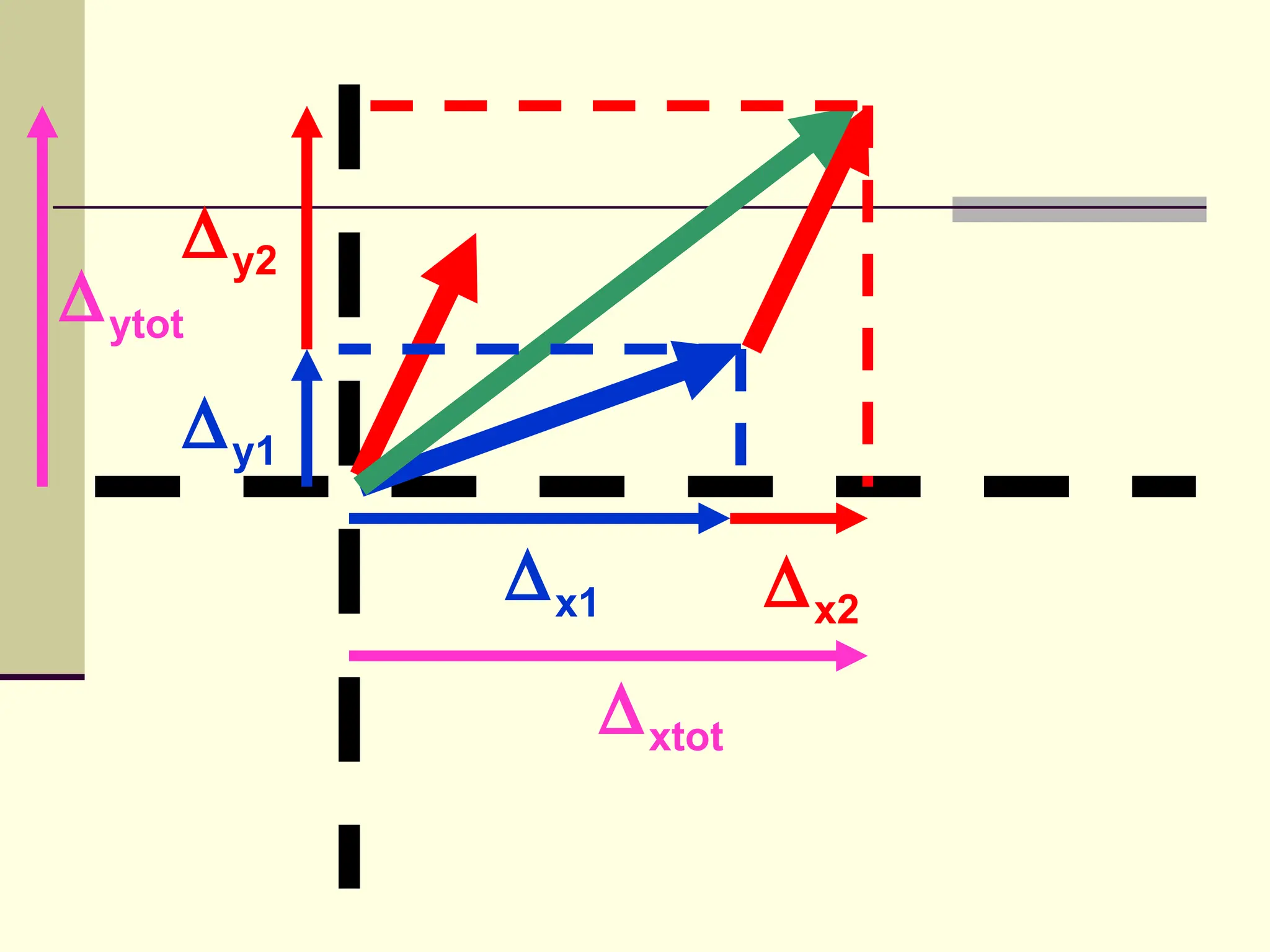
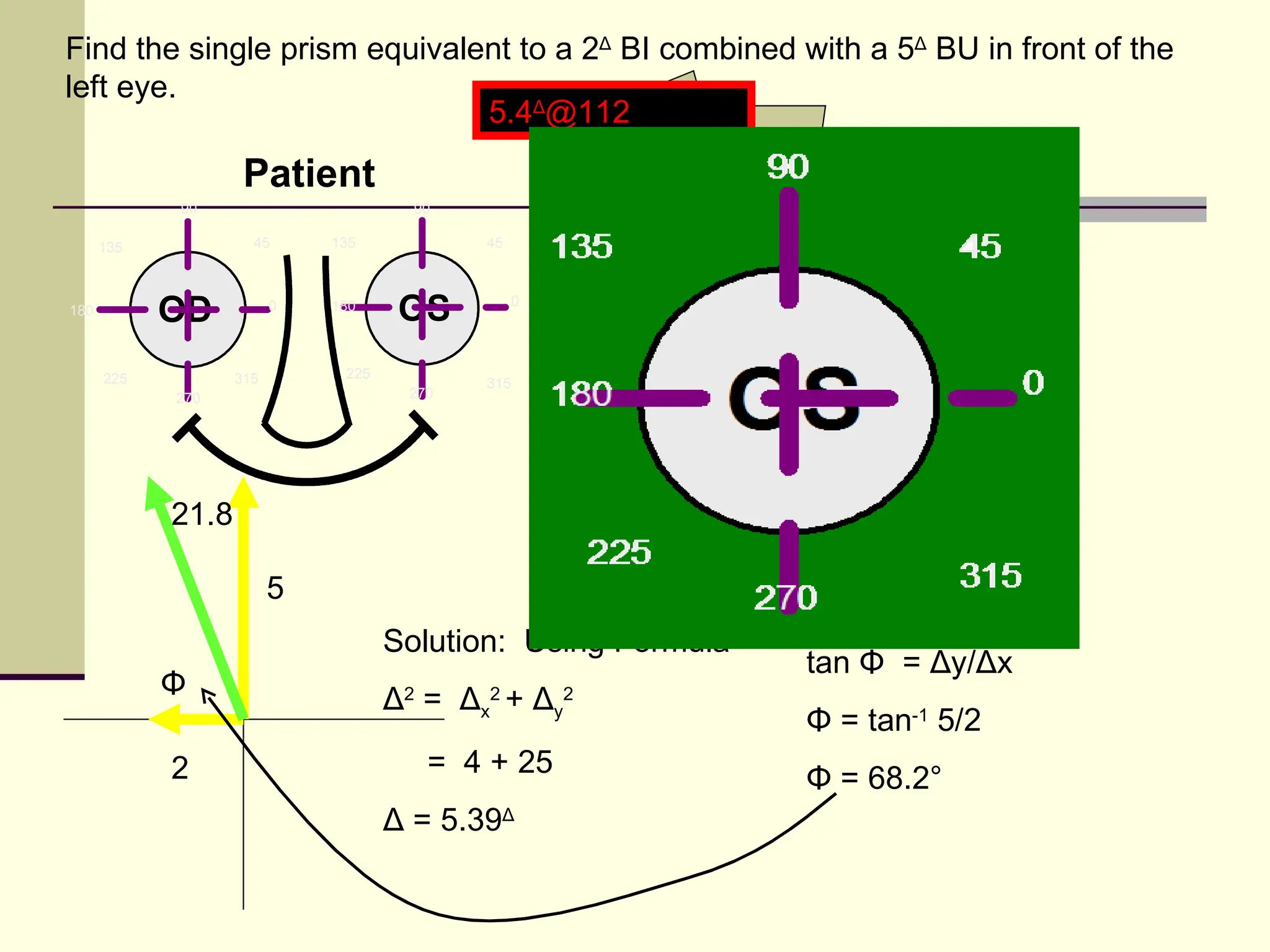
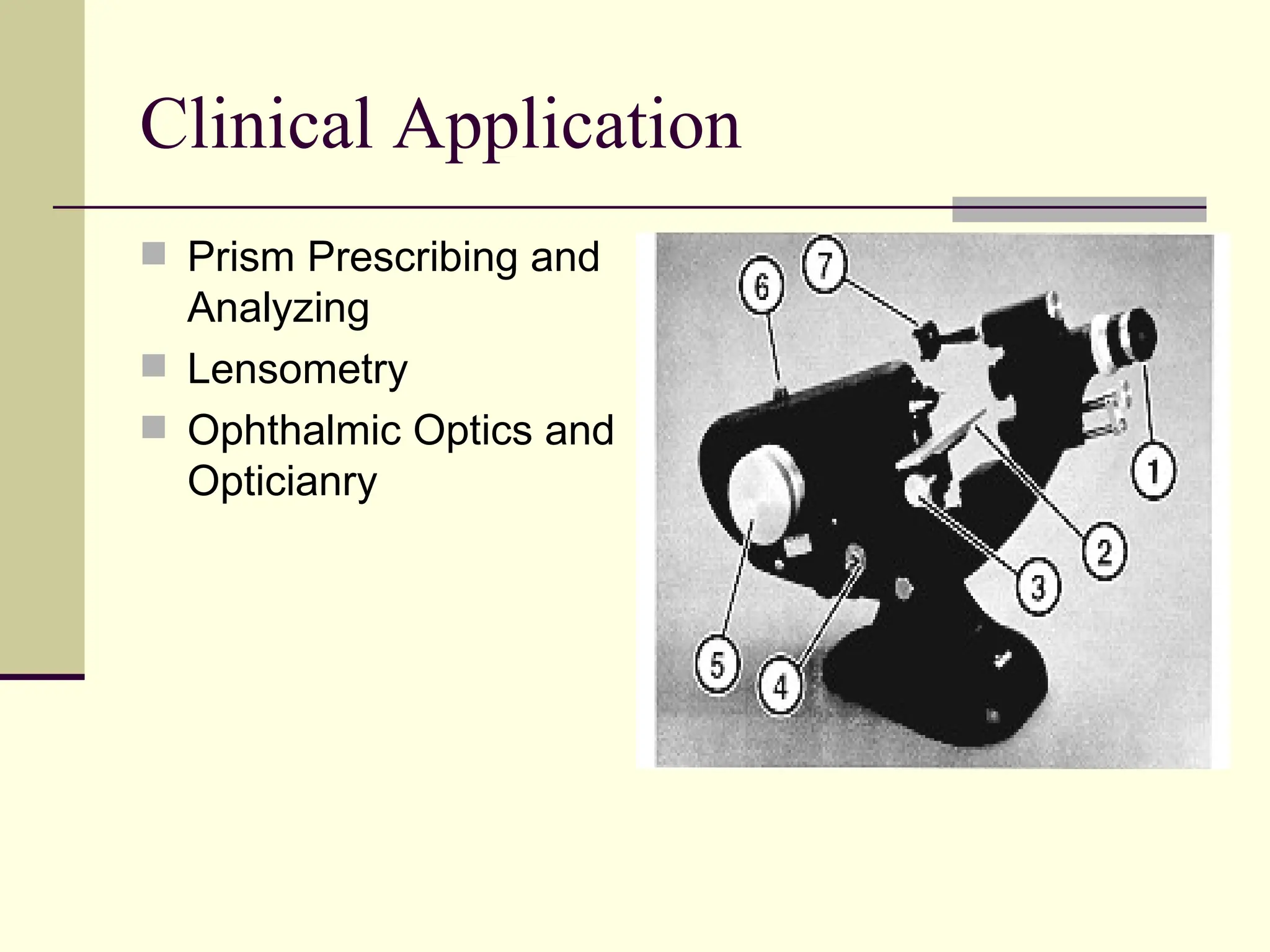
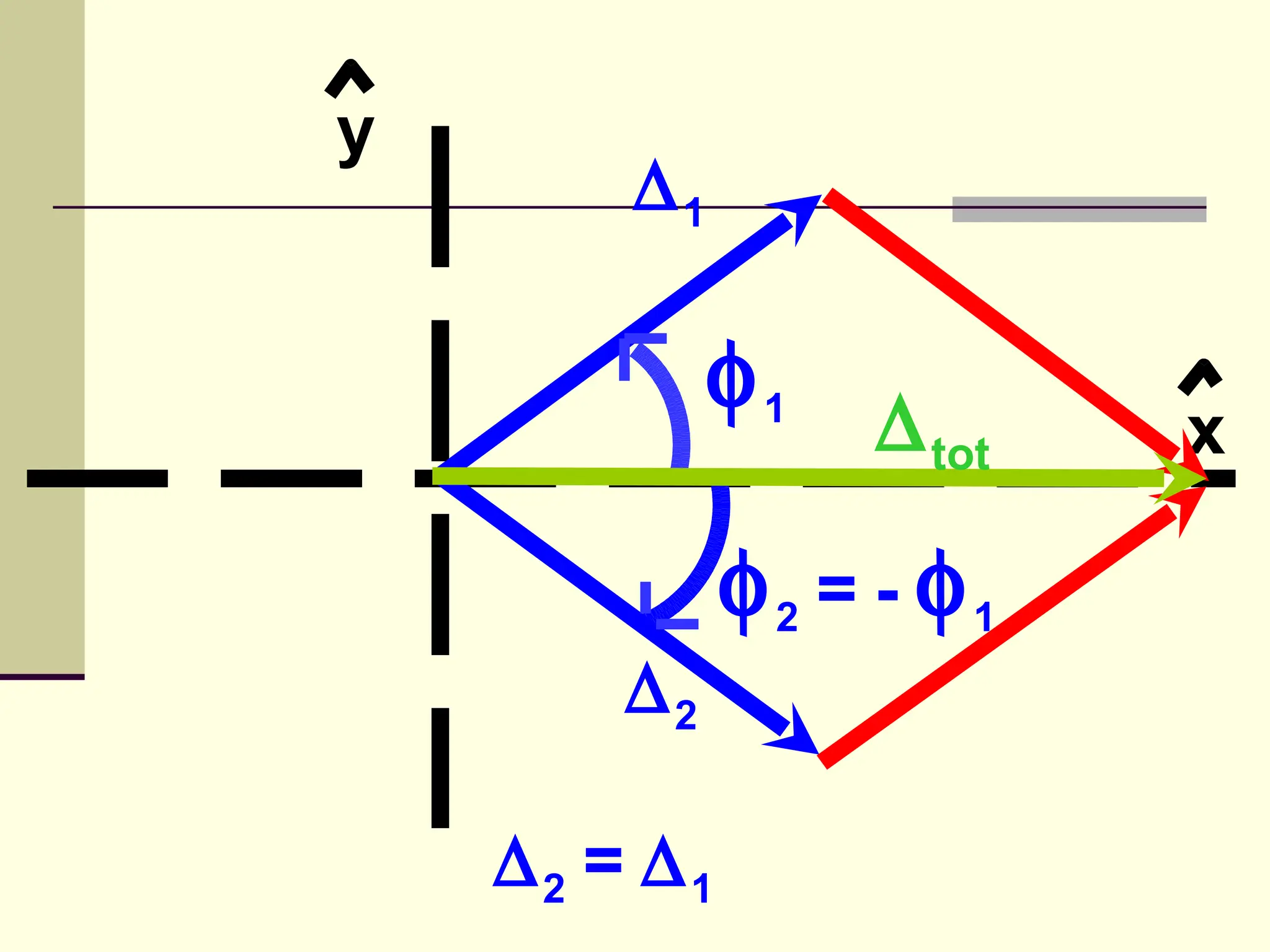
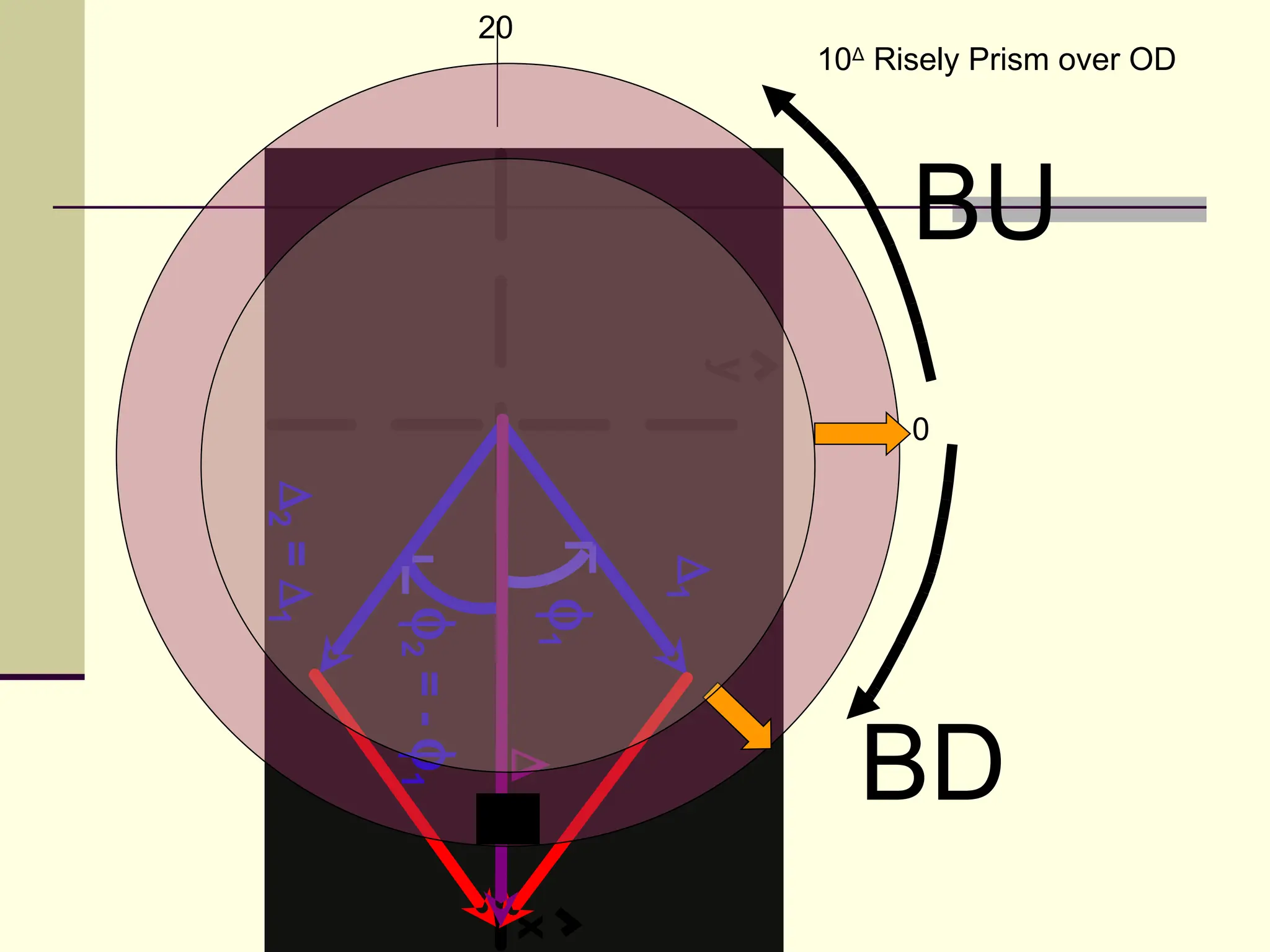
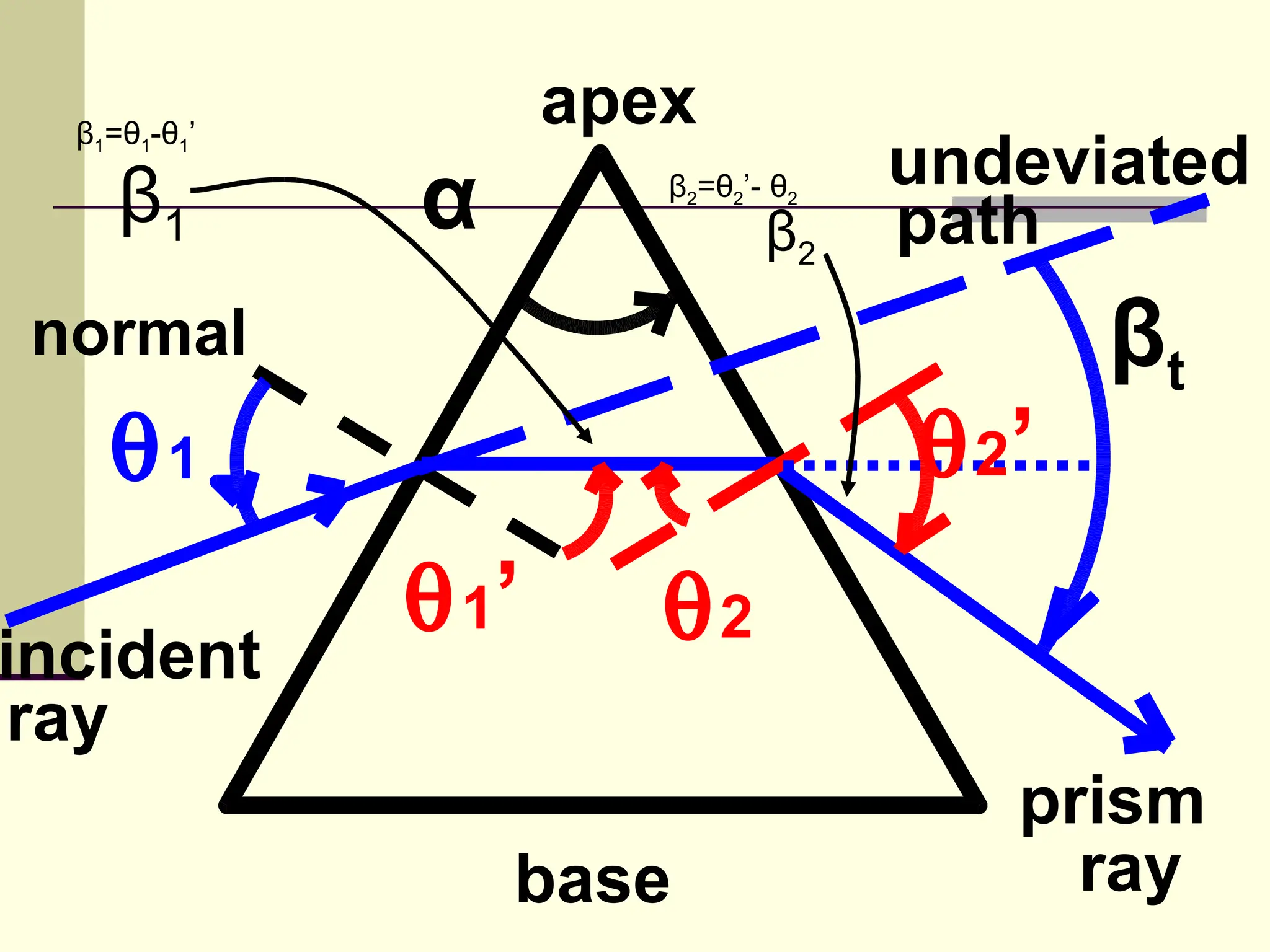
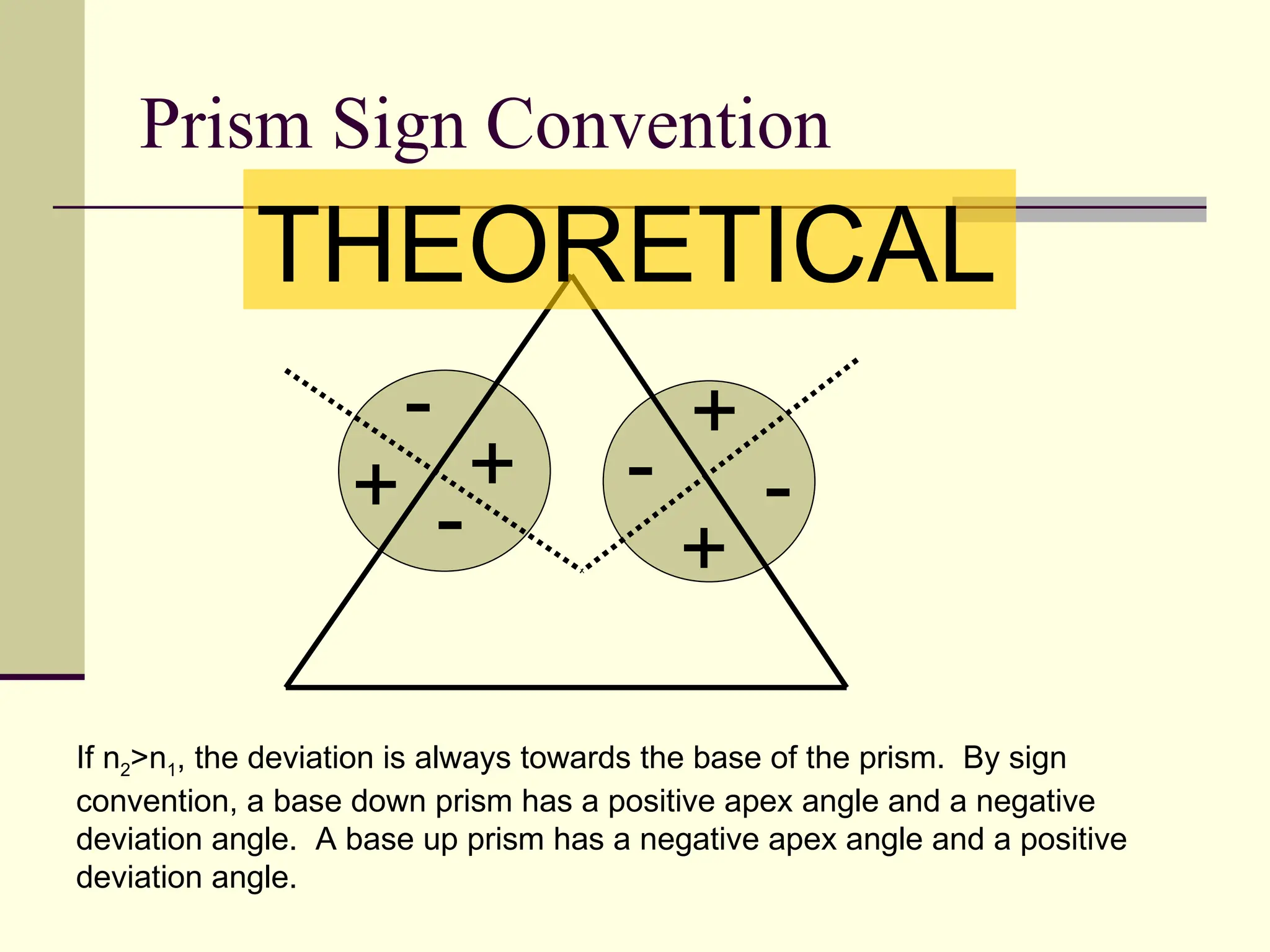
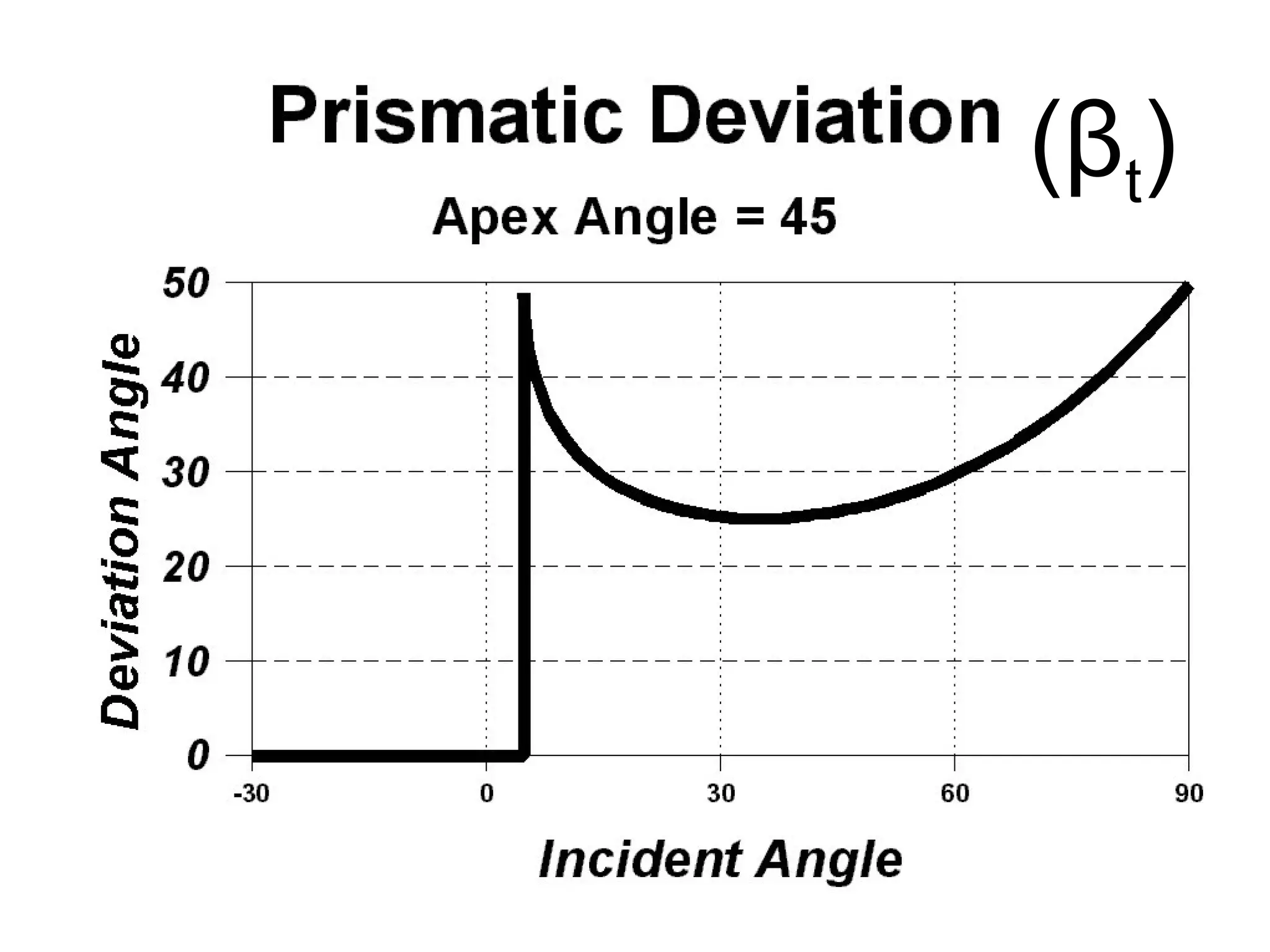
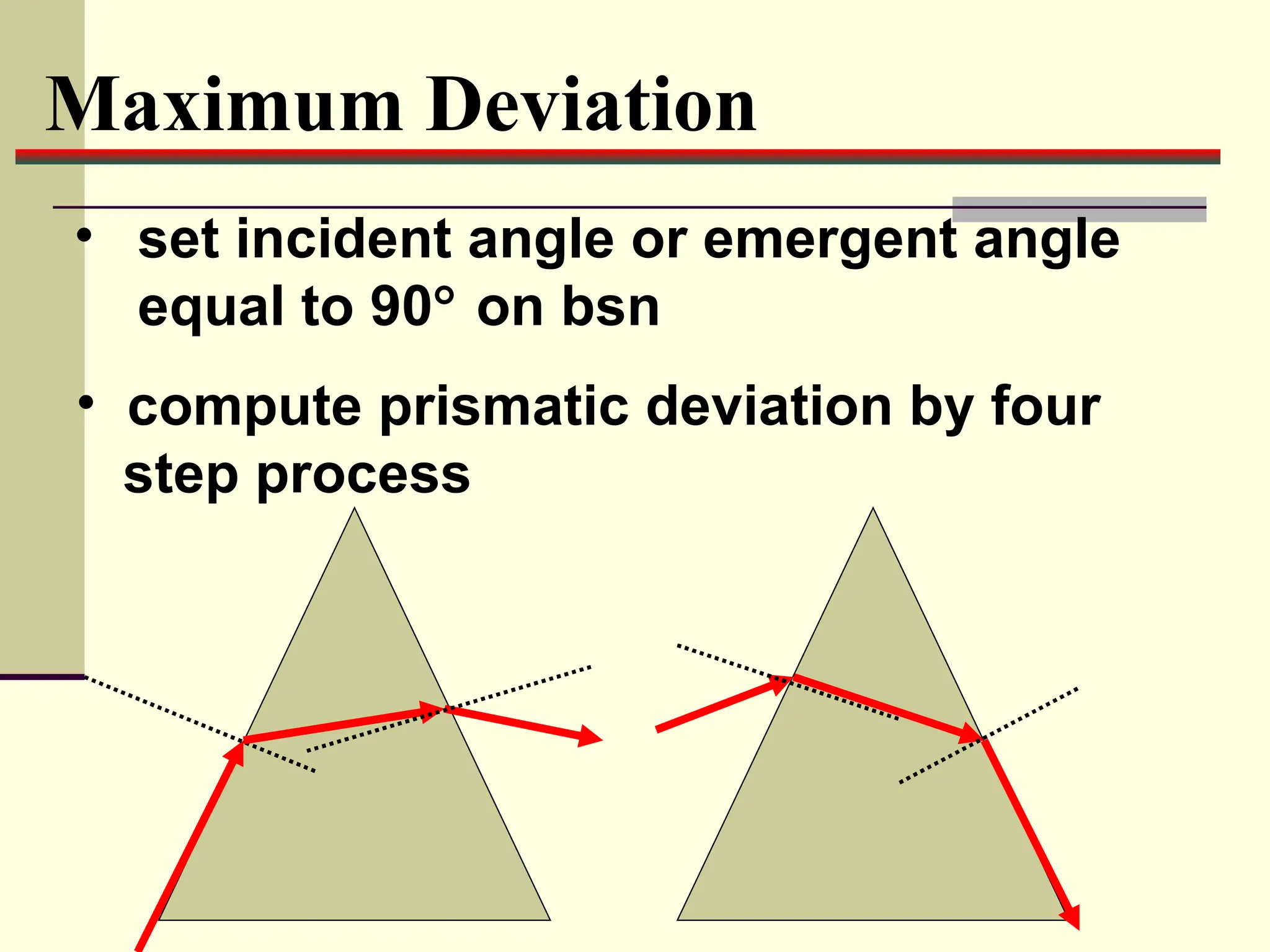
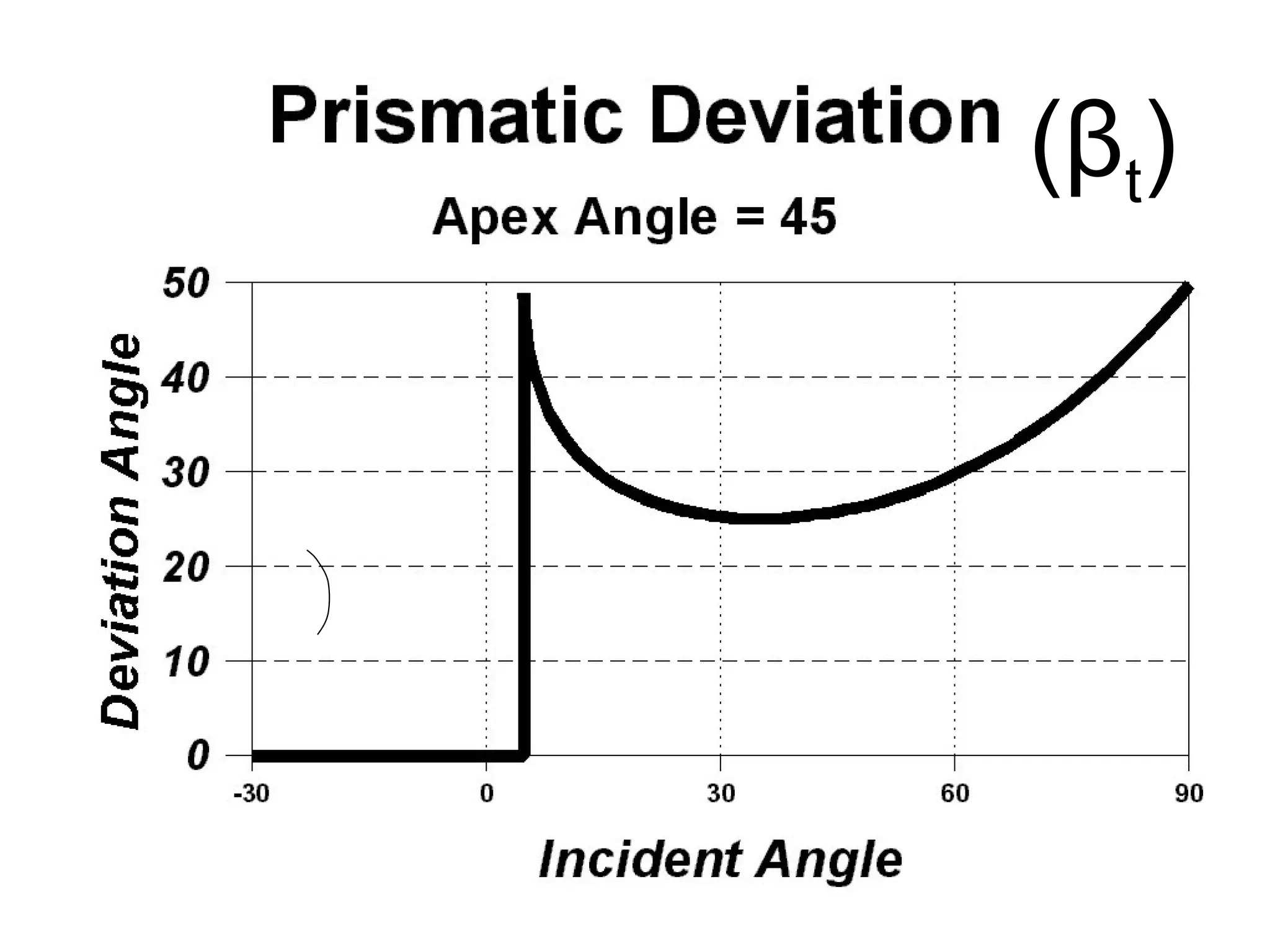
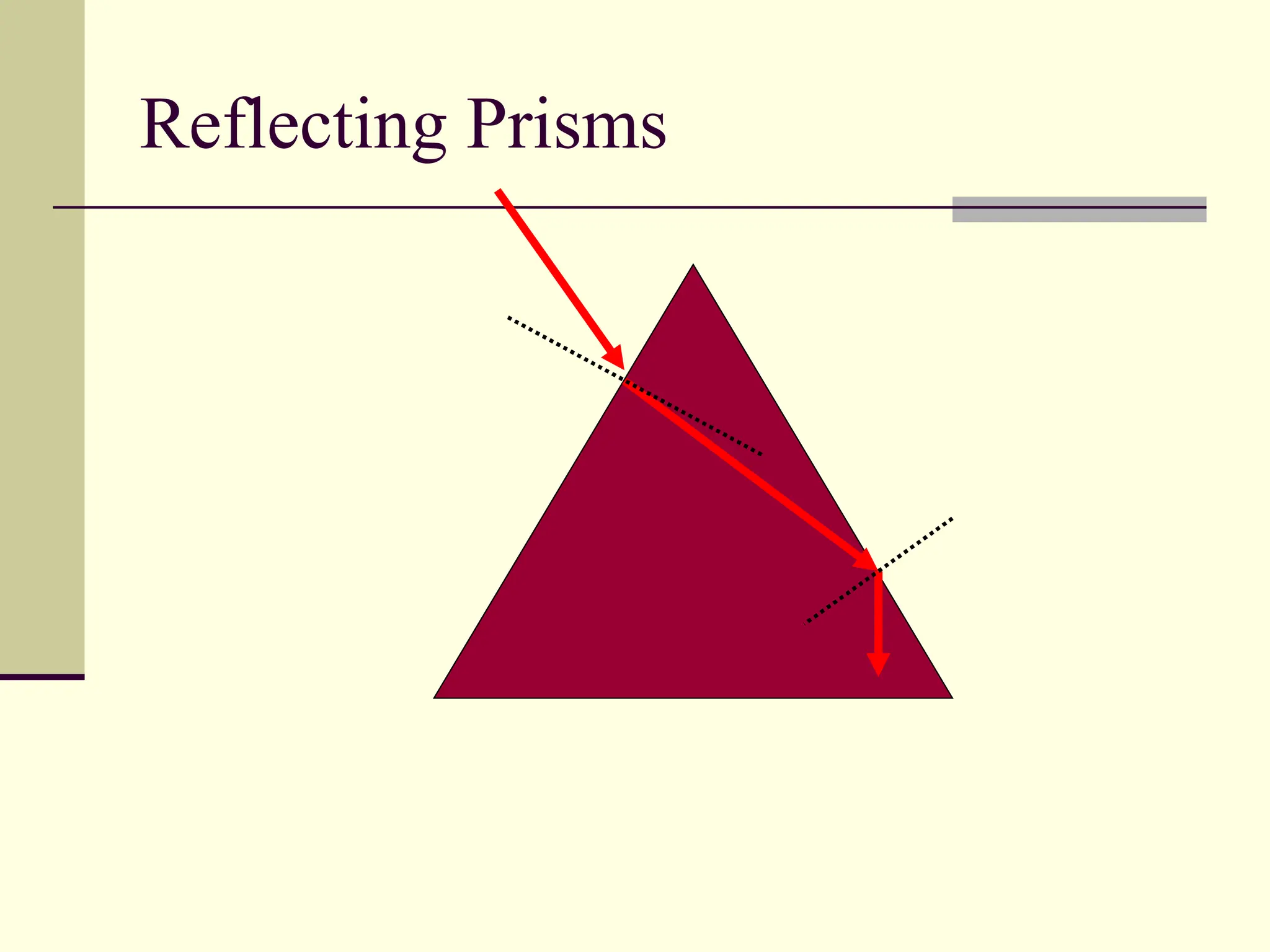
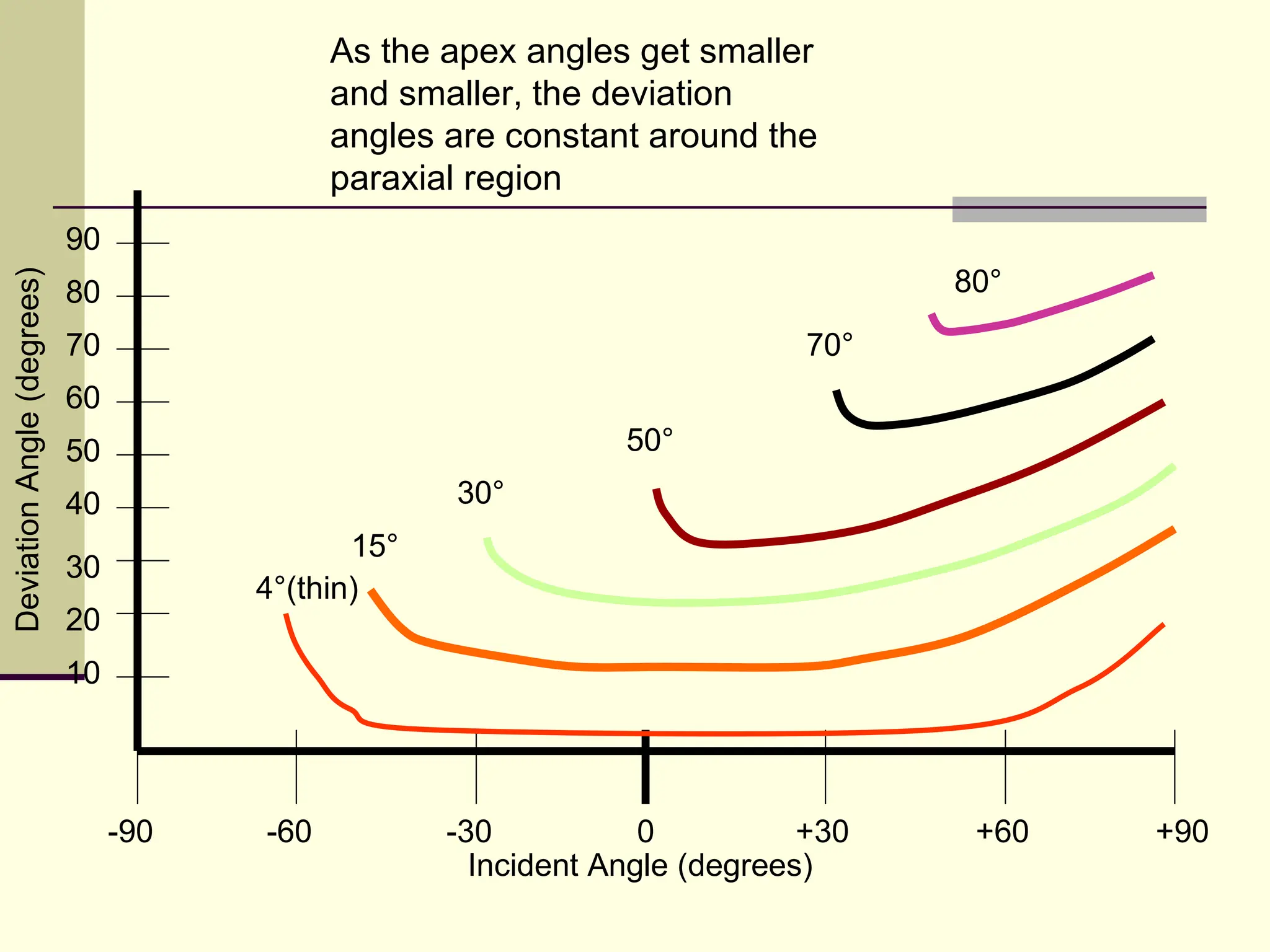
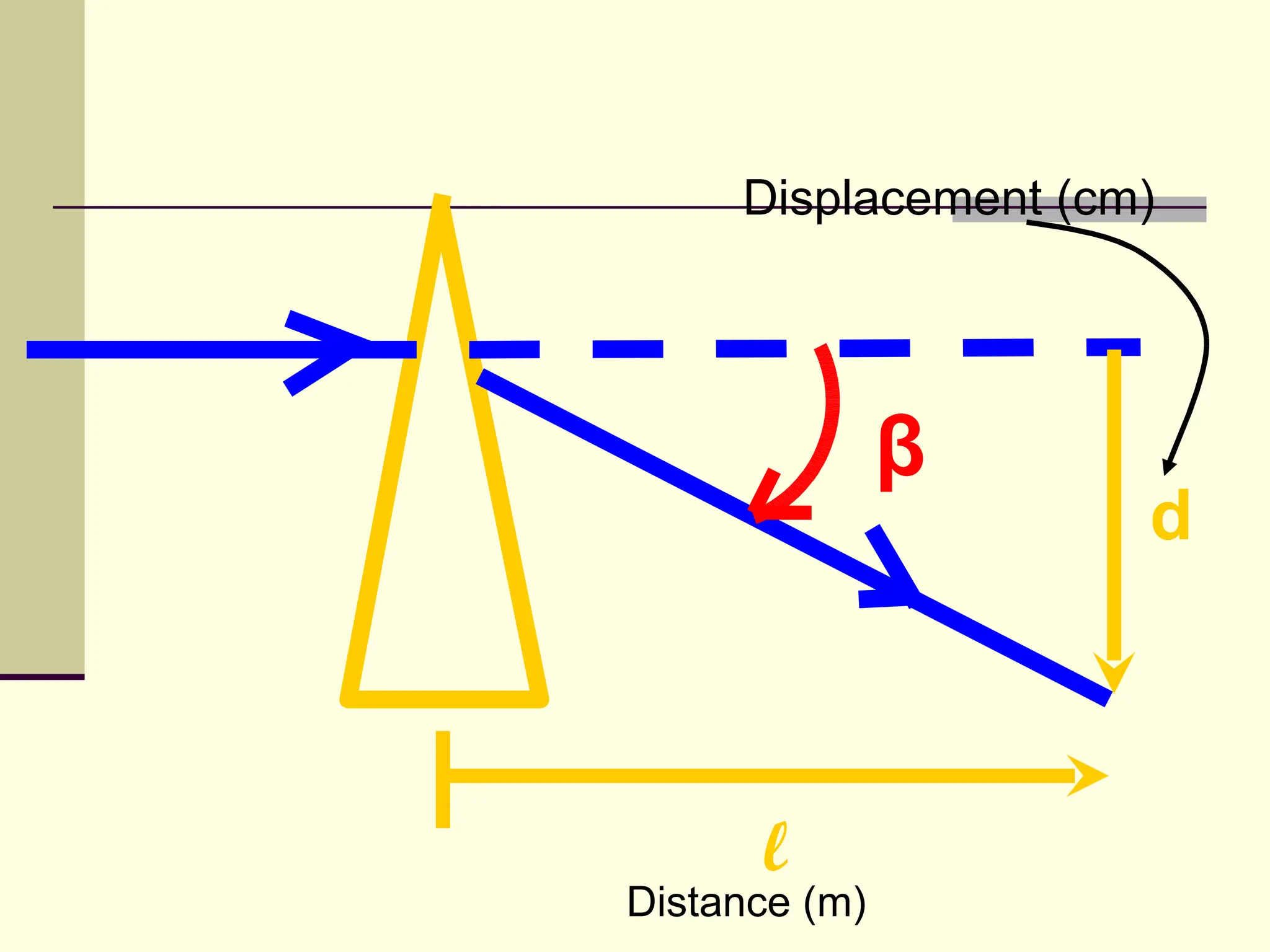
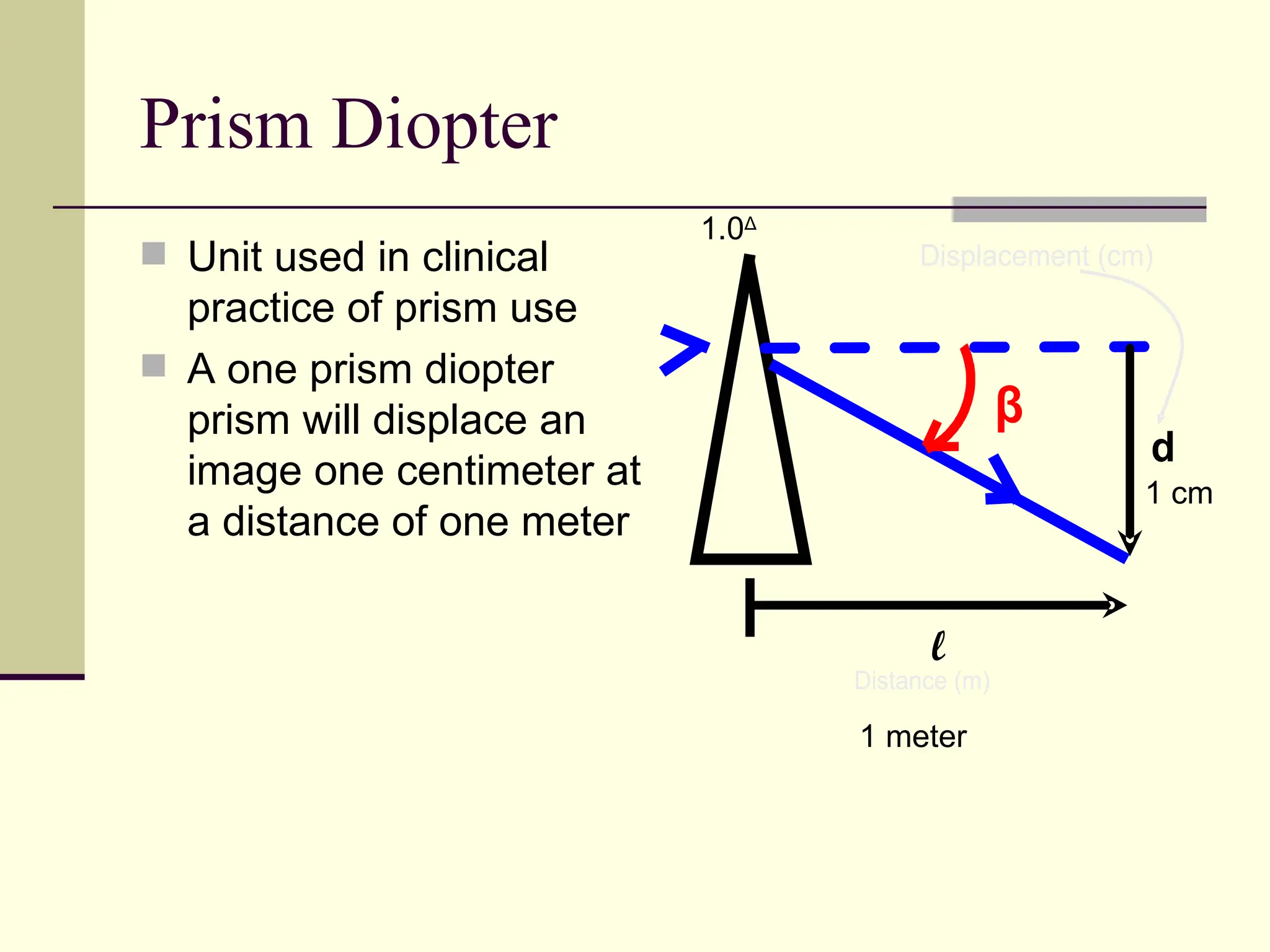
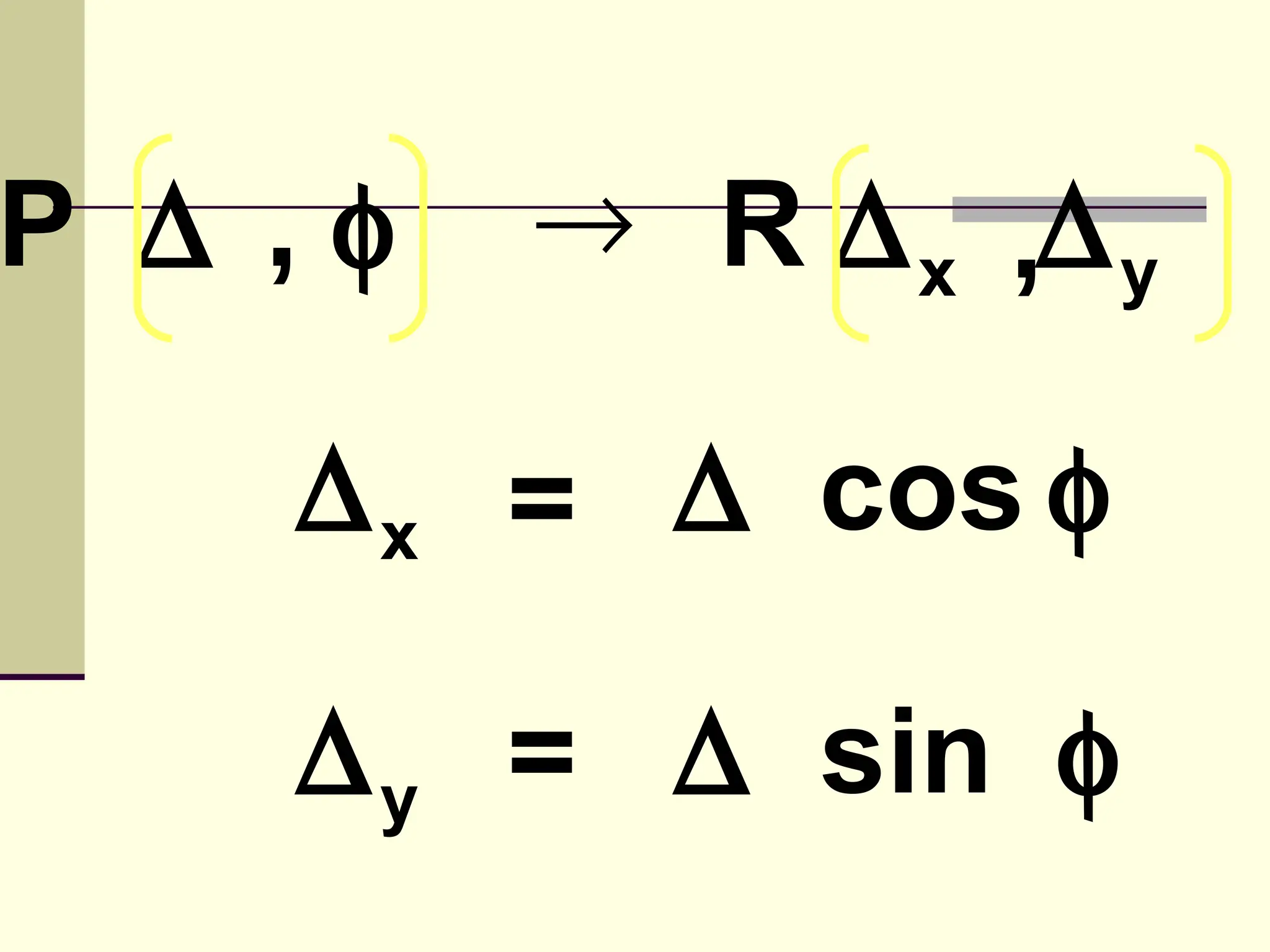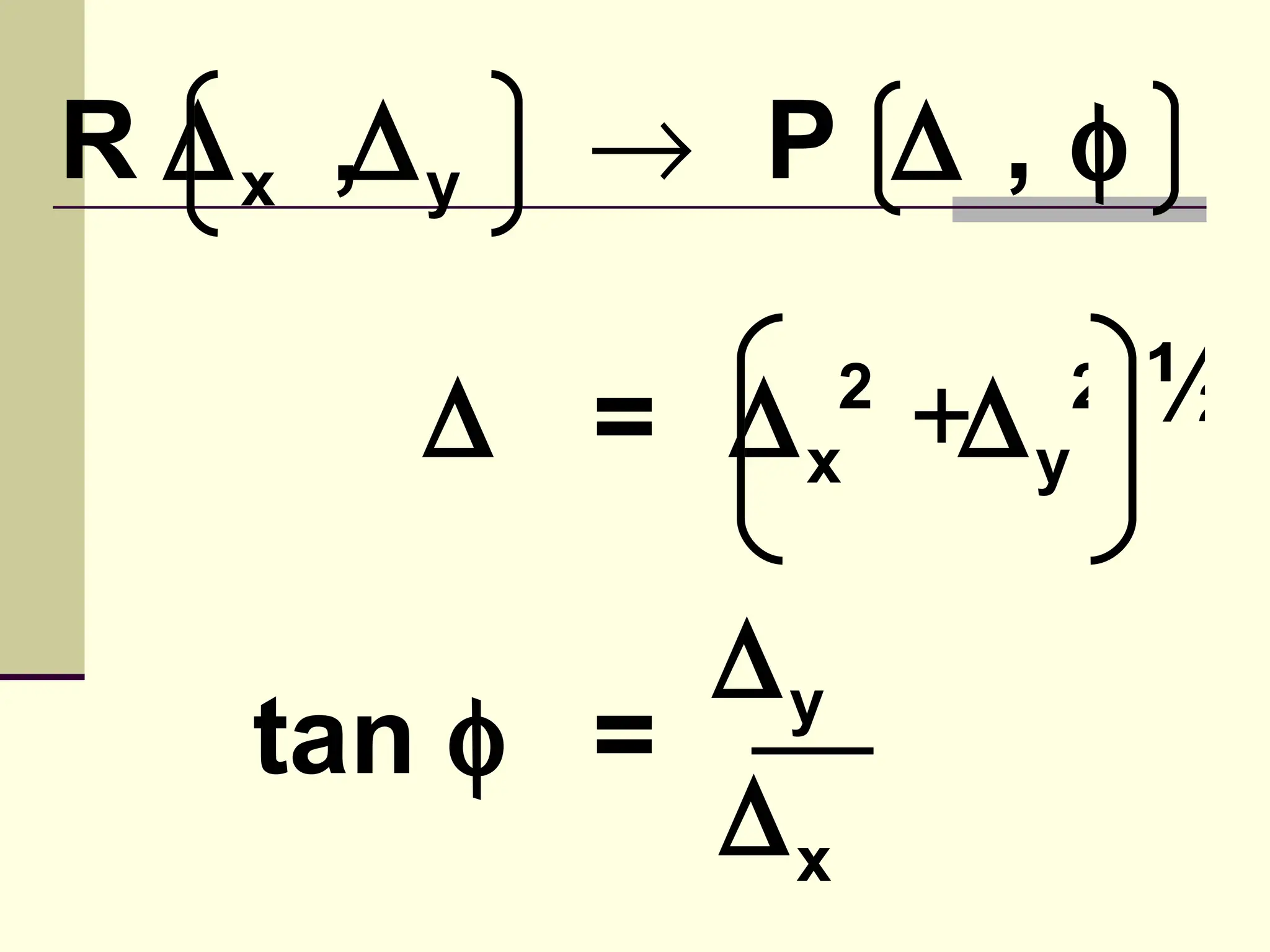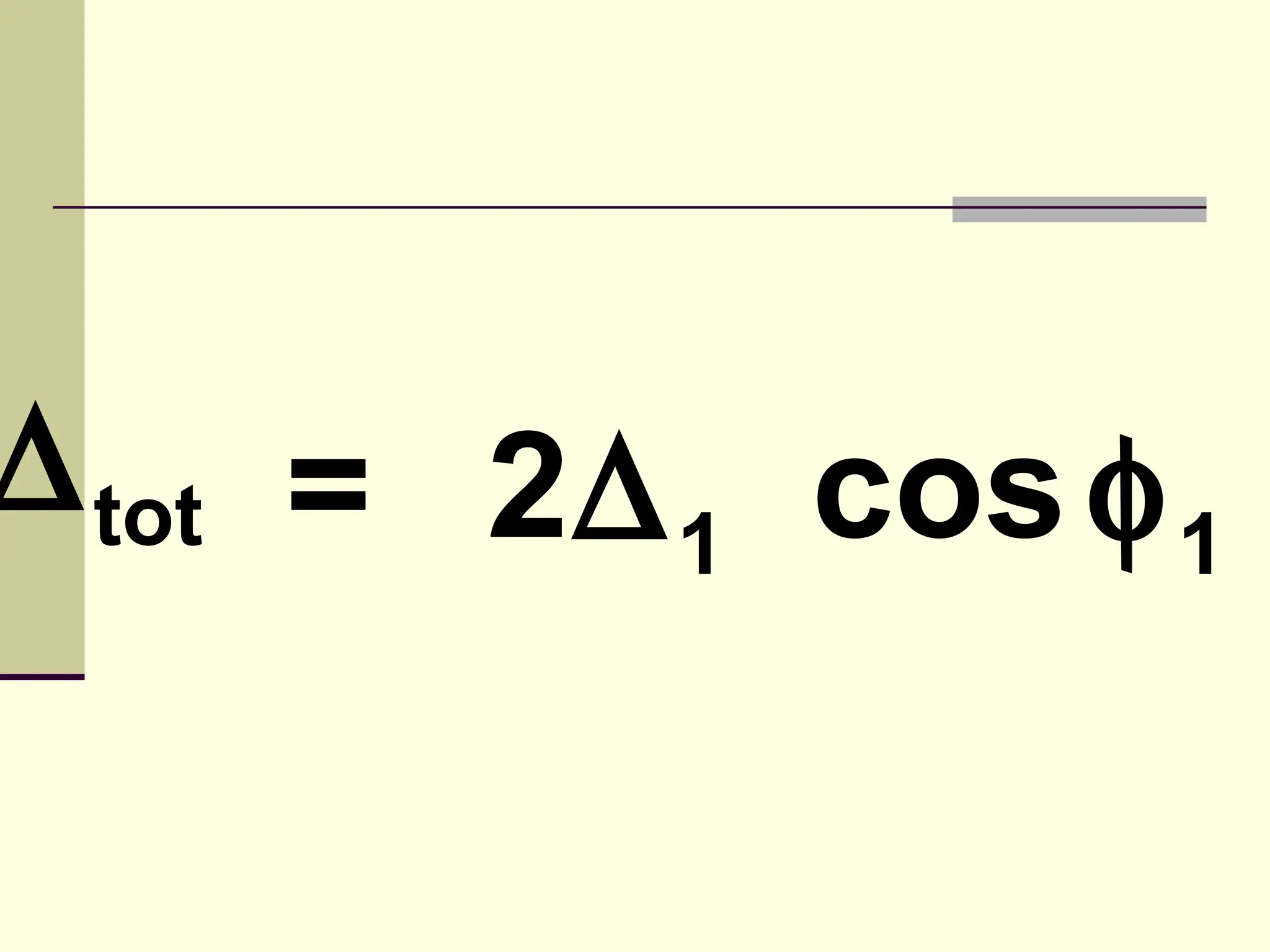This document defines and explains the properties of prisms, including their apical angle, deviation angle, minimum and maximum deviation, index of refraction determination using thick prisms, prism base directions in relation to a patient, and prism diopter units. It provides equations and examples to demonstrate how to calculate deviation angles, minimum and maximum deviations, index of refraction, and prism power in degrees and diopters.

1. Prisms and its properties
Gauri S. Shrestha, M.Optom, FIACLE

2. apex
undeviated
Refracting Surface
β
deviated
incident
base

3. Definitions
 Prisms: Two plane surfaces inclined at an angle
with respect to each other
 Refracting Surfaces: The two interfaces of
refraction in a prism. Inclined at an angle equal to
the apex angle.
 Reflecting Surface: In some prism setups, the
internal ray hits the second refracting surface such
that total internal reflection occurs (Reflecting
Prism)

4. Definitions
 Apical Angle (α): The angle between the two
refracting surfaces in a standard refracting prism.
Also referred to as the “Refracting Angle”.
 Apex: The tip of the prism where the two
refracting surfaces meet. The apical angle is the
apex of the prism
 Base: The bottom of the prism or the side
opposite the apex or apical angle. The orientation
of an ophthalmic prism is described relative to the
base

5. Deviation Angle
 The angle from the original light ray path
direction to the direction of the same light ray
after passing through the prism
 We will use the nomenclature of (β)

6. β1=θ1-θ1’
apex
undeviated
β1 α β2=θ2’- θ2
β2 path
normal βt
θ1 θ 2’
θ 1’ θ2
incident
ray
prism
base ray

7. n1 sin θ 1 = n2 sin 1’
θ
α = θ 1’ + θ 2
n2 sinθ 2 = n3 sinθ 2’
βt = β1 + β2
βt = θ 1 +θ 2’ - α

8. βT = β1 + β2
βT = (θ1 – θ1’) + (θ2’ – θ2)
β T + θ1 ’ + θ2 = θ2 ’ – θ2
β T + α = θ1 + θ2 ’
β T = θ1 + θ2 ’ - α

9. Prism Sign Convention
THEORETICAL
- +
+ -+ - -
+
If n2>n1, the deviation is always towards the base of the prism. By sign
convention, a base down prism has a positive apex angle and a negative
deviation angle. A base up prism has a negative apex angle and a positive
deviation angle.

10. A flint glass (n=1.617) prism in air has a 50 degree apex angle. What is the
deviation for a ray with an incident angle of 70 degrees on the base side of
normal?
Solution:
1
1.00 sin (70) = 1.617 sin θ1’
θ1’ = 35.53 degrees Note: This prism bends this
ray 43.83 degrees toward
2
α = θ1’ + θ2, 50 = 35.53 + θ2 ,
the base. By reversibility, a
θ2 = 14.47 degrees ray with an incident angle of
23.83 degrees will have a 70
3
1.617 sin (14.47) = 1.00 sin θ2’
θ2’ = 23.83 degrees
degree final angle of
refraction and 43.83 degree
β = θ1 + θ2’ - α deviation angle
4 β = 70 + 23.83 – 50
β = 43.83 degrees

11. Minimum Deviation
• internal ray perpendicular to bisector
of apex angle
• incident and emergent angles equal in
magnitude (θ1 = θ2’)
θ1
θ2’
βmin

12. (βt)

13. (α + min)
β
n2 sin
= 2
n1 α
Note that βmin is sin
dependent on only the 2
apical angle and the
indexes of refraction

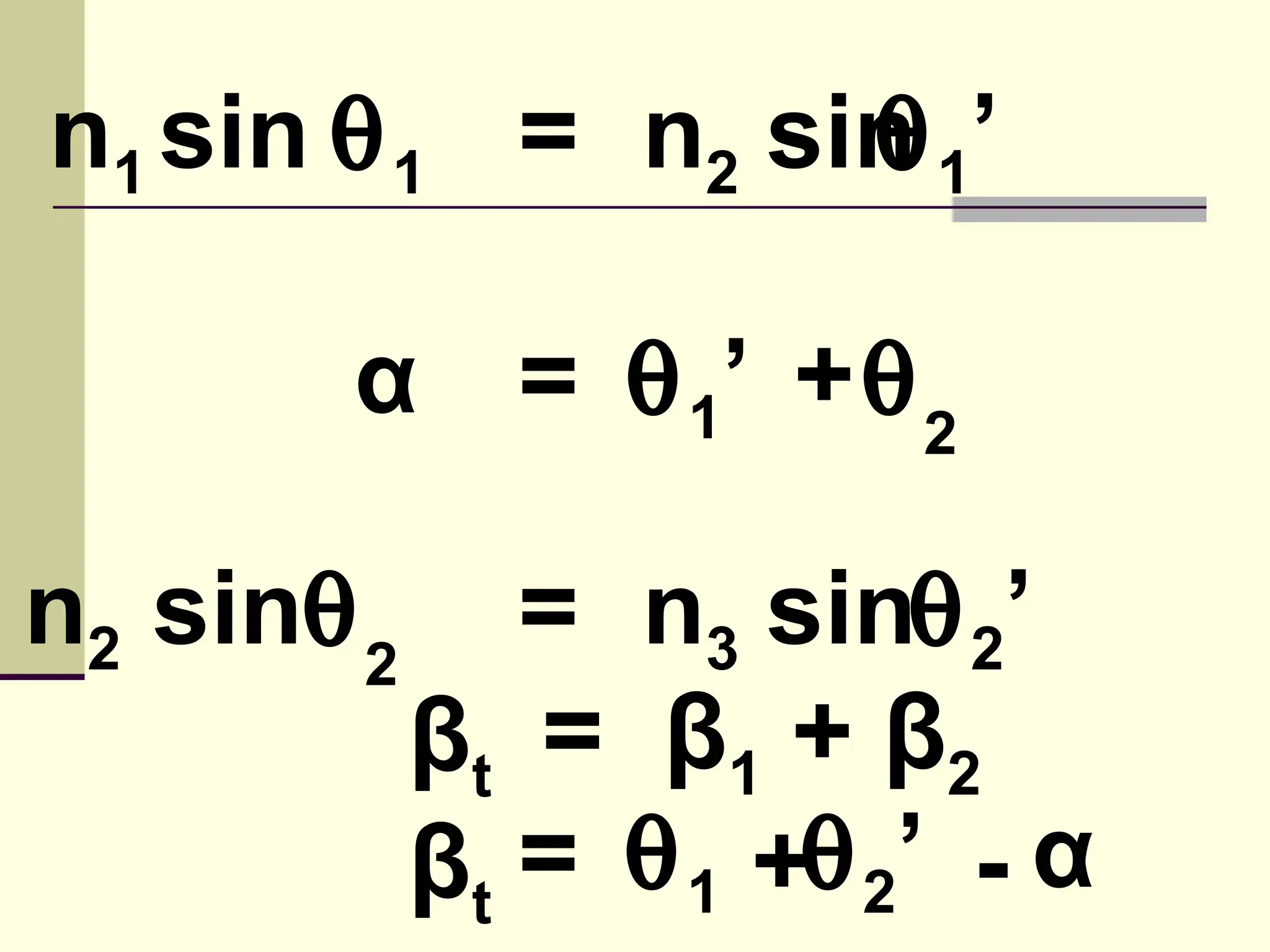
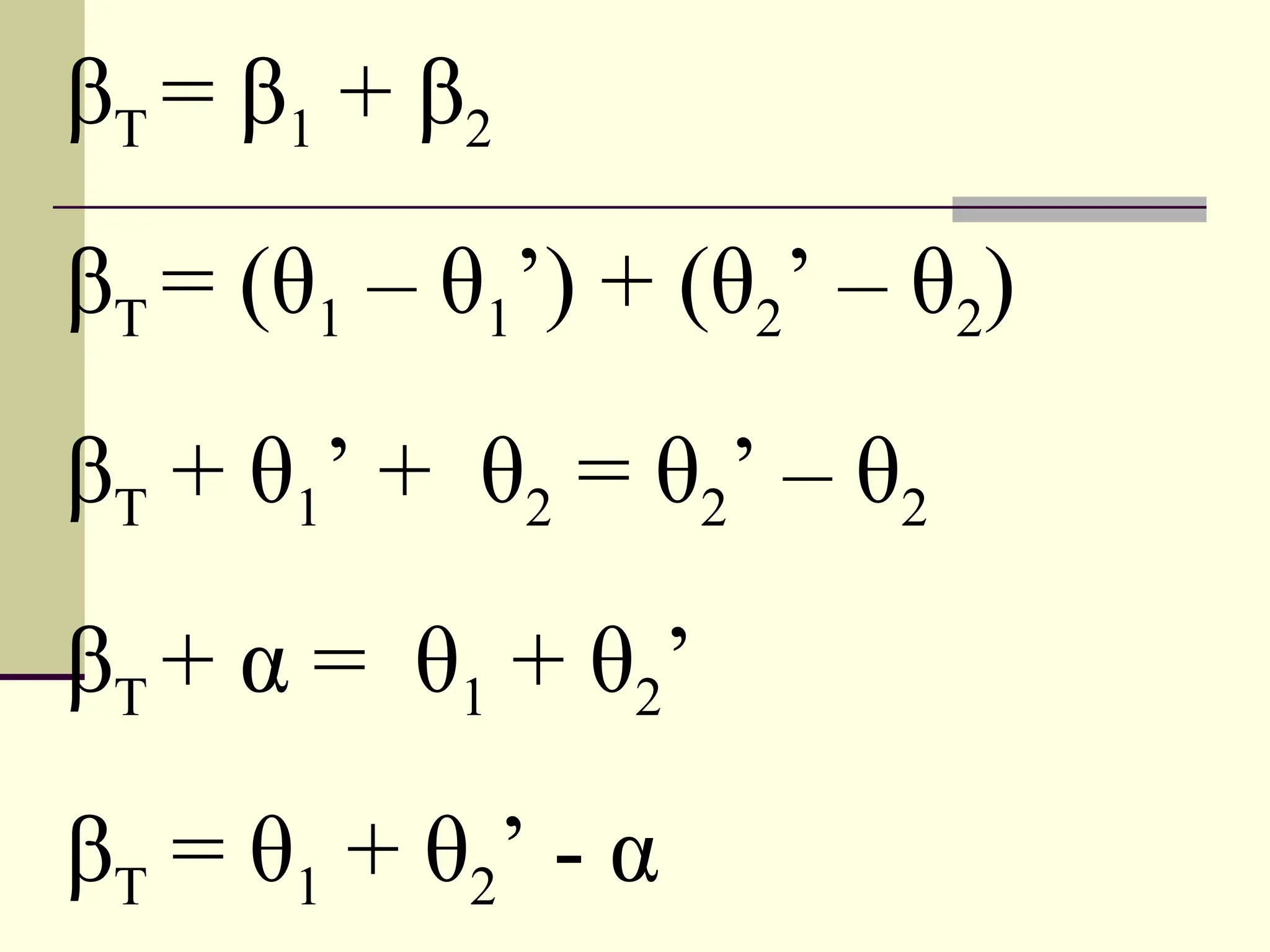
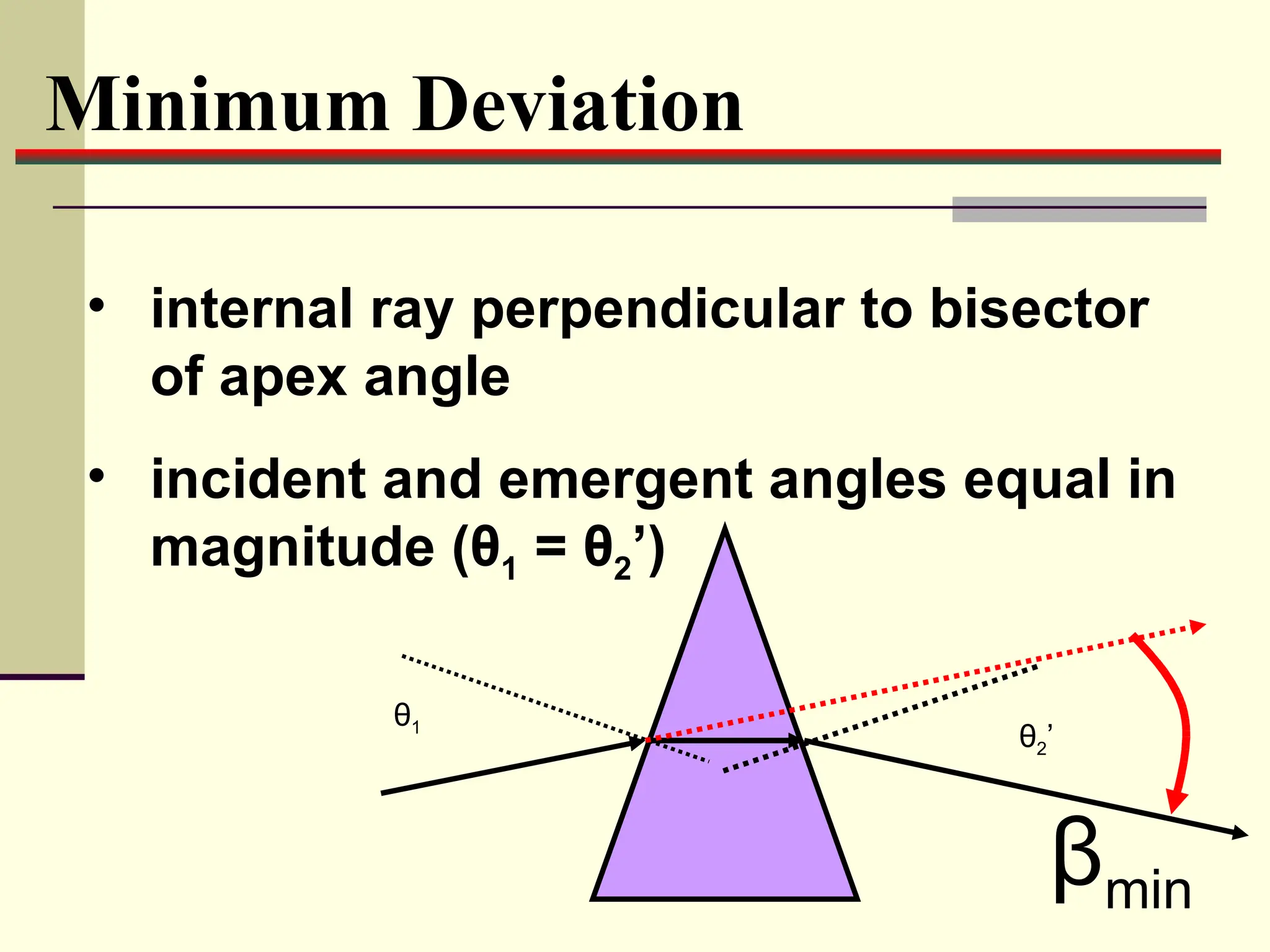
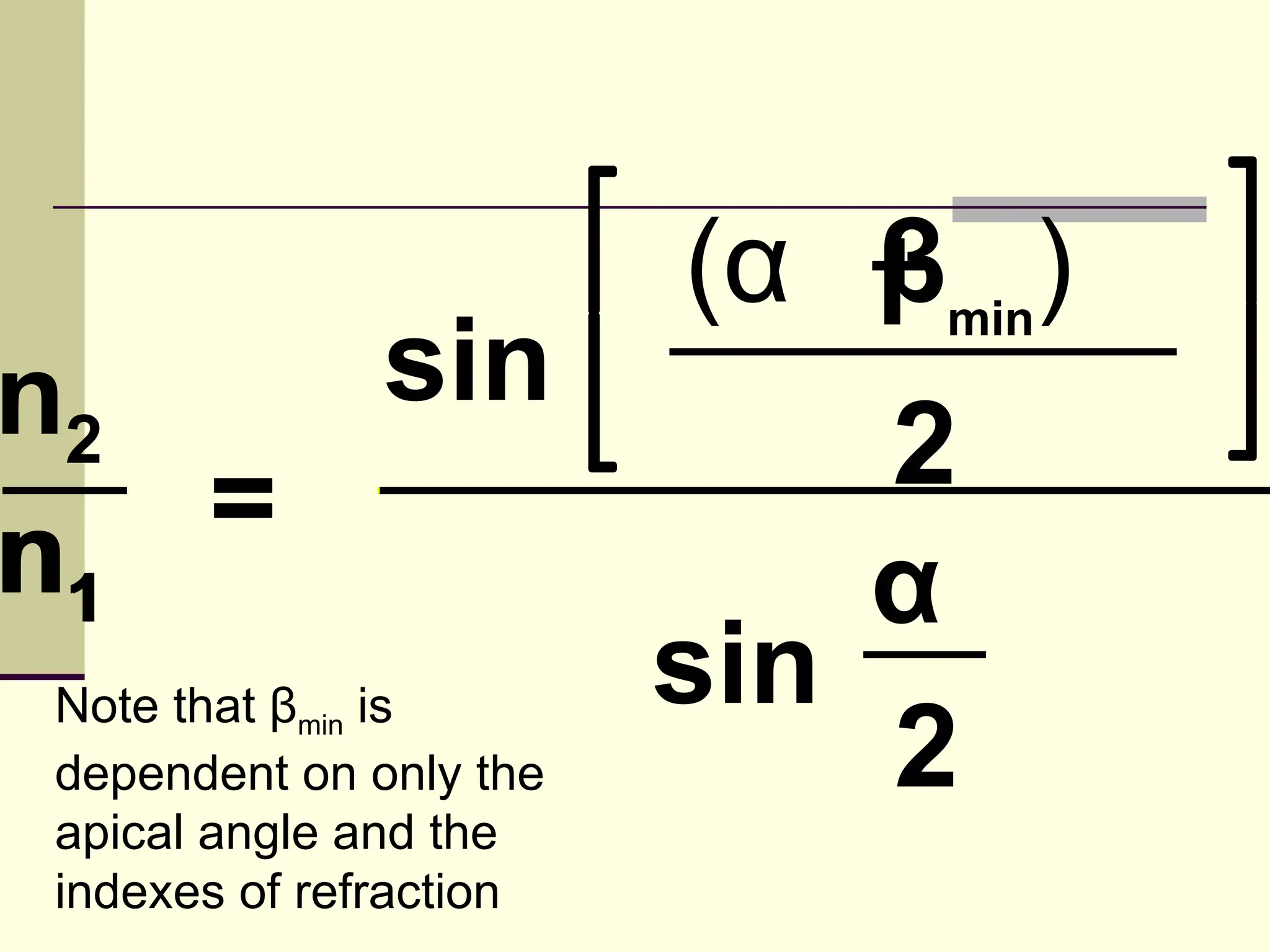
14. What is the minimum deviation through a flint glass prism (n
= 1.617) with an apical angle of 50 degrees
n2/n1 = sin [(α + βmin)/2]
sin (α/2)
1.617/1.00 x sin 25 = sin [(50 + βmin)/2]
βmin = 36.2 degrees

15. Maximum Deviation
• set incident angle or emergent angle
equal to 90° on bsn
• compute prismatic deviation by four
step process

16. What is the deviation angle for a ray that has grazing incidence on the base side
of the normal? (θ1=90 degrees) (MAXIMUM DEVIATION!) Assume the same
flint glass prism (n=1.617) with an apical angle of 50 degrees
Solution:
1.00 sin (90) = 1.617 sin θ1’ Note: Since grazing
1 θ1’ = 38.20 degrees
inicidence gives the largest
incident angle possible, the
α = θ1’ + θ2 59.31 degree deviation is the
2 50 = 38.20 + θ2
θ2 = 11.80 degrees
MAXIMUM DEVIATION that
this prism gives. By
reversibility, the 59.31 degree
maximum deviation will also
3
1.617 sin (11.80) = 1.00 sin θ2’
occur for an incident angle of
θ2’ = 19.31 degrees
19.31 degrees
4 β = θ1 + θ2’ - α
β = 90 + 19.31 - 50
β = 59.31 degrees

17. (βt)

18. Limitations of Refraction Through
Prism
 Light will not be refracted through a prism if the
internal angle at the second refracting surface is
greater than the critical angle
 What incident angle at the first surface of the prism
will yield the critical angle at the second refracting
surface?
 Solve for critical angle and work backwards to find
the limiting incident angle
 Incident angles less than this will not be refracted
through the prism and will undergo TIR

19. Reflecting Prisms
 Created by an angle of incidence which after
refracting through the first surface of the
prism is incident on the second surface at an
angle creating total internal reflection at the
second surface
 Can be a positive or negative incident angle,
depending on the apical angle and the index
of refraction

20. Reflecting Prisms

21. For the same prism (n = 1.617, apical angle = 50 degrees), what is the deviation
angle for an incident angle of 10 degrees on the base side of the normal?
Solution:
1.00 sin (10) = 1.617 sin θ1’
1 θ1’ = 6.17 degrees
α = θ1’ + θ2
2 50 = 6.17 + θ2
θ2 = 43.83 degrees
3
1.617 sin (43.84) = 1.00 sin θ2’
sinθ2’ = 1.12 θ2’ = Error (The sin function cannot be greater than zero)
4 Total Internal Reflection

22. (βt)

23. Prism Deviation and Apex Angles
 The largest deviation possible through a
prism would be the condition where:
 θ1= θ’2 = 90°
α = θ’1 + θ2 `=θc + θc
 θ’1 = θ2 = θc α = 2θc
If the apex angle is greater
than two times the critical
angle, no incident rays will be
refracted through the prism
This demonstrates that an apex angle greater than two
times the critical angle creates TIR at the second surface
no matter the incident angle

24. What is the maximum apex angle that a prism (n=1.50) can have so that the
prism can still refract incident light through without TIR?
sin θc = n’/n
sin θc = 1.00/1.50
θc = 41.81 degrees
α(max) = 2(41.81)
= 83.62 degrees

25. Determining Index of Refraction
Using Thick Prisms
 Spectrometer can be used to narrow the
wavelength of light to minimize chromatic
aberrations.
 Dmin can be determined

26. (α + min)
β
n2 sin
= 2
n1 α
Note that in air, the index of sin
the prism can be determined
by knowing the apex angle
and the minimum angle of
2
deviation

27. A 48 degree prism has a minimum deviation of 27
degrees. What is the index of refraction of the material
which makes up this prism?
n2 = sin [ (α + βmin) / 2 ]
sin (α / 2)
n2 = sin [ ( 48 + 27) / 2 ]
sin (48 / 2)
n2 = 1.50

28. As the apex angles get smaller
and smaller, the deviation
angles are constant around the
paraxial region
90
80°
Deviation Angle (degrees)
80
70 70°
60
50 50°
40 30°
15°
30
4°(thin)
20
10
-90 -60 -30 0 +30 +60 +90
Incident Angle (degrees)

29. Thin Prisms
 Have a clinically constant deviation angle in
the paraxial area (± 20 °)
 Don’t have to worry about where a patient is
looking through the prism
 Defined as prisms with an apical angle of less
than 8°-15°
 Defined as prisms with a prismatic power of
approximately 15 to 25 or less
Δ Δ

30. Deviation by Thin Prisms
np
β = (n )α
-1
s

31. What is the deviation angle of an 8 degree apical angle prism
(n=1.49) in water? In air?
QUESTION: Do you predict the deviation to be greater in Water or Air?
Solution: (in water)
β = [(np/ns) – 1] α
β = [(1.49/1.33) -1] 8
β = 0.96°
(in air)
β = [(np/ns) – 1] α
β = [(1.49/1.00) -1] 8
β = 3.92°

32. Prism Diopter Unit

33. Displacement (cm)
β
d
l
Distance (m)

34. d in cm
∆ =
l in m
= 100tanβ

35. Prism Diopter
1.0Δ
 Unit used in clinical Displacement (cm)
practice of prism use
 A one prism diopter
prism will displace an β
d
image one centimeter at 1 cm
a distance of one meter
l
Distance (m)
1 meter

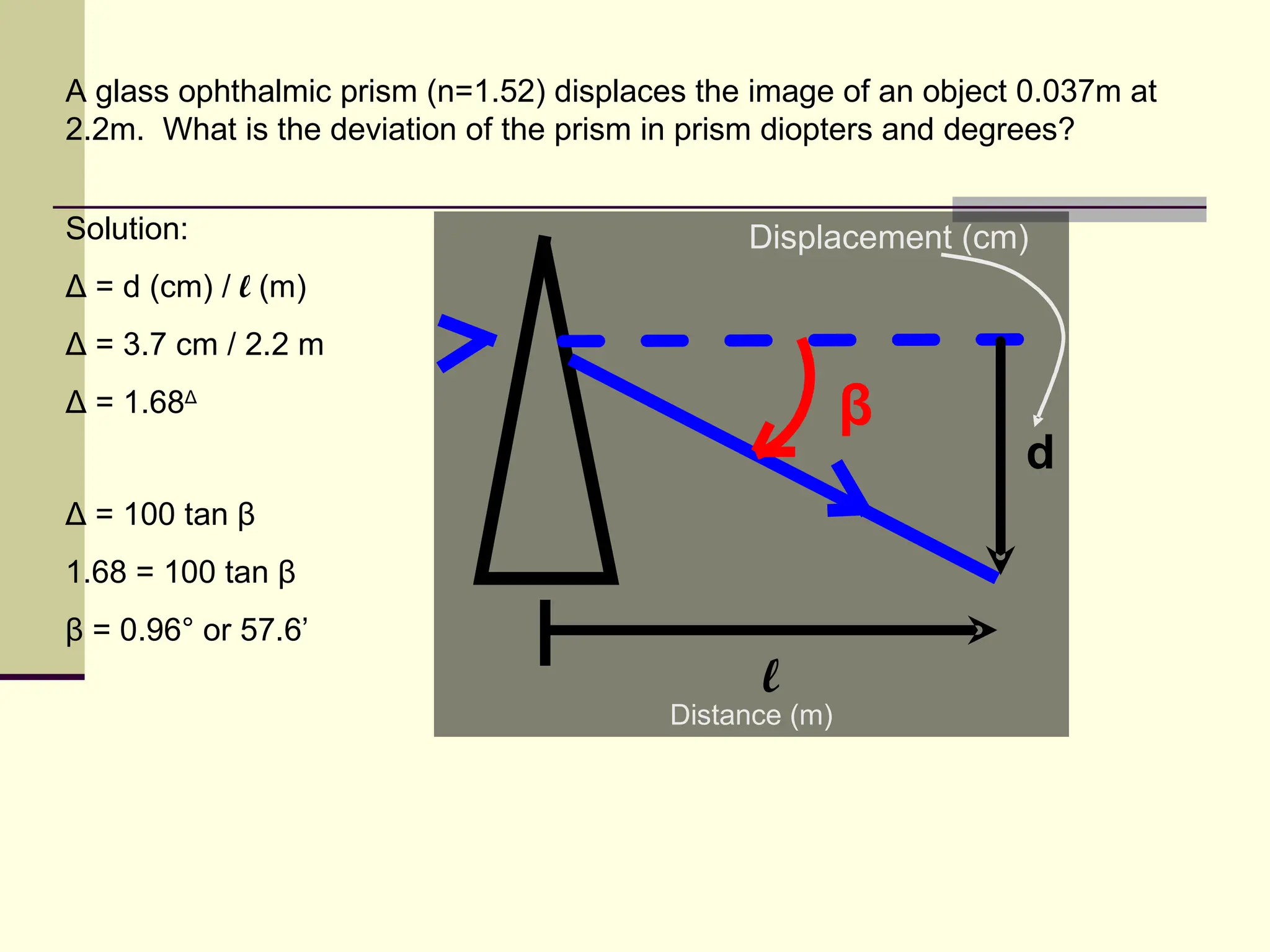
36. What is the deviation angle of an 8 degree apical angle prism
(n=1.49) in water? In air? Give the answer in terms of prism
diopters.
Solution: (in water)
β = [(np/ns) – 1] α
β = [(1.49/1.33) -1] 8
β = 0.96° Δ = 100 tan β = 1.68Δ
(in air)
β = [(np/ns) – 1] α
β = [(1.49/1.00) -1] 8
Δ = 100 tan β = 6.85Δ
β = 3.92°

37. A glass ophthalmic prism (n=1.52) displaces the image of an object 0.037m at
2.2m. What is the deviation of the prism in prism diopters and degrees?
Solution: Displacement (cm)
Δ = d (cm) / l (m)
Δ = 3.7 cm / 2.2 m
Δ = 1.68Δ β
d
Δ = 100 tan β
1.68 = 100 tan β
β = 0.96° or 57.6’
l
Distance (m)

38. Prism Base Directions re
Patients

39. BU
Patient BU
OD OS
BO BI BI BO
BD BD

40. Patient
B@135 B@135
B@45 B@45
OD OS
B@225 B@315 B@225 B@315

41. Patient
90 90
135 45 135 45
180 OD 0 180
OS 0
225 315 225
315
270 270

42. QUIZ #2
 QUESTION #1
 A prism (n=1.60) deviates a light ray surrounded
by air ____________ it deviates the light ray
when the same prism is surrounded by water.
 A. more than
 B. less than
 C. the same as
 D. I don’t know. I was asleep in class today

43. QUIZ #2
 QUESTION #2
 What is the approximate
incident angle(s) that
yield the maximum
deviation for the prism
shown?
 A. 6°
 B. 32°
 C. 90°
 D. A and B
 E. A and C

44. QUIZ #2
 Question #3
 What is the amount of light that is reflected
from a water/air plane interface?
 A. 2%
 B. 3%
 C. 4%
 D. 7%
 E. 14%

45. QUIZ #2
 Question #4
 At plane refractive surfaces, a virtual object
produces which type of image?
 A. Virtual Image
 B. Real Image
 C. Virtual or Real image depending on the
vergence effect of the plane refractive
surface
 D. A virtual object CANNOT be incident on a
plane refractive surface!

46. Prism Image Displacement

47. β = Rotational
Stimulus
h
β
EYE
l
The image displacement, the eye’s
rotational stimulus, and the actual
rotation of the eye can be expressed
in either degrees or prism diopters. BD

48. QUESTION
 Does the prism have the same effect on the
eye when the prism is moved away from the
eye?
 Answer: NO
 If viewing a near object
 Answer: YES
 If viewing a distant object (at infinity)

49. β>βe
h Effective Displacement
β βe
EYE
l l’
BD

50. Prism Effectivity
 Effective Displacement = Eye Rotation Stimulus
 As a prism is moved away from the eye the ‘effect’
that it has on the eye decreases (assuming the image
is closer than infinity)
 The rotation stimulus decreases
 For a given prism power Δ (βΔ), the eye rotation
stimulus
 βΔe – Effective Displacement in Prism Diopters
 Can be defined by the following equation:

51. = h in cm = 100 tan βe
β Δ
e
l + l’ in m
β>βe
l ∆
=
l + l’
Effective Displacement
β βe
EYE
l l’
∆
=
1 + l’ As l increases, β = βe
BD
l l increases, β = βe
AsAs ldecreases, βe approaches zero

52. Prism Effectivity
variable object
0.9
0.85
0.8
0.75
0.7
25 30 35 40 45 50
object distance (cm)
10 cm 6 cm
Prism Distance

53. Prism Effectivity
 REMEMBER: If an object is at infinity, then
there is no effective change in prism power at
the eye no matter the distance the prism is
away from the eye

54. Prism Effectivity
variable prism distance
0.95
0.9
0.85
0.8
0.75
0.7
5 6 7 8 9 10 11 12 13 14 15
eye-prism distance (cm)
40 cm 50 cm
Object Distance

55. Prism Effectivity
 REMEMBER: If a prism is at the surface of
the eye (really the center of curvature), there
is no effective change in prism power at the
eye no matter the distance of the object.

56. Effectiveness of Prism
 Measured by relative eye rotation
 Visual Prism Demand (need) is the amount of prism
“effect” required by the eye to get desired result
(single, comfortable binocular vision)
 Therefore, if a patient if viewing a near object and a
prism is some distance in front of the eye
(spectacles), the eye is possibly not having its PRISM
DEMAND met.

57. What is the effectivity of a 15 prism diopter prism located 25mm in front of the
center of rotation of the eye, when the wearer reads at a distance of 40 cm from
the prism?
Solution:
βeΔ = 15 / 1 + (2.5/40)
βeΔ = 14.12Δ
Loss of approximately 1 prism diopter of effectivity

58. Prism Effectivity
 Since prisms are usually prescribed in powers
of no more than a few prism diopters, the loss
in effectivity for near vision, is usually
clinically insignificant.
 Exceptions:
 High prism amounts
 Prisms used in phoropters (Risley) are routinely
used to measure deviations of high prism
amounts
 Risley prisms have a longer vertex distance than
glasses since it sits in front of the lens

59. A 35 year old white male presents to your office with a complaint of double
vision at near. He wears glasses for his myopia and has been told that he
wears prisms in his glasses. What are you going to do?
Current glasses prescription: OD: -5.00-1.25 x 180 5Δ BD
OS: -4.50-1.00 x 180
You find that he needs an addition prism diopter prism at near to maintain clear,
single, and comfortable vision.
Visual need = 6Δ at near
What do his current glasses give him at distance and near (30cm and
vertex distance of 2cm)?
Distance = 5Δ, Near = βeΔ = 5 / 1 + (2.0/30)
βeΔ = 4.7Δ

60. A 35 year old white male presents to your office with a complaint of double
vision at near. He wears glasses for his myopia and has been told that he
wears prisms in his glasses. What are you going to do?
What prism power would yield 6Δ at the working distance and vertex
distance provided?
βΔe = Δ / 1 + l’/l
6 = Δ / 1 + 2/30
Δ = 6.4Δ BD OD
What if 6.4Δ is too much prism for distance??? Now what?
SLAB-OFF PRISM or REVERSE SLAB-OFF PRISM: A way to
incorporate different amounts of vertical prism between distance and near

61. Prism Resolution

62. y ∆
φ
x

63. y ∆
∆y
φ
x
∆x

64. P ∆ ,φ → R ∆ x ,∆ y
∆ x = ∆ cos φ
∆ y = ∆ sin φ

65. R ∆ x ,∆ y → P ∆ ,φ
∆ = ∆ x
2
+∆ y ½
2
∆y
tan φ =
∆x

66. Prism Addition

67. Method 1
 complete the parallelogram
 total vector is arrow from origin to intersection
point

69. Method 2
 move end of one vector to tip of other vector
 total vector is arrow from origin to tip of moved
vector

70. ∆ y2
∆ ytot
∆ y1
∆ x1 ∆ x2
∆ xtot

71. Find the single prism equivalent to a 2Δ BI combined with a 5Δ BU in front of the
left eye.
5.4Δ@112
5
Patient
90 90
135 45 135 45
180 OD 0 180
OS 0
225 315 225
315
270 270
2
21.8
5
Solution: Using Formula –
tan Φ = Δy/Δx
Φ Δ2 = Δx2 + Δy2
Φ = tan-1 5/2
2 = 4 + 25
Φ = 68.2°
Δ = 5.39Δ

72. Adding Prisms Applied to an Eye
 Adding prisms in opposite base directions is
subtractive
 Adding prisms in same base directions is
additive

73. Clinical Application
 Prism Prescribing and
Analyzing
 Lensometry
 Ophthalmic Optics and
Opticianry

74. Risley Prism
 A pair of counter-rotating prisms
 Base direction stays constant but the magnitude
of the prism changes
 Can be rotated to set the base direction
 Found on all phoropters
 Used extensively in optometry

76. y
∆1
φ1 ∆
tot x
φ2 = - φ1
∆2
∆2 = ∆1

77. ∆ tot = 2∆ 1 cos φ 1

78. Each component of a Risley Prism is a 10Δ prism. The Risley is set so that both
prisms are BD. What is the maximum prism power? What is the power when
they are counter-rotated by 45° from the maximum.
Solution:
Maximum = 2 x 10 = 20Δ
Δ = 2 Δ1 cos Φ1
Δ = 2 (10) cos 45
Δ = 14.1Δ BD

79. 0
BO BI
10Δ Risely Prism over OD
y
∆1
φ1
20
∆ x
20
φ2 = - φ1
∆2 = ∆1

80. 20
10Δ Risely Prism over OD
BU
y
0
∆2 = ∆1
∆1
φ
φ2 = - φ1
1
BD
∆
20
x