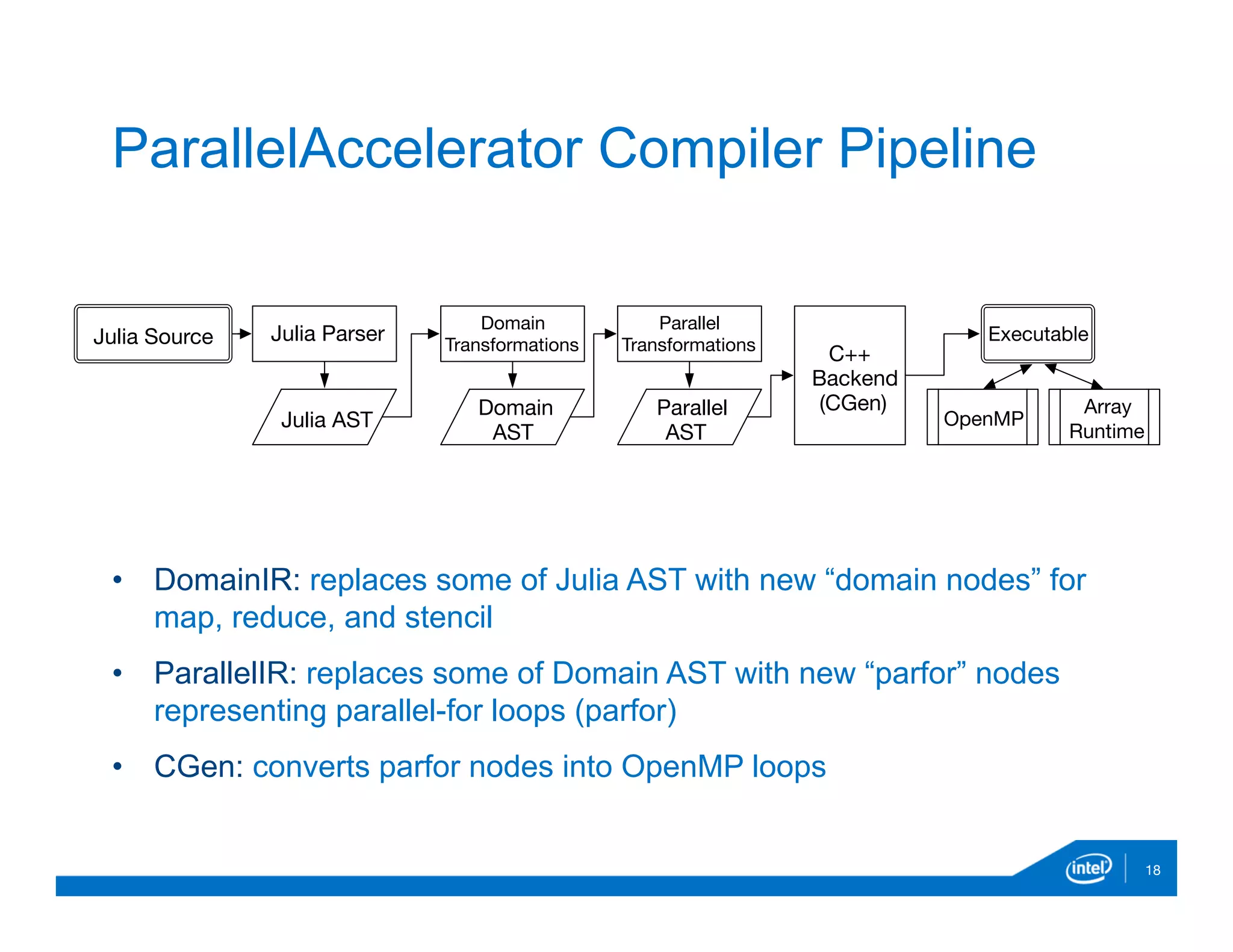
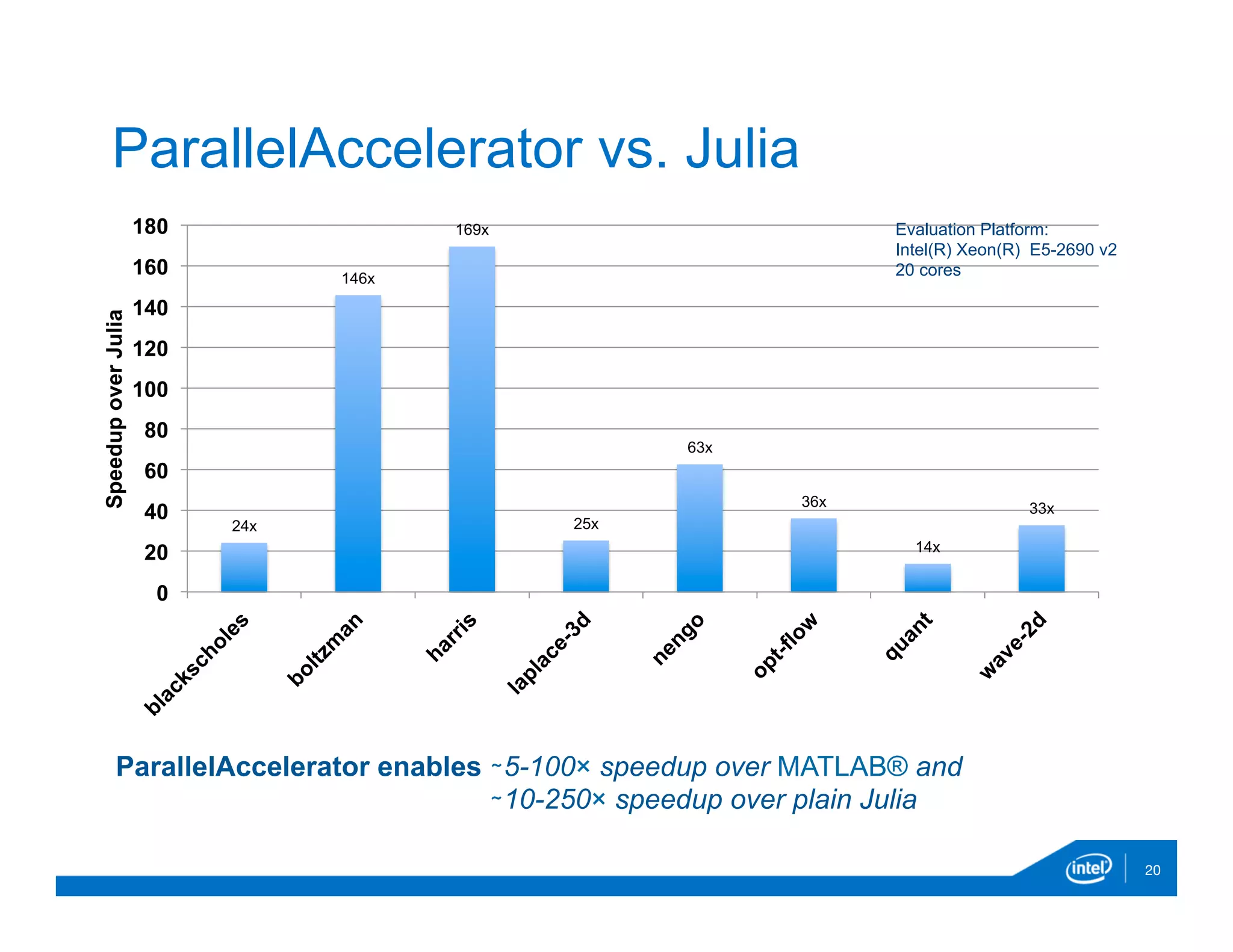
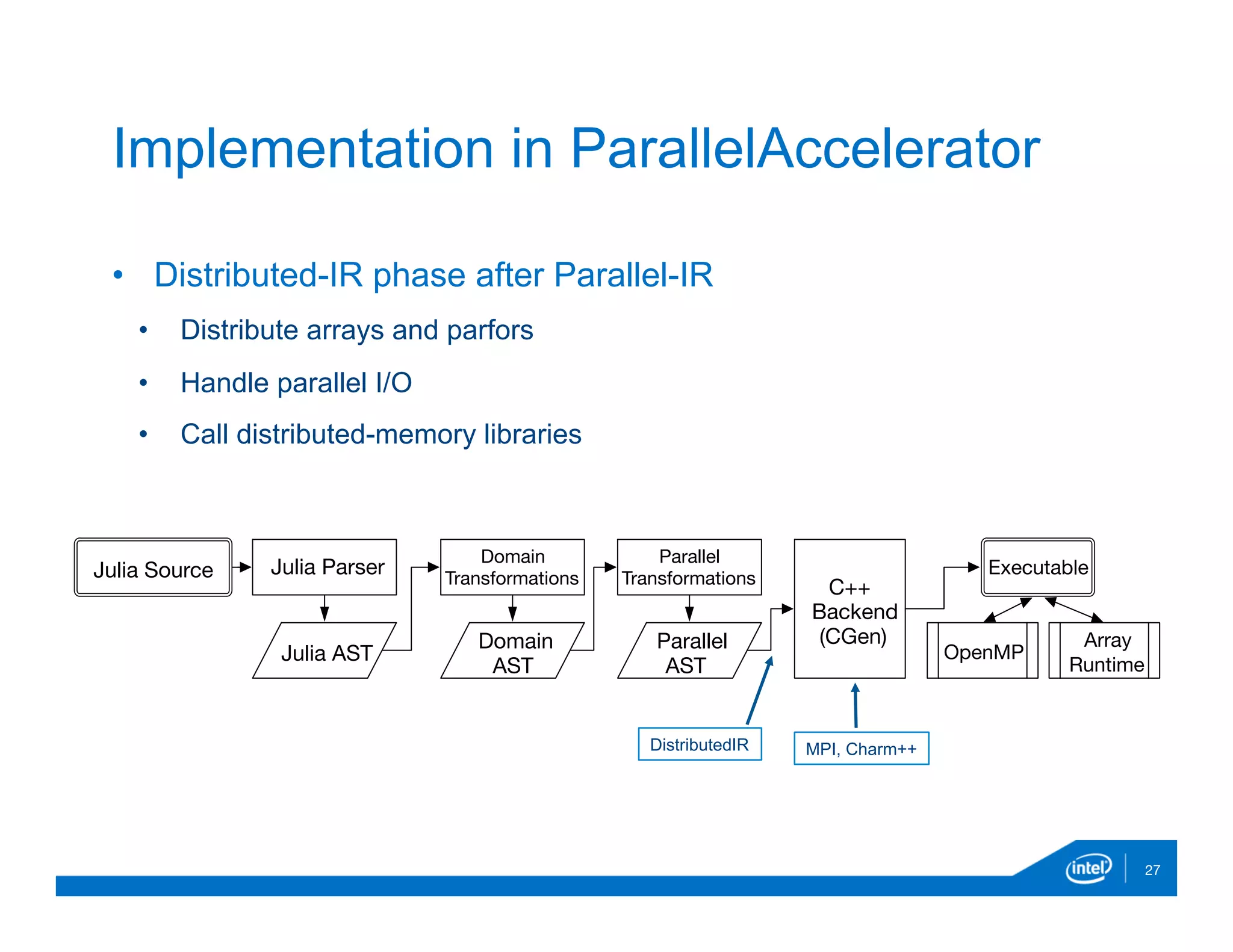
The document discusses the development and capabilities of 'parallelaccelerator.jl', a high-performance scripting tool designed for efficient parallel computing in Julia. It highlights the project's motivation, parallel programming patterns, notable performance improvements compared to MATLAB and Julia, along with installation, usage, and limitations. The future direction of the project includes enhancing native threading support and applying the tool in real-world data-intensive applications.

1. ParallelAccelerator.jl
High Performance Scripting in Julia
Ehsan Totoni
ehsan.totoni@intel.com
Programming Systems Lab, Intel Labs
December 17, 2015
Contributors: Todd Anderson, Raj Barik, Chunling Hu, Lindsey Kuper, Victor Lee, Hai Liu,
Geoff Lowney, Paul Petersen, Hongbo Rong, Tatiana Shpeisman, Youfeng Wu
1

2. § Motivation
§ High Performance Scripting(HPS) Project at Intel Labs
§ ParallelAccelerator.jl
§ How It Works
§ Evaluation Results
§ Current Limitations
§ Get Involved
§ Future Steps
§ Deep Learning
§ Distributed-Memory HPC Cluster/Cloud
2
Outline

3. HPC is Everywhere
3
Molecular
Biology
Aerospace
Cosmology
PhysicsChemistry
Weather
modeling
TRADITIONAL
HPC
Medical
Visualization
Financial
Analytics
Visual
Effects
Image
analysis
Perception
&Tracking
Oil
&
Gas
Exploration
Scientific
&
Technical
Computing
+Many-­‐core
workstations,
small
clusters,
and
clouds
Design
&
Engineering
Predictive
Analytics
Drug
Discovery
Large parallel clusters

4. HPC Programming is an Expert Skill
§ Most college graduates know
Python or MATLAB®
§ HPC programming requires C
or FORTRAN with OpenMP,
MPI
§ “Prototype in MATLAB®, re-
write in C” workflow limits
HPC growth
Source: Survey by ACM, July 7, 2014
Most popular introductory teaching
languages at top-ranked U.S. universities
“As the performance of HPC machines approaches infinity, the number of people who
program them is approaching zero” - Dan Reed
from The National Strategic Computing Initiative presentation
4

5. 5
High Performance Scripting
High Functional Tool Users
(e.g., Julia, MATLAB®, Python, R)
Ninja
Programmers
Increasing Performance
Increasing Technical Skills
Target
Programmer
Base for HPS
Average HPC
Programmers
Productivity
+
Performance
+
Scalability

6. Why Julia?
§ Modern LLVM-based code
§ Easy compiler construction
§ Extendable (DSLs etc.)
§ Designed for performance
§ MIT license
§ Vibrant and growing user
community
§ Easy to port from MATLAB® or
Python
Source: http://pkg.julialang.org/pulse.html
6

7. • Implemented as a package:
• @acc macro to optimize Julia functions
• Domain-specific Julia-to-C++ compiler written in
Julia
• Parallel for loops translated to C++ with OpenMP
• SIMD vectorization flags
• Please try it out and report bugs!
7
ParallelAccelerator.jl
https://github.com/IntelLabs/ParallelAccelerator.jl

8. A compiler framework on top of the Julia compiler for high-
performance technical computing
Approach:
§ Identify implicit parallel patterns such as map, reduce,
comprehension, and stencil
§ Translate to data-parallel operations
§ Minimize runtime overheads
§ Eliminate array bounds checks
§ Aggressively fuse data-parallel operations
8
ParallelAccelerator.jl

9. 9
ParallelAccelerator.jl Installation
• Julia 0.4
• Linux, Mac OS X
• Compilers: icc, gcc, clang
• Install, switch to master branch for up-to-date bug fixes
• See examples/ folder
Pkg.add("ParallelAccelerator")
Pkg.checkout("ParallelAccelerator")
Pkg.checkout("CompilerTools")
Pkg.build("ParallelAccelerator")

10. 10
ParallelAccelerator.jl Usage
• Use high-level array operations (MATLAB®-style)
• Unary functions: -, +, acos, cbrt, cos, cosh, exp10, exp2, exp, lgamma, log10, log, sin, sinh,
sqrt, tan, tanh, abs, copy, erf …
• Binary functions: -, +, .+, .-, .*, ./, .,.>, .<,.==, .<<, .>>, .^, div, mod, &, |, min, max …
• Reductions, comprehensions, stencils
• minimum, maximum, sum, prod, any, all
• A = [ f(i) for i in 1:n]
• runStencil(dst, src, N, :oob_skip) do b, a
b[0,0] = (a[0,-1] + a[0,1] + a[-1,0] + a[1,0]) / 4
return a, b
end
• Avoid sequential for-loops
• Hard to analyze by ParallelAccelerator

11. using ParallelAccelerator
@acc function blackscholes(sptprice::Array{Float64,1},
strike::Array{Float64,1},
rate::Array{Float64,1},
volatility::Array{Float64,1},
time::Array{Float64,1})
logterm = log10(sptprice ./ strike)
powterm = .5 .* volatility .* volatility
den = volatility .* sqrt(time)
d1 = (((rate .+ powterm) .* time) .+ logterm) ./ den
d2 = d1 .- den
NofXd1 = cndf2(d1)
...
put = call .- futureValue .+ sptprice
end
put = blackscholes(sptprice, initStrike, rate, volatility, time)
11
Example (1): Black-Scholes
Accelerate this
function
Implicit parallelism
exploited

12. using ParallelAccelerator
@acc function blur(img::Array{Float32,2}, iterations::Int)
buf = Array(Float32, size(img)...)
runStencil(buf, img, iterations, :oob_skip) do b, a
b[0,0] =
(a[-2,-2] * 0.003 + a[-1,-2] * 0.0133 + a[0,-2] * ...
a[-2,-1] * 0.0133 + a[-1,-1] * 0.0596 + a[0,-1] * ...
a[-2, 0] * 0.0219 + a[-1, 0] * 0.0983 + a[0, 0] * ...
a[-2, 1] * 0.0133 + a[-1, 1] * 0.0596 + a[0, 1] * ...
a[-2, 2] * 0.003 + a[-1, 2] * 0.0133 + a[0, 2] * ...
return a, b
end
return img
end
img = blur(img, iterations)
12
Example (2): Gaussian blur
runStencil
construct

13. 13
A quick preview of results
Data from 10/21/2015
Evaluation Platform:
Intel(R) Xeon(R) E5-2690 v2
20 cores
ParallelAccelerator is ~32x faster than MATLAB®
ParallelAccelerator is ~90x faster than Julia

14. • mmap & mmap! : element-wise map function
14
Parallel Patterns: mmap
(B1, B2, …) = mmap( (x1, x2, …) à (e1, e2, …), A1, A2, …)
n mm n
Examples:
log(A) ⇒ mmap (x → log(x), A)
A.*B ⇒ mmap ((x, y) → x*y, A, B)
A .+ c ⇒ mmap (x→x+c,A)
A -= B ⇒ mmap! ((x,y) → x-y, A, B)

15. • reduce: reduction function
15
Parallel Patterns: reduce
r = reduce(Θ, Φ, A)
Θ is the binary reduction operator
Φ is the initial neutral value for reduction
Examples:
sum(A) ⇒ reduce (+, 0, A)
product(A) ⇒ reduce (*, 1, A)
any(A) ⇒ reduce (||, false, A)
all(A) ⇒ reduce (&&, true, A)

16. • Comprehension: creates a rank-n array that is the cartesian
product of the range of variables
16
Parallel Patterns: comprehension
A = [ f(x1, x2, …, xn) for x1 in r1, x2 in r2, …, xn in rn]
where, function f is applied over cartesian product
of points (x1, x2, …, xn) in the ranges (r1, r2, …, rn)
Example:
avg(x) = [ 0.25*x[i-1]+0.5*x[i]+0.25*x[i+1] for i in 2:length(x)-1 ]

17. • runStencil: user-facing language construct to perform stencil
operation
17
Parallel Patterns: stencil
runStencil((A, B, …) à f(A, B, …), A, B, …, n, s)
m mm
all arrays in function f are relatively indexed,
n is the trip count for iterative stencil
s specifies how stencil borders are handled
Example:
runStencil(b, a, N, :oob_skip) do b, a
b[0,0] =
(a[-1,-1] + a[-1,0] + a[1, 0] + a[1, 1]) / 4)
return a, b
end

18. • DomainIR: replaces some of Julia AST with new “domain nodes” for
map, reduce, and stencil
• ParallelIR: replaces some of Domain AST with new “parfor” nodes
representing parallel-for loops (parfor)
• CGen: converts parfor nodes into OpenMP loops
18
ParallelAccelerator Compiler Pipeline
Domain
Transformations
C++
Backend
(CGen) Array
Runtime
Executable
OpenMP
Domain
AST
Parallel
AST
Julia Parser
Julia AST
Julia Source
Parallel
Transformations

19. • Map fusion
• Reordering of statements to enable fusion
• Remove intermediate arrays
• mmap to mmap! Conversion
• Hoisting of allocations out of loops
• Other classical optimizations
• Dead code and variable elimination
• Loop invariant hoisting
• Convert parfor nodes to OpenMP with SIMD code generation
19
Transformation Engine

20. 20
ParallelAccelerator vs. Julia
24x
146x
169x
25x
63x
36x
14x
33x
0
20
40
60
80
100
120
140
160
180
SpeedupoverJulia
ParallelAccelerator enables ∼5-100× speedup over MATLAB® and
∼10-250× speedup over plain Julia
Evaluation Platform:
Intel(R) Xeon(R) E5-2690 v2
20 cores

21. • Julia-to-C++ translation (needed for OpenMP)
• Not easy in general, many libraries fail
• E.g. if is(a,Float64)…
• Strings, I/O, ccalls, etc. may fail
• Upcoming native Julia path with threading helps
• Need full type information
• Make sure there is no “Any” in AST of function
• See @code_warntype
21
Current Limitations

22. • Not everything parallelizable
• Limited operators supported
• Expanding over time
• ParallelAccelerator’s compilation time
• Type-inference for our package by Julia compiler
• First use of package only
• Use same Julia REPL
• A solution: see ParallelAccelerator.embed()
• Julia source needed
• Compiler bugs…
• Need more documentation
22
Current Limitations

23. • Try ParallelAccelerator and let us know
• Mailing list
• https://groups.google.com/forum/#!forum/julia-hps
• Chat room
• https://gitter.im/IntelLabs/ParallelAccelerator.jl
• GitHub issues
• We are looking for collaborators
• Application-driven computer science research
• Compiler contributions
• Interesting challenges
• We need your help!
23
Get Involved

24. • ParallelAccelerator lets you write code in a
scripting language without sacrificing efficiency
• Identifies parallel patterns in the code and
compiles to run efficiently on parallel hardware
• Eliminates many of the usual overheads of high-
level array languages
24
Summary

25. • Make it real
• Extend coverage
• Improve performance
• Enable native Julia threading
• Apply to real world applications
• Domain-specific features
• E.g. DSL for Deep Learning
• Distributed-Memory HPC Cluster/Cloud
25
Next Steps

26. • Emerging applications are data/compute intensive
• Machine Learning on large datasets
• Enormous data and computation
• Productivity is 1st priority
• Not many know MPI/C
• Goal: facilitate efficient distributed-memory execution without
sacrificing productivity
• Same high-level code
• Support parallel data source access
• Parallel file I/O
26
Using Clusters is Necessary
http://www.udel.edu/
ParallelAccelerator.jl

27. • Distributed-IR phase after Parallel-IR
• Distribute arrays and parfors
• Handle parallel I/O
• Call distributed-memory libraries
27
Implementation in ParallelAccelerator
Domain
Transformations
C++
Backend
(CGen) Array
Runtime
Executable
OpenMP
Domain
AST
Parallel
AST
Julia Parser
Julia AST
Julia Source
Parallel
Transformations
DistributedIR MPI, Charm++

28. @acc function blackscholes(iterations::Int64)
sptprice = [ 42.0 for i=1:iterations]
strike = [ 40.0+(i/iterations) for i=1:iterations]
logterm = log10(sptprice ./ strike)
powterm = .5 .* volatility .* volatility
den = volatility .* sqrt(time)
d1 = (((rate .+ powterm) .* time) .+ logterm) ./ den
d2 = d1 .- den
NofXd1 = cndf2(d1)
...
put = call .- futureValue .+ sptprice
return sum(put)
end
checksum = blackscholes(iterations)
28
Example: Black-Scholes
Parallel
initialization

29. double blackscholes(int64_t iterations)
{
int mpi_rank , mpi_nprocs;
MPI_Comm_size(MPI_COMM_WORLD,&mpi_nprocs);
MPI_Comm_rank(MPI_COMM_WORLD,&mpi_rank);
int mystart = mpi_rank∗(iterations/mpi_nprocs);
int myend = mpi_rank==mpi_nprocs ? iterations:
(mpi_rank+1)∗(iterations/mpi_nprocs);
double *sptprice = (double*)malloc(
(myend-mystart)*sizeof(double));
…
for(i=mystart ; i<myend ; i++) {
sptprice[i-mystart] = 42.0 ;
strike[i-mystart] = 40.0+(i/iterations);
. . .
loc_put_sum += Put;
}
double all_put_sum ;
MPI_Reduce(&loc_put_sum , &all_put_sum , 1 , MPI_DOUBLE,
MPI_SUM, 0 , MPI_COMM_WORLD);
return all_put_sum;
} 29
Example: Black-Scholes

30. • Black-Scholes works
• Generated code equivalent to
hand-written MPI
• 4 nodes, dual-socket Haswell
• 36 cores/node
• MPI-OpenMP
• 2.03x faster on 4 nodes
vs. 1 node
• 33.09x compared to
sequential
• MPI-only
• 1 rank/core, no OpenMP
• 91.6x speedup on 144 cores
vs. fast sequential
30
Initial Results

31. Questions
31