The lecture covers optimization techniques for training neural networks, addressing challenges such as local minima, saddle points, and exploding gradients. It discusses various algorithms including stochastic gradient descent, momentum, and adaptive learning rates like Adam, which are essential for improving model performance. The importance of surrogate loss functions and early stopping in preventing overfitting and ensuring effective training is also highlighted.
![[course
site]
Verónica Vilaplana
veronica.vilaplana@upc.edu
Associate Professor
Universitat Politecnica de Catalunya
Technical University of Catalonia
Optimization for neural
network training
Day 4 Lecture 1
#DLUPC](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/75/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-1-2048.jpg)




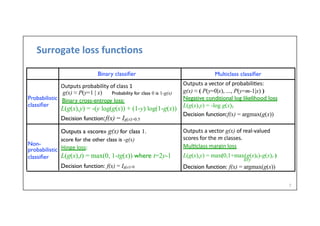
![Surrogate
loss
• O]en
minimizing
the
real
loss
is
intractable
• e.g.
0-‐1
loss
(0
if
correctly
classified,
1
if
it
is
not)
(intractable
even
for
linear
classifiers
(Marcoae
1992)
• Minimize
a
surrogate
loss
instead
• e.g.
nega.ve
log-‐likelihood
for
the
0-‐1
loss
• Some.mes
the
surrogate
loss
may
learn
more
• test
error
0-‐1
loss
keeps
decreasing
even
a]er
training
0-‐1
loss
is
zero
• further
pushing
classes
apart
from
each
other
6
0-‐1
loss
(blue)
and
surrogate
losses
(square,
hinge,
logis.c)
0-‐1
loss
(blue)
and
nega.ve
log
likelihood
(red)](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-6-320.jpg)
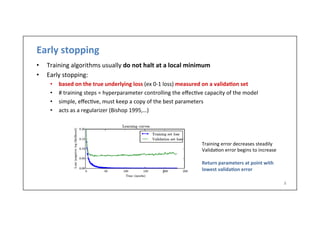








![Momentum
19
• Designed
to
accelerate
learning,
especially
for
high
curvature,
small
but
consistent
gradients
or
noisy
gradients
• Momentum
aims
to
solve:
poor
condi.oning
of
Hessian
matrix
and
variance
in
the
stochas.c
gradient
Contour
lines=
a
quadra.c
loss
with
poor
condi.oning
of
Hessian
Path
(red)
followed
by
SGD
(le])
and
momentum
(right)](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-19-320.jpg)

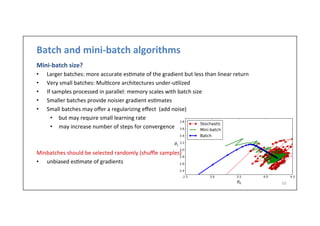
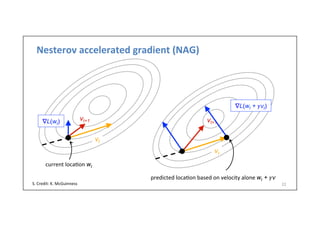
![Nesterov
accelerated
gradient
(NAG)
• A
variant
of
momentum,
where
gradient
is
evaluated
a]er
current
velocity
is
applied:
• Approximate
where
the
parameters
will
be
on
the
next
.me
step
using
current
velocity
• Update
velocity
using
gradient
where
we
predict
parameters
will
be
Algorithm
• Require:
learning
rate
α,
ini.al
parameter
θ,
momentum
parameter
λ
,
ini.al
velocity
v
• Update:
• apply
interim
update
• compute
gradient
(at
interim
point)
• compute
velocity
update
• apply
update
• Interpreta.on:
add
a
correc.on
factor
to
momentum
21
g ← +
1
m
∇!θ
L( f (x(i)
; !θ), y(i)
)i∑
θ ←θ + v
v ← λv −αg
!θ ←θ + λv](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-21-320.jpg)
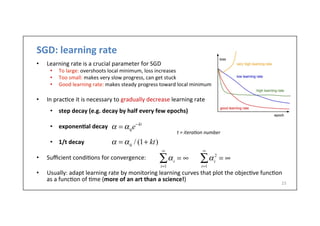
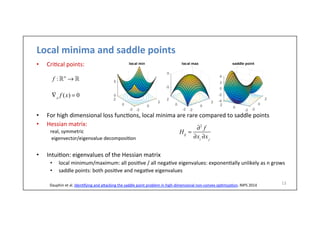
![Adap6ve
learning
rates
• Learning
rate
is
one
of
the
hyperparameters
that
is
the
most
difficult
to
set;
it
has
a
significant
impact
on
the
model
performance
• Cost
if
o]en
sensi.ve
to
some
direc.ons
and
insensi.ve
to
others
• Momentum/Nesterov
mi.gate
this
issue
but
introduce
another
hyperparameter
• Solu6on:
Use
a
separate
learning
rate
for
each
parameter
and
automa6cally
adapt
it
through
the
course
of
learning
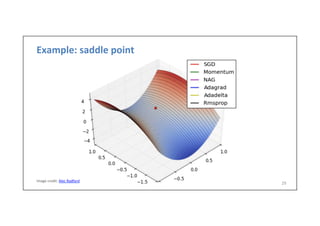
• Algorithms
(mini-‐batch
based)
• AdaGrad
• RMSProp
• Adam
• RMSProp
with
Nesterov
momentum
24](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-24-320.jpg)




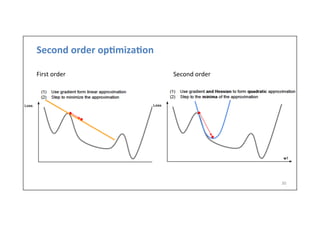


![Batch
normaliza6on
• As
learning
progresses,
the
distribu.on
of
the
layer
inputs
changes
due
to
parameter
updates
(
internal
covariate
shi])
• This
can
result
in
most
inputs
being
in
the
non-‐linear
regime
of
the
ac.va.on
func.on,
slowing
down
learning
• Bach
normaliza.on
is
a
technique
to
reduce
this
effect
• Explicitly
force
the
layer
ac.va.ons
to
have
zero
mean
and
unit
variance
w.r.t
running
batch
es.mates
• Adds
a
learnable
scale
and
bias
term
to
allow
the
network
to
s.ll
use
the
nonlinearity
33
Ioffe
and
Szegedy,
2015.
“Batch
normaliza.on:
accelera.ng
deep
network
training
by
reducing
internal
covariate
shi]”
FC
/
Conv
Batch
norm
ReLu
FC
/
Conv
Batch
norm
ReLu](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-33-320.jpg)
![Batch
normaliza6on
• Can
be
applied
to
any
input
or
hidden
layer
• For
a
mini-‐batch
of
N
ac.va.ons
of
the
layer
1. compute
empirical
mean
and
variance
for
each
dimension
D
2. normalize
• Note:
normaliza.on
can
reduce
the
expressive
power
of
the
network
(e.g.
normalize
intputs
of
a
sigmoid
would
constrain
them
to
the
linear
regime
• So
let
the
network
learn
the
iden.ty:
scale
and
shi]
• To
recover
the
iden.ty
mapping
the
newtork
can
lean
34
ˆx(k )
=
x(k )
− E(x(k )
)
var(x(k )
)
N
D
X
β(k )
= E(x(k )
)γ (k )
= var(x(k )
)
y(k )
= γ (k )
ˆx(k )
+ β(k )](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-34-320.jpg)


![Summary
37
• Op.miza.on
for
NN
is
different
from
pure
op.miza.on:
• GD
with
mini-‐batches
• early
stopping
• non-‐convex
surface,
local
minima
and
saddle
points
• Learning
rate
has
a
significant
impact
on
model
performance
• Several
extensions
to
SGD
can
improve
convergence
• Ada.ve
learning-‐rate
methods
are
likely
to
achieve
best
results
• RMSProp,
Adam
• Weight
ini.aliza.on:
He
w=
randn(n)
sqrt(2/n)
• Batch
normaliza.on
to
reduce
the
internal
covariance
shi]](https://image.slidesharecdn.com/dlai2017d4l1optimization-171101161756/85/Optimization-DLAI-D4L1-2017-UPC-Deep-Learning-for-Artificial-Intelligence-37-320.jpg)
