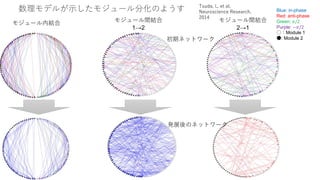
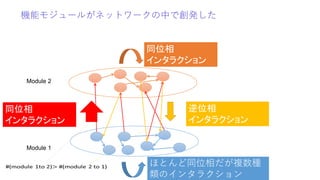
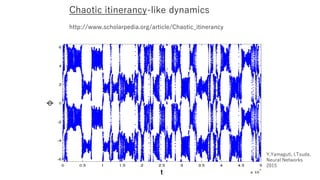
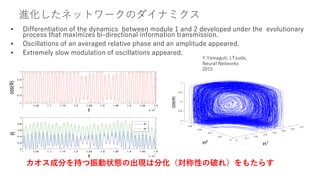
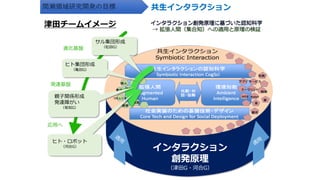
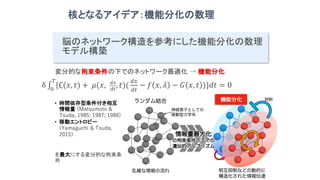
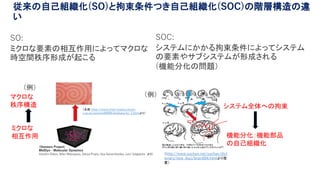
講演者：津田 一郎（中部大学創発学術院） 概要：学習するニューラルネットとプログラム駆動型の人工知能の融合は1980年代から始まり今日の爆発的な進展へと至っています。この融合研究の進展の中で、私たちは創発インタラクションの果たす役割は大きいと考えています。私たちは CREST の共生インタラクション領域 (https://www.jst.go.jp/kisoken/crest/research_area/ongoing/bunyah29-4.html) の中のプロジェクト (http://www.er.ams.eng.osaka-u.ac.jp/kawai/crest/) において特に脳の進化的及び機能的結合を介した機能分化に着目し、複雑な環境に対して機能分化を通じて即時適応する機構の解明とそれを実現するエージェントの提案を目指して研究を開始しました。講演では脳の機能分化を変分原理で定式化する試みと具体的な数理モデルの結果をお話しする予定です。

1. 創発インタラクションの意義：
機能分化に対する変分原理と数理モデル
津田一郎
中部大学創発学術院
全脳アーキテクチャー勉強会
＠東大医学部鉄門講堂、２０１８年６月２８日

2. 自己紹介にかえて：科学史のなかでの個人的問題意識

3. 乱流：Kolmogorov
Y.G.Sinai
富田和久 先生（右）
山口昌哉 先生（左）
非線形力学系・カオス力学系（双曲型力学系）の理論
↓
非双曲型カオス力学系
カオス遍歴の概念と５つのシナリオ
脳のダイナミクスの機能的解釈（脳の解釈学）
脳と心をつなぐ数学
情報理論、計算理論： C. Shannon, A. Turing
カオスの情報理論
複雑系数理学
熱力学（平衡系）→ 非線形熱力学（非平衡系）
↑ ↑ ⇒ 非線形・非平衡系の現象論
統計力学（平衡系） 散逸構造(I.Prigogine)
→ 線形応答理論・搖動散逸定理（近平衡系） 隷属原理（H. Haken）
形態形成： R. Thom カタストロフ理論 → 一般カタストロフ
⇒
カオス現象（エルゴード理論の一般化現象）、
分岐現象（相転移現象の一般化）← 分岐理論

4. [
「心はすべて数学である」
・名古屋学院大学
H29年度前期入試
国語問題Iに採用
・安田女子大学
H30年度前期入試
国語問題に採用
・理研x編集工学研究所選
「科学道１００冊」に選出
2015
2016
2002 2002
1990 2001
1996 2006
2006 2006 2011 2006

5. 脳科学への寄与
１．脳の解釈学
２．記憶のダイナミックな遷移の一機構
３．思考・推論のダイナミクスと数学的構造
４．エピソード記憶形成の数学的構造
５．コミュニケーション神経情報学の創始
６．脳の病態の数理モデルと病態データに潜む数学構造
（拘束条件付きに自己組織化された構造）の抽出
数学への寄与
１．非双曲型力学系のいくつかの数学的構造の解明：
・カオス遍歴
・特異連続でいたるところ微分不可能なアトラクター
・Noise-induced order
・Milnor attractorの応用
２．複雑系科学に対する数理科学的枠組みの構築：
斜積変換、結合力学系、構造安定性の拡張： 記述安定性
３．拘束条件付き自己組織化理論の提案
４．数学の拡がり運動
（JST クレスト、さきがけ数学領域；
文科省研究振興局基礎研究振興課数学イノベーションユニットなど）
今日の本題

6. I. Gelfand のmathematics as an adequate language
に触発されて、
脳のmathematics as an adequate languageを探す
S. Smaleの第１８問題：
自然知能と人工知能の限界を定めよ。
I. Gelfand: C*環、超関数、表現論；１９８９年京都賞、１９７９年ウルフ賞数学部門
S. Smale: 可微分多様体、微分可能力学系（馬蹄形写像：カオス）、
実数計算論；１９６６年フィールズ賞

7. Resonance between two brains
(Visual Cues) Schippers et.al, PNAS, 2010

8. Speaker–listener neural coupling
underlies successful communication
(Auditory Cues) Greg J. Stephens et al., PNAS, 2010

9. A B
Learning of others’ memories
A B
A B
Recall of own memories
コミュニケーションにおける脳ダイナミクスの数理科学的研究
(新学術領域Ｈ２１－２５：伝達創成機構）
カオス的遍歴の
さまざまな機能
コミュニケーションに伴う神経
機構の数学による解明
⇒ コミュニケーション神経情
報学
9
・ダイナミックな記憶過程
・ミラーニューロン問題
・ダイナミックな推論過程
と想像能力
・共感：類似の力学系と同期

10. Internal state of the brain
via mind
Body/Intention/participation
Body/Sensation/Environmental ChangeEnvironment
人の知覚は離散的；予測をするから連続的に見える
𝑍 𝑛+1 = 𝐹(𝑍 𝑛)
ൗ𝑑𝑥
𝑑𝑡 = 𝑃(𝑥)
Hermeneutic circle (解釈学的循環）

11. 作業仮説：「心はすべて数学である」（文芸春秋、津田、２０１５年）より
cf 「脳のなかに数学を見る」（共立出版、津田、２０１６年）
普遍的な心が生物学的器官である脳を形成する。
普遍的な心が個々の脳を通過するとき個々の心が生まれる。
数学は普遍的な心を求めてきたのではないか。
数学は心を表現している

12. 数学は普遍心を表現する
普遍心は生物学的器官としての脳を形成する。
個々の心は普遍心が個々の脳を通過するときに生まれる。
数学の基礎は心の基本作用の集合からなる ：
数を数える、面積を測る、物事の同一性を認知する、時間・空間を知覚する、等
Universal mind math コミュニケーションを介した
環境変数(普遍心）からの影響
孤立脳モデルとしての力学系
力学系の変化を介した発展系
心のコアー: 記憶、思考・推論、感覚・知覚、感性、想像、意志

13. カオスとは何か？
カオスは時間方向に情報を開く
時間の矢の両方向に拡大作用かつ縮小作用を持つ
局所的な縮小と拡大
相空間
時間

14. ロバチェフスキー空間(双曲空間）での表現 (by Y.G.Sinai)

{ }C
{ }C
t  t  
時間の正の方向にも負の方向にも互いに漸近する軌道の束が存在する

15. ポアンカレ計量：単位円盤𝐷 = 𝑧 = 𝑥 + 𝑖𝑦: 𝑧 = 𝑥2 + 𝑦2 < 1 上
𝑑𝑠2 =
𝑑𝑧𝑑𝑧
(1− 𝑧 2)2
距離： 𝜌 𝑧1, 𝑧2 = tanh−1 𝑧1−𝑧2
1−𝑧1 𝑧2
tanh−1
𝑥 =
1
2
𝑙𝑜𝑔
1 + 𝑥
1 − 𝑥

16. 複雑系とは？
Complex systems: 系をより単純な要素に分解して理解することができない。要素は
系全体の状態によって逆に規定される。例）脳の機能分化、胚発生に典型的に見られる。
因果関係が多対多、あるいは非因果的。
cf) Complicated systems: 因果関係が一対一に決められるような単純な系の複合体。
⇒ カオス的な系では初期値と運動方程式が必ずしも独立ではない。
⇒ 生命的なシステムでは、外部から与えられた初期条件、境界条件が系の状態、
行動を必ずしも決定しない。内部で生み出された条件が系の状態,行動を決定する。
↳創発
物理学： 富田和久（非線形非平衡統計力学；カオス）
I. Prigogine （散逸構造論；非線形非平衡の熱力学、１９７７年ノーベル化学賞）
H. Haken （シナジェティクス）
数学：山口昌哉（非線形数学；カオス）+ 山口組
R. Thom（カタストロフィー理論；セミオフィジクス； 微分可能多様体 １９５８年フィールズ賞)
J. Yorke（カオス；２００３年日本国際賞（複雑系の科学技術分野））
B. Mandelbrot（フラクタル幾何学；２００３年日本国際賞（複雑系の科学技術分野））

17. 複雑系科学研究の歴史
第１期： 第一次大戦後
ゲシュタルト心理学、
創造的進化（H. Bergson）： 創成と発展の生物進化 全体性(totality)
第２期： 第二次大戦後
サイバネティクス（N. Wiener）： 複雑現象の数学研究：
確率微分方程式による複雑時系列の解析
⇒ フィードバック制御、予測理論、フィルター、ホワイトノイズ解析 普遍性(universality)
第３期： １９８０年代以降
非線形非平衡系：カオス力学系とフラクタル幾何学
複雑ネットワーク（P. Erdösのランダムネットワーク理論がおおもと）
繰り返しと決定論的複雑性(deterministic
complexity)
第４期：２０００年以降
インターネット、IoTの時代：環境自体が複雑なネットワーク
機能分化（functional differentiation）
今いるところ

18. 脳領域／個体／集団間の
インタラクション創発原理
の解明と適用
津田一郎
中部大学・創発学術院
間瀬領域キックオフミーティング
@市ヶ谷コンファレンスセンター
平成29年11月1日(水)
TOKUSUI Meeting on December 18, 2015
@Osaka Univ.（H29-H34年度）
研究領域「人間と情報環境の共生インタラクション基盤技術の創出と展開」
（研究総括：間瀬 健二、H２９年度発足）

19. 津田チームイメージ インタラクション創発原理に基づいた認知科学
→ 拡張人間（集合知）への適用と原理の検証
インタラクション
創発原理
（津田G・河合G）
進化基盤
応用へ
発達基盤
ヒト集団形成
（亀田G）
ヒト・ロボット
（河合G）
親子関係形成
発達障がい
（菊知G）
間瀬領域研究開発の目標 共生インタラクション
サル集団形成
（松田G）

20. 課題提案：本領域の観点において
1. システムに拘束条件がかかることで機能的なシステム 部品（成分）が自己組織される原理は何
か？
2. 人間社会において個より機能の優れた集合知が可能か？
これらを
• 数学・情報科学技術
• 認知科学
• 社会科学
• 脳科学等の学問分野
の学問分野と連携し，
• 人間理解
• 社会デザイン
• 構成論的アプローチ
の共創により解決

21. 研究チーム構成
1. 創発原理グループ
津田研究代表(中部大学）
2. 脳領域間・ロボットグループ
河合共同研究者(大阪大学）
3. 個体内／個体間グループ
菊知共同研究者(金沢大学）
5. 集団内／集団間グループ
亀田共同研究者(東京大学）
4. 個体間／集団間グループ
松田共同研究者(中部大学）

22. 核となるアイデア：機能分化の数理
脳のネットワーク構造を参考にした機能分化の数理
モデル構築
• 時間依存型条件付き相互
情報量 (Matsumoto &
Tsuda, 1985; 1987; 1988)
• 移動エントロピー
(Yamaguchi & Tsuda,
2015)
変分的な拘束条件の下でのネットワーク最適化 → 機能分化
を最大にする変分的な拘束条
件
δ ‫׬‬0
𝑇
{∁(𝑥, 𝑡) + 𝜇(𝑥, 𝑑𝑥
𝑑𝑡
, 𝑡)(
𝑑𝑥
𝑑𝑡
− 𝑓 𝑥, 𝜆 − 𝐺 𝑥, 𝑡 )}𝑑𝑡 = 0

23. 従来の自己組織化(SO)と拘束条件つき自己組織化(SOC)の階層構造の違
い
ミクロな
相互作用
マクロな
秩序構造
機能分化：機能部品
の自己組織化
システム全体への拘束（北畑：http://www.chem.scphys.kyoto-
u.ac.jp/nonnonWWW/kitahata/bz_1.htmlより）
（Honours Project:
MolDyn - Molecular Dynamics
Veselin Dikov, Niko Manopulo, Darya Popiv, Ilya Saverchenko, Levi Valgaerts より）
（例）
（http://www.yuchan.net/yuchan/dict
ionary/new_ikuji/brain004.htmlより改
変）
（例）
SO:
ミクロな要素の相互作用によってマクロな
時空間秩序形成が起こる
SOC:
システムにかかる拘束条件によってシステム
の要素やサブシステムが形成される
(機能分化の問題）

24.  カオス遍歴の極小モデル（I.Tsuda et al, 1987）の存在が31年後
に数学的に証明された（R.B. Liberalquino et al, 2018）
非平衡神経回路網が生みだす動的連想記憶を支配する円周写像
𝜃 𝑛+1 = 𝜃 𝑛 + 𝜔 − 𝐴𝑠𝑖𝑛 2𝜋𝜃 𝑛 (𝑚𝑜𝑑 1)
 ノイズによる混沌からの秩序（Noised-induced order,
K. Matsumoto and I. Tsuda, 1983）の存在が３５年後に数学的
に証明された（S. Galatolo, M. Monge, I. Nisoli, 2017）
ノイズなし
１％のノイズ
ノイズによるエントロピーの減少

25. 拘束条件付き自己組織化理論の適用例
１．力学系ネットワークの進化ダイナミクスから要素としての
ニューロンとニューラルネットが自発生成
(Watanabe, H., Ito, T., Tsuda, I., 2011; 2018)
２．振動型ニューロンネットワークの進化ダイナミクスから構造的に異なる
モジュールが分化(Yamaguti, Y., Tsuda, I., 2015; 2018)
３．非シナプス性結合における同期する進行波解の存在条件の導出
(Tsuda, I. Yamaguti, Y., H. Watanabe, 2016)
４．レビー小体型認知症患者が経験する複合型視覚性幻覚の神経機構解明
へ向けて (Tsukada, H, Fujii, H., Aihara, K., Tsuda, I., 2015；
Todo et al, 2018)
北大工学部郷原研
𝐿 𝑘
+
𝑔 𝑘 𝑧 = 0 with 𝑔 𝑘 𝑧 = 0 as 𝑧 → ∞,
‫׬‬−∞
∞
𝑔 𝑘 𝐹𝑘 𝑑𝑥 = 0.⇒ 変分逆問題へ
⇒ 医療応用へ
⇒ 一般的なネットワークでの可能性を追求
⇒ 複数入力系に拡張
2013年10月2日NHK
特集番組より,
drawn by a court
artist

26. 拘束条件のある力学
１．ホロノミック力学：
・無限小変化の自由度と大域的変化の自由度が一致している：積分可能
２．非ホロノミック力学：
・無限小変化の自由度と大域的変化の自由度が一致しない：積分不可能
・ダランベール原理（仮想仕事の原理：反作用は仕事をしない）
・ラグランジュ未定乗数を消去する：フィードバック制御
（汎関数の極値から拘束条件に従うものを選択）
・因果的
３．バコノミック力学（Vakonomic mechanics by V.V.Kozlov）：
・変分原理：ラグランジュ未定乗数は独立変数で初期状態、終状態に依存
⇒ Final state sensitivity
・最適制御理論（アンドロノフ・ポントリャーギン）
（変分多様体上で拘束条件をかけて極値を求める）
・非因果的

27. (1)数学でニューロンを作る：ニューロンはいかにして生まれたか？
Watanabe, H., Ito, T., Tsuda, I.: Making a neuron model: A mathematical approach.
In: 11th meeting of Mechanisms of Brain and Mind, Niseko, Hokkaido , Japan, Jan. 11−13, (2011)
Watanabe, H., Ito, T., Tsuda, I., to be submitted, 2018.

28. 後期初期
進化のステージ
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
xn i
site k
site k
変化・発展する力学系
Mutual information I
( 1)x t 
( )x t
iteration t
iteration t
( 1) ( )x t x t  状態変化の規則：
写像で表現
入力時系列が有する情報量
の時間空間変化
入力時系列の時間空間変化

29. 後期初期
進化のステージ
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
1.5
2
0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
xn i
site k
site k
Mutual information I
( )x t
( 1)x t 
iteration t
iteration t
( 1) ( )x t x t 

30. 0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
1.5
後期初期
進化のステージ
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
1.5
2
0
1
2
3
4
5
6
7
8
9
0 20 40 60 80 100
0.5
1
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
6
7
8
9 0 5 10 15 20 25 30
0
0.5
1
1.5
2
2.5
3
3.5
xn i
site k
site k
Mutual information I
( 1)x t 
( )x t
iteration t
iteration t
( 1) ( )x t x t 

31. x1, x2: 初期状態
閾値
閾値
静止状態
x1 x2
X(t)
X(t+1)
X(t+1)=X(t)
ニューロンと類似の興奮性を持つ要素が
ネットワークの中に創発した
電位
時間

32. (2) 機能モジュールの生成
Tsuda, I., Yamaguti, Y., Watanabe, H.:
Modeling the Genesis of Components in the Networks of Interacting
Units. Proc. of ICCN 2013.
Yamaguti, Y., Tsuda, I.: Mathematical Modeling for Evolution of
Heterogeneous Modules in the Brain.
Neural Networks 62: 3-10 (2015)
Yutaka Yamaguti, Ichiro Tsuda, Yoichiro Takahashi
Information flow in heterogeneously interacting systems, Cog.
Neurodynamics 8:17-26, 8 (2014)

33. 脳のモジュール間の結合は非対称結合
Felleman & Van Essen 1991
I-III
IV
V-VI
I-III
IV
V-VI
Ascending (Feed Forward) Projections
I-III
IV
V-VI
I-III
IV
V-VI
Descending (Feed Back) Projections
“Higher” region “Lower” region
視覚野のモジュール間結合
Y.Yamaguti, I.Tsuda, Y. Takahashi,
2014

34. ブロードマンの機能地図:
構造的な分化が機能的な分化をもたらす
大脳新皮質のモジュール化
構造的な分化
機能分化

35. 海馬におけるCA3-CA1の分化：爬虫類（小細胞層と大細胞層の一様ランダムネッ
ト ）から
哺乳類（リカレントネット＋フォワード型ネット）へ
Treves, A. (2004). Hippocampus, 14(5), 539–56.

36. Network model
• The dynamics of each oscillator is defined by
𝜃𝑡+1
(𝑖,𝑘)
= 𝜔
(𝑖,𝑘)
+ 𝜃𝑡
(𝑖,𝑘)
+
𝛼
𝑁𝑝 𝑐
෍
(𝑗,𝑙)∈𝐺
(𝑖,𝑘)
sin 𝜃𝑡
(𝑗,𝑙)
− 𝜃𝑡
𝑖,𝑘
− 𝜓 𝑘𝑙
𝑖𝑗
+ 𝜎𝛽 𝛽𝑡
(𝑖,𝑘)
for k th oscillator in i th module.
• 𝛼 is a coupling strength and 𝛽𝑡
(𝑖,𝑘)
represents an additive Gaussian noise which
applied to each oscillator, independently. Each 𝜓 𝑘𝑙
𝑖𝑗
is assigned one of four
possible values 0,
𝜋
2
, 𝜋,
3𝜋
2
randomly, according to probabilities 𝑝 𝑚
𝑖𝑗
(m=0,…3).
・We use the probability vectors 𝑝 𝑖𝑗 = 𝑝0
𝑖𝑗
, … , 𝑝3
𝑖𝑗
to regulate the mixing ratio of four kinds of connections from
module j to i. 𝑝0
𝑖𝑗
> 0, σ 𝑚 𝑝 𝑚
𝑖𝑗
= 1.

37. 数理モデルが示したモジュール分化のようす
モジュール内結合 モジュール間結合
1→2
モジュール間結合
2→1
Blue: in-phase
Red: anti-phase
Green: 𝜋/2
Purple: −𝜋/2
○：Module 1
●: Module 2
発展後のネットワーク
初期ネットワーク
Tsuda, I., et al,
Neuroscience Research,
2014

38. 機能モジュールがネットワークの中で創発した
同位相
インタラクション
逆位相
インタラクション
ほとんど同位相だが複数種
類のインタラクション
同位相
インタラクション
Module 1
Module 2

39. Chaotic itinerancy-like dynamics
http://www.scholarpedia.org/article/Chaotic_itinerancy
Y.Yamaguti, I.Tsuda,
Neural Networks
2015

40. 進化したネットワークのダイナミクス
• Differentiation of the dynamics between module 1 and 2 developed under the evolutionary
process that maximizes bi-directional information transmission.
• Oscillations of an averaged relative phase and an amplitude appeared.
• Extremely slow modulation of oscillations appeared.
カオス成分を持つ振動状態の出現は分化（対称性の破れ）をもたらす
Y.Yamaguti, I.Tsuda,
Neural Networks
2015

41. A
B
C
D
E
L1
𝑅 𝑚
or 𝑀
L2 chaotic itinerancy
(Ikeda-Kaneko-Tsuda,
1989,90,91.....)
I. Tsuda, Current Opinion in Neurobiology 2015, 31:67–71
http://www.scholarpedia.org/article/Chaotic_itinerancy
Dynamics between
default modes can be
represented
by chaotic itinerancy

42. Ω
evoked
Instability
via
Interventions
(constraints)
Similar but slightly different invariant manifolds
脳は外部刺激があるときは低次元の
不変多様体上に制限された活動をする
→ intrinsic manifolds (Luczak et al. 2009)
カオス的解釈
D
E
L1
A
B
L2
Chaotic itinerancy
脳は外部刺激がないときは
不変多様体間を遍歴する
Excess pruning via anti-Hebbian
learning
意識Ｕ無意識

43. Cooperative and/or
competitive interactions
between elementary units
Emergence of
order
parameters
Macroscopic
constraints
Emergence of
elementary units, or
components
(a) 自己組織化（SO） (b) 拘束条件付き自己組織化（SOC）
cf) For sensorimotor control,
M. Haruno, DM. Wolpert, M. Kawato,
MOSAIC

44. ディスカッション：創発インタラクションの必須概念
１．教師あり学習から教師なし学習への転換：自律性 (C1)
cf) AlphaGo-zeroの自律性？強化学習の導入
２．特徴抽出のみでなく、環境に応じて新しい機能の追加：万能性 (C0 & C1)
３．共感などの他者性と自己意識の生成：インタラクション、自己言及 (C2)
４．動機付けの機構：アフォーダンスへのアテンションとアダプテーション(AAA)
(C2)
５．時間概念の獲得；未来を想像；未来からの視座：現存在 (C3)
６．歴史性と文化を内包：解釈機能 (C3)
７．Abduction(仮説生成）→Deduction（仮説から結論）→Induction（結論から
法則）の循環：仮説生成 (C3)

45. （付録）
海馬におけるエピソード記憶形成の理論と数理モデル

46. 脳における時間空間概念はいかに構築されるのか?
⇒ カントのアプリオリ時間・空間概念を神経活動によって証
明できるか？
海馬における場所細胞の発見 (O’Keefe and Nadel 1978)
内嗅野におけるグリッド細胞の発見(Fyhn, Molden, Witter, Moser,
Moser 2004)
O’Keef, E. Moser, M. Moser ２０１４年度ノーベル医学生理学賞
⇒ 人の空間認識に対する神経基盤の構築へと発展すべき
発見されたＧＰＳ機能がカントのアプリオリな空間概念を与えうるかどうかは今後
の課題

47. 人の時間認識能力の神経基盤は何か ?
⇒
カントのアプリオリな時間概念の神経科学的解明は可能か?
Circadian rhythms regulated by the suprachiasmatic nucleus,
which are entrained by the earth’s rotation period
Time cells が発見されている：
・temporal sequences (迷路におけるラットの経験）(Eichenbaum 2014)
・time lapse （刺激提示後の経過時間）(Howard et al. 2014).
time lapse に関する理論： Shanker and Howard (2012).

48. V(t, s) : ニューロンの膜電位,
s 減衰定数
F(t): 外部刺激
𝑑𝑉(𝑡, 𝑠)
𝑑𝑡
= −𝑠𝑉 𝑡, 𝑠 + 𝐹(𝑡)
𝑉 𝑡, 𝑠 = න
−∞
𝑡
𝐹 𝑡′ 𝑒 𝑠(𝑡′−𝑡) 𝑑𝑡′⇒
外部刺激のラプラス変換
Leaky integrator
time
𝐹(𝑡)
𝑉 𝑡, 𝑠

49. (1) Approximate formula of inverse Laplace transform (E. Post, 1930):
delay period (time cells coding)
T(t, t*) =
−1 𝑘
𝑘!
𝑠 𝑘+1 𝑉 𝑘 𝑡, 𝑠 , 𝑤ℎ𝑒𝑟𝑒 𝑠 = − Τ𝑘
𝑡∗ 𝑡 ∗ < 0
𝑇 = ෨𝐿−1
(𝑉) 𝑇 𝑡, 𝑡 ∗ ≅ 𝐹(𝑡 + 𝑡 ∗)
(2) Phase space transformation : spacialization of time information
temporal sequences of events
(Cantor coding: I.Tsuda 1995-2016; Fukushima et al, 2009-2016)
𝑓1(𝑥)= 𝑎1 𝑥 + 𝑏1, ⋯ , 𝑓𝑛 𝑥 = 𝑎 𝑛 𝑥 + 𝑏 𝑛
One of the affine transformations is selected in CA1,
depending on the output pattern of CA3.

50. Cantor coding with chaotic input time series
海馬における時間情報のコーディングの神経機構の解明
海馬CA3, chaotic itinerancy: エピソードの系列の表現
海馬CA1, Cantor sets: 状態空間での時間系列の空間化 (相空間変換).

51. エピソード記憶のカントールコーディング仮説
経験事象の系列の脳内記憶システムに関する予言
⇒ 実験的検証
(福島、塚田ら玉川大学の実験 Cogn. Neurodyn. (2007)1: 305-316. ）
非線形ダイナミクス理論 経験の文脈依存的階層処理
t1t 2t 
経
験 ・・・
1t  2t  3t  
近過去 遠過去
脳内記憶システム

52. Henry Gustav Molaison (H.M.)
Molaison’ surgery in 1953
Born February 26, 1926, Hartford, Conneticut
Died December 2, 2008, Windsor Locks, Conneticut
He had suffered from
heavy epileptic seizures,
then he was operated upon
removing the hippocampus.
He, then, suffered from heavy
anterograde amnesia, and
moderate retrograde amnesia,
although his procedural
memories and working memory
are intact.

53. A skeleton network
of the hippocampus
● Unidirectional connections: CA3→CA1
(Mishkin 1982)
Experimental
finding on
the dynamics in
the hippocampus
Buzsaki; Toth, et al
⋆ Chaotic activity was observed in rat CA3 pyramidal cells.
(Hayashi & Ishizuka)
⋆ LTP can be enhanced by the input time series of intermittency.
(Tatsuno & Tsukada)
● Recurrent connections in CA3
Many theories and mathematical models have been proposed: Rolls, Traub, Treves,
Tsukada, Hasselmo, McNaughton, Yamaguchi, Hayashi, Erdi, and many others.
Chaos-driven contracting
System:
A skew product
transformation

54. Skew-product Transformations
For ( , ) ,x y M N 
Example. →
: , ( ),
: ,( , ) ( )
: , ( , ) ( ( ), ( ))
x x
x
M M x x
M N N x y y
M N M N x y x y
 
 
   

 

  
If for
then
is called a direct product
transformation.
, xx M  
 
( , ) ( ( ), ( ))x y x y  
is a skew product transformation.

55. • Emergence of affine
transformations (IFS)
y→Ay+b
Return map of each principal component of the membrane
potentials of CA1
1st component
2nd component 3rd component
y’= μy
y’= μy + 1 - μ
Which branch is adopted
is determined, depending
on chaotic variable.
A skew product
transformation
y
y’

56. カントル集合 (G. Cantor)
１．閉集合
２．全不連結
３．完全
カントル集合はフラクタル集合である
カントル集合による時系列情報（エピソード記憶）の埋め込み

57. Experiments:
Collaborated with
M.Tsukada and
Y. Fukushima,
Tamagawa Univ.
Y. Fukushima, et al,
Cogn Neurodyn, 1(2007) 305–316.

58. CA1 dynamics：
Typical clustering of membrane potentials of CA1
neurons observed in laboratory
( S. Kuroda et al. Cogn. Neurodyn. 2009)

59. Emergence of affine transformations (Kuroda et al, Cogn. Neurodyn. 2009)

60. References on Chaotic Itinerancy and Cantor Coding
Recent works on Chaotic itinerancy
Tsuda I (2015) Chaotic itinerancy and its role in cognitive neurodynamics. Curr. Opin. Neurobio. 31: 67−71.
Tsuda I (2013) Chaotic itinerancy. Scholarpedia 8(1):4459. DOI: 10.4249/scholarpedia.4459
http://www.scholarpedia.org/article/Chaotic_itinerancy
Kaneko K, Tsuda I (2003) Chaotic Itinerancy.Chaos, 13: 926−936
Cantor coding
Yamaguti Y, Kuroda S, Fukushima Y, Tsukada M, Tsuda I ( 2011) A mathematical model for Cantor coding in the
hippocampus. Neur. Net. 24: 43−53
Kuroda S, Fukushima Y, Yamaguti Y, Tsukada M, Tsuda I (2009) Iterated function systems in hippocampal CA1. Cogn.
Neurodyn. 3: 205−222.
Fukushima Y, Tsukada M, Tsuda I, Yamaguti Y, Kuroda S (2007) Spatial clustering property and its self-similarity in
membrane potentials of hippocampal CA1 pyramidal neurons for a spatio-temporal input sequence. Cogn.
Neurodyn. 1: 305−316
Tsuda I, Kuroda S (2001) Cantor coding in the hippocampus. Japan. J. Indus. Appl. Math. 18: 249−258
Tsuda I, Yamaguchi A (1998) Singular-continuous nowhere-differentiable attractors in neural systems.
Neur. Net. 11: 927−937
Tsuda I (1996) A new type of self-organization associated with chaotic dynamics in neural systems.
Int. J. Neural Sys. 7: 451−459
Chaotic itinerancy & Cantor coding
Tsuda I (2009) Hypotheses on the functional roles of chaotic transitory dynamics. Chaos 19: 015113-1−10
Tsuda I (2001) Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav.
Brain Sci. 24: 793−810; discussions 811−847