Downloaded 88 times
![その他のIRL
31
IOC with Linearly-Solvable MDPs [Dvijotham 10]
モデルフリー，線形可解MDP
Deep IRL by Logistic Regression [Uchibe 16]
モデルフリー，線形可解MDP，非線形報酬関数
Generative Adversarial Imitation Learning [Ho 16]
モデルフリー，模倣学習，MaxEnt IRLと同じ方策
End-to-End Differentiable Adversarial Imitation Learning
[Baram 17]
状態遷移確率を学習し分散を減らすGAIL](https://image.slidesharecdn.com/maxdeeprelguided-170905142400/85/Maximum-Entropy-IRL-31-320.jpg)
![[DL輪読会]逆強化学習とGANs](https://cdn.slidesharecdn.com/ss_thumbnails/irlgans-171128063119-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]近年のオフライン強化学習のまとめ —Offline Reinforcement Learning: Tutorial, Review, an...](https://cdn.slidesharecdn.com/ss_thumbnails/20200626journalclubpub-200630064755-thumbnail.jpg?width=640&height=640&fit=bounds)
![SSII2021 [OS2-01] 転移学習の基礎：異なるタスクの知識を利用するための機械学習の方法](https://cdn.slidesharecdn.com/ss_thumbnails/os2-02final-210610091211-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Swin Transformer: Hierarchical Vision Transformer using Shifted Windows](https://cdn.slidesharecdn.com/ss_thumbnails/swintransformer-210514020542-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Understanding Black-box Predictions via Influence Functions](https://cdn.slidesharecdn.com/ss_thumbnails/dlhacksinffunc-170822055634-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Learning Robust Rewards with Adversarial Inverse Reinforcement Learning](https://cdn.slidesharecdn.com/ss_thumbnails/180201dllearningrobustrewardswithadversarial3-180205170610-thumbnail.jpg?width=640&height=640&fit=bounds)
![[Dl輪読会]introduction of reinforcement learning](https://cdn.slidesharecdn.com/ss_thumbnails/dlintroductionofreinforcementlearning-161121061444-thumbnail.jpg?width=640&height=640&fit=bounds)
Maximum Entropy IRL（最大エントロピー逆強化学習）とその発展系について
- 1.
- 2. 発表の内容 はじめに 2 逆強化学習ににおける三つの課題を扱う． 1. エキスパートが訪れていない状態の報酬を推定 • 報酬の関数近似 2.解の曖昧さへの対処（凸最適化問題として定式化） • 最大エントロピーの原理による定式化(Maximum Entropy IRL) • 相対エントロピー最小化による定式化(Relative Entropy IRL) 3. 試行錯誤の削減 • 重要サンプリングで報酬の更新式に含まれる分配関数を推定
- 3. 発表の構成 はじめに 3 1. IRLによる報酬関数の推定 • 線形関数の推定 •非線形関数の推定 2. 最大エントロピーの原理による解の曖昧さへの対処 • Maximum Entropy IRL(線形関数) • Maximum Entropy Deep IRL(非線形関数) 3. 重要サンプリングによる分配関数Z(θ)の推定 • Relative Entropy IRL(線形関数，相対エントロピー最小化) • Guided Cost Learning(非線形関数，Maximum Entropy)
- 4.
- 5. 逆強化学習(IRL) 1. IRLによる報酬関数の推定 5 目的 エキスパートの意思決定系列を所与として エキスパートの方策が最適方策となる報酬rを推定 Input Output Expert’s reward 報酬以外の環境の情報 エキスパートの意思決定系列（軌跡） エキスパートの報酬関数 ある報酬の元で最適なエージェント
- 6. 報酬関数の推定 1. IRLによる報酬関数の推定 6 1. 全状態でのエキスパートの情報が得られないことも． 2.一部の状態の情報を元に全状態の報酬を推定したい． 3. 報酬を関数近似し全状態での報酬を推定．
- 7. 報酬関数の推定 1. IRLによる報酬関数の推定 7 𝑘個の特徴量を持つ特徴ベクトル𝜙 = 𝜙1, … , 𝜙 𝑘 ⊤ 𝜙: 𝑆 → ℝ 𝑘 状態空間を𝑘次元実数空間に写像 特徴量は速度や座標など状態を表す情報 特徴ベクトルが近い状態は報酬も近いと仮定 報酬r を特徴ベクトルとパラメータの関数で表す．
- 8. Function Limit Linear Nonlinear× BNP-FIRL Only Piecewise constant functions GPIRL Computational complexity Neural Net 報酬関数の例 1. IRLによる報酬関数の推定 8
- 9.
- 10. 推定した報酬が満たすべき条件(線形） 1. IRLによる報酬関数の推定 10 最適方策が エキスパートの方策となる報酬を推定 推定した報酬の元での最適方策は次の条件を満たす． • と の報酬の期待値が一致 • と の特徴期待ベクトルが一致 上式を満たす軌跡の分布になる報酬を見つければ良い． しかし，上式満たす軌跡の分布は複数存在する．（報酬も複数） どのような軌跡の分布が良いだろうか？
- 11.
- 12. Maximum Entropy IRL 2.最大エントロピーの原理による解の曖昧さへの対処 12 条件1:特徴期待値が一致 条件2, 3 :Pは確率 条件4 : 軌跡は離散 エントロピー最大化 意味 数式
- 13. Maximum Entropy IRL 2.最大エントロピーの原理による解の曖昧さへの対処 13 ラグランジュの未定乗数法で解くと次式が得られる． 軌跡が得られる確率は報酬の大きさに指数比例 この式に基づき に対して尤度最大化
- 14. Maximum Entropy IRL 2.最大エントロピーの原理による解の曖昧さへの対処 14 対数尤度を勾配法で最大化 エキスパートと比較して 特徴期待値：小 → 重み：大きく更新 特徴期待値：大 → 重み：小さく更新 勾配の意味
- 15. Maximum Entropy IRL 2.最大エントロピーの原理による解の曖昧さへの対処 15 勾配の計算方法 : から計算 : を更新するごとにDP or RLを行い計算
- 16. Deep Maximum EntropyIRL 2. 最大エントロピーの原理による解の曖昧さへの対処 16 対数尤度を勾配法で最大化 エキスパートと比較して 状態を訪れる頻度：小 → 重み：報酬を大きく更新 状態を訪れる頻度：大 → 重み：報酬を小さく更新 勾配の意味 エキスパートが状態を訪れる頻度 θの元で状態を訪れる頻度
- 17. Deep Maximum EntropyIRL 2. 最大エントロピーの原理による解の曖昧さへの対処 17 勾配の計算方法 : から計算 : を更新するごとにDP or RLを行い計算
- 18. Deep Maximum EntropyIRL 2. 最大エントロピーの原理による解の曖昧さへの対処 18 勾配の計算方法 : から計算 : を更新するごとにDP or RLを行い計算 めちゃくちゃ大変！！！！！！
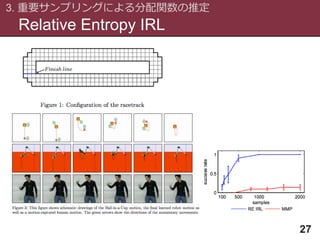
- 19. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 19 DPやRLが必要なのは下の二つを計算したいから． θに対する最適方策を使わずに上式を求めたい 最適方策が必要なければ試行錯誤が格段に減る！！ 少し異なる問題設定を考える．
- 20. エキスパートの軌跡の分布 との相対エントロピーを最小化 Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 20 条件1:特徴期待値が一致 条件2, 3 :Pは確率 条件4 : 軌跡は離散 意味 数式 ※簡単のためMaxEntに合わせて条件1を改変
- 21. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 21 ラグランジュの未定乗数法で解くと次式が得られる． 軌跡が得られる確率： に指数比例， に比例 この式に基づき に対して尤度最大化
- 22. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 22 Relative Entropy IRL Maximum Entropy IRL
- 23. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 23 Zさえ近似できれば計算できる． ※Q(ζ)が求まるかはここでは考えない 重要サンプリングを用いれば上式も求まる．
- 24. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 24 重要サンプリングを使う
- 25. ※ここでの はエキスパートの軌跡を元にした結合確率 Relative EntropyIRL 3. 重要サンプリングによる分配関数の推定 25 ある軌跡が得られる確率 = 初期状態分布×方策×状態遷移確率×方策．．． H : 軌跡のステップ数
- 26. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 26 同じ環境で試行錯誤している→状態遷移確率が同じなので打ち消しあう Zが求まる！！！ ・軌跡をサンプリングする方策はランダム方策でも良い. ・報酬を更新する毎に最適方策を求める必要もない． ・状態遷移確率が分からなくても良い（モデルフリー）
- 27. Relative Entropy IRL 3.重要サンプリングによる分配関数の推定 27
- 28. Guided Cost Learning 3.重要サンプリングによる分配関数の推定 28 Maximum Entropy IRLの問題設定でZを近似 Relative Entropy IRLでは状態遷移確率が消えた Maximum Entropy IRLでは状態遷移確率が消えない 状態遷移確率を近似してP(ζ)を求める
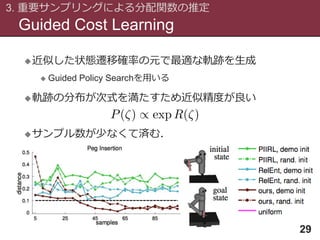
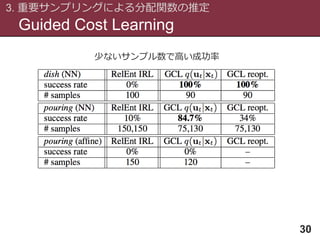
- 29. Guided Cost Learning 3.重要サンプリングによる分配関数の推定 29 近似した状態遷移確率の元で最適な軌跡を生成 Guided Policy Searchを用いる 軌跡の分布が次式を満たすため近似精度が良い サンプル数が少なくて済む．
- 30. Guided Cost Learning 3.重要サンプリングによる分配関数の推定 30 少ないサンプル数で高い成功率
- 31. その他のIRL 31 IOC with Linearly-SolvableMDPs [Dvijotham 10] モデルフリー，線形可解MDP Deep IRL by Logistic Regression [Uchibe 16] モデルフリー，線形可解MDP，非線形報酬関数 Generative Adversarial Imitation Learning [Ho 16] モデルフリー，模倣学習，MaxEnt IRLと同じ方策 End-to-End Differentiable Adversarial Imitation Learning [Baram 17] 状態遷移確率を学習し分散を減らすGAIL
- 32. 1. 2. 3.4. 5. 32
Editor's Notes
- #11 質問