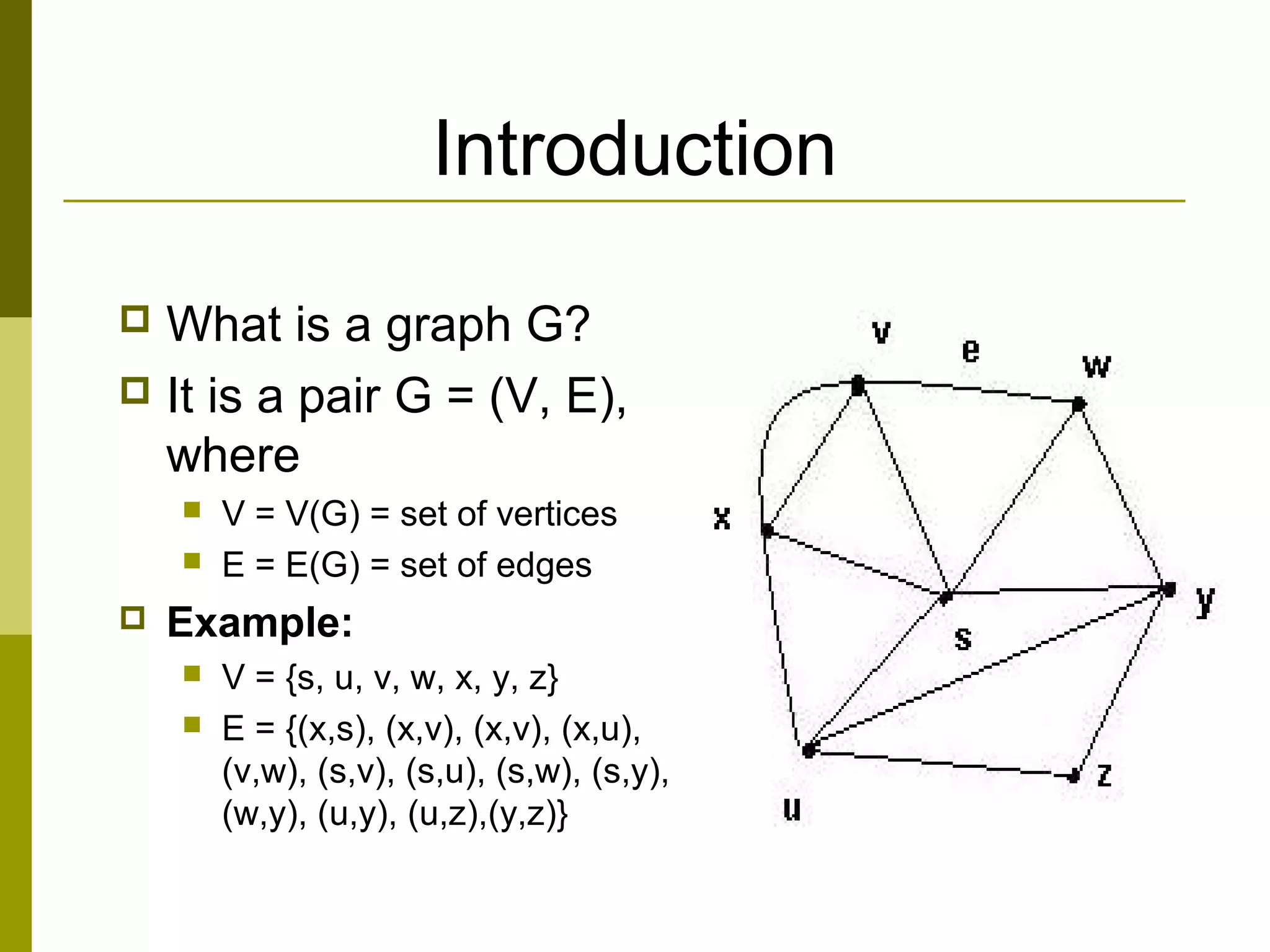
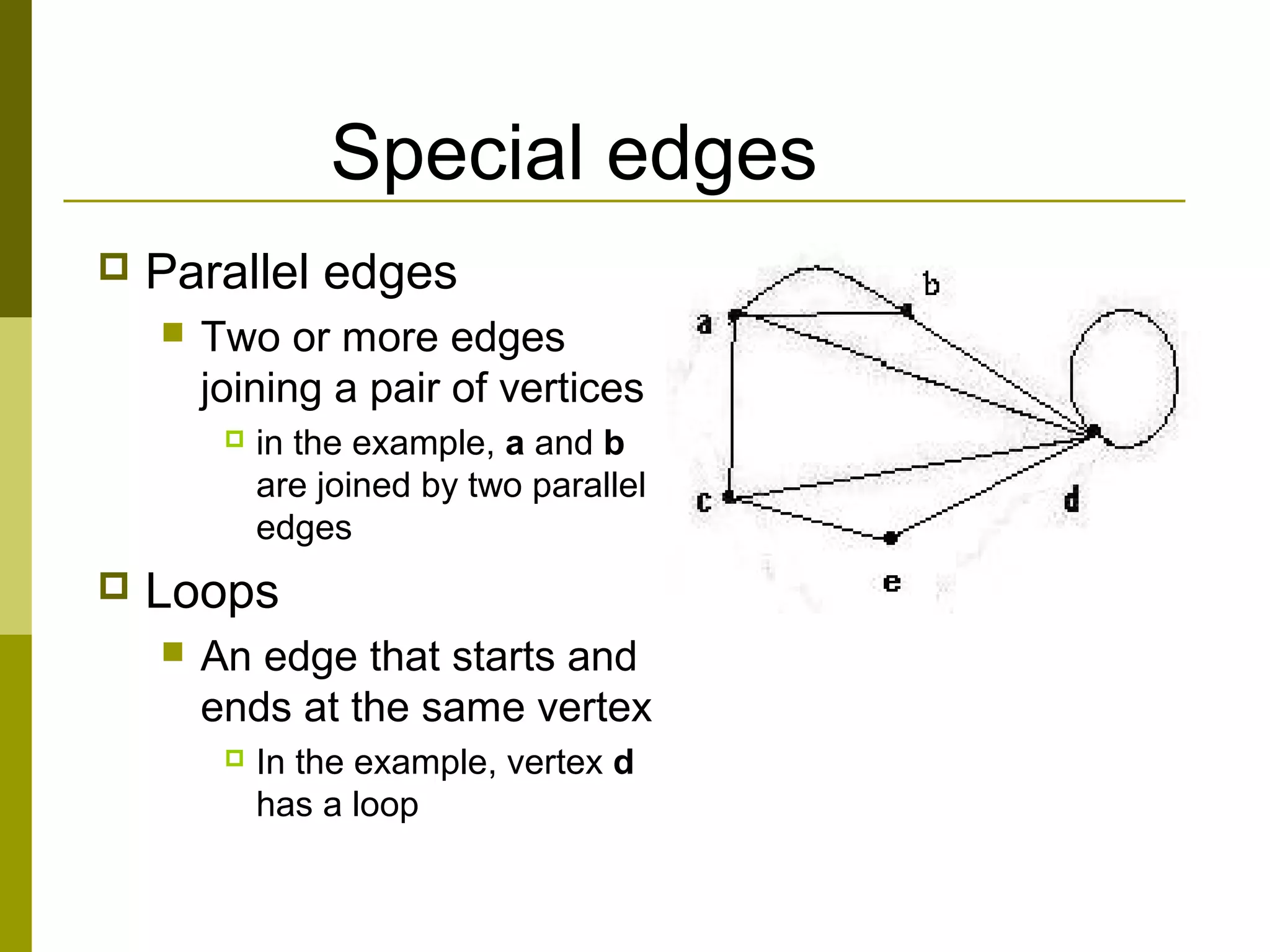
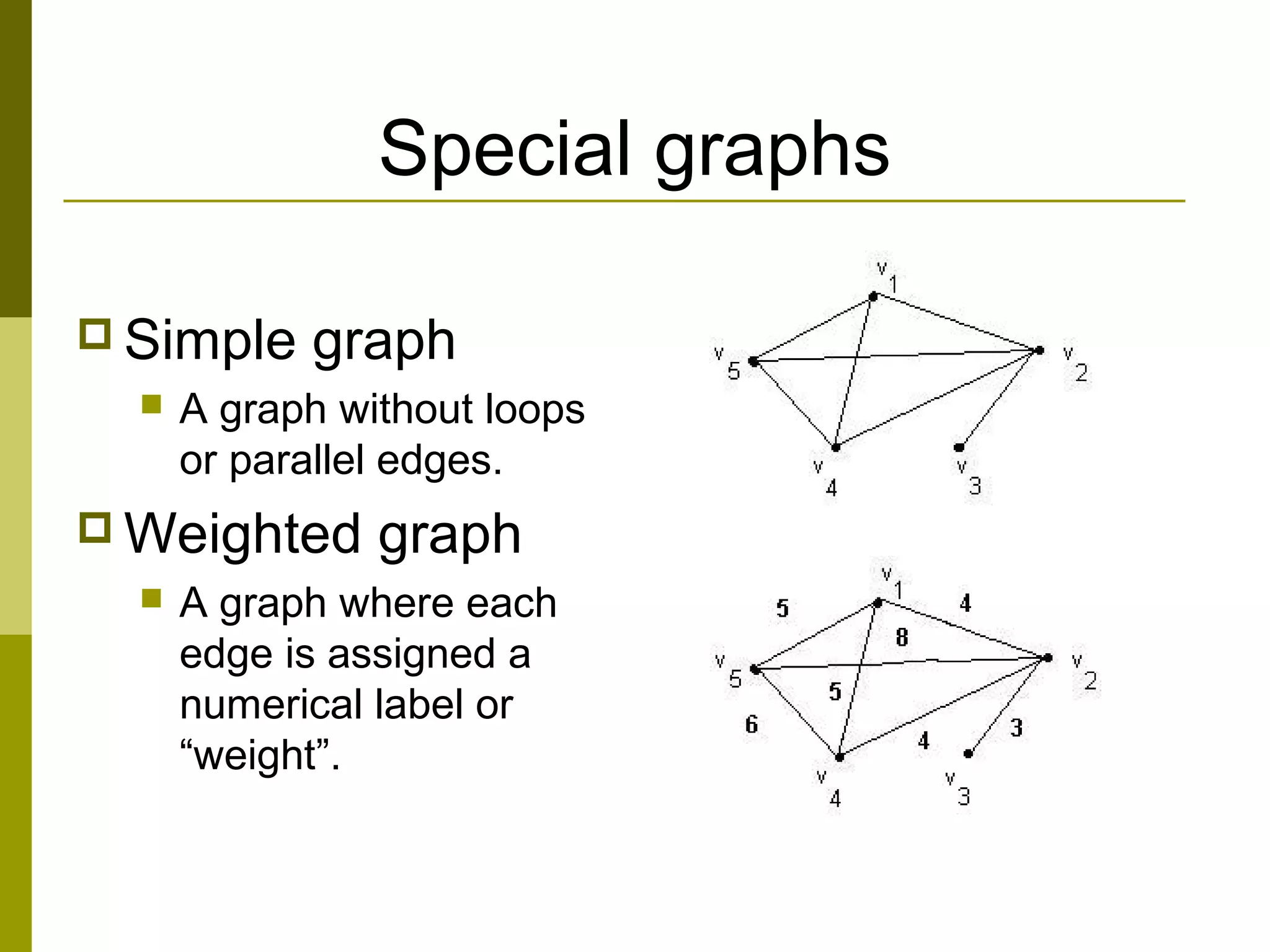
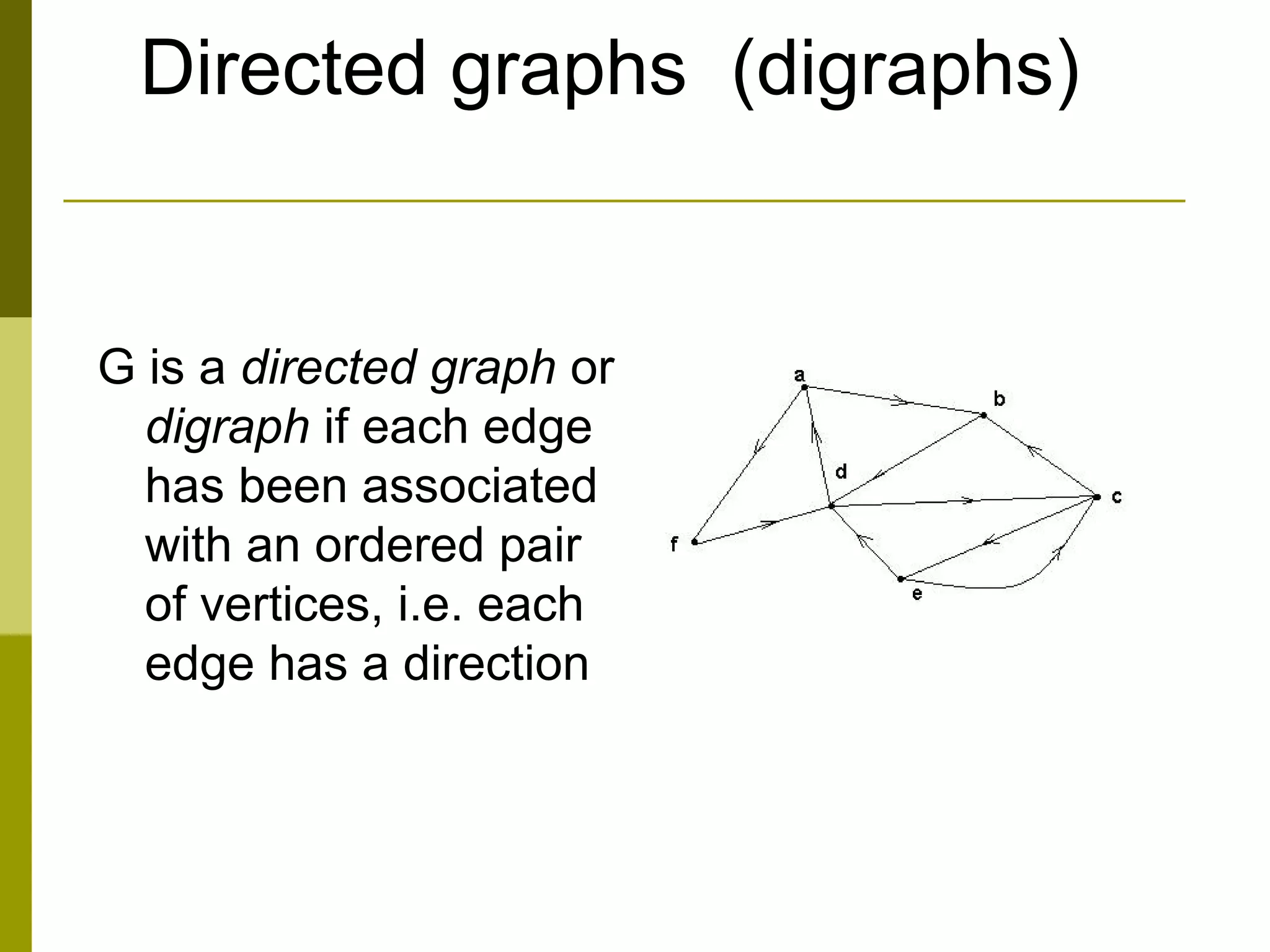
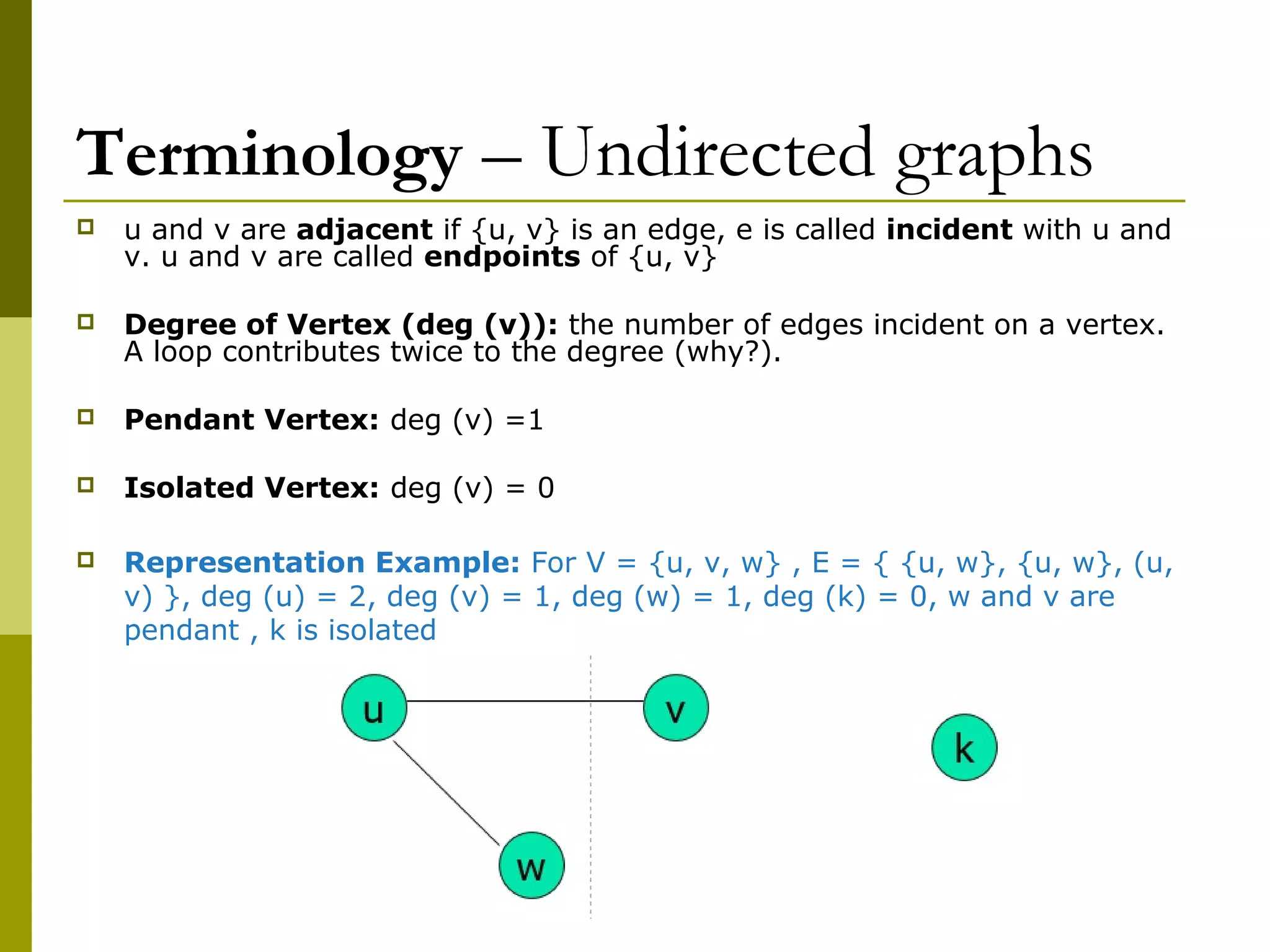
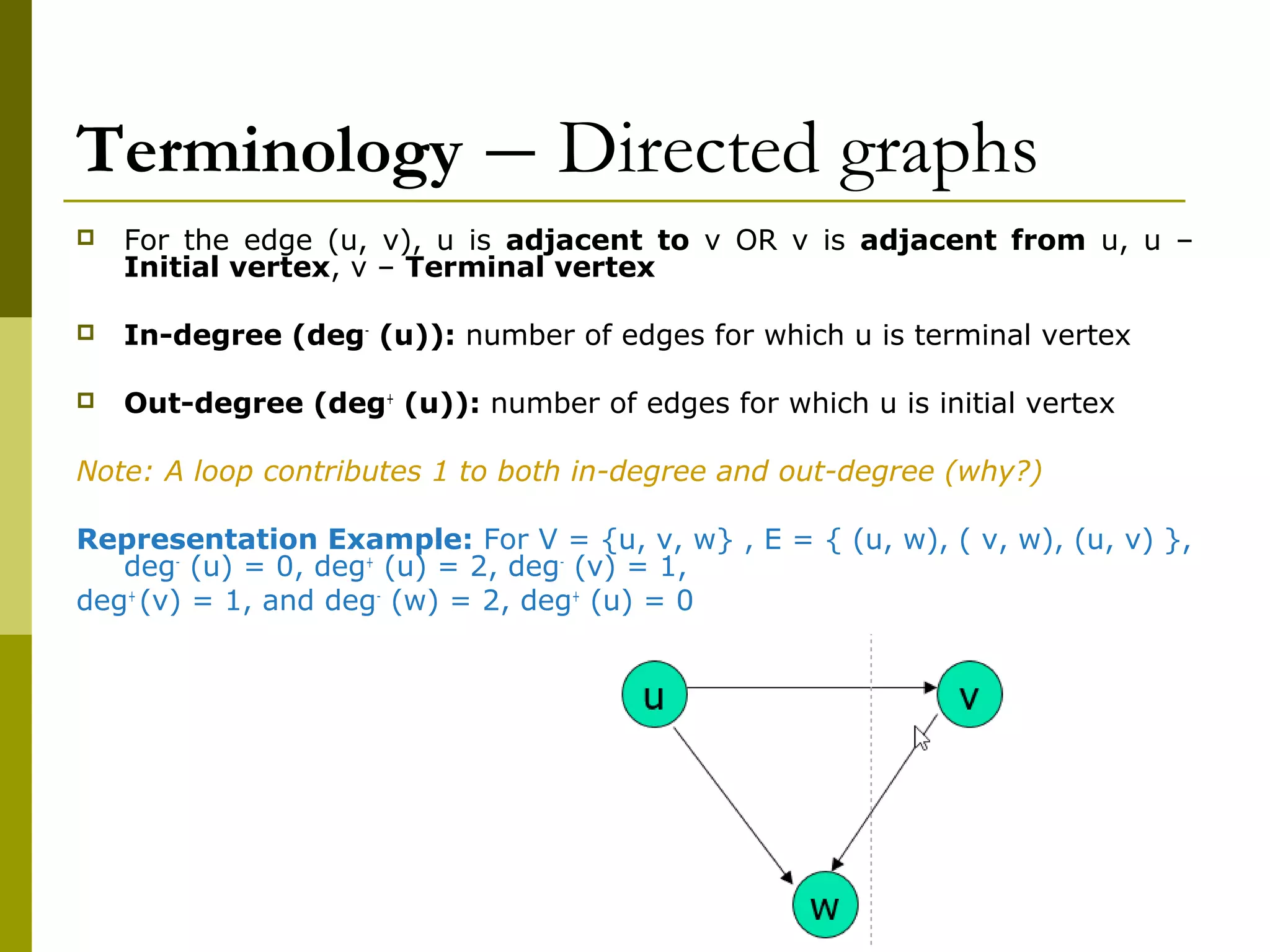
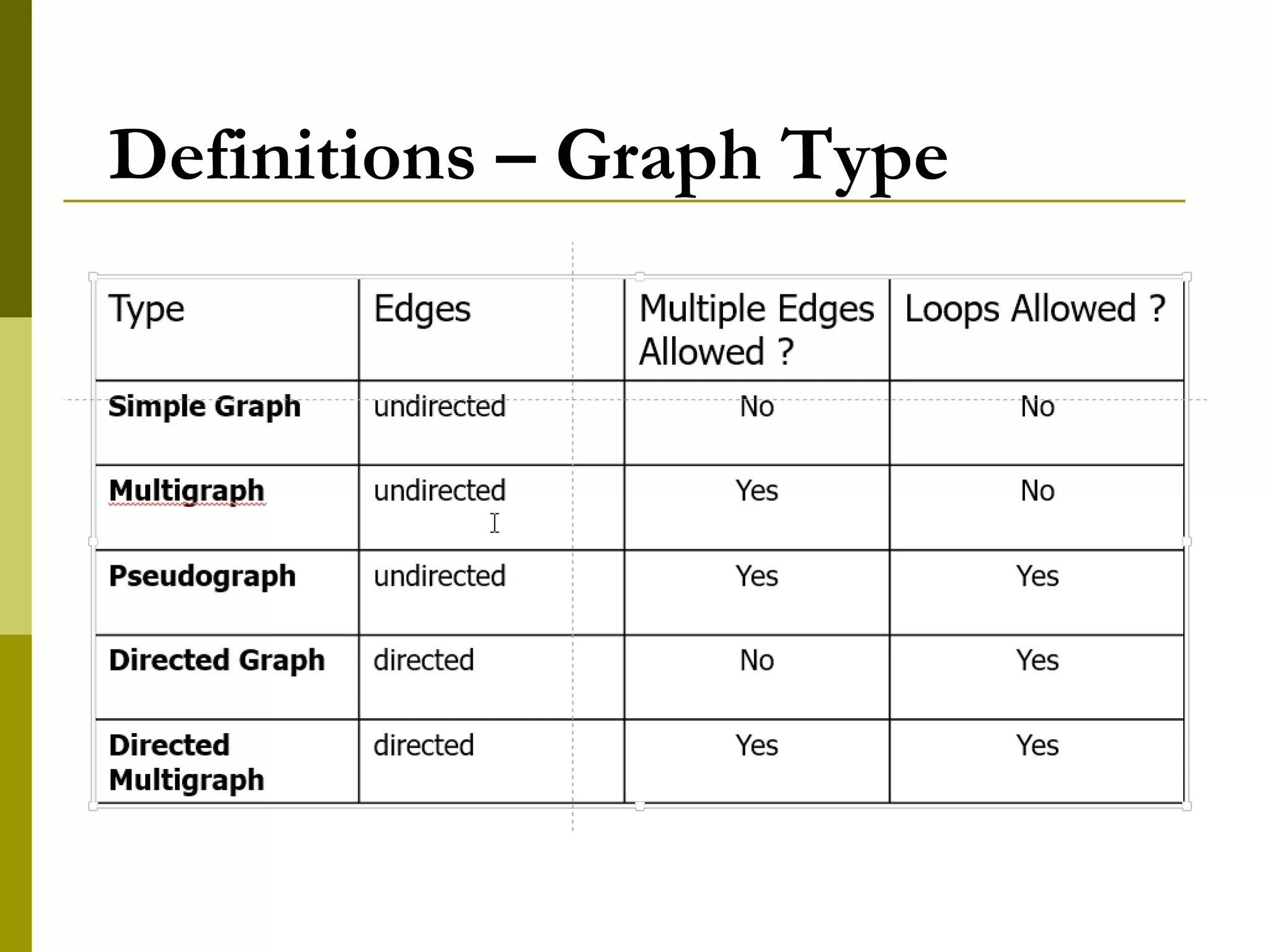
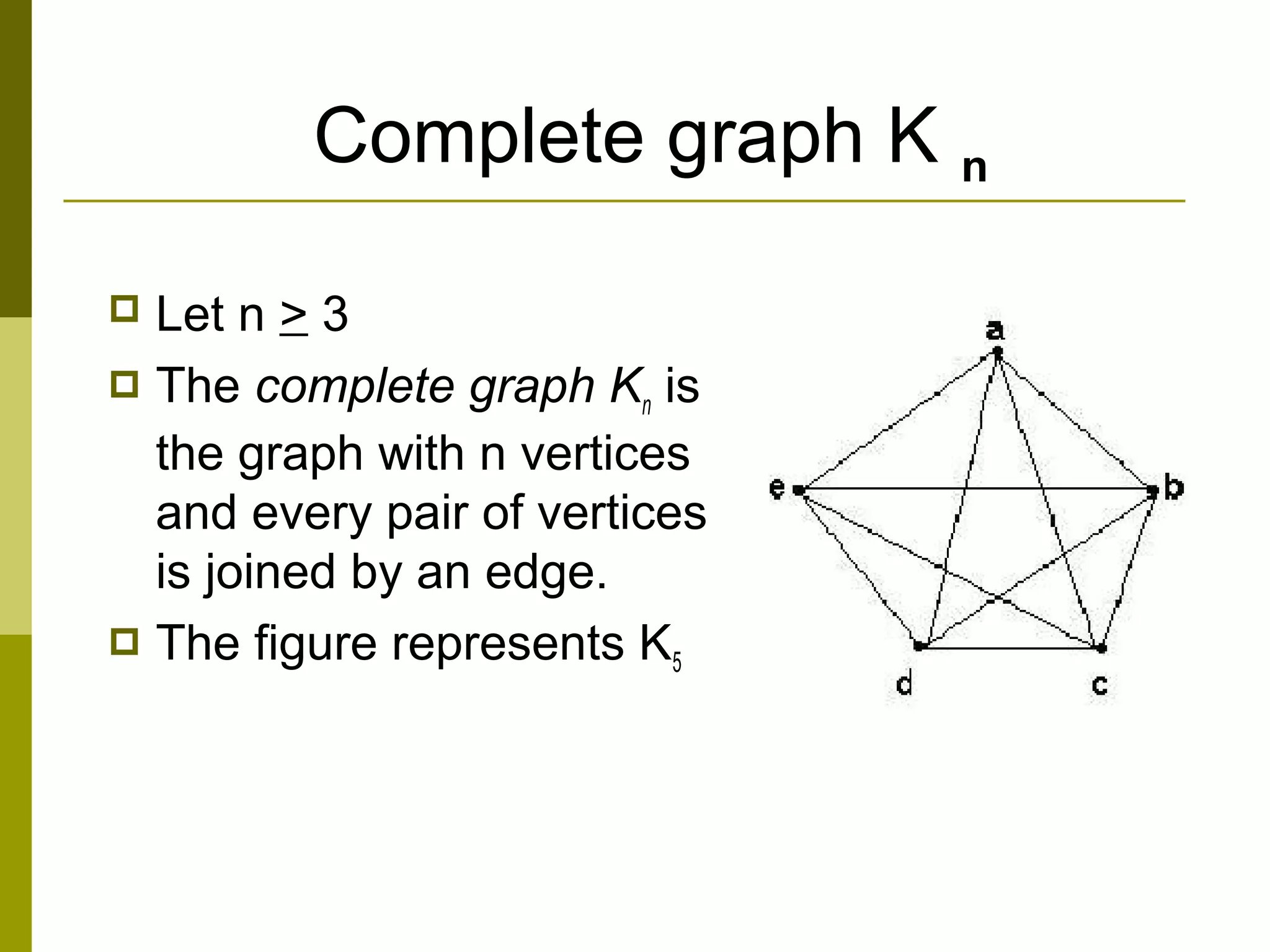
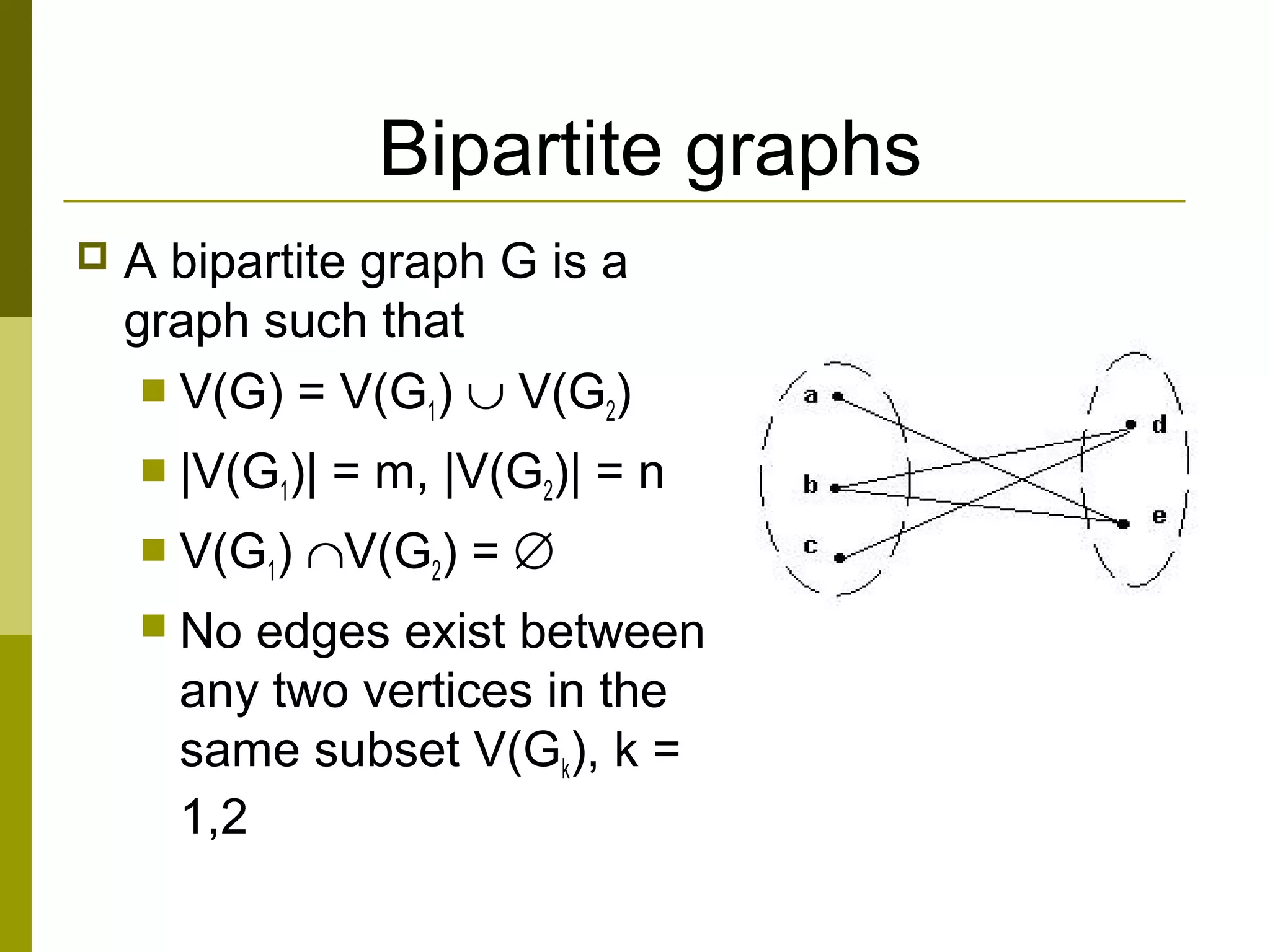
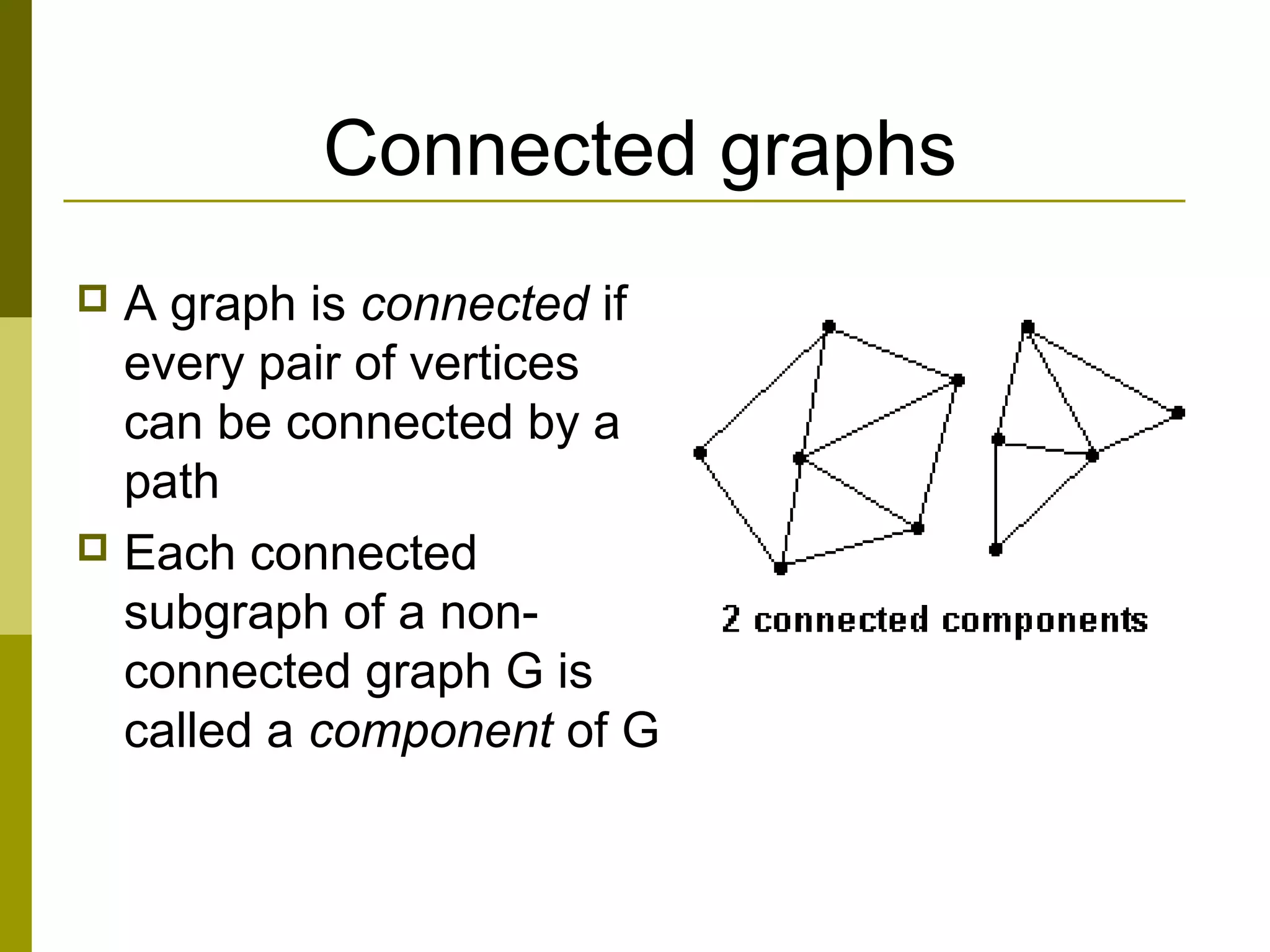
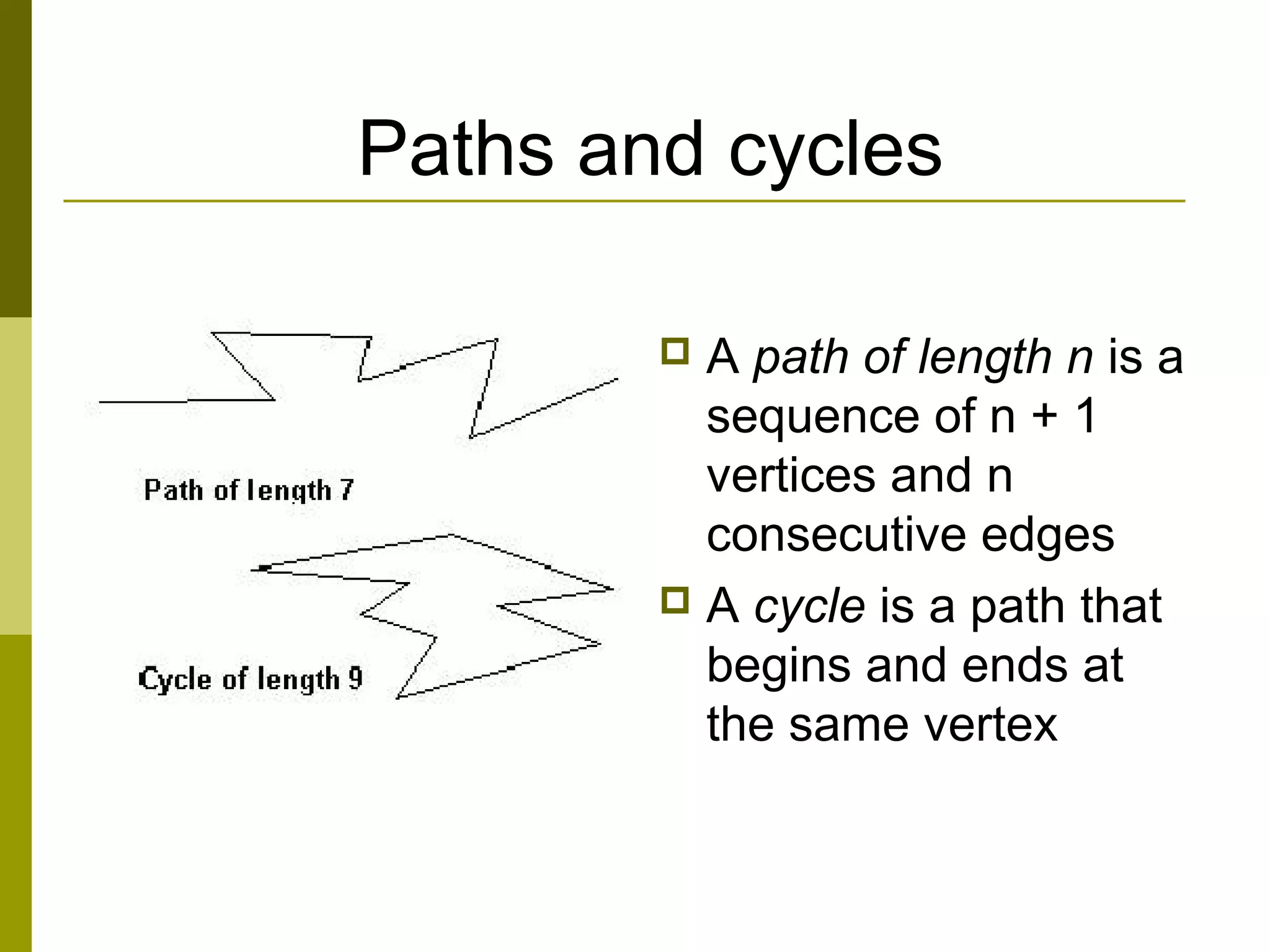
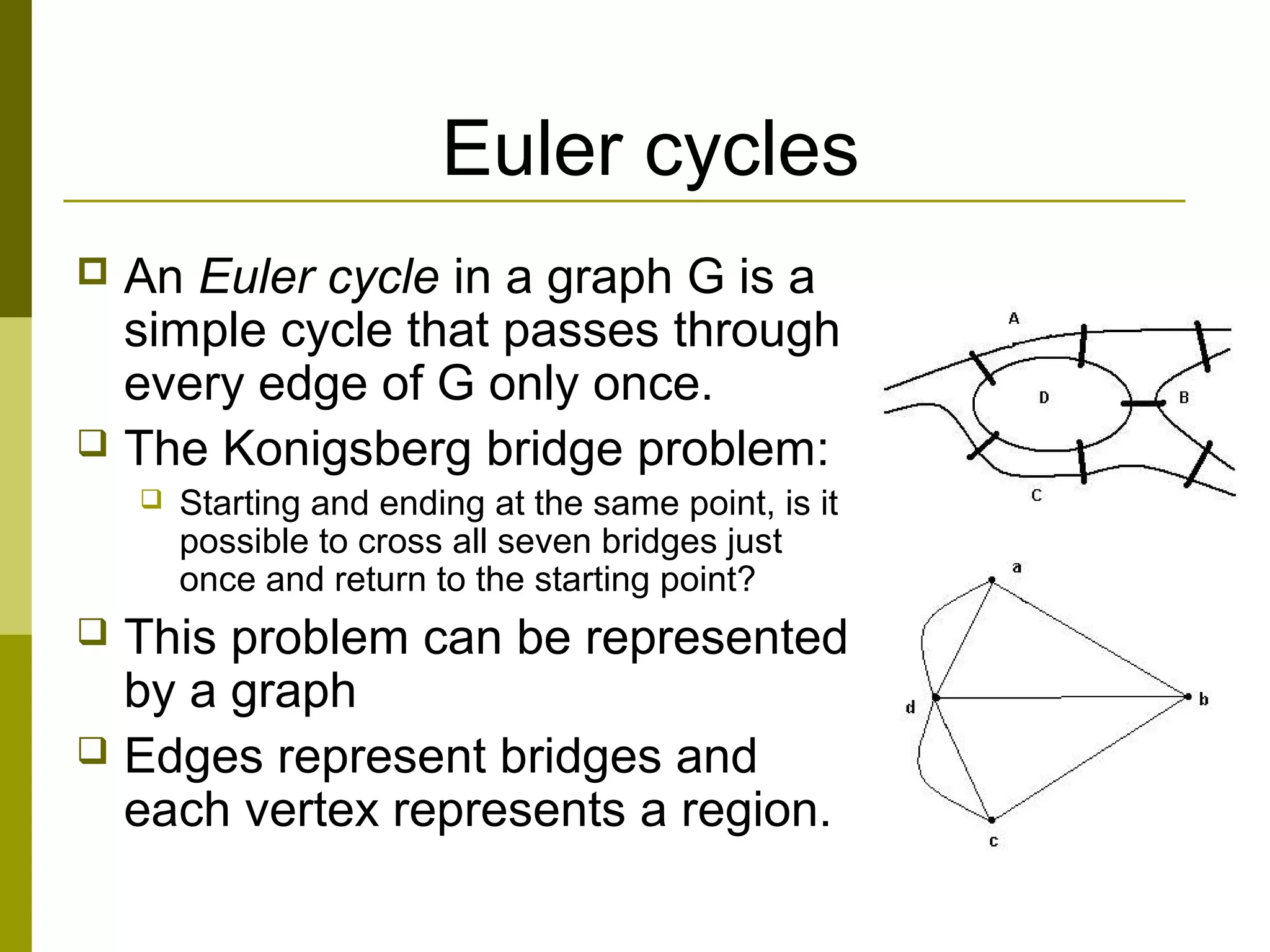
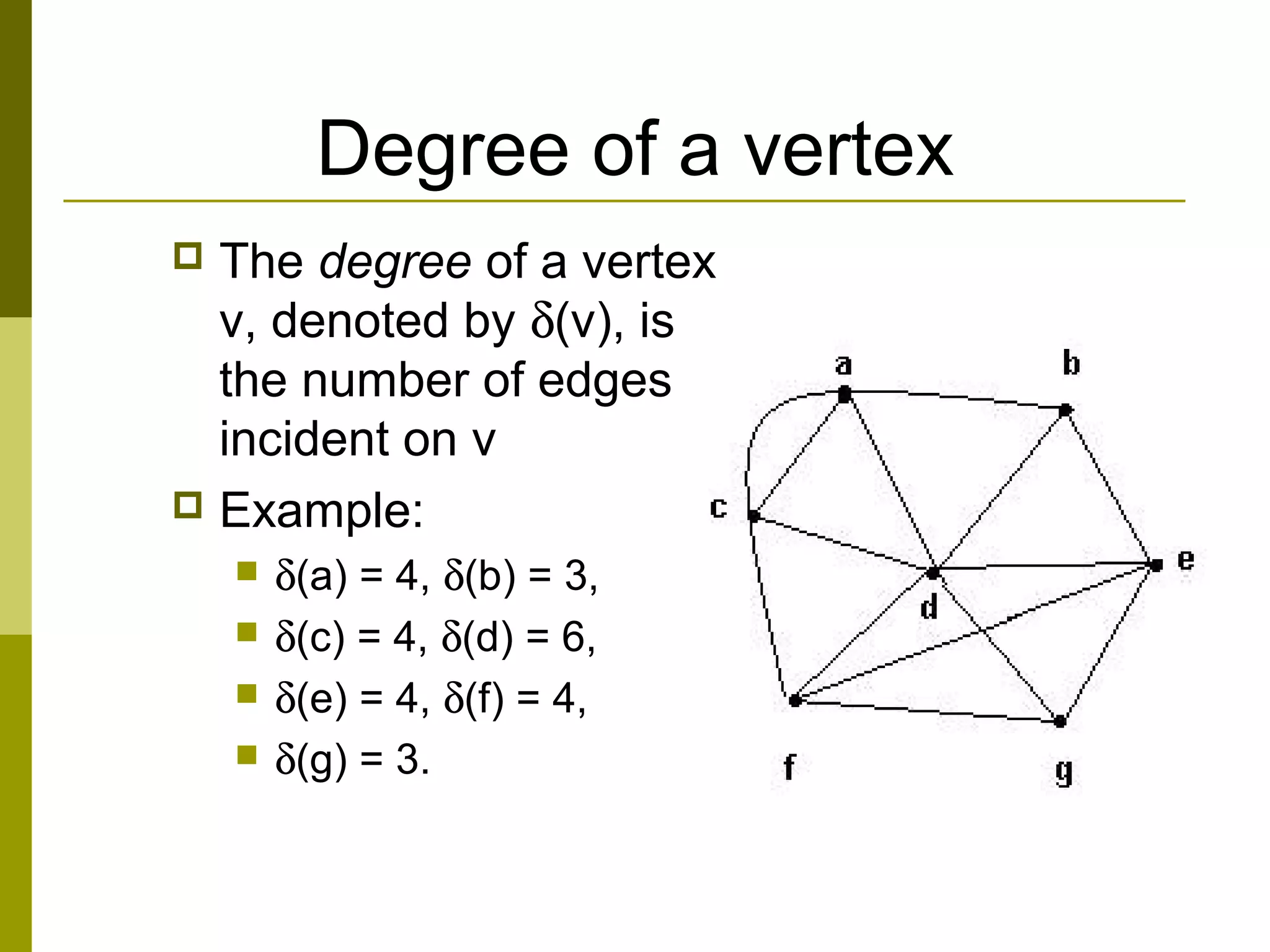
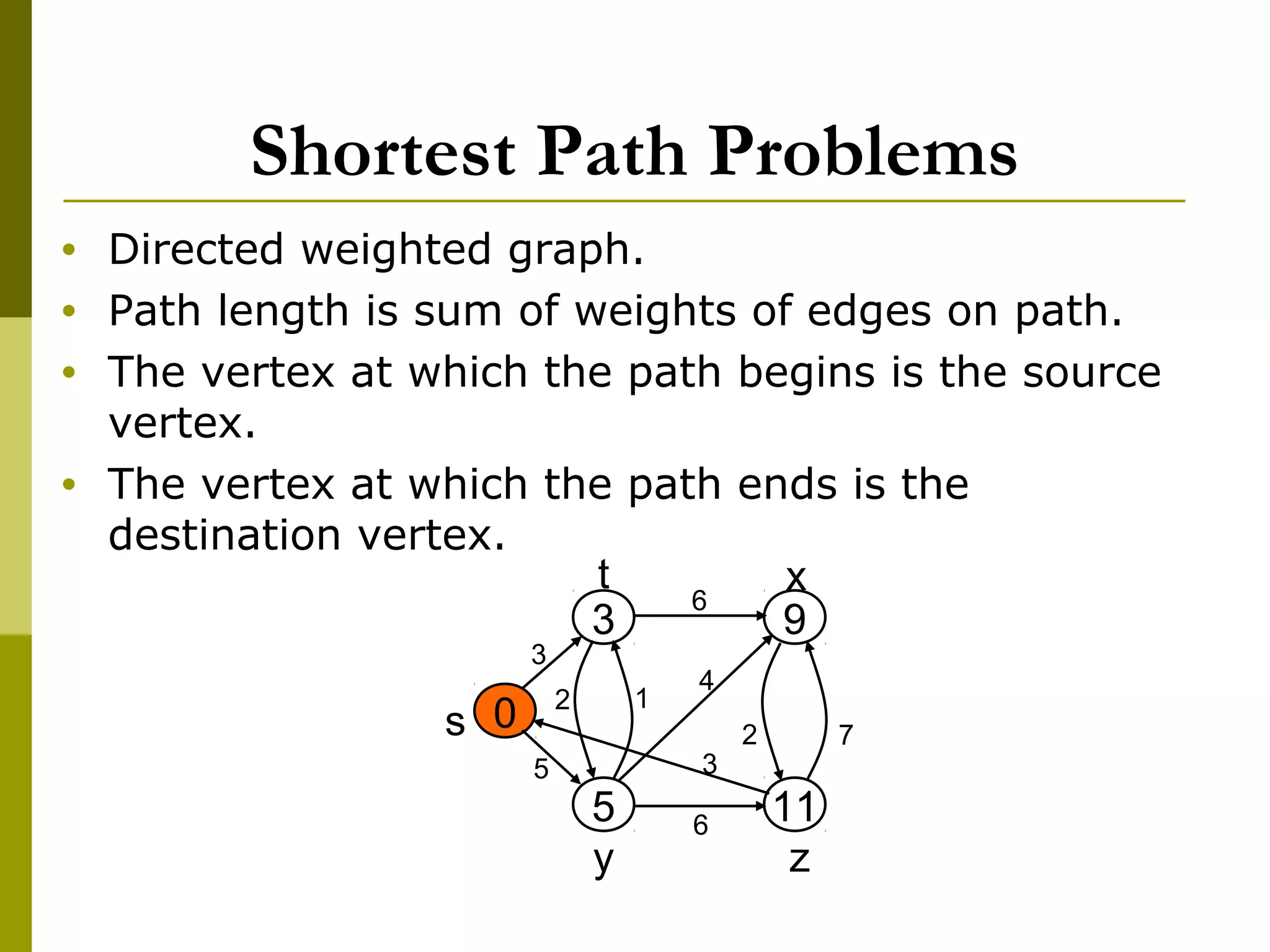
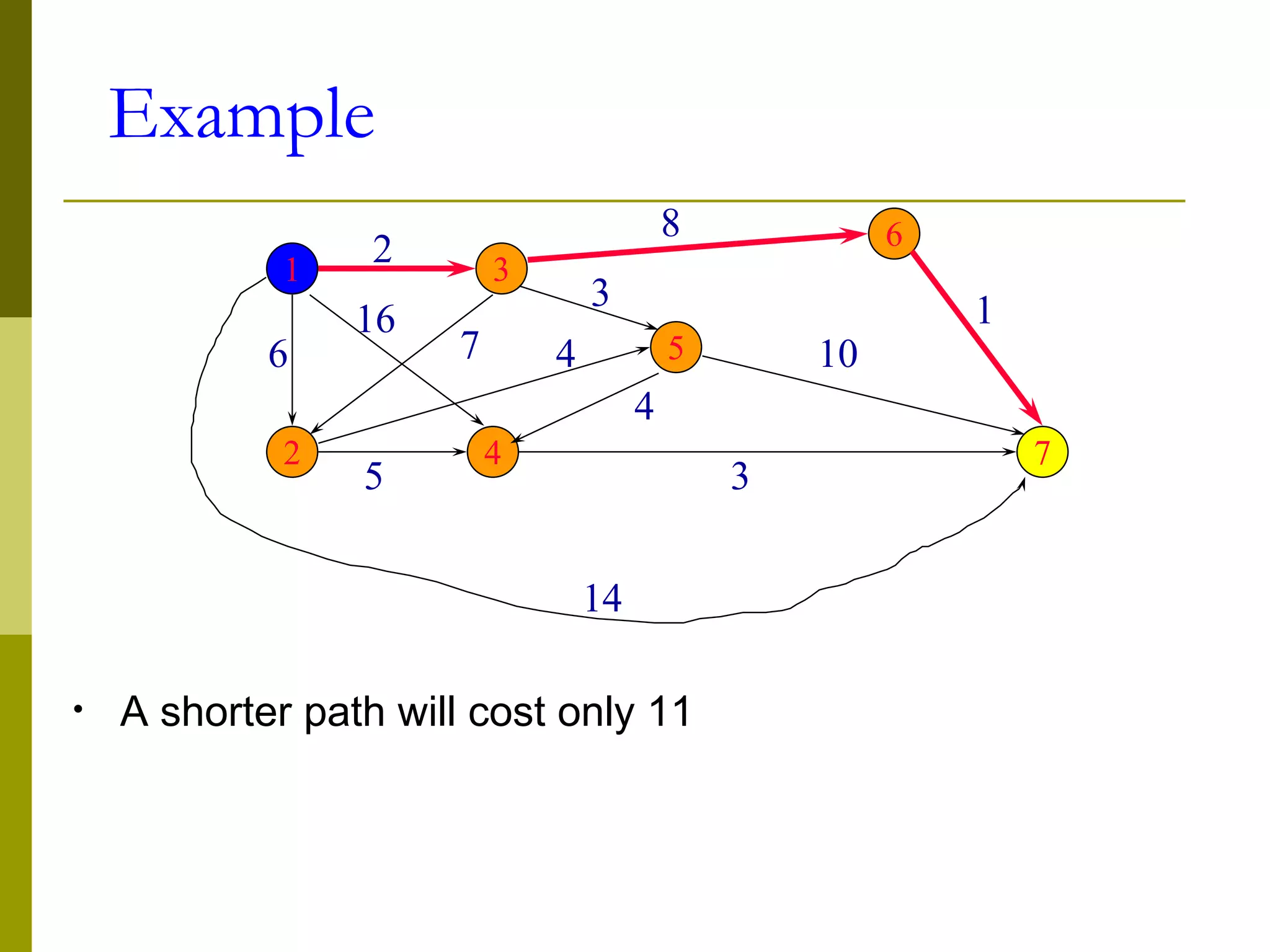
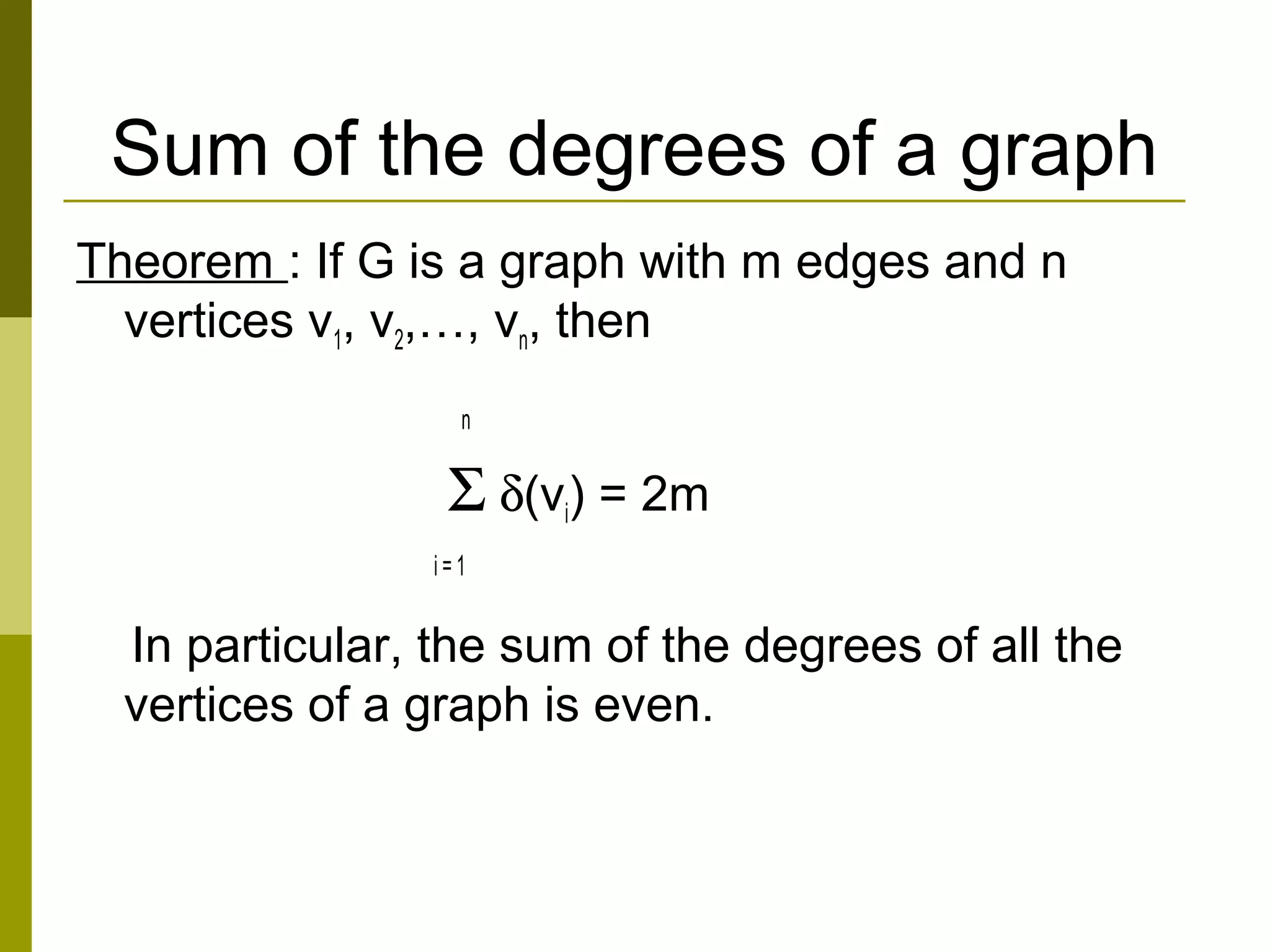The document provides an introduction to graph theory, defining key concepts such as graphs, vertices, edges, and types of graphs including directed, undirected, weighted, and bipartite graphs. It also explores special properties, theorems, and terminologies related to graph degree, connectivity, paths, cycles, and representations of graphs. Additionally, it discusses applications such as Euler cycles and shortest path problems.

1. Welcome to Discrete Mathematics
PRESENTATION
Topics: Graph Theory
Submited by:
Md: Aliul Kadir akib
Daffodil International University
Mail:aliulkadir@gmail.com

2. Introduction
 What is a graph G?
 It is a pair G = (V, E),
where
 V = V(G) = set of vertices
 E = E(G) = set of edges
 Example:
 V = {s, u, v, w, x, y, z}
 E = {(x,s), (x,v), (x,v), (x,u),
(v,w), (s,v), (s,u), (s,w), (s,y),
(w,y), (u,y), (u,z),(y,z)}

3. Special edges
 Parallel edges
 Two or more edges
joining a pair of vertices
 in the example, a and b
are joined by two parallel
edges
 Loops
 An edge that starts and
ends at the same vertex
 In the example, vertex d
has a loop

4. Special graphs
 Simple graph
 A graph without loops
or parallel edges.
 Weighted graph
 A graph where each
edge is assigned a
numerical label or
“weight”.

5. Directed graphs (digraphs)
G is a directed graph or
digraph if each edge
has been associated
with an ordered pair
of vertices, i.e. each
edge has a direction

6. Terminology – Undirected graphs
 u and v are adjacent if {u, v} is an edge, e is called incident with u and
v. u and v are called endpoints of {u, v}
 Degree of Vertex (deg (v)): the number of edges incident on a vertex.
A loop contributes twice to the degree (why?).
 Pendant Vertex: deg (v) =1
 Isolated Vertex: deg (v) = 0
 Representation Example: For V = {u, v, w} , E = { {u, w}, {u, w}, (u,
v) }, deg (u) = 2, deg (v) = 1, deg (w) = 1, deg (k) = 0, w and v are
pendant , k is isolated

7. Terminology – Directed graphs
 For the edge (u, v), u is adjacent to v OR v is adjacent from u, u –
Initial vertex, v – Terminal vertex
 In-degree (deg-
(u)): number of edges for which u is terminal vertex
 Out-degree (deg+
(u)): number of edges for which u is initial vertex
Note: A loop contributes 1 to both in-degree and out-degree (why?)
Representation Example: For V = {u, v, w} , E = { (u, w), ( v, w), (u, v) },
deg-
(u) = 0, deg+
(u) = 2, deg-
(v) = 1,
deg+
(v) = 1, and deg-
(w) = 2, deg+
(u) = 0

8. Theorems: Undirected Graphs
Theorem 1
The Handshaking theorem:
(why?) Every edge connects 2 vertices
∑∈
=
Vv
ve2

9. Theorems: Undirected Graphs
Theorem 2:
An undirected graph has even number of vertices
with odd degree
even
Voof
=⇒
⇒
⇒
∈⇒
+==
∑
∑∑∑
∈
∈∈∈
2
21
Vv
1,
VvVuVv
deg(v)termsecond
evenalsoistermsecondHence
2e.issumsinceevenisinequalitylastthe
ofsidehandrighton thetermslast twotheofsumThe
even.isinequalitylasttheofsidehandrightin thefirst termThe
Vfor vevenis(v)deg
deg(v)deg(u)deg(v)2e
verticesdegreeoddtorefersV2andverticesdegreeevenofsettheis1Pr

10. Definitions – Graph Type

11. Simple graphs – special cases
 Wheels: Wn, obtained by adding additional
vertex to Cn and connecting all vertices to
this new vertex by new edges.
Representation Example: W3, W4

12. Complete graph K n
 Let n > 3
 The complete graph Kn is
the graph with n vertices
and every pair of vertices
is joined by an edge.
 The figure represents K5

13. Bipartite graphs
 A bipartite graph G is a
graph such that
 V(G) = V(G1) ∪ V(G2)
 |V(G1)| = m, |V(G2)| = n
 V(G1) ∩V(G2) = ∅
 No edges exist between
any two vertices in the
same subset V(Gk), k =
1,2

14. Complete bipartite graph Km,n
 A bipartite graph is the
complete bipartite graph Km,n if
every vertex in V(G1) is joined
to a vertex in V(G2) and
conversely,
 |V(G1)| = m
 |V(G2)| = n

15. Connected graphs
 A graph is connected if
every pair of vertices
can be connected by a
path
 Each connected
subgraph of a non-
connected graph G is
called a component of G

16. Paths and cycles
 A path of length n is a
sequence of n + 1
vertices and n
consecutive edges
 A cycle is a path that
begins and ends at
the same vertex

17. Euler cycles
 An Euler cycle in a graph G is a
simple cycle that passes through
every edge of G only once.
 The Konigsberg bridge problem:
 Starting and ending at the same point, is it
possible to cross all seven bridges just
once and return to the starting point?
 This problem can be represented
by a graph
 Edges represent bridges and
each vertex represents a region.

18. Degree of a vertex
 The degree of a vertex
v, denoted by δ(v), is
the number of edges
incident on v
 Example:
 δ(a) = 4, δ(b) = 3,
 δ(c) = 4, δ(d) = 6,
 δ(e) = 4, δ(f) = 4,
 δ(g) = 3.

19. Sum of the degrees of a graph
Theorem : If G is a graph with m edges and n
vertices v1, v2,…, vn, then
n
Σ δ(vi) = 2m
i = 1
In particular, the sum of the degrees of all the
vertices of a graph is even.

20. Shortest Path Problems
• Directed weighted graph.
• Path length is sum of weights of edges on path.
• The vertex at which the path begins is the source
vertex.
• The vertex at which the path ends is the
destination vertex.
0
3 9
5 11
3
6
5
7
6
s
t x
y z
2
2 1
4
3

21. Example
1
2
3
4
5
6
7
2
6
16
7
8
10
3
14
4
4
5 3
1
• A shorter path will cost only 11

22. Representations of graphs
 Adjacency matrix
Rows and columns are
labeled with ordered
vertices
write a 1 if there is an edge
between the row vertex
and the column vertex
and 0 if no edge exists
between them
v w x y
v 0 1 0 1
w 1 0 1 1
x 0 1 0 1
y 1 1 1 0

23. Euler’s formula
 If G is planar graph,
 v = number of vertices
 e = number of edges
 f = number of faces,
including the exterior face
 Then: v – e + f = 2