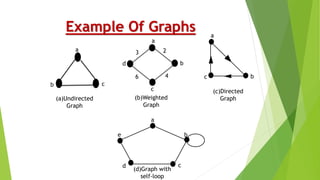
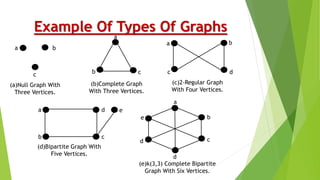
Graph theory is the study of points and lines, and how sets of points called vertices can be connected by lines called edges. It involves types of graphs like regular graphs where each vertex has the same number of neighbors, and bipartite graphs where the vertices can be partitioned into two sets with no edges within each set. Graphs can be represented using adjacency matrices and adjacency lists. Basic graph algorithms include depth-first search, breadth-first search, and finding shortest paths between vertices. Graph coloring assigns colors to vertices so that no adjacent vertices have the same color.

1. GRAPH THEORY
DISCRETE MATHEMATICS

2. Introduction
 Graph Theory is the study of points and lines.
 In particular, it involves the ways in which sets of
points, called vertices, can be connected by lines
called edges.
 Graph Theory has proven useful in the design of
integrated circuits for computers and other
electronic devices.
 Graph Theory was invented by Leonhard Euler.

3. Graphs And Basic Terminologies
 A Graph is an ordered pair G = (V, E) comprising
a set V of vertices, nodes or points together with a
set E of edges, arcs or lines, which are 2-element subsets
of V.
 An edge is associated with two vertices, and the
association takes the form of the unordered pair of the
vertices.
 A Graph may be directed or undirected, weighted or
unweighted.
 A Graph may be with self-loop or self-edge.

4. Example Of Graphs
(a)Undirected
Graph
a
b
c
d
a
b c
3 2
6 4
(b)Weighted
Graph
a
bc
(c)Directed
Graph
(d)Graph with
self-loop
a
be
cd

5. Types Of Graphs
Null Graph:
 A Graph which contains only isolated nodes(i.e. set of edges of graph
is empty) is called as Null Graph.
Regular Graph:
 A Graph in which each vertex has the same number of neighbours(i.e.
every vertex has the same degree) is called as Regular Graph.
 A Regular Graph with vertices of degree K is called a K -Regular
Graph or regular graph of degree K.
Complete Graph:
 A Complete Graph is a graph in which each pair of vertices is joined
by an edge.
 A Complete Graph contains all possible edges.

6. Types Of Graphs
Bipartite Graph:
 A Bipartite Graph is a graph in which the vertex set can
be partitioned into two sets, W and X, so that no two vertices
in W share a common edge and no two vertices in X share a common
edge.
 Chromatic number of Bipartite Graph is 2.
Complete Bipartite Graph:
 In a Complete Bipartite Graph, the vertex set is the union of two
disjoint sets, W and X, so that every vertex in W is adjacent to every
vertex in X but there are no edges within W or X.

7. Example Of Types Of Graphs
(a)Null Graph With
Three Vertices.
a b
c
(b)Complete Graph
With Three Vertices.
a b
cc db
a
(c)2-Regular Graph
With Four Vertices.
a
b c
ed
(d)Bipartite Graph With
Five Vertices.
a
b
c
d
d
e
(e)k(3,3) Complete Bipartite
Graph With Six Vertices.

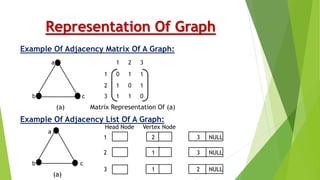
8. Representation Of Graph
Two most common ways to represent a Graph:
1. Adjacency Matrix
2. Adjacency List
Adjacency Matrix:
 Adjacency Matrix is a 2D array of size V x V where V is the number of
vertices in a graph.
 Let the 2D array be adj [][], a slot adj [i][j] = 1 indicates that there is
an edge from vertex i to vertex j.
 Adjacency matrix for undirected graph is always symmetric.
 Adjacency Matrix is also used to represent weighted graphs.
 If adj [i][j] = w, then there is an edge from vertex i to vertex j with
weight w.

9. Representation Of Graph
Adjacency List:
 An array of lists is used.
 Size of the array is equal to the number of vertices.
 Let the array be array []. An entry array [i] represents the
list of vertices adjacent to the ith vertex.
 This representation can also be used to represent a
weighted graph.
 The weights of edges can be represented as lists of pairs.

10. Representation Of Graph
Example Of Adjacency Matrix Of A Graph:
a 1 2 3
1 0 1 1
2 1 0 1
b c 3 1 1 0
(a) Matrix Representation Of (a)
Example Of Adjacency List Of A Graph:
a
b c
(a)
Head Node Vertex Node
1 2 3 NULL
2 1 3 NULL
3 1 2 NULL

11. Graph Algorithms
Some Basic Graph Algorithms Are:
1.Depth First Search(DFS)
2.Breadth First Search(BFS)
3.Shortest Path Algorithm
4.Dijskstra’s Algorithm

12. Graph Coloring
 Graph Coloring is a method to assign colors to the vertices of a graph
so that no two adjacent vertices have the same color.
Some Graph Coloring problems are :
 Vertex coloring : A way of coloring the vertices of a graph so that no
two adjacent vertices share the same color.
 Edge Coloring : It is the method of assigning a color to each edge so
that no two adjacent edges have the same color.
 Face coloring : It assigns a color to each face or region of a planar
graph so that no two faces that share a common boundary have the
same color.
Chromatic Number:
 Chromatic Number is the minimum number of colors required to
color a graph.

13. THANK YOU
Insert Group
Member Names
Here..