2018年度意思決定会計論第8回講義の資料です。

1. 意思決定会計論⑧
経営意思決定のための会計 Ⅱ

2. • 新製品は現有設備で追加しうる場合と，設備拡張が
必要となる場合がある。
• 注意すべき点
①製造間接費や本社費の配賦額を含む平均原価で
意思決定を下すことは，しばしば誤った結論を導く。
②旧製品の廃棄が問題となるケースでは，P/Lが赤字で
ある場合が多い。
→回避可能原価を関連原価の対象として含む検討を！
新製品の追加または旧製品の廃棄の意思決定

3. • 注意すべき点
③現有設備で新製品を追加する能力を持っていれば，
増分原価だけを考慮する。
→発生が予想される固定費も考慮する。
④ある製品を廃棄して他の製品に代替させるので
あれば，機会原価をも明示的に考慮する。
• 【例題】を解いてみましょう。
新製品の追加または旧製品の廃棄の意思決定

4. 新製品の追加または旧製品の廃棄の意思決定
• 靴の生産を止めても，回避不能固定費180万円は共通固定費（あ
る基準で配賦された）なので，埋没原価である。
• 限界（貢献）利益から個別固定費を除く利益を計算する。
• 解答
与えられた損益計算書は以下のように書き換えられる。
合計 靴 鞄 ベルト
売上高 5,700 3,000 2,400 300
変動費 4,260 2,400 1,680 180
限界利益 1,440 600 720 120
個別固定費 795 450 300 45
利益（個固除く） 645 150 420 75
共通固定費 540
営業利益 105

5. 最適SM，PMの計算
• セールス・ミックス／プロダクト・ミックスの計算
→意思決定問題としては組み合わせの決定の問題
• 2製品，販売上の1つの制約条件下での組み合わせ
→固定費は埋没原価になるので，単位あたりの貢献利益が
大きいものを多く販売すべきである。
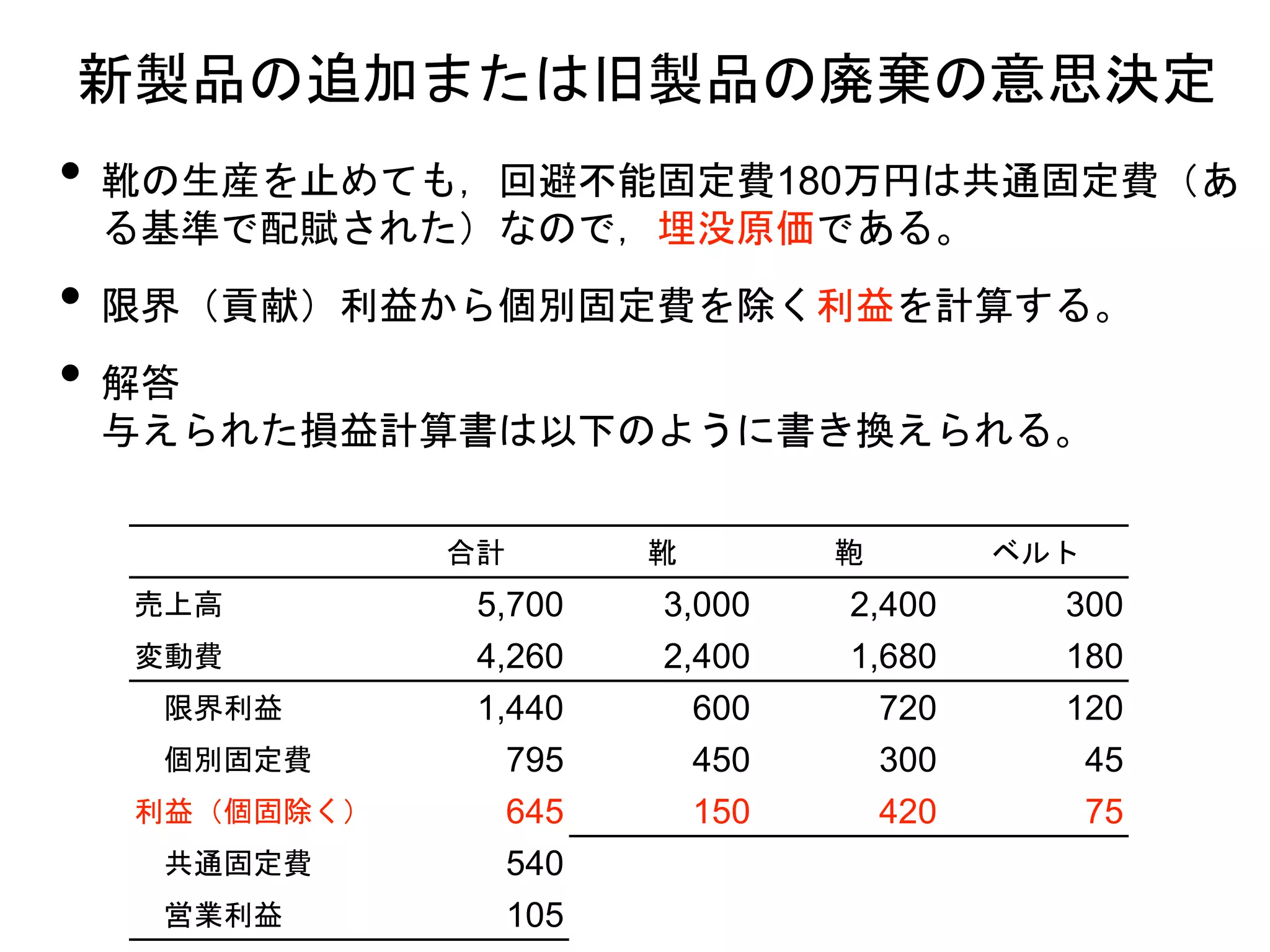
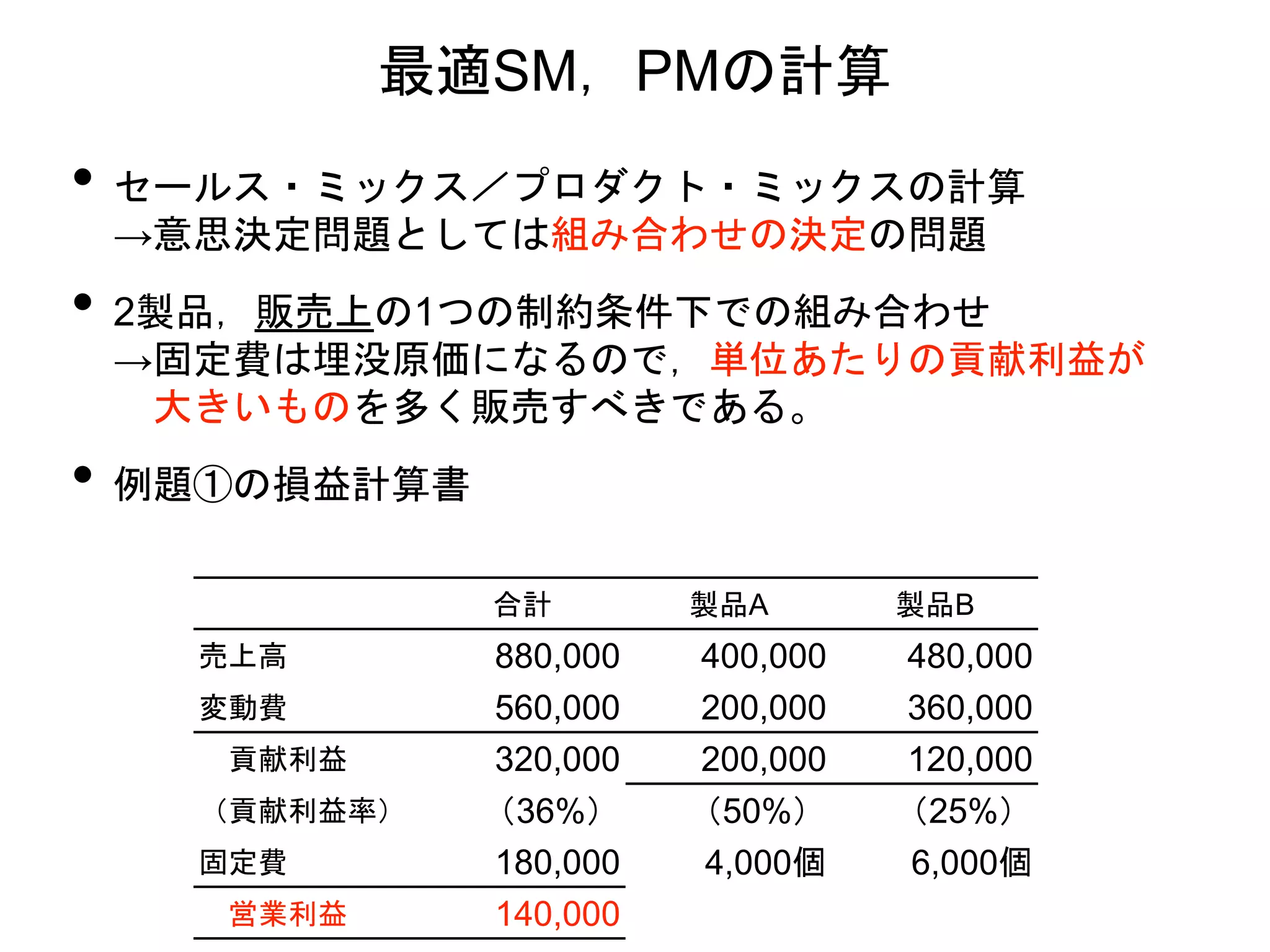
• 例題①の損益計算書
合計 製品A 製品B
売上高 880,000 400,000 480,000
変動費 560,000 200,000 360,000
貢献利益 320,000 200,000 120,000
（貢献利益率） （36%） （50%） （25%）
固定費 180,000 4,000個 6,000個
営業利益 140,000

6. • 2製品，生産上の1つの制約条件下での組み合わせ
→単位あたりの貢献利益が大きいものを多く販売すべきである。
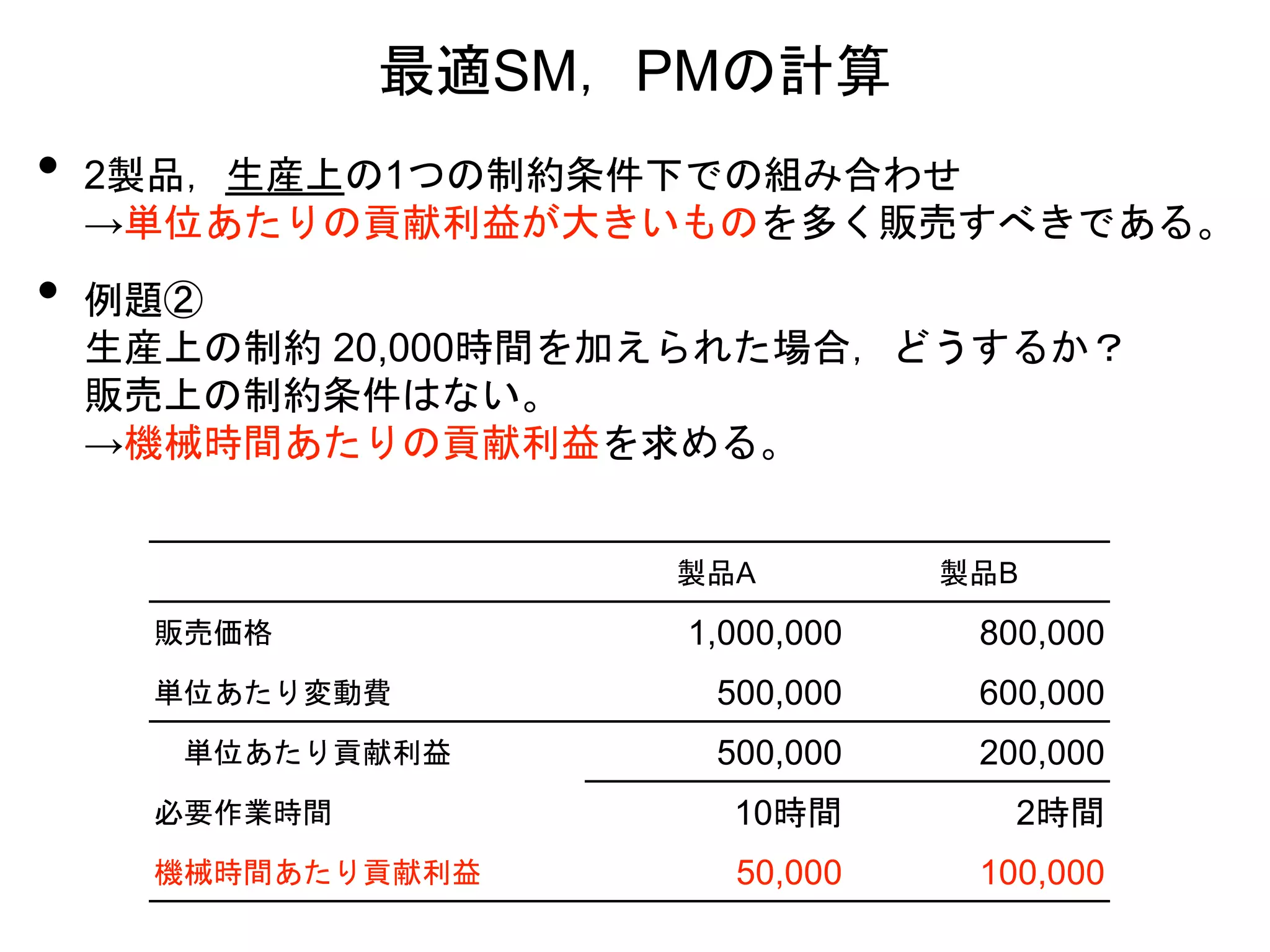
• 例題②
生産上の制約 20,000時間を加えられた場合，どうするか？
販売上の制約条件はない。
→機械時間あたりの貢献利益を求める。
最適SM，PMの計算
製品A 製品B
販売価格 1,000,000 800,000
単位あたり変動費 500,000 600,000
単位あたり貢献利益 500,000 200,000
必要作業時間 10時間 2時間
機械時間あたり貢献利益 50,000 100,000

7. 最適SM，PMの計算
• 製品Bの方が作業時間あたり貢献利益が大きいので，
製品Bを生産すべきである。
製品Bを10,000個生産した場合の利益
800,000万円（売上）−（600,000万円＋180,000万円）
＝20,000万円
製品Aを10,000個生産した場合の利益
200,000万円（売上）−（100,000万円＋180,000万円）
＝△80,000万円

8. 最適SM，PMの計算
• 2製品，販売・生産上の多くの制約条件下での組み合わせ
• 例題③
製品Bについて8,000個が販売限度という制約条件が
付けられた場合，貢献利益を最大にするにはそれぞれ
何個生産すべきか？
• 線形計画法（LP：Linear Programming）
いくつかの制約条件のもとで，ある値を最大（あるいは
最小）にするような変数の値（最適解）を求める。

9. • 与えられた条件を式に置き換える。
製品Aの生産量をA，製品Bの生産量をBとする。
①生産上の制約
10A ＋ 2B ≦ 20,000
②販売上の制約
B製品は8,000個を超えることができない。
B ≦ 8,000
③製品Aと製品Bの限界利益がそれぞれ50万円，20万円
なので，総限界利益をZとすると，
Z = 50A ＋ 20B
最適SM，PMの計算

10. A
B
B=8,000
10,000
8,000
Z=50A＋20B
2,000O
最適SM，PMの計算
←10A＋2B＝20,000
④非負条件
A ≧ 0，B ≧ 0
a
b
c
d
①〜④の条件を
プロットすると
右図のようになる。
a，b，c，dのときの
AとBを求める。

11. • これらを解くと下記の表のようになる。
最適SM，PMの計算
変 数 目的関数の値
A B 50A ＋ 20B
a 0 8,000 50×0＋20×8,000＝160,000
b 400 8,000 50×400＋20×8,000＝180,000
c 2,000 0 50×2,000＋20×0＝100,000
d 0 0 50×0＋20×0＝ 0
よって，Aを400個，Bを8,000個生産すると
限界利益が最大になる。

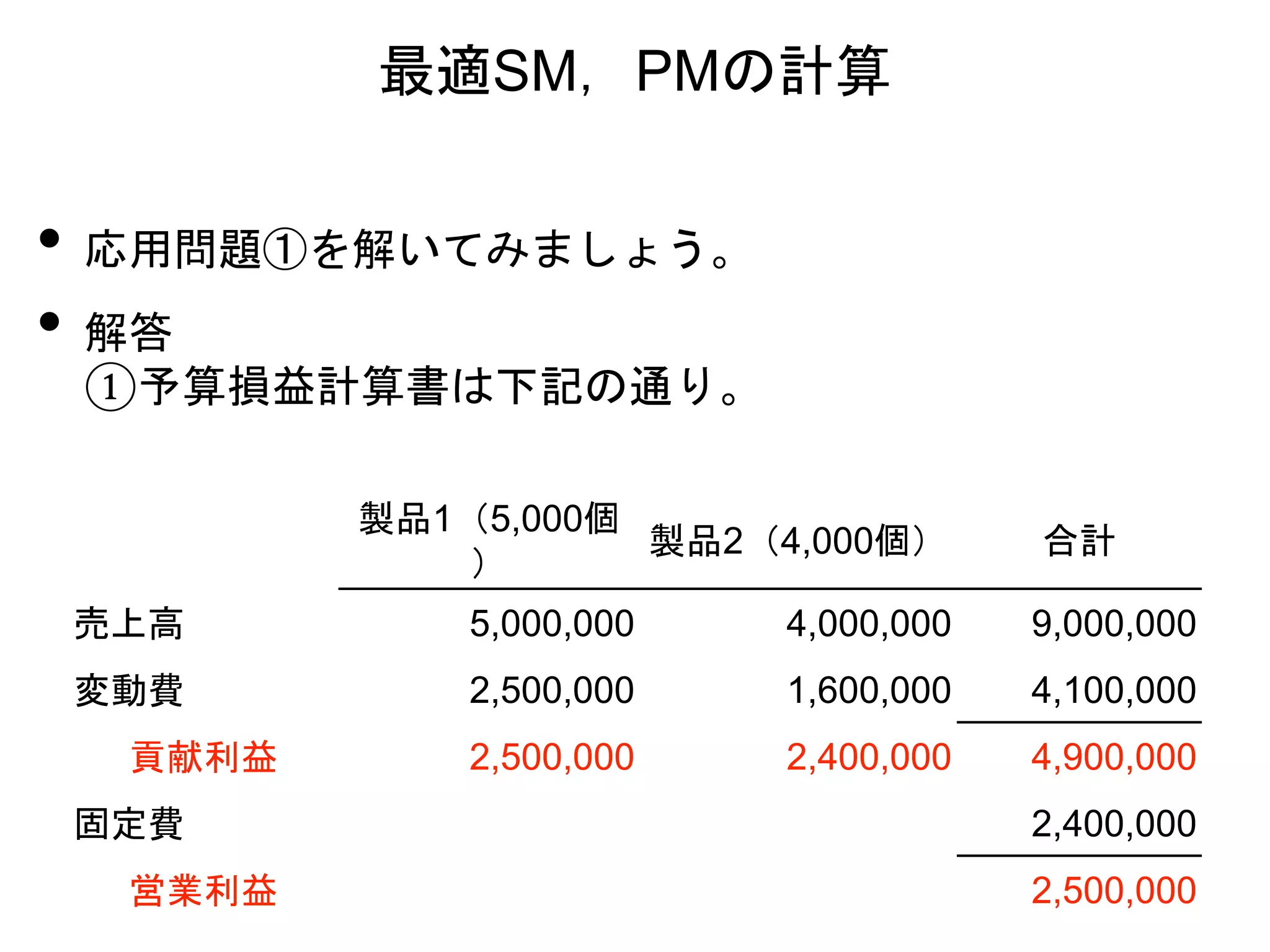
12. • 応用問題①を解いてみましょう。
• 解答
①予算損益計算書は下記の通り。
最適SM，PMの計算
製品1（5,000個
）
製品2（4,000個） 合計
売上高 5,000,000 4,000,000 9,000,000
変動費 2,500,000 1,600,000 4,100,000
貢献利益 2,500,000 2,400,000 4,900,000
固定費 2,400,000
営業利益 2,500,000

13. 最適SM，PMの計算
• 解答
②ここでも収益性の高い製品に優先して制約条件を
振り向ける。制約条件あたりの貢献利益を計算し，
最適セールス・ミックスを判断する。
最適セールス・ミックス
・機械時間あたりの貢献利益
製品1 @500（貢献利益）÷@1時間＝@500円
製品2 @600（貢献利益）÷@2時間＝@300円
・製品1の生産販売量 5,000個
・余剰生産能力 10,000時間−5,000時間＝5,000時間
・製品2の生産販売量 5,000時間÷@2時間＝2,500個

14. 最適SM，PMの計算
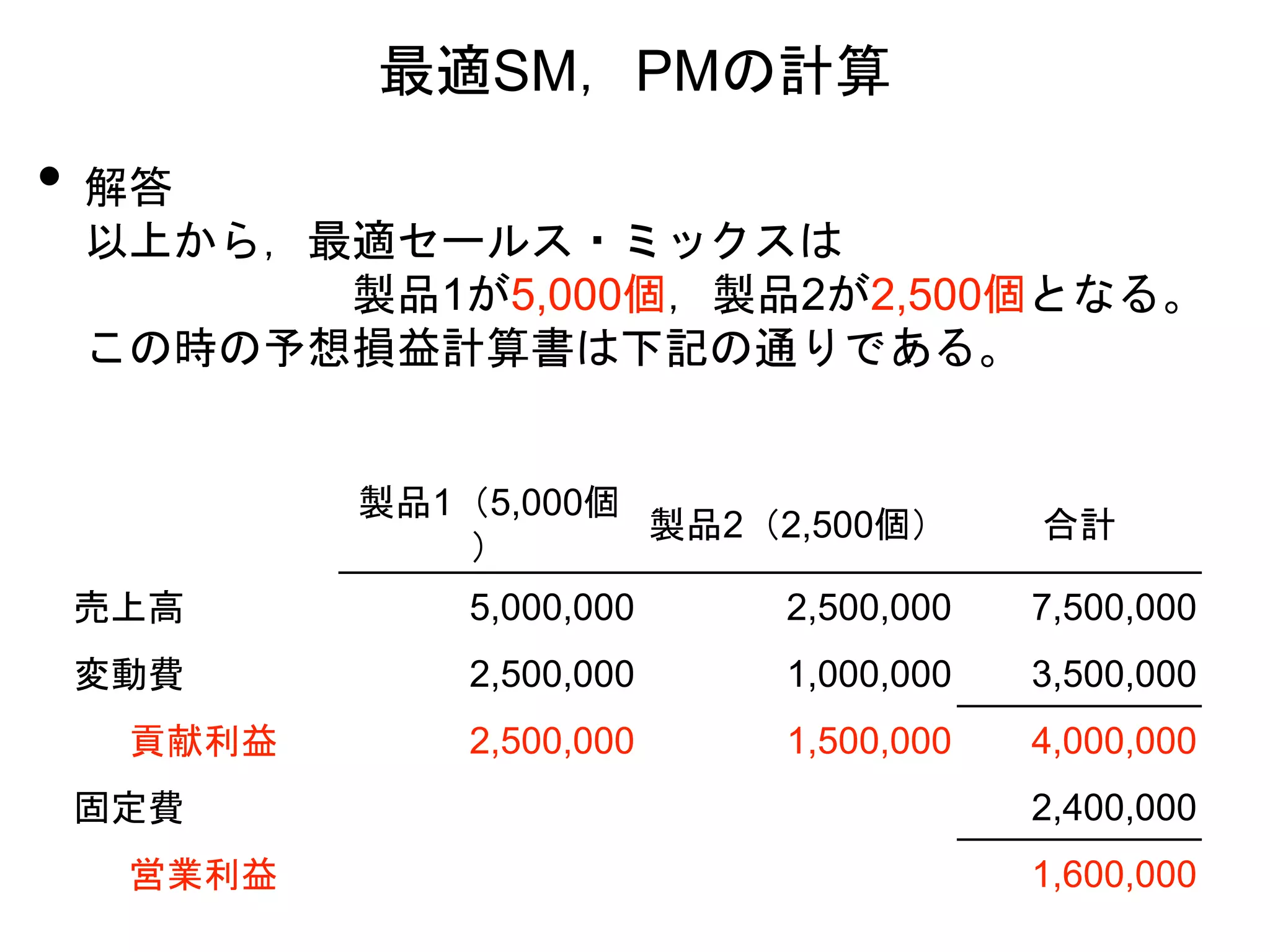
• 解答
以上から，最適セールス・ミックスは
製品1が5,000個，製品2が2,500個となる。
この時の予想損益計算書は下記の通りである。
製品1（5,000個
）
製品2（2,500個） 合計
売上高 5,000,000 2,500,000 7,500,000
変動費 2,500,000 1,000,000 3,500,000
貢献利益 2,500,000 1,500,000 4,000,000
固定費 2,400,000
営業利益 1,600,000

15. • 解答
③与えられたデータをもとに，目的関数と制約条件を
定式化する。
製品1の販売量をA，製品2の販売量をBとし，
貢献利益をZとすると，制約条件は以下の通りとなる。
max Z＝500A＋600B
最適SM，PMの計算
制約条件
機械時間の制約： A ＋ 2B ≦ 10,000
材料の節約 ：3 A ＋ 2B ≦ 18,000
製品1需要量 ： A ≦ 5,000
製品2需要量 ： B ≦ 4,000
非負条件 ： A ， B ≧ 0

16. A
B
a b
c
d
e
9,000
5,000
4,000
10,000↑
5,000
6,000O
最適SM，PMの計算
以上の制約条件からZ（貢献利益）を
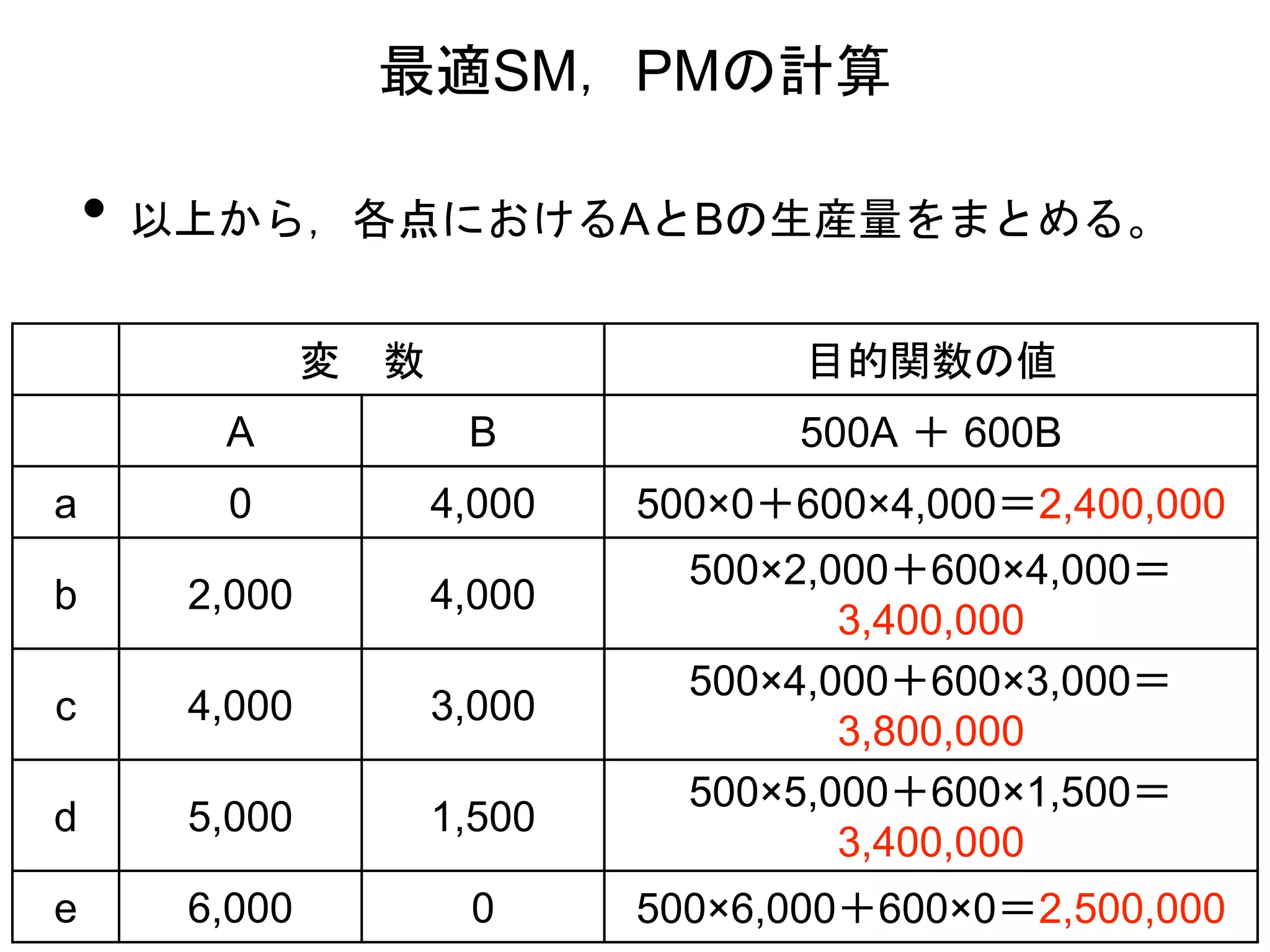
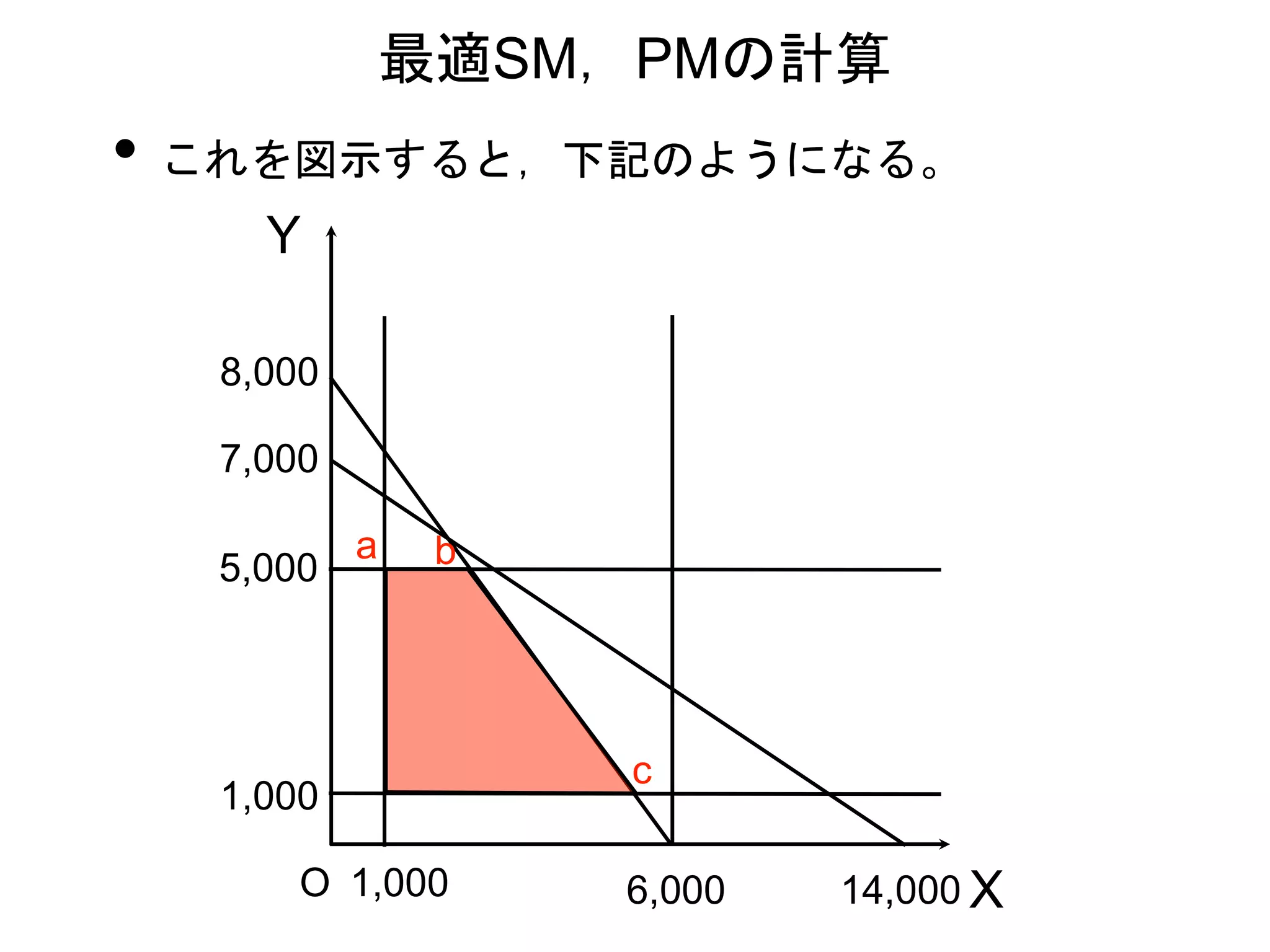
最大化するAとBを求める。

17. • 以上から，各点におけるAとBの生産量をまとめる。
最適SM，PMの計算
変 数 目的関数の値
A B 500A ＋ 600B
a 0 4,000 500×0＋600×4,000＝2,400,000
b 2,000 4,000
500×2,000＋600×4,000＝
3,400,000
c 4,000 3,000
500×4,000＋600×3,000＝
3,800,000
d 5,000 1,500
500×5,000＋600×1,500＝
3,400,000
e 6,000 0 500×6,000＋600×0＝2,500,000

18. • 以上から，貢献利益が最も大きくなるのは c の
組み合わせである。
このときの予想損益計算書は下記の通りである。
最適SM，PMの計算
製品1（4,000個
）
製品2（3,000個） 合計
売上高 4,000,000 3,000,000 7,000,000
変動費 2,000,000 1,200,000 3,200,000
貢献利益 2,000,000 1,800,000 3,800,000
固定費 2,400,000
営業利益 1,400,000

19. • 応用問題②を解きましょう。
• 〔問1〕
各製品の需要限度を満たす作業時間を求める。
最適SM，PMの計算
機械加工部
製品X 4時間×5,000個＝ 20,000時間
製品Y 3時間×4,000個＝ 12,000時間
製品Z 2時間×500個＝ 1,000時間
合計 33,000時間 ≧ 24,000時間

20. • 以上から，需要限度を超えている機械加工部の時間あたり
貢献利益額の大きい順に生産・販売すればよい。
• ただし，各製品の最低生産販売量を確保する必要がある。
製品X 2時間×5,000個＝ 10,000時間
製品Y 4時間×4,000個＝ 16,000時間
製品Z 2時間×500個＝ 1,000時間
合計 27,000時間 ≦ 28,000時間
組立部
最適SM，PMの計算

21. • 機械加工部1時間あたりの貢献利益額
最適SM，PMの計算
製品X （3,200円−2,000円）÷ 4時間＝300円/時間
製品Y （1,800円−1,000円）÷ 3時間 ≒ 267円/時間
製品Z （1,100円−900円）÷2時間＝100円/時間
よって，
時間あたり貢献利益が最も大きい製品Xを5,000個生産し，
時間あたり貢献利益が最も小さい製品Zを50個生産する。
そして，残りの時間で製品Yを生産すると，貢献利益が
最も大きくなる。
以上から，製品Yは
（24,000時間 − 20,000時間 − 2時間×50個）÷3時間
＝1,300個生産する。

22. • 〔問2〕の解答
製品Xの生産販売量をX，製品Yの生産販売量をYとする。
貢献利益をZとすると，Zの目的関数は
maxZ＝max（1,200X＋800Y）となる。
このときの制約条件は下記の通り。
機械加工部の作業時間：4X＋3Y ≦ 24,000
組立部の作業時間 ：2X＋4Y ≦ 28,000
Xの需要量 ：X ≦ 6,000 X ≧ 1,000
Yの需要量 ：Y ≦ 5,000 Y ≧ 1,000
X ≧ 0, Y ≧ 0
最適SM，PMの計算

23. • これを図示すると，下記のようになる。
最適SM，PMの計算
X
Y
a b
c
8,000
5,000
1,000
14,0006,000O
7,000
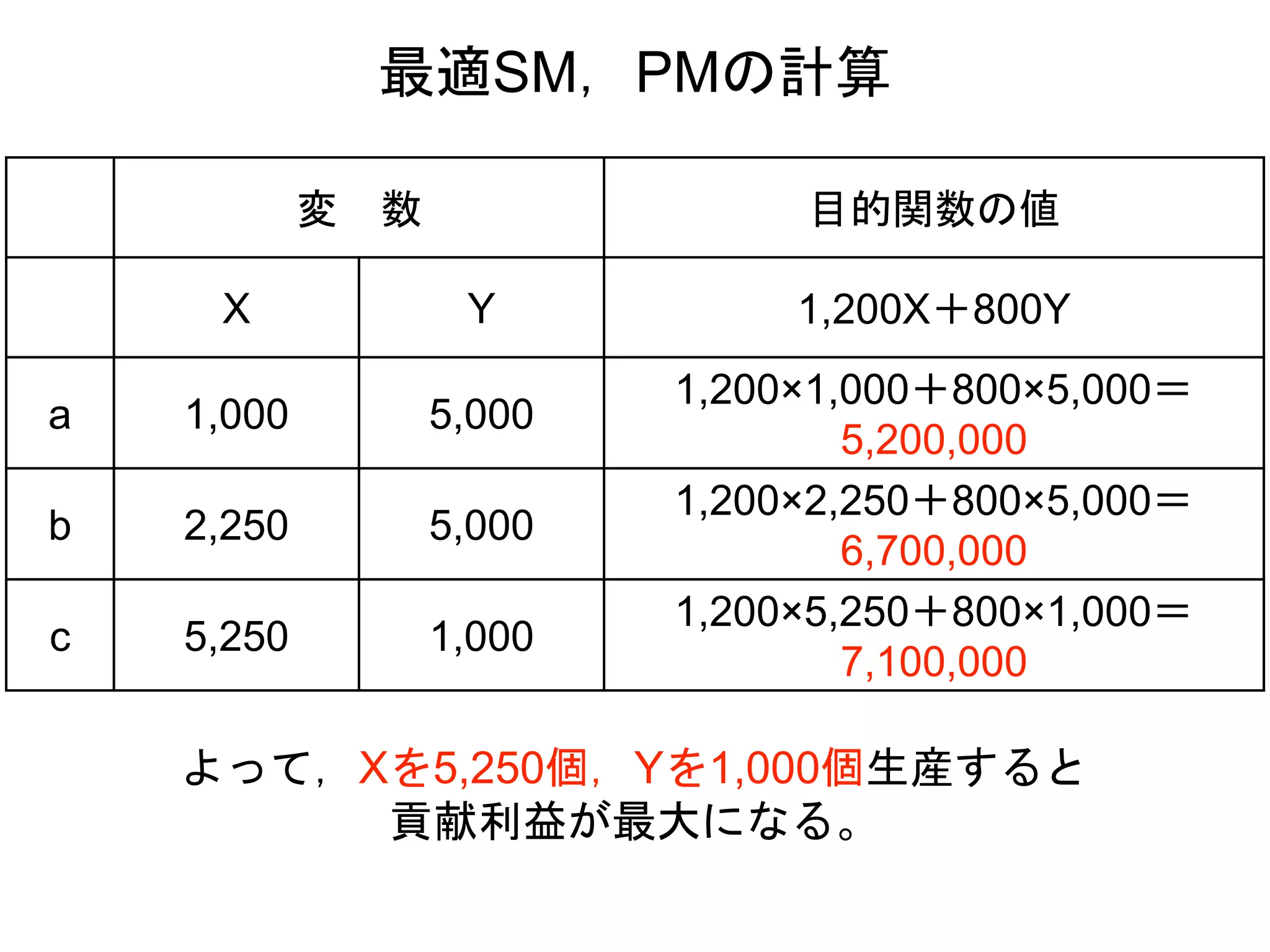
1,000

24. 変 数 目的関数の値
X Y 1,200X＋800Y
a 1,000 5,000
1,200×1,000＋800×5,000＝
5,200,000
b 2,250 5,000
1,200×2,250＋800×5,000＝
6,700,000
c 5,250 1,000
1,200×5,250＋800×1,000＝
7,100,000
最適SM，PMの計算
よって，Xを5,250個，Yを1,000個生産すると
貢献利益が最大になる。

25. • 製品Xの生産販売量をX，製品Yの生産販売量をYとする。
貢献利益をZとすると，Zの目的関数は
maxZ＝max（900X＋800Y）となる。
• 制約条件は下記の通り。
4X＋3Y ≦ 24,000 2X＋4Y ≦ 28,000
X ≦ 6,000 X ≧ 1,000
Y ≦ 7,000 Y ≧ 1,000
X ≧ 0 Y ≧ 0
最適SM，PMの計算

26. • これを図示すると，下記のようになる。
最適SM，PMの計算
X
Y
a
b
c
8,000
1,000
14,0006,000O
7,000
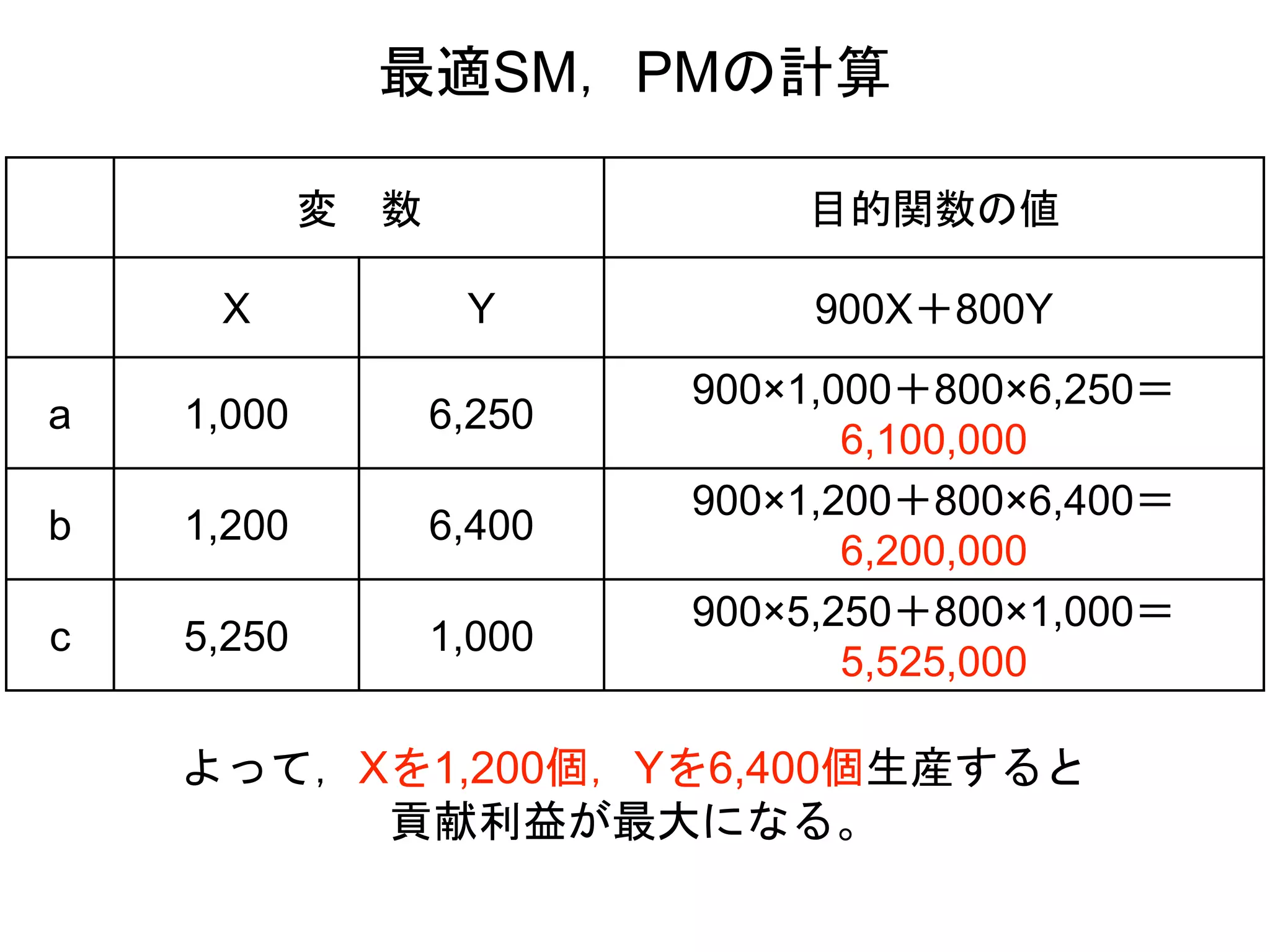
1,000

27. 変 数 目的関数の値
X Y 900X＋800Y
a 1,000 6,250
900×1,000＋800×6,250＝
6,100,000
b 1,200 6,400
900×1,200＋800×6,400＝
6,200,000
c 5,250 1,000
900×5,250＋800×1,000＝
5,525,000
最適SM，PMの計算
よって，Xを1,200個，Yを6,400個生産すると
貢献利益が最大になる。