The document discusses cross entropy loss function which is commonly used in classification problems. It derives the theoretical basis for cross entropy by formulating it as minimizing the cross entropy between the predicted probabilities and true labels. For binary classification problems, cross entropy is shown to be equivalent to maximizing the likelihood of the training data which can be written as minimizing the binary cross entropy. This concept is extended to multiclass classification problems by defining the prediction as a probability distribution over classes and label as a one-hot encoding.

1. Detailed Description
on Cross Entropy Loss Function
ICSL Seminar
김범준
2019. 01. 03

2.  Cross Entropy Loss
- Classification 문제에서 범용적으로 사용
- Prediction과 Label 사이의 Cross Entropy를 계산
- 구체적인 이론적 근거 조사, 직관적 의미 해석
𝐻 𝑃, 𝑄 = −
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔(𝑞𝑖)

3. • Theoretical Derivation
- Binary Classification Problem
- Multiclass Classification Problem
• Intuitive understanding
- Relation to the KL-Divergence

4. • Theoretical Derivation
- Binary Classification Problem
- Multiclass Classification Problem
• Intuitive understanding
- Relation to the KL-Divergence

5. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = 0.1 𝑦1 = 0
Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1

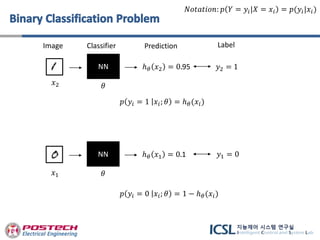
6. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = 0.1 𝑦1 = 0
Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1
[0, 0, 0, 1, 1, 1]
𝑦1, … , 𝑦 𝑚𝑥1, … , 𝑥 𝑚
: Training Dataset
𝜃

7. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = 0.1 𝑦1 = 0
Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1
[0, 0, 0, 1, 1, 1]
𝑦1, … , 𝑦 𝑚𝑥1, … , 𝑥 𝑚
𝐿𝑖𝑘𝑒𝑙𝑖ℎ𝑜𝑜𝑑: 𝐿 𝜃 = 𝑝(𝑦1, … , 𝑦 𝑚|𝑥1, … , 𝑥 𝑚; 𝜃)
: Training Dataset
𝜃
: 에 의해 [0, 0, 0, 1, 1, 1]로 Prediction이 나올법한 정도𝜃
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
입력 image예측 label

8. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = 0.1 𝑦1 = 0
Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1
[0, 0, 0, 1, 1, 1]
𝑦1, … , 𝑦 𝑚𝑥1, … , 𝑥 𝑚
𝐿𝑖𝑘𝑒𝑙𝑖ℎ𝑜𝑜𝑑: 𝐿 𝜃 = 𝑝(𝑦1, … , 𝑦 𝑚|𝑥1, … , 𝑥 𝑚; 𝜃)
𝑀𝑎𝑥𝑖𝑚𝑢𝑚 𝐿𝑖𝑘𝑒𝑙𝑖ℎ𝑜𝑜𝑑: 𝜃 = 𝑎𝑟𝑔𝑚𝑎𝑥(𝐿(𝜃))
: [0, 0, 0, 1, 1, 1]로 Prediction이 가장 나올법한 를 선택한다
𝜃
: 에 의해 [0, 0, 0, 1, 1, 1]로 Prediction이 나올법한 정도𝜃
𝜃
: Training Dataset
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)

9. Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1
𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)

10. Image Classifier Prediction Label
𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = 0.95 𝑦2 = 1
𝑝 𝑦𝑖 = 0 𝑥𝑖; 𝜃 = 1 − ℎ 𝜃(𝑥𝑖)
NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = 0.1 𝑦1 = 0
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)

11. 𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
𝑝 𝑦𝑖 = 0 𝑥𝑖; 𝜃 = 1 − ℎ 𝜃(𝑥𝑖)
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)

12. 𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
𝑝 𝑦𝑖 = 0 𝑥𝑖; 𝜃 = 1 − ℎ 𝜃(𝑥𝑖)
즉, 𝑝 𝑦𝑖 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖
𝑦 𝑖 1 − ℎ 𝜃 𝑥𝑖
1−𝑦 𝑖
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
: 베르누이 분포

13. 𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
𝑝 𝑦𝑖 = 0 𝑥𝑖; 𝜃 = 1 − ℎ 𝜃(𝑥𝑖)
즉, 𝑝 𝑦𝑖 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖
𝑦 𝑖 1 − ℎ 𝜃 𝑥𝑖
1−𝑦 𝑖
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝐿 𝜃 = 𝑝 𝑦1, … , 𝑦 𝑚 𝑥1, … , 𝑥 𝑚; 𝜃
=
𝑖=1
𝑚
𝑝 𝑦𝑖 𝑥𝑖; 𝜃 ∵ 𝑖. 𝑖. 𝑑 𝑎𝑠𝑠𝑢𝑚𝑝𝑡𝑖𝑜𝑛
* i.i.d : independent and identically distributed
: 베르누이 분포

14. 𝑝 𝑦𝑖 = 1 𝑥𝑖; 𝜃 = ℎ 𝜃(𝑥𝑖)
𝑝 𝑦𝑖 = 0 𝑥𝑖; 𝜃 = 1 − ℎ 𝜃(𝑥𝑖)
즉, 𝑝 𝑦𝑖 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖
𝑦 𝑖 1 − ℎ 𝜃 𝑥𝑖
1−𝑦 𝑖
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝐿 𝜃 = 𝑝 𝑦1, … , 𝑦 𝑚 𝑥1, … , 𝑥 𝑚; 𝜃
=
𝑖=1
𝑚
𝑝 𝑦𝑖 𝑥𝑖; 𝜃 ∵ 𝑖. 𝑖. 𝑑 𝑎𝑠𝑠𝑢𝑚𝑝𝑡𝑖𝑜𝑛
=
𝑖=1
𝑚
ℎ 𝜃 𝑥𝑖
𝑦 𝑖 1 − ℎ 𝜃 𝑥𝑖
1−𝑦 𝑖
* i.i.d : independent and identically distributed
: 베르누이 분포

15. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃

16. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃 (∵log는 단조증가 함수)

17. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛( 𝑖=1
𝑚
[−𝑦𝑖 log ℎ 𝜃 𝑥𝑖 − (1 − 𝑦𝑖) log(1 − ℎ 𝜃 𝑥𝑖 )]) (∵ 𝑙𝑜𝑔 성질)
𝐿 𝜃 =
𝑖=1
𝑚
ℎ 𝜃 𝑥𝑖
𝑦 𝑖 1 − ℎ 𝜃 𝑥𝑖
1−𝑦 𝑖

18. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛( 𝑖=1
𝑚
[−𝑦𝑖 log ℎ 𝜃 𝑥𝑖 − (1 − 𝑦𝑖) log(1 − ℎ 𝜃 𝑥𝑖 )])
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
𝑤ℎ𝑒𝑟𝑒 𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖 = −𝑦𝑖 log ℎ 𝜃 𝑥𝑖 − 1 − 𝑦𝑖 log 1 − ℎ 𝜃 𝑥𝑖
: 𝐵𝑖𝑛𝑎𝑟𝑦 𝐶𝑟𝑜𝑠𝑠 𝐸𝑛𝑡𝑟𝑜𝑝𝑦

19. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛( 𝑖=1
𝑚
[−𝑦𝑖 log ℎ 𝜃 𝑥𝑖 − (1 − 𝑦𝑖) log(1 − ℎ 𝜃 𝑥𝑖 )])
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
𝑤ℎ𝑒𝑟𝑒 𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖 = −𝑦𝑖 log ℎ 𝜃 𝑥𝑖 − 1 − 𝑦𝑖 log 1 − ℎ 𝜃 𝑥𝑖
: 𝐵𝑖𝑛𝑎𝑟𝑦 𝐶𝑟𝑜𝑠𝑠 𝐸𝑛𝑡𝑟𝑜𝑝𝑦
ℎ 𝜃 𝑥𝑖 , 𝑦𝑖 ∈ 0, 1 인 확률값
Maximize Likelihood Minimize Binary Cross Entropy
Binary Classification Problem

20. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = [𝟎. 𝟗, 0.05, 0.05] 𝑦1 = [1, 0, 0]
Image Classifier Prediction Label
NN
𝑥2 𝜃
ℎ 𝜃 𝑥2 = [0.03, 𝟎. 𝟗𝟓, 0.02] 𝑦2 = [0, 1, 0]
NN
𝑥3 𝜃
ℎ 𝜃 𝑥3 = [0.01, 0.01, 𝟎. 𝟗𝟖] 𝑦3 = [0, 0, 1]

21. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = [𝟎. 𝟗, 0.05, 0.05] 𝑦1 = [1, 0, 0]
Image Classifier Prediction Label
𝑝 𝑦𝑖 = [1, 0, 0] 𝑥𝑖; 𝜃
= 𝑝 𝑦𝑖(0) = 1 𝑥𝑖; 𝜃) (𝐴𝑠𝑠𝑢𝑚𝑒 𝑂𝑛𝑒ℎ𝑜𝑡 𝑒𝑛𝑐𝑜𝑑𝑖𝑛𝑔)

22. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = [𝟎. 𝟗, 0.05, 0.05] 𝑦1 = [1, 0, 0]
Image Classifier Prediction Label
𝑝 𝑦𝑖 = [1, 0, 0] 𝑥𝑖; 𝜃
= 𝑝 𝑦𝑖(0) = 1 𝑥𝑖; 𝜃)
= ℎ 𝜃 𝑥𝑖 (0)

23. NN
𝑥1 𝜃
ℎ 𝜃 𝑥1 = [𝟎. 𝟗, 0.05, 0.05] 𝑦1 = [1, 0, 0]
Image Classifier Prediction Label
𝑝 𝑦𝑖 = [1, 0, 0] 𝑥𝑖; 𝜃
= 𝑝 𝑦𝑖(0) = 1 𝑥𝑖; 𝜃)
= ℎ 𝜃 𝑥𝑖 (0)
같은 방법으로,
𝑝 𝑦𝑖 = [0, 1, 0] 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 1
𝑝 𝑦𝑖 = [0, 0, 1] 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 (2)

24. 𝑝 𝑦𝑖 = [1, 0, 0] 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 (0)
𝑝 𝑦𝑖 = [0, 1, 0] 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 1
𝑝 𝑦𝑖 = [0, 0, 1] 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 (2)
즉, 𝑝 𝑦𝑖 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 0 𝑦 𝑖(0)
ℎ 𝜃 𝑥𝑖 1 𝑦 𝑖(1)
ℎ 𝜃 𝑥𝑖 2 𝑦 𝑖(2)
𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)

25. 𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃

26. 𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
[−𝑦𝑖 0 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(0) − 𝑦𝑖 1 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(1) − 𝑦𝑖 2 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(2)]
𝑝 𝑦𝑖 𝑥𝑖; 𝜃 = ℎ 𝜃 𝑥𝑖 0 𝑦 𝑖(0)
ℎ 𝜃 𝑥𝑖 1 𝑦 𝑖(1)
ℎ 𝜃 𝑥𝑖 2 𝑦 𝑖(2)

27. 𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
[−𝑦𝑖 0 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(0) − 𝑦𝑖 1 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(1) − 𝑦𝑖 2 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(2)]
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
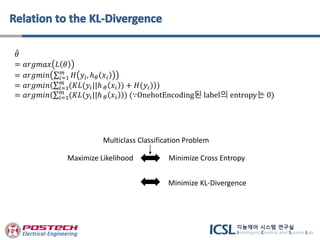
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
𝑤ℎ𝑒𝑟𝑒 𝐻 𝑃, 𝑄 = −
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔(𝑞𝑖)
: 𝐶𝑟𝑜𝑠𝑠 𝐸𝑛𝑡𝑟𝑜𝑝𝑦

28. 𝑁𝑜𝑡𝑎𝑡𝑖𝑜𝑛: 𝑝 𝑌 = 𝑦𝑖|𝑋 = 𝑥𝑖 = 𝑝(𝑦𝑖|𝑥𝑖)
𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛(− 𝑙𝑜𝑔 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
[−𝑦𝑖 0 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(0) − 𝑦𝑖 1 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(1) − 𝑦𝑖 2 𝑙𝑜𝑔ℎ 𝜃(𝑥𝑖)(2)]
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
ℎ 𝜃 𝑥𝑖 , 𝑦𝑖는 Probability Distribution
Maximize Likelihood Minimize Cross Entropy
Multiclass Classification Problem
𝑤ℎ𝑒𝑟𝑒 𝐻 𝑃, 𝑄 = −
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔(𝑞𝑖)
: 𝐶𝑟𝑜𝑠𝑠 𝐸𝑛𝑡𝑟𝑜𝑝𝑦

29. • Theoretical Derivation
- Binary Classification Problem
- Multiclass Classification Problem
• Intuitive understanding
- Relation to the KL-Divergence

30. 𝐻 𝑃, 𝑄
=
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔
1
𝑞𝑖
* KL-Divergence : Kullback–Leibler divergence

31. 𝐻 𝑃, 𝑄
=
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔
1
𝑞𝑖
=
𝑖=1
𝑐
(𝑝𝑖 𝑙𝑜𝑔
𝑝𝑖
𝑞𝑖
+ 𝑝𝑖 𝑙𝑜𝑔
1
𝑝𝑖
)

32. 𝐻 𝑃, 𝑄
=
𝑖=1
𝑐
𝑝𝑖 𝑙𝑜𝑔
1
𝑞𝑖
=
𝑖=1
𝑐
(𝑝𝑖 𝑙𝑜𝑔
𝑝𝑖
𝑞𝑖
+ 𝑝𝑖 𝑙𝑜𝑔
1
𝑝𝑖
)
= 𝐾𝐿(𝑃| 𝑄 + 𝐻(𝑃)
P 자체가 갖는 entropy
KL-Divergence
Cross-entropy

33. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
Maximize Likelihood Minimize Cross Entropy
Multiclass Classification Problem

34. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
(𝐾𝐿(𝑦𝑖||ℎ 𝜃 𝑥𝑖 ) + 𝐻(𝑦𝑖) ) (∵ 𝐻 𝑃, 𝑄 = 𝐾𝐿(𝑃| 𝑄 + 𝐻 𝑃 )

35. 𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
(𝐾𝐿(𝑦𝑖||ℎ 𝜃 𝑥𝑖 ) + 𝐻(𝑦𝑖) )
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
(𝐾𝐿(𝑦𝑖||ℎ 𝜃 𝑥𝑖 ) (∵OnehotEncoding된 label의 entropy는 0)

36. Maximize Likelihood Minimize Cross Entropy
Multiclass Classification Problem
Minimize KL-Divergence
𝜃
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝐿 𝜃
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
𝐻 𝑦𝑖, ℎ 𝜃 𝑥𝑖
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
(𝐾𝐿(𝑦𝑖||ℎ 𝜃 𝑥𝑖 ) + 𝐻(𝑦𝑖) )
= 𝑎𝑟𝑔𝑚𝑖𝑛 𝑖=1
𝑚
(𝐾𝐿(𝑦𝑖||ℎ 𝜃 𝑥𝑖 ) (∵OnehotEncoding된 label의 entropy는 0)

37.  정보 이론의 관점에서는 KL-divergence를 직관적으로 “놀라움의 정도”로 이해 가능
 (예) 준결승 진출팀 : LG 트윈스, 한화 이글스, NC 다이노스, 삼성 라이온즈
- 예측 모델 1) :
- 예측 모델 2) :
- 경기 결과 :
- 예측 모델 2)에서 더 큰 놀라움을 확인
- 놀라움의 정도를 최소화  Q가 P로 근사됨  두 확률 분포가 닮음  정확한 예측
𝑦 = 𝑃 = [1, 0, 0, 0]
𝑦 = 𝑄 = [𝟎. 𝟗, 0.03, 0.03, 0.04]
𝑦 = 𝑄 = [0.3, 𝟎. 𝟔 0.05, 0.05]
𝐾𝐿(𝑃| 𝑄 =
𝑖=1
𝑐
(𝑝𝑖 𝑙𝑜𝑔
𝑝𝑖
𝑞𝑖
)

38. Maximize Likelihood Minimize Cross Entropy
Multiclass Classification Problem
Minimize KL-Divergence
Minimize Surprisal
Approximate prediction to label
Better classification performance in general