Download as PDF, PPTX
推定と標本抽出
- 1.
- 2.
- 3. 発表の流れ 1. 統計的推定について 1. 「推定」とは 2.「推定のよさ」とは 2. Rを使ったシミュレーションよる標本抽出法の比較 1. 単純無作為抽出法 2. 多段抽出法 3. 層化抽出法
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13. 標本抽出法を比べる２ ① 推定値のよさは平均と分散から評価できる ② 「標本の平均」の平均は 単純無作為抽出＝多段抽出＝層化抽出＝母集団の平均 ③「標本の平均」の分散は 多段抽出＞単純無作為抽出＞層化抽出 ①、②、③から、推定のよさは 多段抽出＜単純無作為抽出＜層化抽出
- 14.
- 15. 層化抽出が有効である条件 ① 母集団における各層（グループ）の割合がわかっている 例：ある学年における各クラスの割合 ② 標本抽出枠（名簿）に層のデータが含まれる 例：学年名簿に所属クラスが記されている ③層ごとに母数が異なる（⇒理由は後述） 例：クラスごとにテストの平均得点が異なる ①、または②が満たされないとき次善の策として単純無作為抽出がとられる ③が満たされないとき、層化抽出の精度は単純無作為抽出と同じ
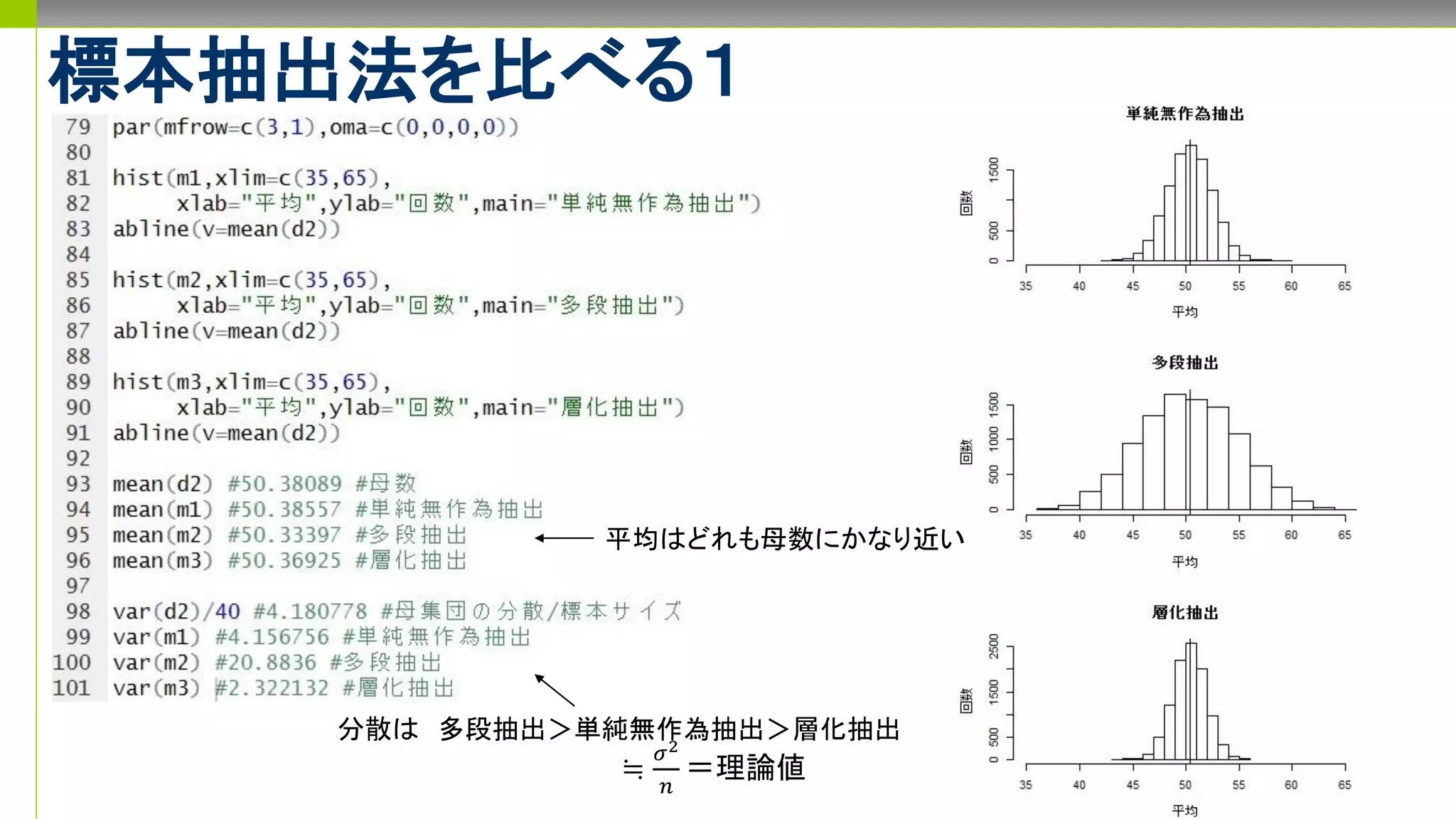
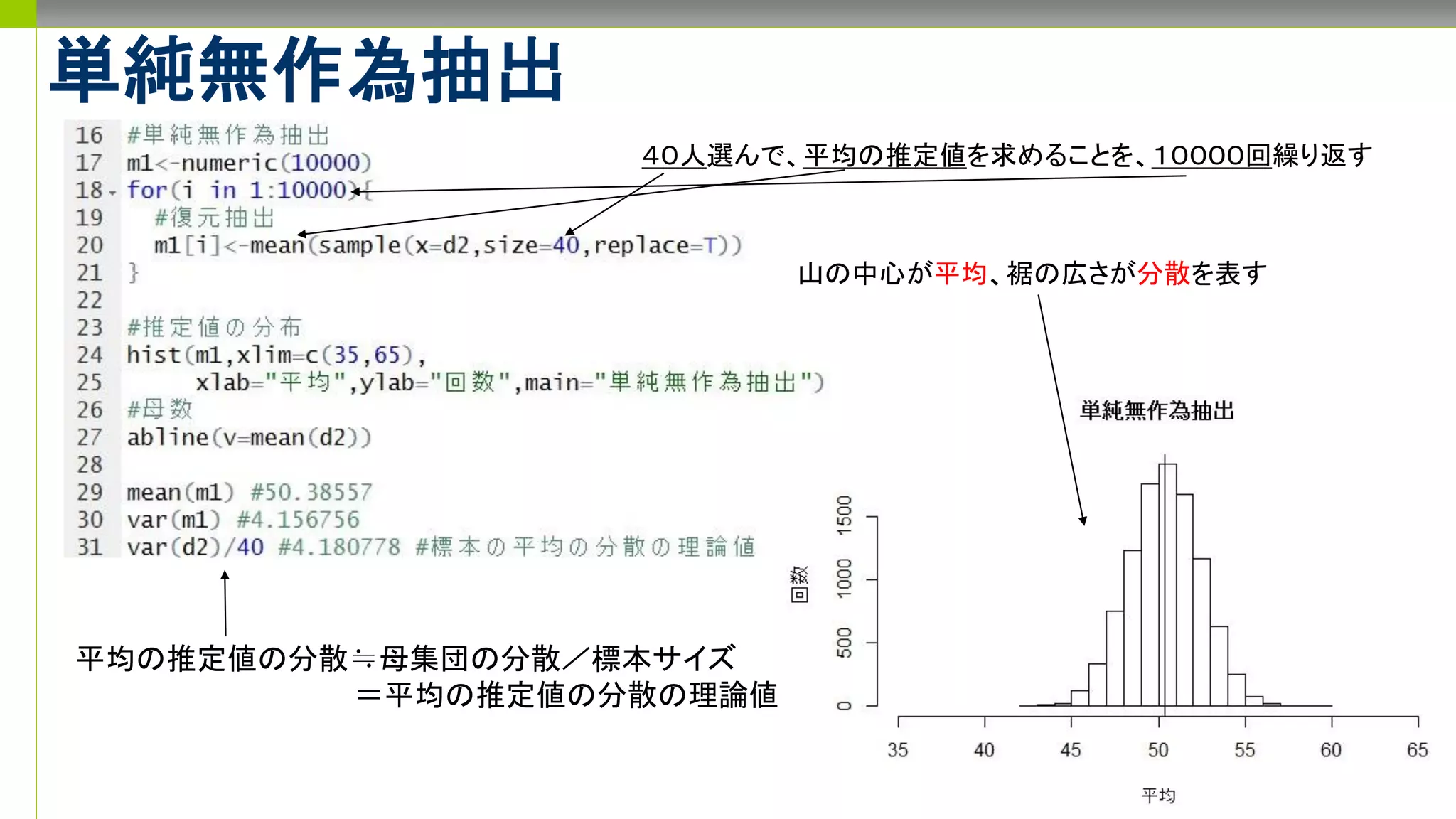
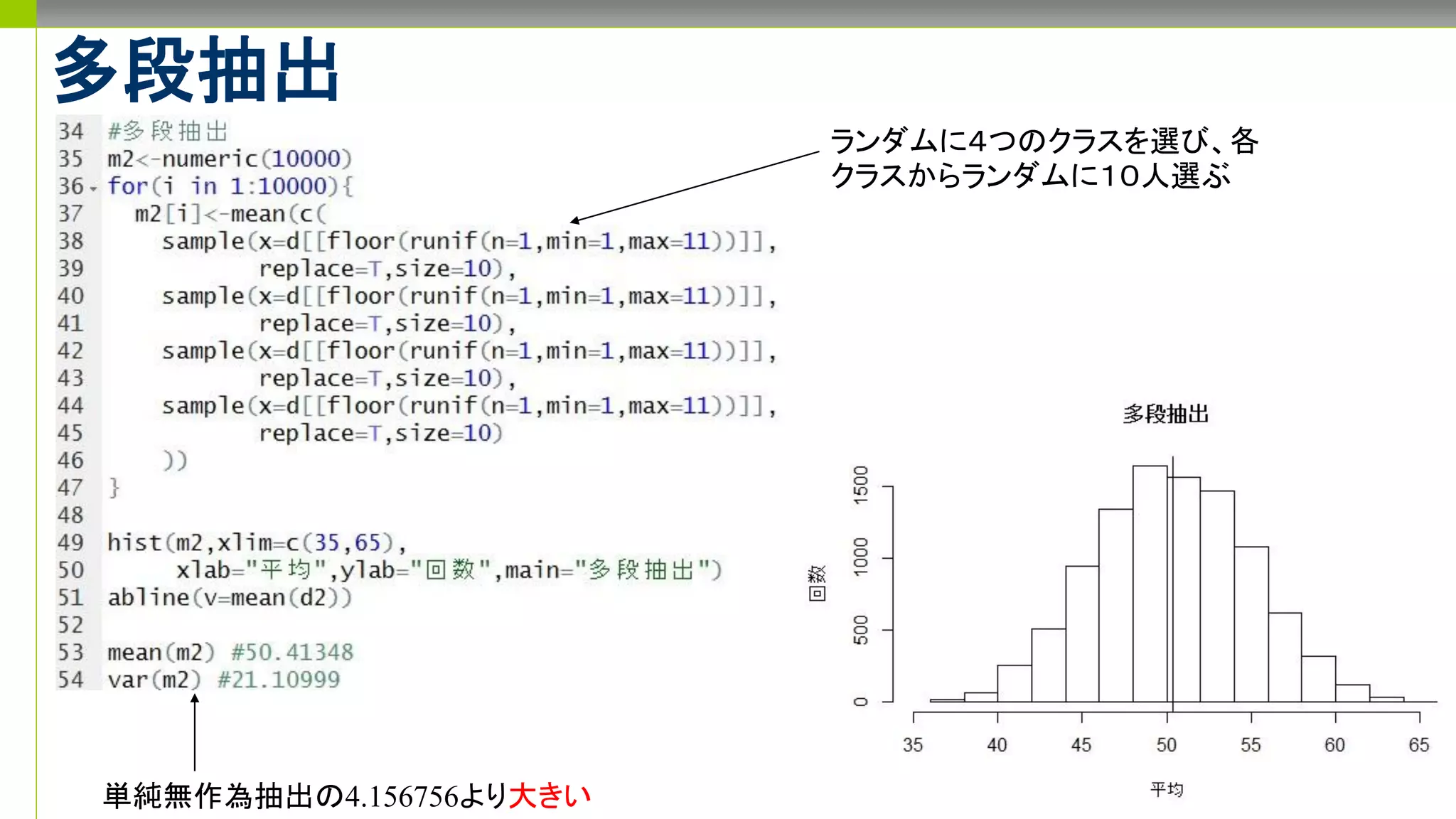
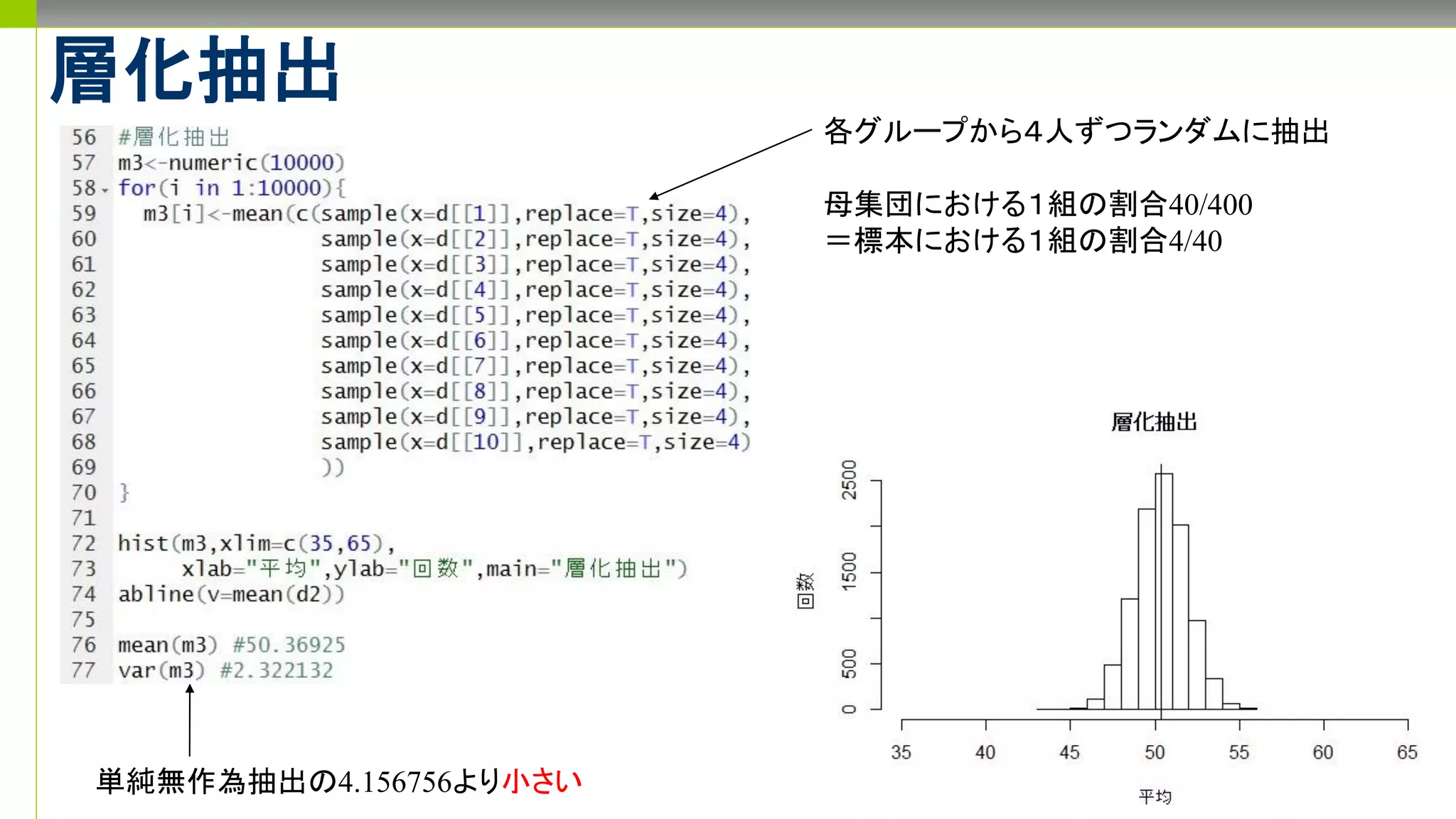
- 16. 標本抽出法を比べる３ 標本抽出法 推定値の平均 推定値の分散調査コスト 単純無作為抽出 ◯ 母数と同じ △ 普通 計算しやすい △ 調査対象が散らばる 多段抽出 △ （割当てをうまくやれば） 母数と同じ × 層ごとに母数が異なる ほど大きくなりやすい 計算しづらい ◯ グループごとに調査対 象がまとまる 層化抽出 △ （割当てをうまくやれば） 母数と同じ ◯ 層ごとに母数が異なる ほど小さくなりやすい 計算しづらい × 調査対象が散らばる 層の割り当てにコストが かかる
- 17. 層化抽出の優位性２ 単純無作為抽出の場合 ①標本平均の分散＝母分散／標本サイズ ②母分散＝母集団の偏差平方和／母集団のサイズ ③母集団の偏差平方和＝郡内平方和＋群間平方和 ＃平方和分解 ①に②、③を代入 ④標本平均の分散＝（郡内平方和＋群間平方和）／母集団のサイズ／標本サイズ 層化抽出の場合 ⑤標本平均の分散＝∑（i組の分散×i組のサイズ）／母集団のサイズ／標本サイズ ＃①と加重平均 ⑥郡内平方和＝∑（i組の分散×i組のサイズ) ⑤に⑥を代入 ⑦標本平均の分散＝群内平方和／母集団のサイズ／標本サイズ 単純無作為抽出と層化抽出の差 標本平均の分散の差＝④ー⑦＝群間平方和／母集団のサイズ／標本サイズ 層ごとに平均（母数）が異なるほど、層化抽出の効果が大きい
- 18.
- 19.