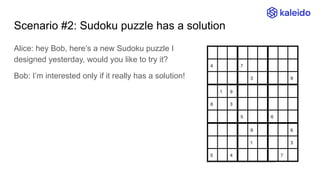
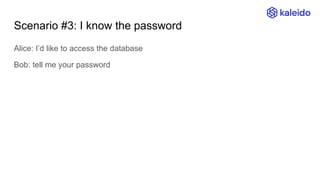
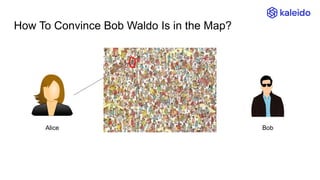
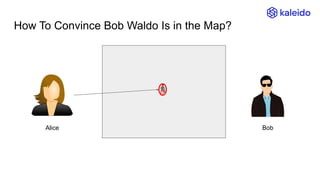
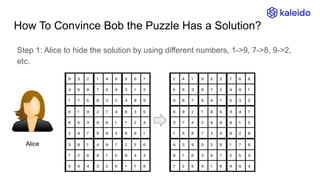
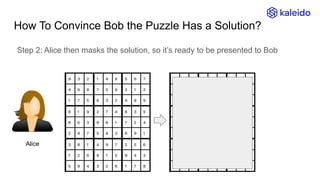
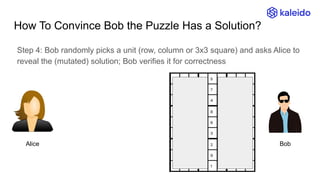
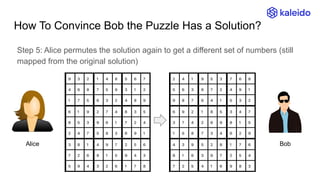
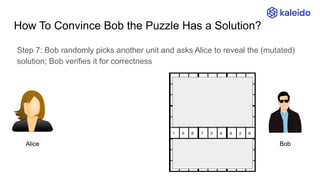
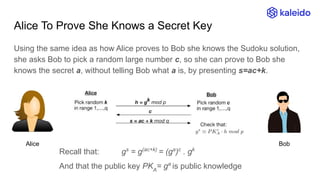
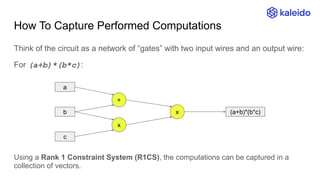
The document explains the concept of Zero-Knowledge Proofs (ZKPs) through examples, outlining how one party (Alice) can convince another party (Bob) of specific information without revealing it. It covers various scenarios, practical applications, and the transition from interactive to non-interactive protocols, highlighting the functionality of SNARK (Succinct Non-interactive Argument of Knowledge) as a popular ZKP scheme. Additionally, it discusses the significance of ZKPs in digital signatures, blockchain transactions, and identity verification.

1. Zero Knowledge Proof:
What It Is and How It Works
Jim Zhang, Co-Founder, Head of Protocol
Kaleido

2. Agenda
Using Examples To Think About the Concept of “Zero Knowledge”
zkSNARK Construction
Application of ZKPs
Further Reading and Hands-on Tutorials

3. Who Is Jim?
Co-founder of Kaleido, Head of Protocol
Committer of Hyperledger FireFly FabConnect
Serves on the Hyperledger Technical Steering Committee
Used to be the lead architect of IBM Blockchain Platform and committer of
Hyperledger Fabric

4. Scenario #1: Where’s Waldo
Alice runs a booth in the state fair, showing a
large picture with thousands of people. If
someone finds it in under 10 seconds, there’s a
prize.
How does she convince Bob, who couldn’t
manage to find Waldo in time, that Waldo is really
in the picture?
Obviously she doesn’t want to simply point Bob to
Waldo in the picture, such that Bob can tell future
players and ruin her game.

5. Scenario #2: Sudoku puzzle has a solution
Alice: hey Bob, here’s a new Sudoku puzzle I
designed yesterday, would you like to try it?
Bob: I’m interested only if it really has a solution!

6. Scenario #3: I know the password
Alice: I’d like to access the database
Bob: tell me your password

7. “Zero Knowledge”
Alice wants to convince Bob of something
● Waldo is in the picture
● The Sudoku puzzle has a solution
● Alice is not an imposter
Bob should not learn “too much”
● Waldo’s location
● The Sudoku solution
● Alice’s password
Mike Rosulek (UIUC)

8. How To Convince Bob Waldo Is in the Map?
Alice Bob

9. How To Convince Bob Waldo Is in the Map?
Alice Bob

10. How To Convince Bob the Puzzle Has a Solution?
Step 1: Alice to hide the solution by using different numbers, 1->9, 7->8, 9->2,
etc.
Alice

11. How To Convince Bob the Puzzle Has a Solution?
Step 2: Alice then masks the solution, so it’s ready to be presented to Bob
Alice

12. How To Convince Bob the Puzzle Has a Solution?
Step 3: the masked solution is presented to Bob
Alice Bob

13. How To Convince Bob the Puzzle Has a Solution?
Step 4: Bob randomly picks a unit (row, column or 3x3 square) and asks Alice to
reveal the (mutated) solution; Bob verifies it for correctness
Alice Bob

14. How To Convince Bob the Puzzle Has a Solution?
Step 5: Alice permutes the solution again to get a different set of numbers (still
mapped from the original solution)
Alice Bob

15. How To Convince Bob the Puzzle Has a Solution?
Step 6: the new masked solution is presented to Bob
Alice Bob

16. How To Convince Bob the Puzzle Has a Solution?
Step 7: Bob randomly picks another unit and asks Alice to reveal the (mutated)
solution; Bob verifies it for correctness
Alice Bob

17. How To Convince Bob the Presented Solution Is For the
Right Puzzle?
Step 8: for any round, Bob could also ask for the original positions of the puzzle to be
disclosed. Seeing the scrambled numbers, Bob can be convinced that it’s properly
mapped from the original public positions
Alice Bob
5
4
8
9
2
2
3 4
7 6
2 6
9 3
7 5 8

18. How To Convince Bob the Puzzle Has a Solution?
Repeat the procedure (mutate -> mask -> pick unit) n times, if Alice gets it right
every time, Bob knows that the chance she achieved this by cheating without a
valid solution, is at most (27/28)n
. For n=200, the chance is ~ 0.05%
Alice Bob
The above protocol for Zero Knowledge Proof is
a probabilistic proof
…

19. Per the Computational Complexity Theory, the Sudoku puzzle is known to be in
the complexity class NP-Complete.
What this means is that, the protocol Alice designed above, can be used to solve
ANY problem in the NP class, by translating it into the Sudoku puzzle.
In practice, turning every problem into a Sudoku puzzle is too inefficient. So we
need to design the proof protocol around a different kind of puzzle in the
NP-Complete class.
Enter the world of large number factorization and logarithm maths.
Can The Previous Protocols Be Generalized?

20. Alice To Prove She Knows a Secret Key
A secret key in the world of cryptography is a large random number, a.
The corresponding public key is PK = ga
We know from math that:
- g(ac)
= (ga
)c
= PKc
- gm
. gk
= g(m+k)

21. Alice To Prove She Knows a Secret Key
Alice Bob
Using the same idea as how Alice proves to Bob she knows the Sudoku solution,
she asks Bob to pick a random large number c, so she can prove to Bob she
knows the secret a, without telling Bob what a is, by presenting s=ac+k.
Recall that: gs
= g(ac+k)
= (ga
)c
. gk
And that the public key PKA
= ga
is public knowledge

22. From Interactive to Non-Interactive
The above protocol requires both parties, Alice (prover), and Bob (verifier) to be
online and are able to interact with each other in real time.
In addition, Alice and Bob are not able to convince a 3rd party, Charlie, that the
proof based on the interactions b/w Alice and Bob have been conducted honestly.
That’s because Alice and Bob could have colluded, such that Bob tells Alice all the
“random” picks ahead of time, so Alice could come up with the right answer.
For a robust protocol, we need to make it work in non-interactive mode.

23. Converting to Non-Interactive
Bob’s role in the interactions is to pick the random challenge value c. What if we
replace Bob’s random number generator with a verifiable random number
generator function that Alice can run to produce c?
Alice could produce c as c = H(gk
|| M) where H() is a hash function, and M
is an (optional) and arbitrary message string

24. From Interactive to Non-Interactive
With the challenges generated by Alice herself, using a “random number
generator” (really called a random oracle) , she can present a proof directly to
Bob.
Alice Bob
proof

25. Time To Get Technical
We now look at one of the most popular zero knowledge proof schemes: SNARK
(succinct non-interactive argument of knowledge).
Given a function f(x), and public output y, using zkSNARK, one can generate a
proof to demonstrate the knowledge of a solution s, without revealing the value of
s.
Given: f(x) = y
Produce s, such as that f(s) = y
SNARK consumes the “code” of the function f(x) and public input y as input, and
produces the zk proof as the output.

26. Converting Functions into SNARK Circuits
Suppose our target function f(x) is a polynomial equation,
f(x) = x3
- x + 7 mod 13
Alice wants to generate a proof that she knows a solution to f(x) ≡ 12.
She first writes the function in Circom language (circuit compiler):
template FakeHash() {
signal private input x;
signal x_squared;
signal x_cubed;
signal output out;
x_squared <== x * x;
x_cubed <== x_squared * x;
out <== x_cubed - x + 7;
}
component main = FakeHash();
- Only 3 operations: +, -, *
- Only operated on elements in prime fields

27. How To Capture Performed Computations
Think of the circuit as a network of “gates” with two input wires and an output wire:
For (a+b)*(b*c):
a
b
c
+
x
x (a+b)*(b*c)
Using a Rank 1 Constraint System (R1CS), the computations can be captured in a
collection of vectors.

28. “Compress” The Verifier’s Task
Now that all the computations performed by the prover have been captured, the
verifier just need to check each of the steps in the computation.
But is it possible to make the verification faster? It’d be ideal to have a protocol
that’s easier to verify than to compute.
We can use another transformation with Quadratic Arithmetic Programs to turn
the result of the R1CS vectors into polynomial expressions.
P(x) = c0
+ c1
x1
+ c2
x2
+ … + cd
xd

29. Why Polynomials?
Two interesting properties about polynomials are useful:
- One expression can embed infinite amount of information
- The coefficients of a polynomial can represent arbitrary information
- Comparing the knowledge of the set of coefficients of a polynomial is easy
- Just plug in a few x values, if Alice is able to return the expected result, then she must know
the set of coefficients

30. Almost There
With the transformations so far, the problem becomes this:
- Alice needs to prove to Bob she knows a set of coefficients for a polynomial
P(x)
- Bob wants to use a secret value s to challenge Alice
- Alice must not know the value s, Bob must not know P(x)
Alice Bob
A few more steps involved to complete the protocol:
- Homomorphic Hiding
- Blind Evaluation of Polynomials
- Convert to non-interactive using a Common Reference String
obtained from a Trusted Setup

31. Usage of ZKPs
● Digital Signatures (eg. ECDSA) is essentially a zero knowledge proof
of the knowledge of the private key

32. Usage of ZKPs
● Hide transaction payloads in a blockchain
○ Alice sends Bob 10 fungible tokens, by executing the transaction privately and
sends a ZKP of the tx
○ All validators in the blockchain network can see the zkp, and verify that the
transaction has been executed honestly, without knowing the details of the
transaction
○ zCash, EY Nightfall confidential token

33. Usage of ZKPs
● Layer-2 Scaling Solutions
○ ZKP is great at compressing a large amount of computation into a small proof that
can be verified fast
○ zkSync, Loopring, StarkNet, Polygon Hermez, etc.

34. Usage of ZKPs
● Self-Sovereign Identities
○ Presenting a claim about “are you over 21 years old to be admitted into the bar?”
without disclosing the birth date, but by using a ZKP

35. Where to Learn More
Best learning websites with curated content:
- https://learn.0xparc.org/
Step-by-Step Explanation of SNARK (without skipping the math):
- https://electriccoin.co/blog/snark-explain/
101 Level hands-on tutorials:
- https://github.com/privacy-scaling-explorations/zkp-app-boilerplate
Circuit Compiler & Proof Generation:
- https://github.com/iden3/circom
- https://github.com/iden3/snarkjs