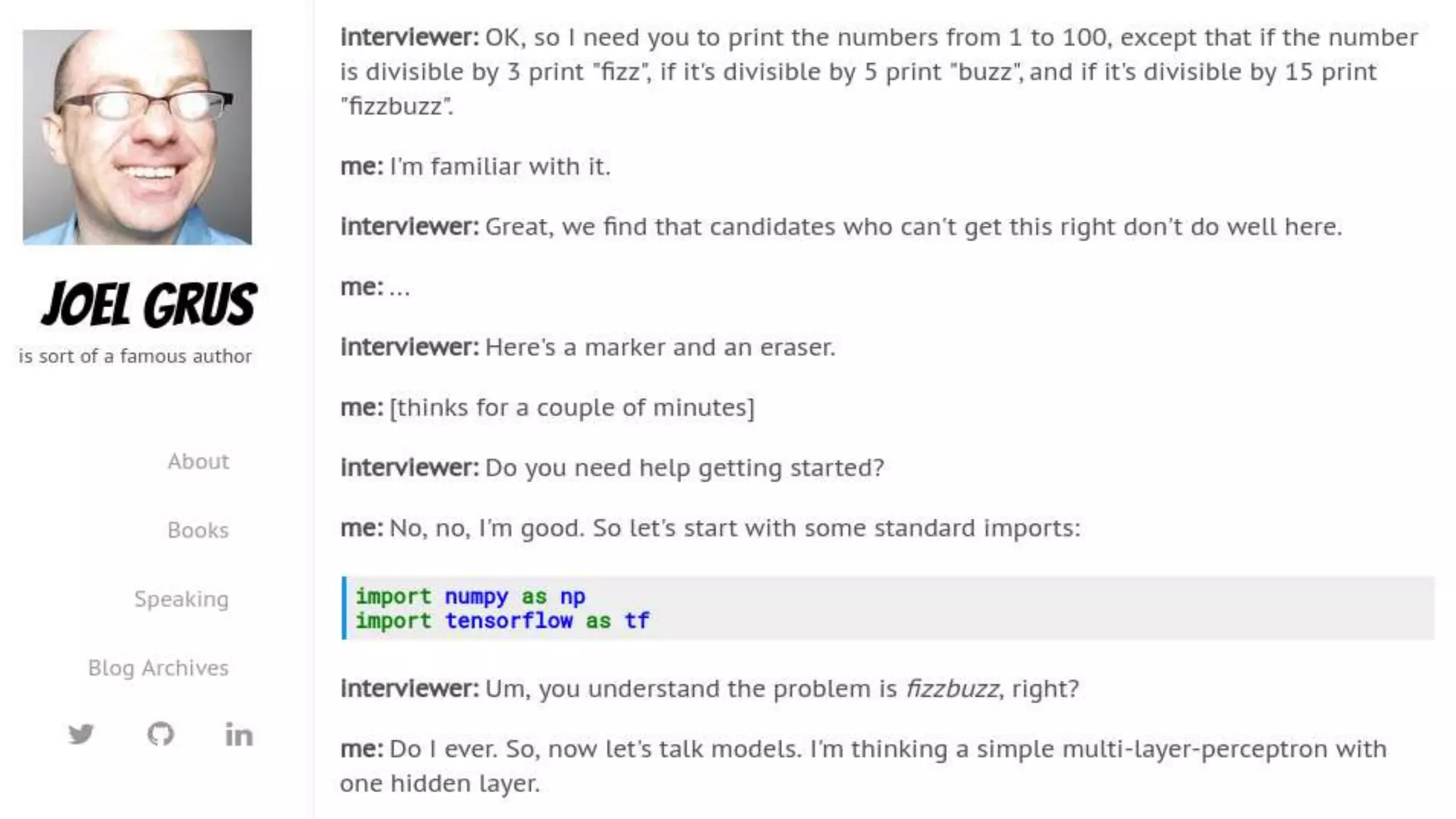
This document discusses using machine learning to solve the "Fizz Buzz" problem in an unconventional way. The author first presents simple Python solutions to Fizz Buzz. He then frames Fizz Buzz as a classification problem, where the goal is to predict the correct "Fizz", "Buzz", "FizzBuzz", or number output given an input number. Various machine learning models are applied to this problem, including linear regression, logistic regression, multilayer perceptrons, and deep learning models. The author finds that deeper neural networks can reliably solve Fizz Buzz after training.

1. Fizz buzz in tensorflow
Joel Grus
Research Engineer, AI2
@joelgrus

3. About me
Research engineer at AI2
we're hiring!
(in Seattle)
(where normal people can afford to buy a house)
(sort of)
Previously SWE at Google, data science at
VoloMetrix, Decide, Farecast/Microsoft
Wrote a book ------->

4. Fizz Buzz, in case you're not familiar
Write a program that prints the numbers 1 to 100, except that
if the number is divisible by 3, instead print "fizz"
if the number is divisible by 5, instead print "buzz"
if the number is divisible by 15, instead print "fizzbuzz"

5. weed-out problem

7. the backstory
Saw an online discussion about the stupidest way to solve fizz buzz
Thought, "I bet I can come up with a stupider way"
Came up with a stupider way
Blog post went viral
Sort of a frivolous thing to use up my 15 minutes of fame on, but so
be it

10. super simple solution
haskell
fizzBuzz :: Integer -> String
fizzBuzz i
| i `mod` 15 == 0 = "fizzbuzz"
| i `mod` 5 == 0 = "buzz"
| i `mod` 3 == 0 = "fizz"
| otherwise = show i
mapM_ (putStrLn . fizzBuzz) [1..100]
ok, then python
def fizz_buzz(i):
if i % 15 == 0: return "fizzbuzz"
elif i % 5 == 0: return "buzz"
elif i % 3 == 0: return "fizz"
else: return str(i)
for i in range(1, 101):
print(fizz_buzz(i))

11. taking on
fizz buzz as a
machine
learning problem

12. outputs
given a number, there are four mutually exclusive cases
1.output the number itself
2.output "fizz"
3.output "buzz"
4.output "fizzbuzz"
so one natural representation of the output is a vector of length 4
representing the predicted probability of each case

13. ground truth
def fizz_buzz_encode(i):
if i % 15 == 0: return np.array([0, 0, 0, 1])
elif i % 5 == 0: return np.array([0, 0, 1, 0])
elif i % 3 == 0: return np.array([0, 1, 0, 0])
else: return np.array([1, 0, 0, 0])

14. feature selection - Cheating

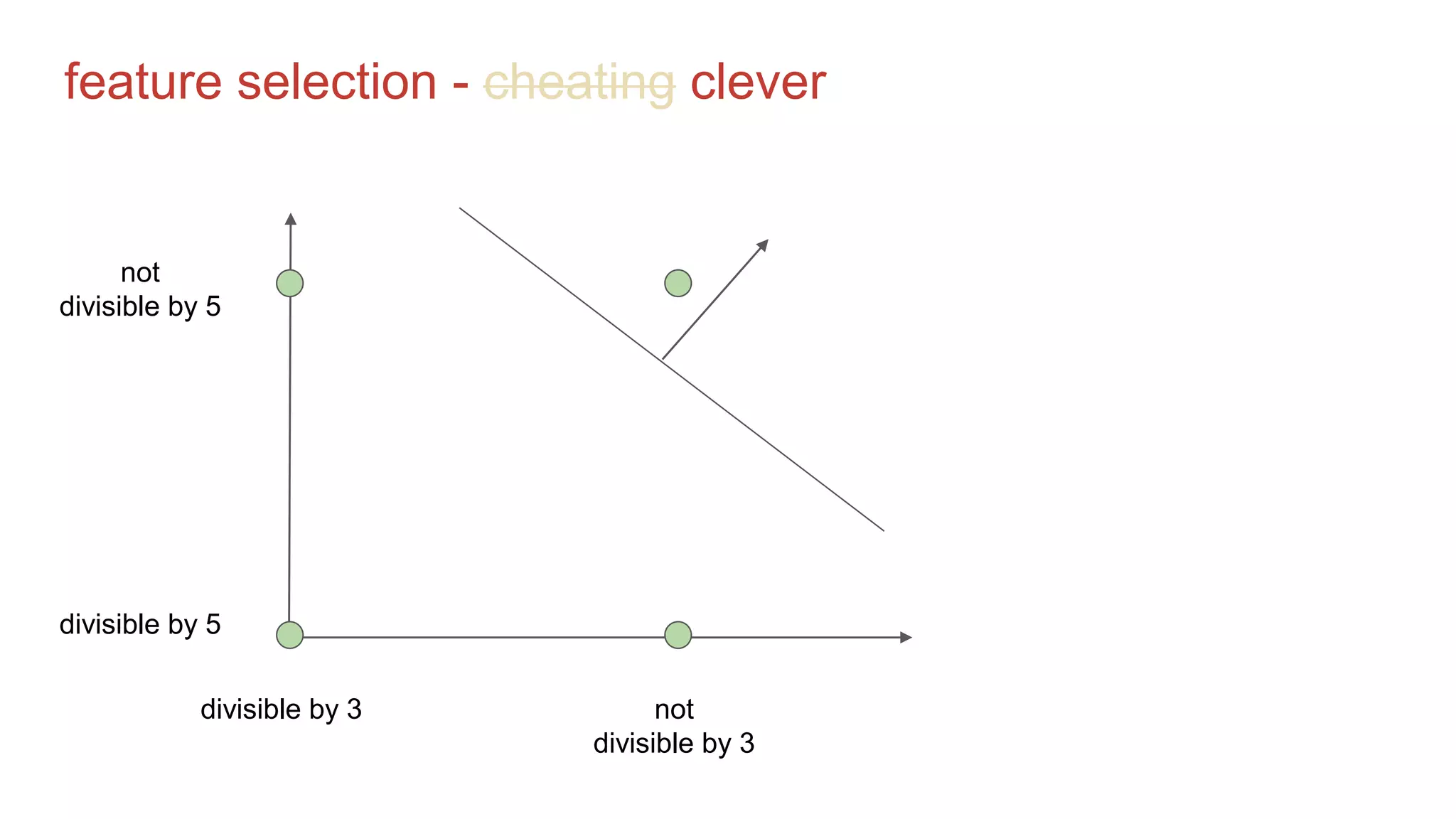
16. feature selection - cheating clever
def x(i):
return np.array([1, i % 3 == 0, i % 5 == 0])
def predict(x):
return np.dot(x, np.array([[ 1, 0, 0, -1],
[-1, 1, -1, 1],
[-1, -1, 1, 1]]))
for i in range(1, 101):
prediction = np.argmax(predict(x(i)))
print([i, "fizz", "buzz", "fizzbuzz"][prediction])
It's hard to
imagine an
interviewer
who wouldn't
be impressed
by even this
simple
solution.

17. feature selection - cheating clever
divisible by 3 not
divisible by 3
divisible by 5
not
divisible by 5

18. what if we aren't that clever?
binary encoding, say 10
digits (up to 1023)
1 -> [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2 -> [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
3 -> [1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
and so on
in comments, someone
suggested one-hot decimal
encoding the digits, say up to
999
315 -> [0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
and so on

19. training data
need to generate fizz buzz for 1 to 100, so don't want to train
on those
binary: train on 101 - 1023
one-hot decimal digits: train on 101 - 999
then use 1 to 100 as the test data

20. tensorflow in one slide
import numpy as np
import tensorflow as tf
X = tf.placeholder("float", [None, input_dim])
Y = tf.placeholder("float", [None, output_dim])
beta = tf.Variable(tf.random_normal(beta_shape, stddev=0.01))
def model(X, beta):
# some function of X and beta
p_yx = model(X, beta)
cost = some_cost_function(p_yx, Y)
train_op = tf.train.SomeOptimizer.minimize(cost)
with tf.Session() as sess:
sess.run(tf.initialize_all_variables())
for _ in range(num_epochs):
sess.run(train_op, feed_dict={X: trX, Y: trY})
the extent of what I know
about
standard
imports
placeholders for our
data
parameters to
learn
some parametric
model
applied to the symbolic
variables
train by minimizing some cost
function
create session and initialize
variables
train using
data

21. Visualizing the results (a hard problem by itself)
1 100correct "11"
incorrect "buzz"
actual "fizzbuzz"
correct "fizz"
black + red = predictions
black + tan = actuals
predicted "fizz"
actual "buzz"
[[30, 11, 6, 2],
[12, 8, 4, 1],
[ 4, 3, 2, 3],
[ 4, 2, 0, 0]]

22. linear regression
def model(X, w, b):
return tf.matmul(X, w) + b
py_x = model(data.X, w, b)
cost = tf.reduce_mean(tf.pow(py_x - data.Y, 2))
train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost)
binary
decimal
[[54, 27, 14, 6],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0]]
[[54, 27, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 14, 6],
[ 0, 0, 0, 0]]
black + red = predictions
black + tan = actuals

23. logistic regression
def model(X, w, b):
return tf.matmul(X, w) + b
py_x = model(data.X, w, b)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(py_x, data.Y))
train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost)
binary
[[54, 27, 14, 6],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0]]
[[54, 27, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 14, 6],
[ 0, 0, 0, 0]]
decimal
black + red = predictions
black + tan = actuals

24. multilayer perceptron
def model(X, w_h, w_o, b_h, b_o):
h = tf.nn.relu(tf.matmul(X, w_h) + b_h) # 1 hidden layer with ReLU
activation
return tf.matmul(h, w_o) + b_o
py_x = model(data.X, w_h, w_o, b_h, b_o)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(py_x, data.Y))
train_op = tf.train.RMSPropOptimizer(learning_rate=0.0003,
decay=0.8,
momentum=0.4).minimize(cost)
from here on, no more decimal encoding, it's
really good at "divisible by 5" and really bad at

25. by # of hidden units (after 1000's of epochs)
5
10
25
50
100
200
[[52, 2, 1, 0],
[ 0, 25, 0, 0],
[ 1, 0, 13, 0],
[ 0, 0, 0, 6]]
[[45, 16, 3, 0],
[ 8, 11, 1, 0],
[ 0, 0, 10, 0],
[ 0, 0, 0, 6]]
black + red = predictions
black + tan = actuals

26. deep learning
def model(X, w_h1, w_h2, w_o, b_h1, b_h2, b_o, keep_prob):
h1 = tf.nn.dropout(tf.nn.relu(tf.matmul(X, w_h1) + b_h1), keep_prob)
h2 = tf.nn.relu(tf.matmul(h1, w_h2) + b_h2)
return tf.matmul(h2, w_o) + b_o
def py_x(keep_prob):
return model(data.X, w_h1, w_h2, w_o, b_h1, b_h2, b_o, keep_prob)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(py_x(keep_prob=0.5),
data.Y))
train_op = tf.train.RMSPropOptimizer(learning_rate=0.0003, decay=0.8,
momentum=0.4).minimize(cost)
predict_op = tf.argmax(py_x(keep_prob=1.0), 1)

27. HIDDEN LAYERS (50% dropout in 1st hidden layer)
[100, 100]
will sometimes get it 100% right, but not reliably
[2000, 2000]
seems to get it exactly right every time (in ~200 epochs)
black + red = predictions
black + tan = actuals

28. But how does it work?
25-hidden-neuron shallow net was simplest interesting model
in particular, it gets all the "divisible by 15" exactly right
not obvious to me how to learn "divisible by 15" from binary
[[45, 16, 3, 0],
[ 8, 11, 1, 0],
[ 0, 0, 10, 0],
[ 0, 0, 0, 6]]
black + red = predictions
black + tan = actuals

29. which inputs produce largest "fizz buzz" values?
(120, array([ -4.51552565, -11.66495565, -17.10086776, 0.32237191])),
(240, array([ -5.04136949, -12.02974626, -17.35017639, 0.07112655])),
(90, array([ -4.52364648, -11.48799399, -16.91179542, -0.20747044])),
(465, array([ -4.95231711, -11.88604214, -17.5155363 , -0.34996536])),
(210, array([ -5.04364677, -11.85627498, -17.17183826, -0.4049097 ])),
(720, array([ -4.98066528, -11.68684173, -17.01117473, -0.46671827])),
(345, array([ -4.49738021, -11.34621705, -16.88004503, -0.4713167 ])),
(600, array([ -4.48999048, -11.30909995, -16.70980522, -0.53889132])),
(360, array([ -9.32991992, -15.18924931, -17.8993147 , -4.35817601])),
(480, array([ -9.79430086, -15.72038142, -18.51560547, -4.38727747])),
(450, array([ -9.80194752, -15.54985676, -18.32664509, -4.89815184])),
(330, array([ -9.34660544, -15.01537882, -17.69651957, -4.95658813])),
(960, array([ -9.74109305, -15.37921101, -18.16552369, -4.95677615])),
(840, array([ -9.31266483, -14.83212949, -17.49181923, -5.26606825])),
(105, array([ -8.73320381, -11.08279653, -9.31921242, -5.52620068])),
(225, array([ -9.22702329, -11.50045288, -9.64725618, -5.76014854])),
(585, array([ -8.62907369, -10.84616688, -9.23592859, -5.79517941])),
(705, array([ -9.12030976, -11.2651869 , -9.56738927, -6.02974533])),
last column only needs
to be larger than the
other columns but in
this case it works out --
these are all divisible
by 15
notice that they cluster
into similar outputs
notice also that we
have pairs of numbers
that differ by 120

30. a stray observation
If two numbers differ by a multiple of 15, they have the same
fizz buzz output
If a network could ignore differences that are multiples of 15 (or
30, or 45, or so on), that could be a good start
Then only have to learn the correct output for each equivalence
class
Very few "fizz buzz" equivalence classes

31. two-bit SWAPS that are congruent mod 15
-8 +128 = +120
120 [0 0 0 1 1 1 1 0 0 0]
240 [0 0 0 0 1 1 1 1 0 0]
+2 -32 = -30 (from 120/240)
90 [0 1 0 1 1 0 1 0 0 0]
210 [0 1 0 0 1 0 1 1 0 0]
-32 +512 = +480 (from 120/240)
600 [0 0 0 1 1 0 1 0 0 1]
720 [0 0 0 0 1 0 1 1 0 1]
+1 -256 = -255 (from 600/720)
345 [1 0 0 1 1 0 1 0 1 0]
465 [1 0 0 0 1 0 1 1 1 0]

32. two-bit SWAPS that are congruent mod 15
-8 +128 = +120
120 [0 0 0 1 1 1 1 0 0 0]
240 [0 0 0 0 1 1 1 1 0 0]
+2 -32 = -30
90 [0 1 0 1 1 0 1 0 0 0]
210 [0 1 0 0 1 0 1 1 0 0]
-32 +512 = +480
600 [0 0 0 1 1 0 1 0 0 1]
720 [0 0 0 0 1 0 1 1 0 1]
+1 -256 = -255
345 [1 0 0 1 1 0 1 0 1 0]
465 [1 0 0 0 1 0 1 1 1 0]
-8 +128
360 [0 0 0 1 0 1 1 0 1 0]
480 [0 0 0 0 0 1 1 1 1 0]
330 [0 1 0 1 0 0 1 0 1 0]
450 [0 1 0 0 0 0 1 1 1 0]
840 [0 0 0 1 0 0 1 0 1 1]
960 [0 0 0 0 0 0 1 1 1 1]

33. two-bit SWAPS that are congruent mod 15
-8 +128 = +120
120 [0 0 0 1 1 1 1 0 0 0]
240 [0 0 0 0 1 1 1 1 0 0]
+2 -32 = -30
90 [0 1 0 1 1 0 1 0 0 0]
210 [0 1 0 0 1 0 1 1 0 0]
-32 +512 = +480
600 [0 0 0 1 1 0 1 0 0 1]
720 [0 0 0 0 1 0 1 1 0 1]
+1 -256 = -255
345 [1 0 0 1 1 0 1 0 1 0]
465 [1 0 0 0 1 0 1 1 1 0]
-8 +128
360 [0 0 0 1 0 1 1 0 1 0]
480 [0 0 0 0 0 1 1 1 1 0]
330 [0 1 0 1 0 0 1 0 1 0]
450 [0 1 0 0 0 0 1 1 1 0]
840 [0 0 0 1 0 0 1 0 1 1]
960 [0 0 0 0 0 0 1 1 1 1]
105 [1 0 0 1 0 1 1 0 0 0]
225 [1 0 0 0 0 1 1 1 0 0]
-32 +512
585 [1 0 0 1 0 0 1 0 0 1]
705 [1 0 0 0 0 0 1 1 0 1]
any neuron with the same weight on those
two inputs will produce the same outcome
if they're swapped
if you want to drive yourself mad, spend a
few hours staring at the neuron weights
themselves!

34. lessons learned
It's hard to turn a joke blog post into a talk
Feature selection is important (we already knew that)
Stupid problems sometimes contain really interesting
subtleties
Sometimes "black box" models actually reveal those
subtleties if you look at them the right way

35. sorry for
not being
just a joke
talk!

36. thanks!
code: github.com/joelgrus
blog: joelgrus.com
twitter: @joelgrus
(will tweet out link to slides, so go follow!)
book: --------------------------->
(might add a chapter about slides, so go
buy just in case!)