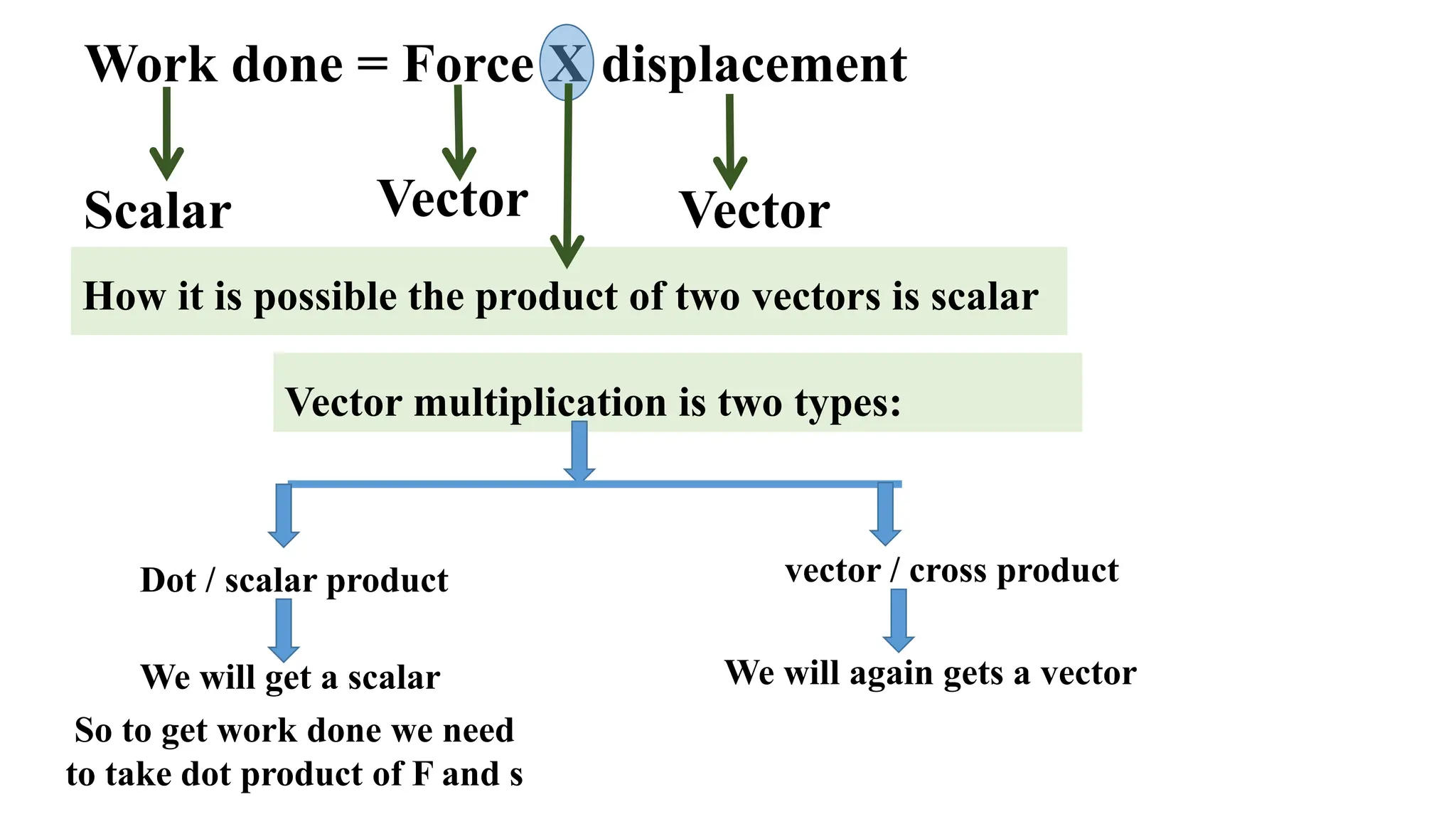
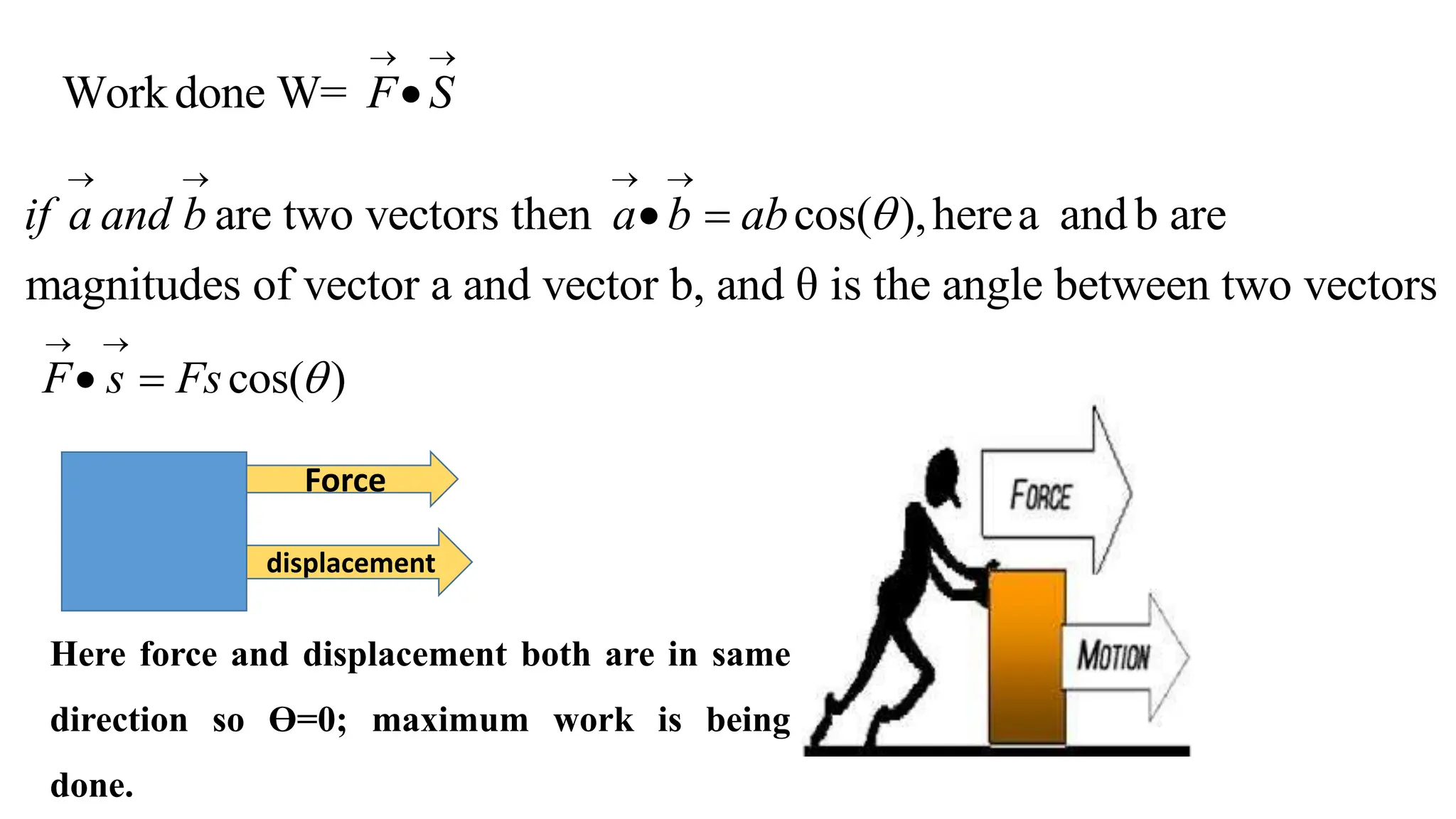
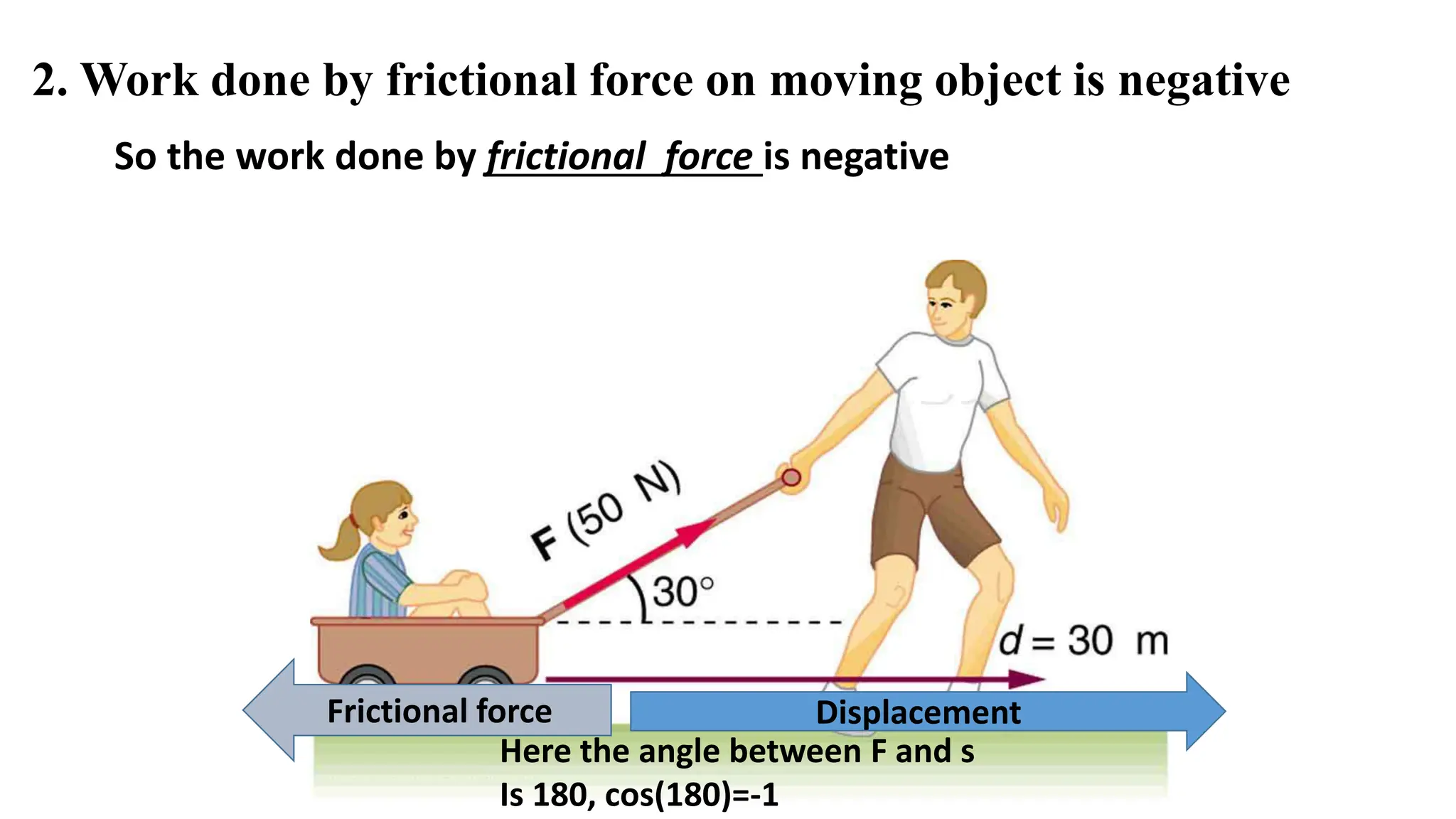
The document explains the concepts of work, energy, and power, detailing how work is defined as the product of force and displacement, with specific conditions for its calculation. It discusses the different types of potential energy and how the angle between force and displacement affects work done, categorizing it into positive, negative, and zero work. Additionally, it highlights the relationship between units of work in the SI system and describes various examples illustrating these principles.

1. Work, Energy and Power

2. Who are doing work?

3. Who are doing
work?

4. F-FORCE
d- displacement
In this case the work is being done
Work is said to be done when a force is applied on a body and the body
moves in the direction of force or in opposite direction
(Or) Work is said to be done when a force on a body produces displacement
in it. Work = Force x Displacement

5. Two important conditions for the work to be done are:-
1. A force must be applied
2. The object must be displaced. ( In the direction of force or opposite
direction)
Work done depends on:-
1. Magnitude of force
2. Displacement of the body.

6. How it is possible the product of two vectors is scalar
Work done = Force X displacement
Vector Vector
Scalar
Vector multiplication is two types:
Dot / scalar product vector / cross product
We will get a scalar We will again gets a vector
So to get work done we need
to take dot product of F and s

7. Workdone W= F S
 

are two vectors then cos( ),herea andb are
magnitudes of vector a and vector b, and θ is the angle between two vectors
if a and b a b ab 
   
 
cos( )
F s Fs 
 
 
Force
displacement
Here force and displacement both are in same
direction so Ө=0; maximum work is being
done.

8. Here force and displacement both are not in same
direction, but still there is a displacement. the angle
between them is Ө=30;
Here the total force F=50N will not act in the direction
of displacement( horizontal)
Now how to Find out the amount of force acting in
horizontal direction?

9. Force- F
Displacement- S
Ө
But total force will act in the direction of displacement, No
Any vector will have two components (x, y). X component is along horizontal, y component
acts in vertical direction.
Means to find out work done we need to find out x component/ horizontal component.
For that we will use trigonometric ratios.

10. Basic ratios in Trigonometry
• sine( sin)
• cosine (cos)
• tangent (tan)
• cotangent (cot)
• Secant( sec)
• Cosecant (cosec)
Opposite
Sin(θ) =
Hypotenuse
base
cos(θ) =
Hypotenuse
But here which trigonometric ratio we need to take?
θ
Opposite
side
Base
x- component of F
Here base x- component of F and cosine related to
each other. So we need to take cosine.

11. Angle(θ)
Cos(θ) 3
2
2 1
2 2
or
1
2
0⁰
1
30⁰ 45⁰ 60⁰ 90⁰
0
180⁰
-1

12. Work done by a horizontal force:
Force (F)
displacement(s)
Work done by a horizontal force W= F.s
W= F s cos(Ө)
Here F & S are in the same direction so Ө=0; and cos(0)=1;
W= F s
W= Force X displacement

13. Work done by a constant force acting obliquely:
displacement(s)
Work done by a horizontal force W= F.s
W= F s cos(Ө)
Here Ө is the angle between force and displacement
Ө

14. Units for work done:
In S.I. System the unit for Work done: N.m or J
In S.I. System the unit for Work done: dyne. cm or erg
Relation between Joule and erg:
1J=1N.1m
5 2
Here1N=10 dyne;1m=10 cm;
5 2
so1J=10 dyne×10 cm;
5 2
1J=10 ×10 dyne.cm;
7
1J=10 dyne.cm;weknow thatdyne.cm=1erg;
7
1J=10 erg

15. Types of work done:
Depending on the angle(θ) between force and displacement the work done can
be
1. Positive
2. Negative
3. Zero

16. 1. Positive
If the angle between force and displacement is greater than equal to 0 and
less than 90.
W= F S Cos(θ)
Cos(θ) value is positive if the angle (θ) 0 ≤ θ <90,
W is always positive , Cos(θ) value is positive

17. Example for Positive work done
Cos(θ) value is positive if the angle (θ) is in between 0 and 90, so here W is
always positive. Means if the object moves in the direction of force we can
that the work done is positive.
Examples for positive work:
FORCE
Displacement
1. While lift an object the work done by
The person is positive. Here the person
is applying force in up direction, and
The object also displaced in the same
Direction.

18. Force applied by horse
displacement
2. When we pull/ push an object the direction of force and the direction
displacement will be in same direction. In this the angle between force and
Displacement will be zero. So the work done is positive.

19. Here angle between F and S
Is less than 90 so W is positive.

20. 3. Work done by gravitational force on falling object.
Gravitational
force
displacement
Here the force and displacement are in same
Direction.

21. 2. Negative work done
If the angle between force and displacement is more than 90 and less than or
equal to 180, then work done will be negative.
W= F S Cos(θ)
Cos(θ) value is negative if the angle (θ) is 90 < θ ≤ 180,
W is always negative

22. 1. Work done by gravitational force on a ball thrown
vertically up.
Gravitational
force
displacement
Here the angle between F and s
Is 180, cos(180)=-1
So the work done by gravitational force is negative

23. 2. Work done by frictional force on moving object is negative
Here the angle between F and s
Is 180, cos(180)=-1
So the work done by frictional force is negative
Frictional force Displacement

24. When brakes are applied
Direction of motion/ displacement
Force applied by brakes
Here the angle between F and s
Is 180, cos(180)=-1

25. Zero work done
The work done is
If
• force is zero
• displacement is zero
• Angle between force and displacement is 90 or
270.

26. Examples for zero work done
The work done is zero.
If force is applied
But displacement is zero

28. The work done
In lifting the weights is_______________
In holding the weights is_____________

29. The work done
Work done in lifting the bag
is______________
Work done in moving by holding
the bag is_____________
Work done in holding the bag
is_____________

30. Work done by centripetal force:
• Centripetal force acts along the radius
and towards the centre
• Direction of motion is along the tangent
• Force and displacement are
perpendicular so Work done is zero

31. Energy
(E) is defined as the capacity to do work (scalar)

32. Potential Energy:
The energy possessed by a body by virtue of
• Its position
• Shape
• Size
“The energy possessed by a body by virtue of its position/ shape/ size is
called potential energy”.

33. Types potential Energy:
i. Elastic potential energy: The energy possessed by a body by virtue of
its shape
size
Elastic potential energy: The energy possessed by a body by virtue of its
shape/ size/ configuration is called elastic potential energy.

34. ii. Gravitational potential energy: The energy possessed by a body by
virtue of
its
position
Gravitational potential energy : The energy possessed by a body by
virtue of its position

35. iii. Electric potential energy:
Electric potential energy due to configuration of charge or because position of
charges from other charges.
+
+
To bring the charge near to other charge
We need to do work,
Whatever the workdone in bringing the
Charge stored as electric potential energy.

36. iv. Chemical potential energy :
The energy stored in chemicals.
Ex: petrol and other fuels