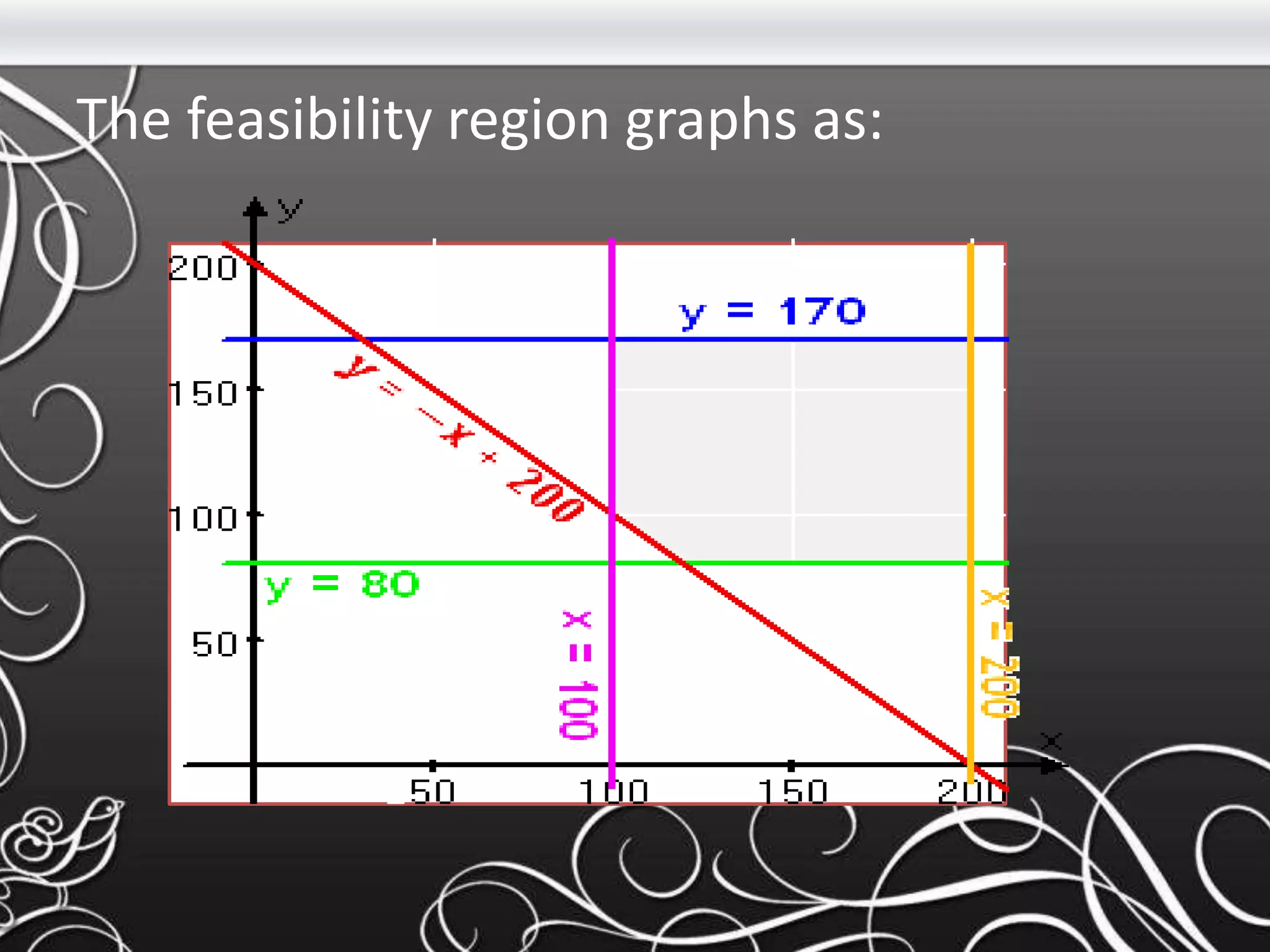
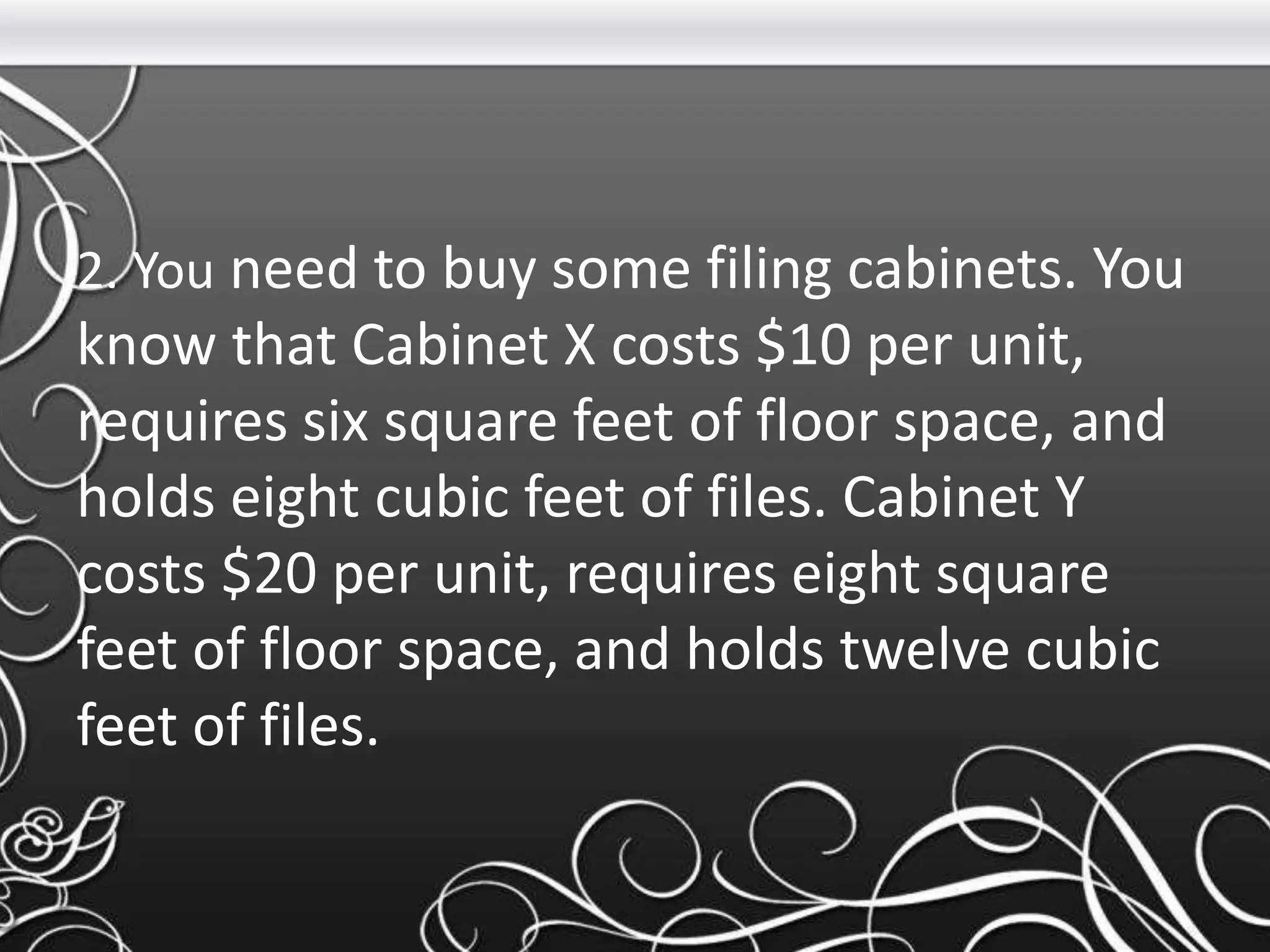
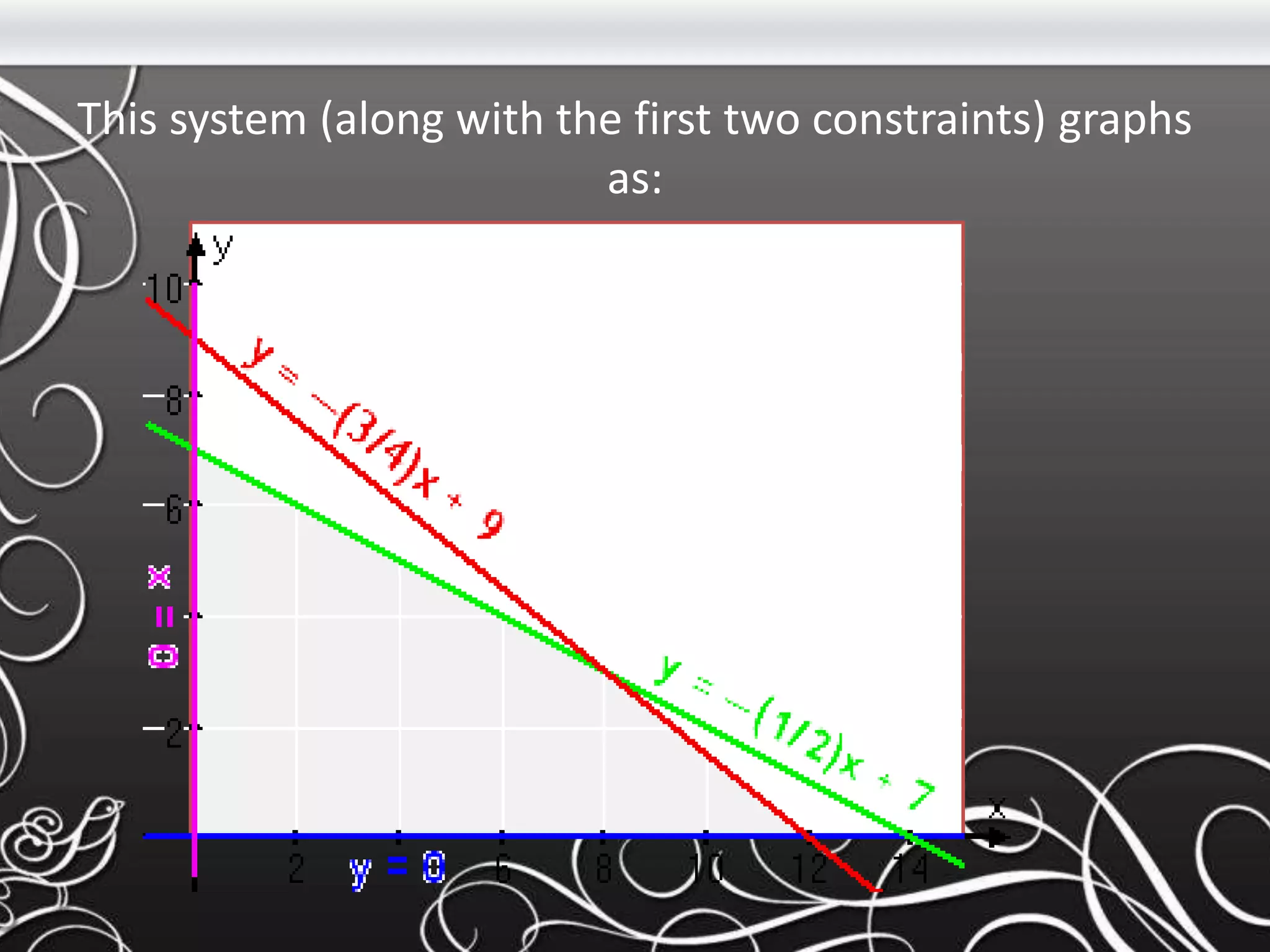
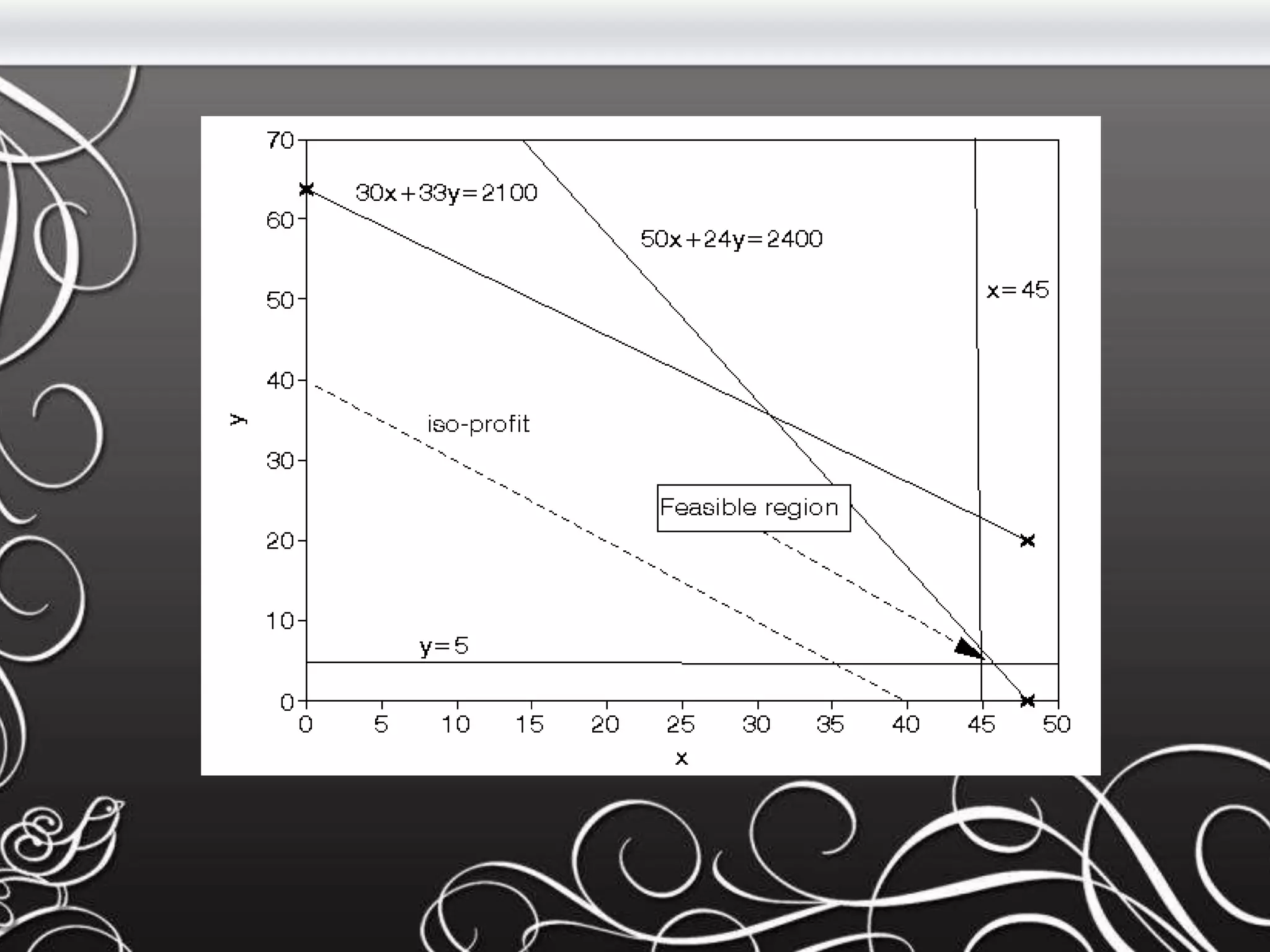
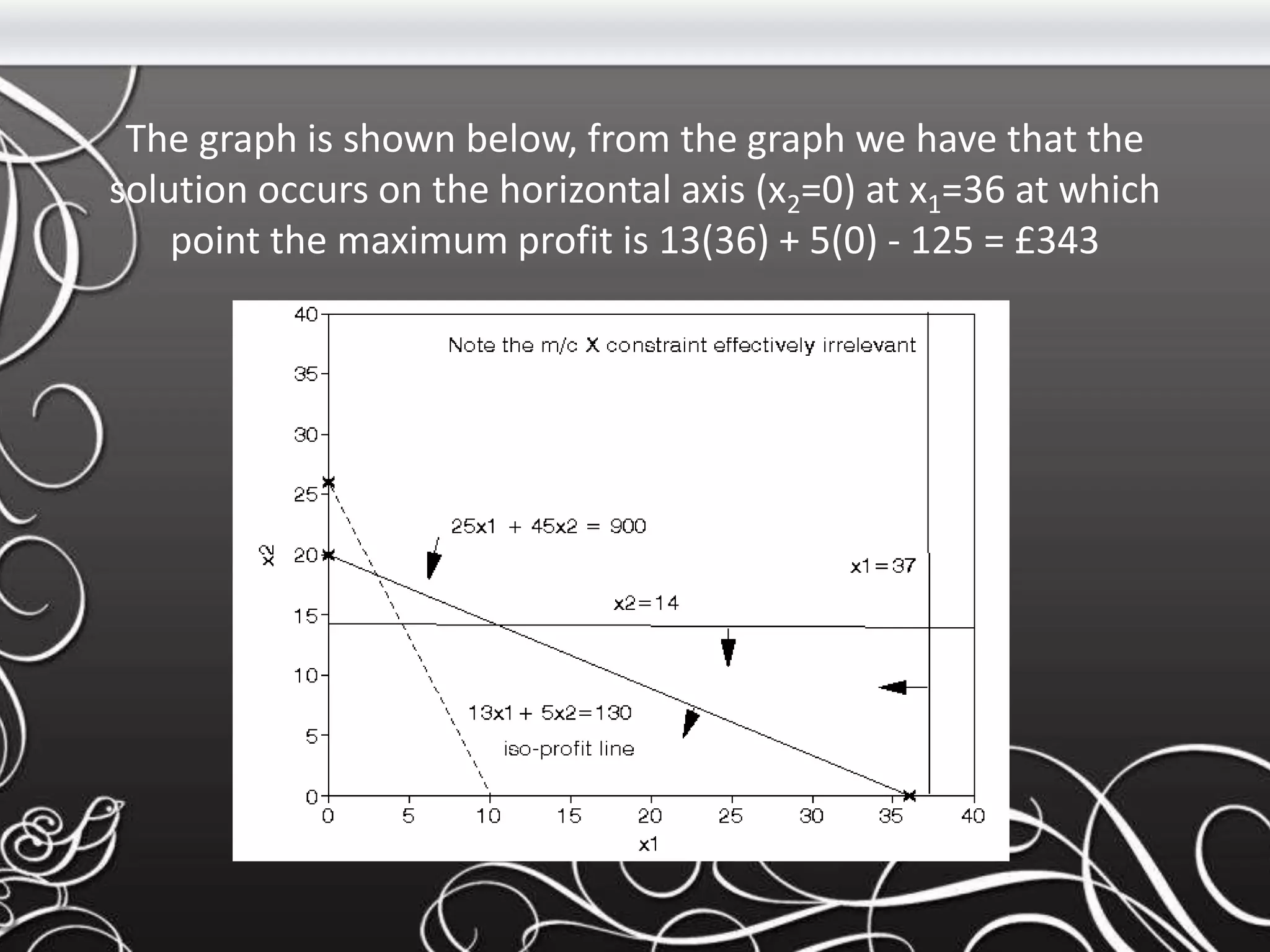
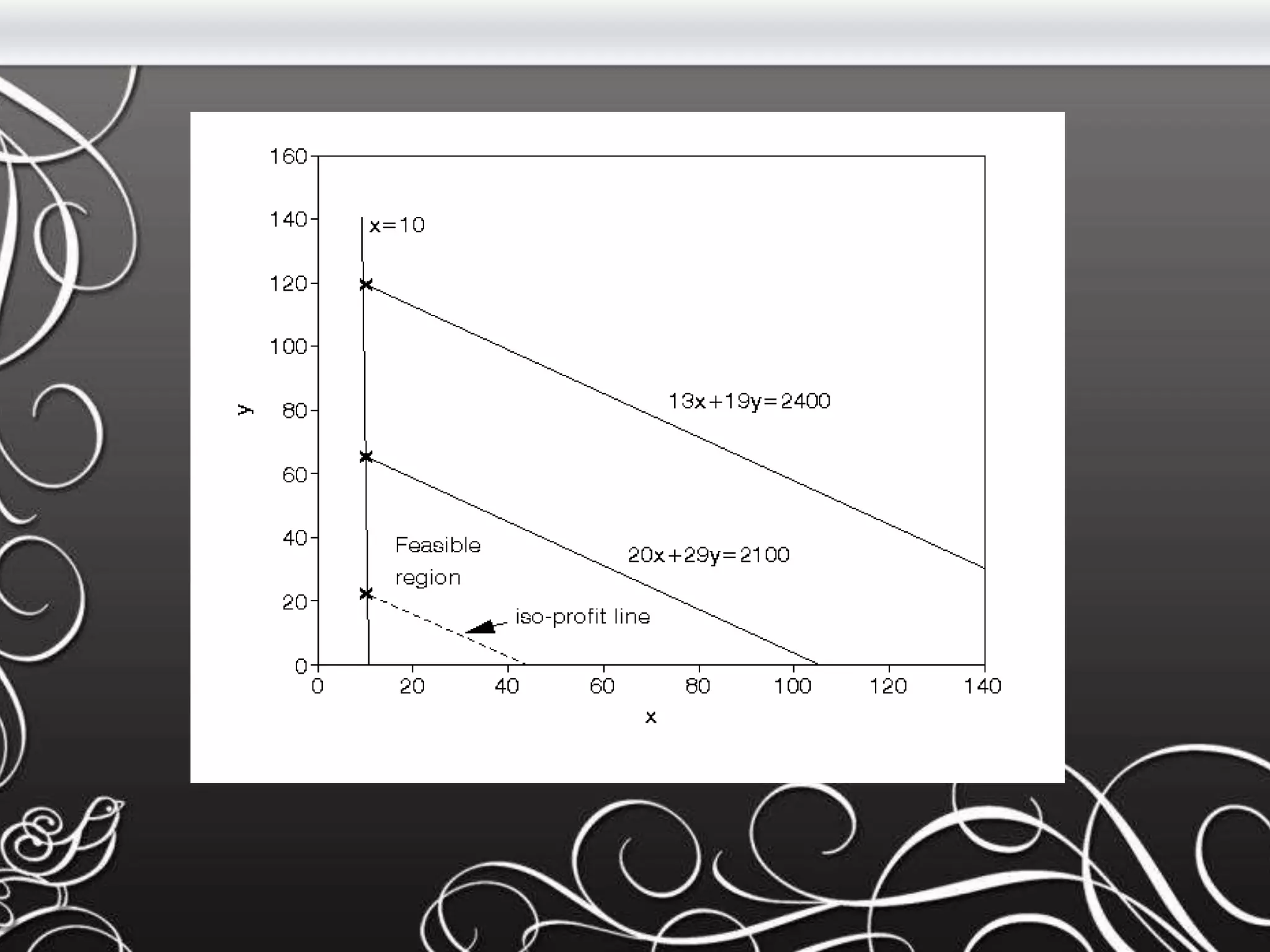
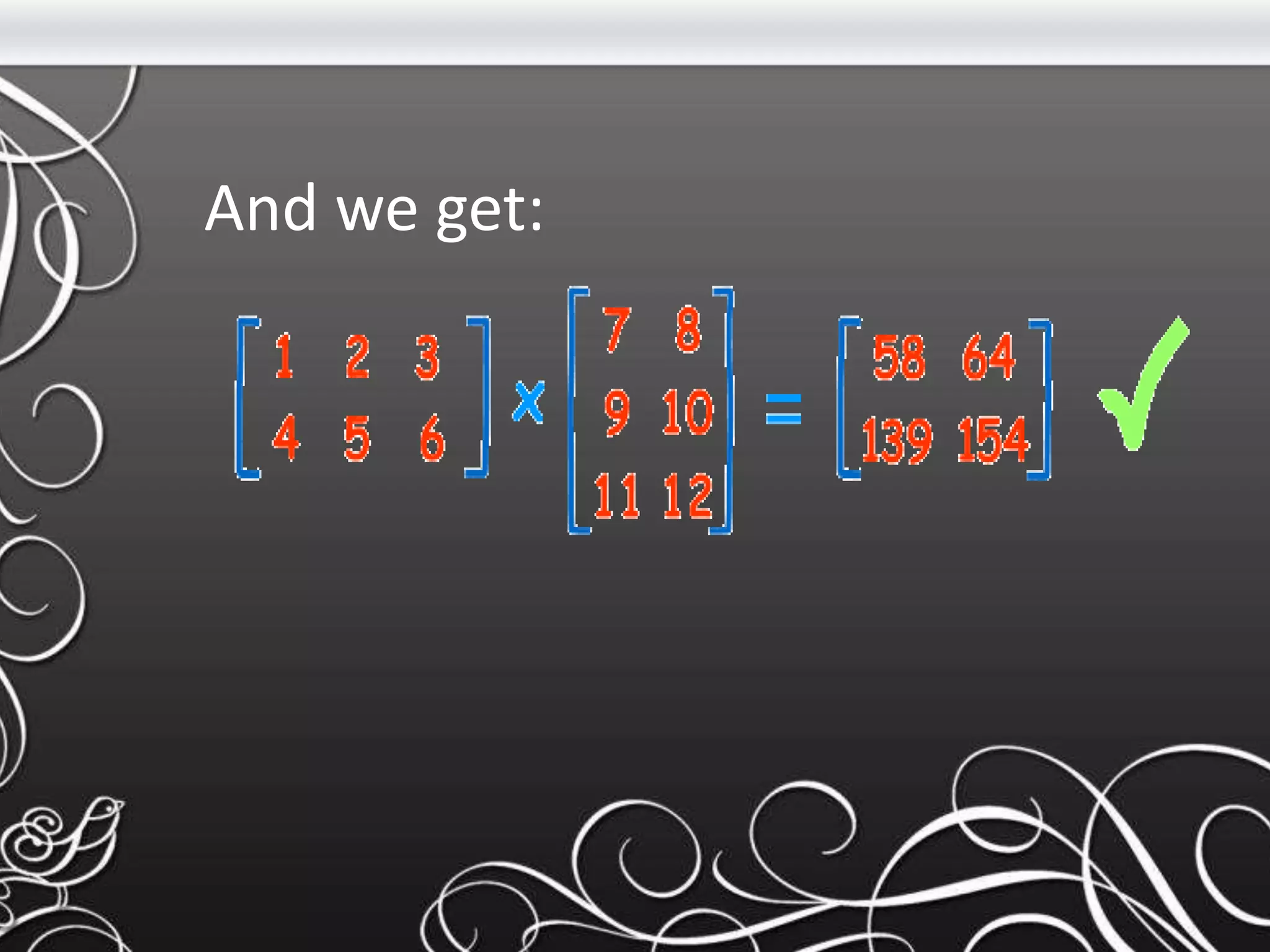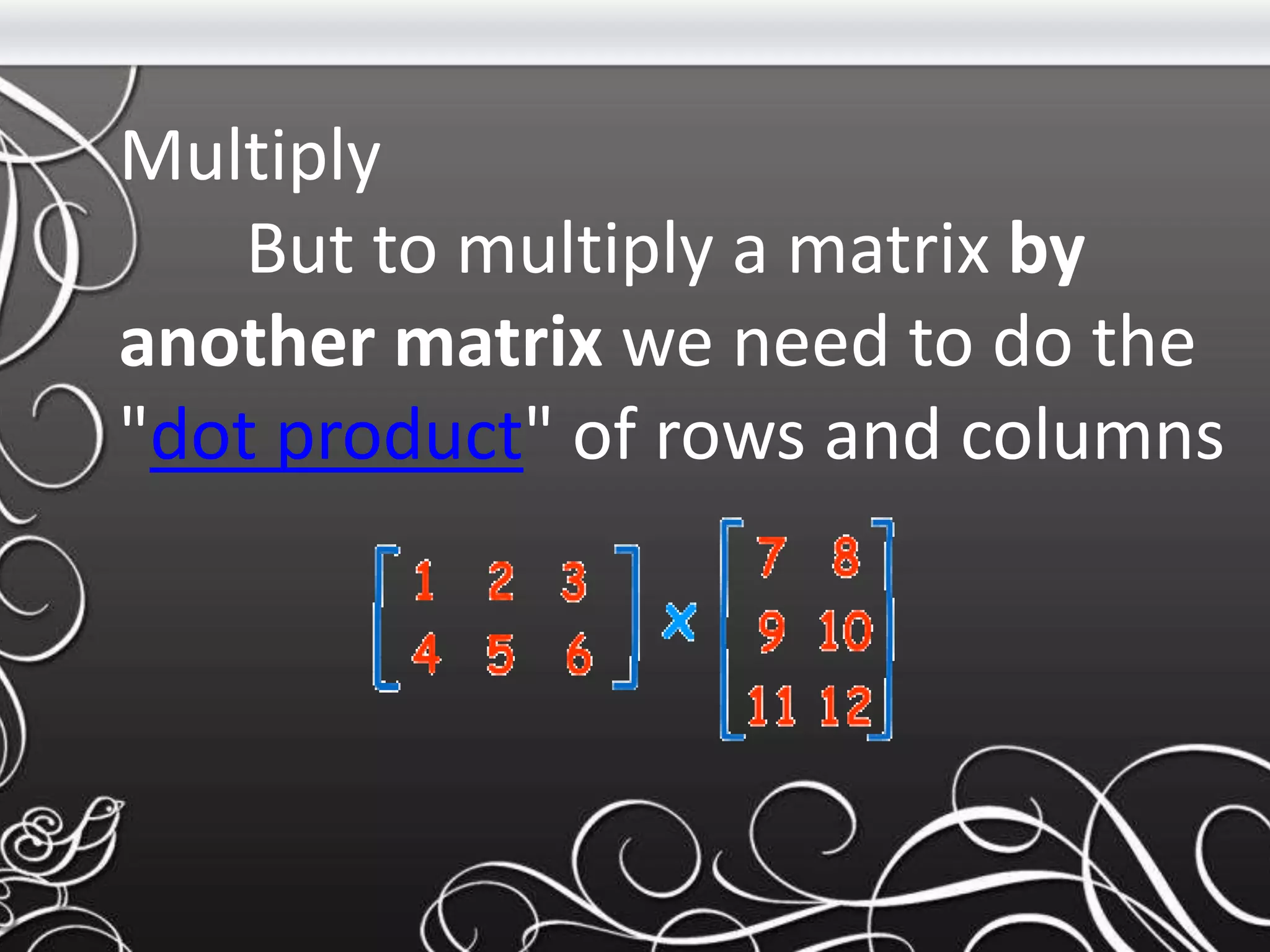
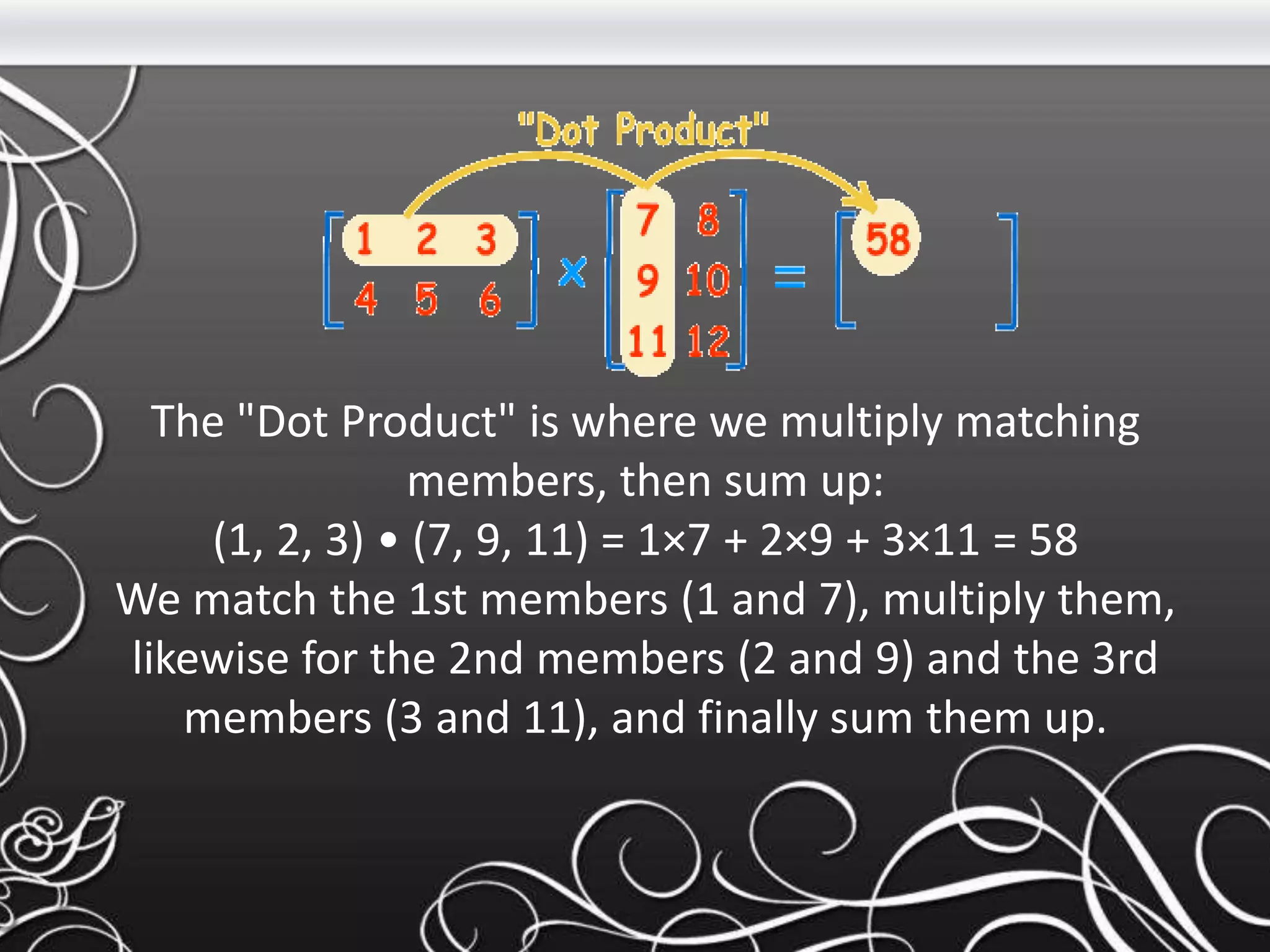
- The document discusses matrices, including definitions, operations, and examples of matrix addition, subtraction, transposition, and multiplication. It also covers linear programming, defining it as a method to optimize a mathematical model to achieve the best outcome. - Key concepts covered include the definitions of a matrix and its elements, how to perform basic operations like addition and subtraction on matrices, and how matrices are multiplied using the dot product of rows and columns. Linear programming is introduced as a method using linear relationships to find the maximum or minimum value of an objective function.

1. Management
Science

2.  Matrices
 Linear Programming

3. Matrix
is an ordered rectangular array
of numbers.
A Matrix
(This one has 2 Rows and 3 Columns)

4. A matrix is usually shown by a capital
letter (such as A, or B)
Each entry (or "element") is shown by
a lower case letter with a "subscript"
of row,column:

5. Rows and Columns
So which is the row and which is the
column?
Rows go left-right
Columns go up-down
To remember that rows come before
columns use the word "arc":
ar,c

6. Here are some sample entries:
b1,1 = 6 (the entry at row 1, column 1 is 6)
ar,c
b1,3 = 24 (the entry at row 1, column 3 is
24)
Example:

7. Addition
Two matrices A and B of the
same size can be added or to
produce a matrix of the same size.
3 8 4 0
4 6 1 -9

8. These are the calculations:
3+4=7 8+0=8
4+1=5 6+(-9)=-3

9. Subtraction
Two matrices C and D of the same
size can be subtracted or to produce a
matrix of the same size.
3 8 4 0
4 6 1 -9

10. These are the calculations:
3-4=-1 8-0=8
4-1=3 6-(-9)=15
Note: subtracting is actually defined
as the addition of a negative matrix:
A + (-B)

11. Tranpose of a Matrix
To "transpose" a matrix, swap
the rows and columns. We put a
"T" in the top right-hand corner to
mean transpose:

12. Multiply
But to multiply a matrix by
another matrix we need to do the
"dot product" of rows and columns

13. The "Dot Product" is where we multiply matching
members, then sum up:
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58
We match the 1st members (1 and 7), multiply them,
likewise for the 2nd members (2 and 9) and the 3rd
members (3 and 11), and finally sum them up.

14. (1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64
We can do the same thing for the 2nd
row and 1st column:
(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139
And for the 2nd row and 2nd column:
(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

15. And we get:

16. Exercises:

17. Compute
1- C + E
2- AB
3- A’
4- A(2B)
5- E – C

18. Linear programming
- (LP; also called linear optimization) is
a method to achieve the best outcome
(such as maximum profit or lowest
cost) in a mathematical model whose
requirements are represented
by linear relationships.

19. SOLUTION OF LINEAR PROGRAMMING
PROBLEMS
• THEOREM 1 If a linear programming problem has
a solution, then it must occur at a vertex, or
corner
• point, of the feasible set, S, associated with the
problem. Furthermore, if the objective function P
is
• optimized at two adjacent vertices of S, then it is
optimized at every point on the line segment
joining
• these two vertices, in which case there are
infinitely many solutions to the problem.

20. THEOREM 2
• Suppose we are given a linear programming problem
with a feasible set S and an objective
• function P = ax+by. Then,
• If S is bounded then P has both a maximum and
minimum value on S
• If S is unbounded and both a and b are nonnegative,
then P has a minimum value on S provided
• that the constraints defining S include the inequalities x≥
0 and y≥ 0.
• If S is the empty set, then the linear programming
problem has no solution; that is, P has neither
• a maximum nor a minimum value.

21. THE METHOD OF CORNERS
• Graph the feasible set (region), S.
• Find the EXACT coordinates of all vertices (corner
points) of S.
• Evaluate the objective function, P, at each vertex
• The maximum (if it exists) is the largest value of P
at a vertex. The minimum is the smallest value
• of P at a vertex. If the objective function is
maximized (or minimized) at two vertices, it is
• minimized (or maximized) at every point
connecting the two vertices

22. Examples:
1.
The question asks for the optimal number of
calculators, so my variables will stand for
that:
x: number of scientific calculators produced
y: number of graphing calculators produced

23. Since they can't produce negative
numbers of calculators, I have the two
constraints, x > 0 and y > 0. But in this
case, I can ignore these constraints,
because I already have
that x > 100 andy > 80.

24. The exercise also gives
maximums: x < 200 and y < 170. The
minimum shipping requirement gives
mex + y > 200; in other words, y > –x +
200. The profit relation will be my
optimization equation: P = –2x + 5y. So the
entire system is:
P = –2x + 5y, subject to:
100 < x < 200
80 < y < 170
y > –x + 200

25. The feasibility region graphs as:

26. When you test the corner points at (100,
170), (200, 170), (200, 80), (120, 80),
and (100, 100), you should obtain the
maximum value of P = 650 at (x, y) = (100,
170). That is, the solution is "100scientific
calculators and 170 graphing calculators".

27. 2. You need to buy some filing cabinets. You
know that Cabinet X costs $10 per unit,
requires six square feet of floor space, and
holds eight cubic feet of files. Cabinet Y
costs $20 per unit, requires eight square
feet of floor space, and holds twelve cubic
feet of files.

28. You have been given $140 for this
purchase, though you don't have to spend
that much. The office has room for no
more than 72 square feet of cabinets.
How many of which model should you
buy, in order to maximize storage
volume?

29. The question ask for the number of
cabinets I need to buy, so my variables will
stand for that:
x: number of model X cabinets purchased
y: number of model Y cabinets purchased

30. Naturally, x > 0 and y > 0. I have to consider
costs and floor space (the "footprint" of
each unit), while maximizing the storage
volume, so costs and floor space will be my
constraints, while volume will be my
optimization equation.
cost: 10x + 20y < 140, or y < –( 1/2 )x + 7
space: 6x + 8y < 72, or y < –( 3/4 )x + 9
volume: V = 8x + 12y

31. This system (along with the first two constraints) graphs
as:

32. When you test the corner points at (8, 3),
(0, 7), and (12, 0), you should obtain a
maximal volume of100 cubic feet by buying
eight of model X and three of model Y.

33. 3. A company makes two products (X
and Y) using two machines (A and B).
Each unit of X that is produced requires
50 minutes processing time on machine
A and 30 minutes processing time on
machine B. Each unit of Y that is
produced requires 24 minutes
processing time on machine A and 33
minutes processing time on machine B.

34. At the start of the current week there are
30 units of X and 90 units of Y in stock.
Available processing time on machine A is
forecast to be 40 hours and on machine B
is forecast to be 35 hours.

35. The demand for X in the current week is
forecast to be 75 units and for Y is forecast
to be 95 units. Company policy is to
maximise the combined sum of the units of
X and the units of Y in stock at the end of
the week.

36. • Formulate the problem of deciding how
much of each product to make in the
current week as a linear program.
• Solve this linear program graphically.

37. Solution:
Let
• x be the number of units of X produced
in the current week
• y be the number of units of Y produced
in the current week

38. then the constraints are:
50x + 24y <= 40(60) machine A time
30x + 33y <= 35(60) machine B time
x >= 75 - 30
i.e. x >= 45 so production of X >= demand (75)
- initial stock (30), which ensures we meet
demand
y >= 95 - 90
i.e. y >= 5 so production of Y >= demand (95) -
initial stock (90), which ensures we meet
demand

39. • The objective is: maximise (x+30-75) + (y+90-
95) = (x+y-50)
i.e. to maximise the number of units left in
stock at the end of the week
• It is plain from the diagram below that the
maximum occurs at the intersection of x=45
and 50x + 24y = 2400

41. Solving simultaneously, rather than by
reading values off the graph, we have that
x=45 and y=6.25 with the value of the
objective function being 1.25

42. 4. The demand for two products in each of
the last four weeks is shown below.
Week
1 2 3 4
Demand - product 1 23 27 34 40
Demand - product 2 11 13 15 14

43. Apply exponential smoothing with a smoothing
constant of 0.7 to generate a forecast for the
demand for these products in week 5.
These products are produced using two
machines, X and Y. Each unit of product 1 that is
produced requires 15 minutes processing
onmachine X and 25 minutes processing on
machine Y. Each unit of product 2 that is
produced requires 7 minutes processing on
machine X and 45 minutes processing on
machine Y.

44. The available time on machine X in week 5 is
forecast to be 20 hours and on machine Y in
week 5 is forecast to be 15 hours. Each unit of
product 1 sold in week 5 gives a contribution to
profit of £10 and each unit of product 2 sold in
week 5 gives a contribution to profit of £4.

45. It may not be possible to produce enough to
meet your forecast demand for these products
in week 5 and each unit of unsatisfied demand
for product 1 costs £3, each unit of unsatisfied
demand for product 2 costs £1.
Formulate the problem of deciding how much of
each product to make in week 5 as a linear
program.
Solve this linear program graphically.

46. Solution
Note that the first part of the question is
a forecasting question so it is solved below.
For product 1 applying exponential smoothing with
a smoothing constant of 0.7 we get:
M1 = Y1 = 23
M2 = 0.7Y2 + 0.3M1 = 0.7(27) + 0.3(23) = 25.80
M3 = 0.7Y3 + 0.3M2 = 0.7(34) + 0.3(25.80) = 31.54
M4 = 0.7Y4 + 0.3M3 = 0.7(40) + 0.3(31.54) = 37.46
The forecast for week five is just the average for
week 4 = M4 = 37.46 = 31 (as we cannot have
fractional demand).

47. For product 2 applying exponential smoothing with
a smoothing constant of 0.7 we get:
M1 = Y1 = 11
M2 = 0.7Y2 + 0.3M1 = 0.7(13) + 0.3(11) = 12.40
M3 = 0.7Y3 + 0.3M2 = 0.7(15) + 0.3(12.40) = 14.22
M4 = 0.7Y4 + 0.3M3 = 0.7(14) + 0.3(14.22) = 14.07
The forecast for week five is just the average for
week 4 = M4 = 14.07 = 14 (as we cannot have
fractional demand).
We can now formulate the LP for week 5 using the
two demand figures (37 for product 1 and 14 for
product 2) derived above.

48. Let
x1 be the number of units of product 1 produced
x2 be the number of units of product 2 produced
where x1, x2>=0
The constraints are:
15x1 + 7x2 <= 20(60) machine X
25x1 + 45x2 <= 15(60) machine Y
x1 <= 37 demand for product 1
x2 <= 14 demand for product 2
The objective is to maximise profit, i.e.
maximise 10x1 + 4x2 - 3(37- x1) - 1(14-x2)
i.e. maximise 13x1 + 5x2 - 125

49. The graph is shown below, from the graph we have that the
solution occurs on the horizontal axis (x2=0) at x1=36 at which
point the maximum profit is 13(36) + 5(0) - 125 = £343

50. 5. A company is involved in the production of
two items (X and Y). The resources need to
produce X and Y are twofold, namely machine
time for automatic processing and craftsman
time for hand finishing. The table below gives
the number of minutes required for each item:
Machine time Craftsman time
Item X 13 20
Y 19 29

51. The company has 40 hours of machine time
available in the next working week but only 35
hours of craftsman time. Machine time is costed
at £10 per hour worked and craftsman time is
costed at £2 per hour worked. Both machine
and craftsman idle times incur no costs. The
revenue received for each item produced (all
production is sold) is £20 for X and £30 for Y. The
company has a specific contract to produce 10
items of X per week for a particular customer

52. • Formulate the problem of deciding how much
to produce per week as a linear program.
• Solve this linear program graphically.
Let
• x be the number of items of X
• y be the number of items of Y

53. then the LP is:
maximise
• 20x + 30y - 10(machine time worked) -
2(craftsman time worked)
subject to:
• 13x + 19y <= 40(60) machine time
• 20x + 29y <= 35(60) craftsman time
• x >= 10 contract
• x,y >= 0
• so that the objective function becomes

54. maximise
• 20x + 30y - 10(13x + 19y)/60 - 2(20x + 29y)/60
i.e. maximise
• 17.1667x + 25.8667y
subject to:
• 13x + 19y <= 2400
• 20x + 29y <= 2100
• x >= 10
• x,y >= 0

55. It is plain from the diagram below that the
maximum occurs at the intersection of x=10 and
20x + 29y <= 2100
Solving simultaneously, rather than by reading
values off the graph, we have that x=10 and
y=65.52 with the value of the objective function
being £1866.5

57. Excercises
1. A company manufactures two products (A
and B) and the profit per unit sold is £3 and £5
respectively. Each product has to be assembled
on a particular machine, each unit of product A
taking 12 minutes of assembly time and each
unit of product B 25 minutes of assembly time.
The company estimates that the machine used
for assembly has an effective working week of
only 30 hours (due to maintenance/breakdown).

58. • Technological constraints mean that for every five
units of product A produced at least two units of
product B must be produced.
• Formulate the problem of how much of each
product to produce as a linear program.
• Solve this linear program graphically.
• The company has been offered the chance to hire
an extra machine, thereby doubling the effective
assembly time available. What is
the maximum amount you would be prepared to
pay (per week) for the hire of this machine and
why?

59. • 2. Solve the following linear program:
• maximise 5x1 + 6x2
• subject to
• x1 + x2 <= 10
• x1 - x2 >= 3
• 5x1 + 4x2 <= 35
• x1 >= 0
• x2 >= 0

60. • 3. Solve
• minimise
• 4a + 5b + 6c
• subject to
• a + b >= 11
• a - b <= 5
• c - a - b = 0
• 7a >= 35 - 12b
• a >= 0 b >= 0 c >= 0

61. • 4.A carpenter makes tables and chairs. Each table
can be sold for a profit of £30 and each chair for a
profit of £10. The carpenter can afford to spend
up to 40 hours per week working and takes six
hours to make a table and three hours to make a
chair. Customer demand requires that he makes
at least three times as many chairs as tables.
Tables take up four times as much storage space
as chairs and there is room for at most four tables
each week.
Formulate this problem as a linear programming
problem and solve it graphically.

62. • 5. A farmer can plant up to 8 acres of land with
wheat and barley. He can earn $5,000 for every
acre he plants with wheat and $3,000 for every
acre he plants with barley. His use of a
necessary pesticide is limited by federal
regulations to 10 gallons for his entire 8 acres.
Wheat requires 2 gallons of pesticide for every
acre planted and barley requires just 1 gallon
per acre.
What is the maximum profit he can make?

63. • 6. A painter has exactly 32 units of yellow dye and
54 units of green dye.
He plans to mix as many gallons as possible of
color A and color B.
Each gallon of color A requires 4 units of yellow
dye and 1 unit of green dye.
Each gallon of color B requires 1 unit of yellow
dye and 6 units of green dye.
Find the maximum number of gallons he can
mix.

64. • 7. The Bead Store sells material for customers to
make their own jewelry. Customer can select
beads from various bins. Grace wants to design
her own Halloween necklace from orange and
black beads. She wants to make a necklace that is
at least 12 inches long, but no more than 24
inches long. Grace also wants her necklace to
contain black beads that are at least twice the
length of orange beads. Finally, she wants her
necklace to have at least 5 inches of black beads.
Find the constraints, sketch the problem and find
the vertices (intersection points)

65. 8.A garden shop wishes to prepare a supply
of special fertilizer at a minimal cost by
mixing two fertilizers, A and B.

66. • The mixture is to contain:
at least 45 units of phosphate
at least 36 units of nitrate
at least 40 units of ammonium
Fertilizer A costs the shop $.97 per pound.
Fertilizer B costs the shop $1.89 per pound.
fertilizer A contains 5 units of phosphate and 2
units of nitrate and 2 units of ammonium.
fertilizer B contains 3 units of phosphate and 3
units of nitrate and 5 units of ammonium.
how many pounds of each fertilizer should the
shop use in order to minimize their cost.