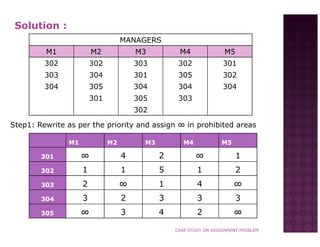
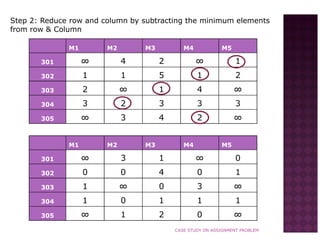
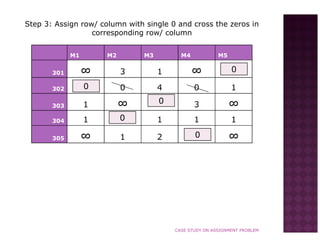
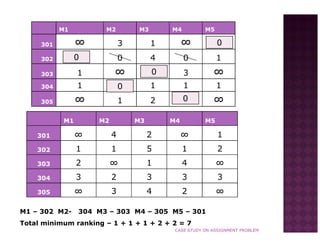
Managers were asked to rank their preferences for 5 rooms (301, 302, 303, 304, 305). Using the Hungarian method, the rooms were assigned to minimize total preference ranking. The method involved subtracting minimums, assigning singles, crossing zeros, and iterating until all rows/columns had a zero. The optimal assignment was: M1 to room 302, M2 to room 304, M3 to room 303, M4 to room 305, and M5 to room 301. This yielded a minimum total ranking of 7.

1. Prepared By:
HARSH VYAS - 212011
RESHMI RAVEENDRAN - 1
212027
CASE STUDY ON ASSIGNMENT PROBLEM

2. Well-Done Company has taken the third floor of a building for rent with a view to locate one of
their zonal offices. There are five main rooms in this to be assigned to five managers. Each room
has its own advantages and disadvantages.
Some have windows, some are closer to the washroom or to the canteen or secretarial pool. The
rooms are of all different sizes and shapes. Each of the five managers were asked to rank their
room preferences amongst the rooms 301, 302, 303, 304 and 305. Their preferences were
recorded in a table as indicated below:
MANAGERS
M1
M2
M3
M4
M5
302
302
303
302
301
303
304
301
305
302
304
305
304
304
304
301
305
303
302
Most of the managers did not list all the five rooms since they were not satisfied with some of
these rooms and they have left these from the list. Assuming that their preferences can be
quantified by numbers, find out as to which manager should be assigned to which room so that
their total preference ranking is a minimum.
CASE STUDY ON ASSIGNMENT PROBLEM

3. Maximization Or Minimization Problem
Check whether the problem is Balanced
If there are any prohibit assignments, then assign ‘∞’
Proceed with Hungarian Method : Subtract the Minimum from each row
Subtract the minimum from each column
Find the row with single zero & assign that zero
Find the column with single zero & assign
Cancel all zero in the corresponding row & coloumn of the assigned
zero
Draw Minimum no. of Lines to cover all zeros
Select the minimum (lets say Ө) uncrossed element and subtract it
from rest uncrossed elements. In case of row/coloumn elements
crossed by lines write the elements as it is & in case of elements
intersected by 2 lines add Ө
Proceed with the new matrix as in step 4 until all rows and coloums
have a ‘0’ assigned to the corresponding parameters.
CASE STUDY ON ASSIGNMENT PROBLEM

4. Solution :
MANAGERS
M1
M2
M3
M4
M5
302
302
303
302
301
303
304
301
305
302
304
305
304
304
304
301
305
303
302
Step1: Rewrite as per the priority and assign ∞ in prohibited areas
M1
M2
M3
M4
M5
301
∞
4
2
∞
1
302
1
1
5
1
2
303
2
∞
1
4
∞
304
3
2
3
3
3
305
∞
3
4
2
∞
CASE STUDY ON ASSIGNMENT PROBLEM

5. Step 2: Reduce row and column by subtracting the minimum elements
from row & Column
M1
M2
M3
M4
M5
301
∞
4
2
∞
1
302
1
1
5
1
2
303
2
∞
1
4
∞
304
3
2
3
3
3
305
∞
3
4
2
∞
M1
M2
M3
M4
M5
301
∞
3
1
∞
0
302
0
0
4
0
1
303
1
∞
0
3
∞
304
1
0
1
1
1
305
∞
1
2
0
∞
CASE STUDY ON ASSIGNMENT PROBLEM

6. Step 3: Assign row/ column with single 0 and cross the zeros in
corresponding row/ column
M1
M2
M3
M4
M5
301
∞
3
1
∞
0
302
0
0
4
0
1
303
1
∞
0
3
∞
304
1
0
1
1
1
305
∞
1
2
0
∞
6
CASE STUDY ON ASSIGNMENT PROBLEM

7. M1
M2
M3
M4
M5
301
∞
3
1
∞
0
302
0
0
4
0
1
303
1
∞
0
3
∞
304
1
0
1
1
1
305
∞
1
2
0
∞
M1
M2
M3
M4
M5
301
∞
4
2
∞
1
302
1
1
5
1
2
303
2
∞
1
4
∞
304
3
2
3
3
3
305
∞
3
4
2
∞
M1 – 302 M27
304 M3 – 303 M4 – 305 M5 – 301
Total minimum ranking – 1 + 1 + 1 + 2 + 2 = 7
CASE STUDY ON ASSIGNMENT PROBLEM

8. Thank you