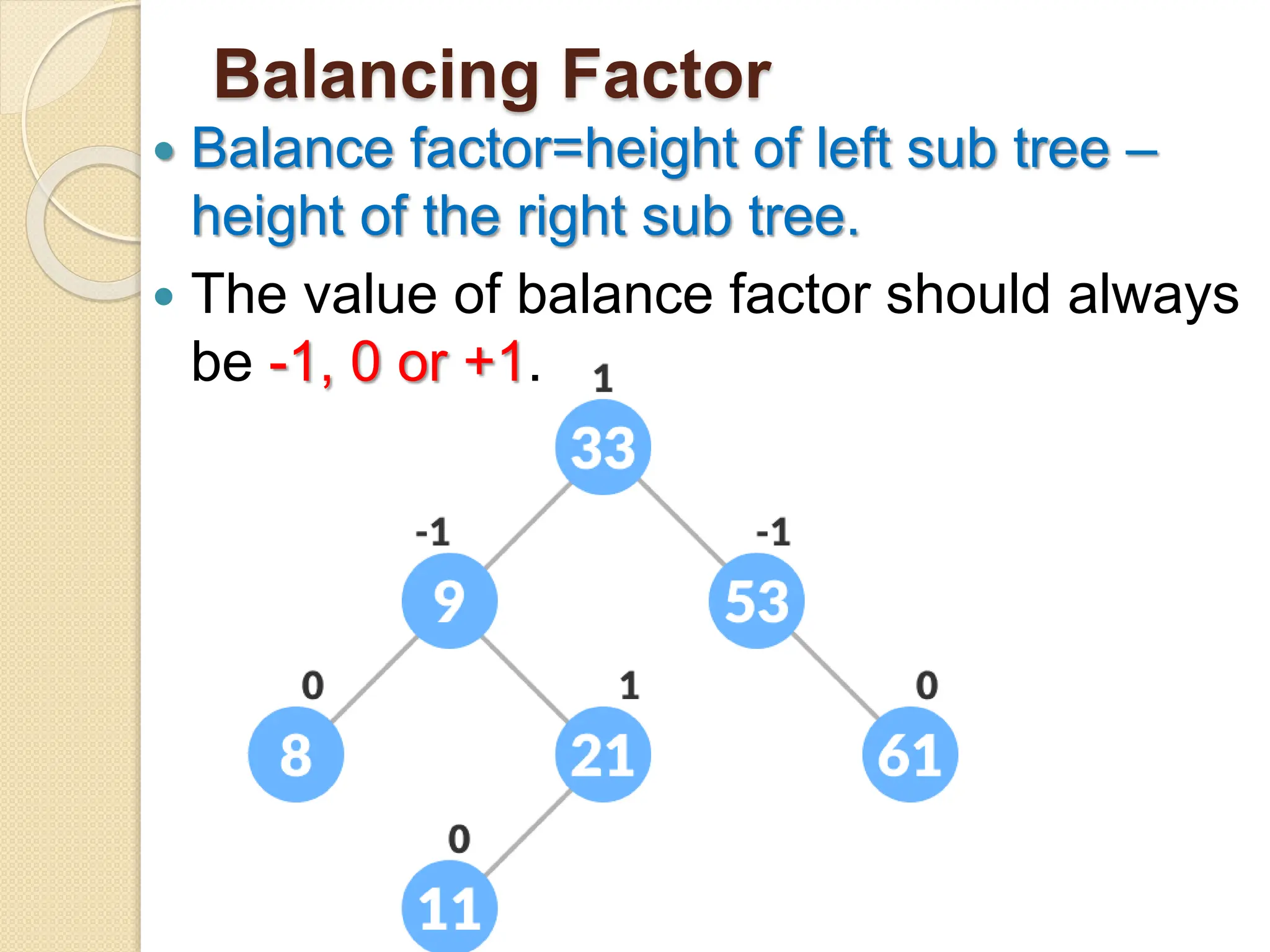
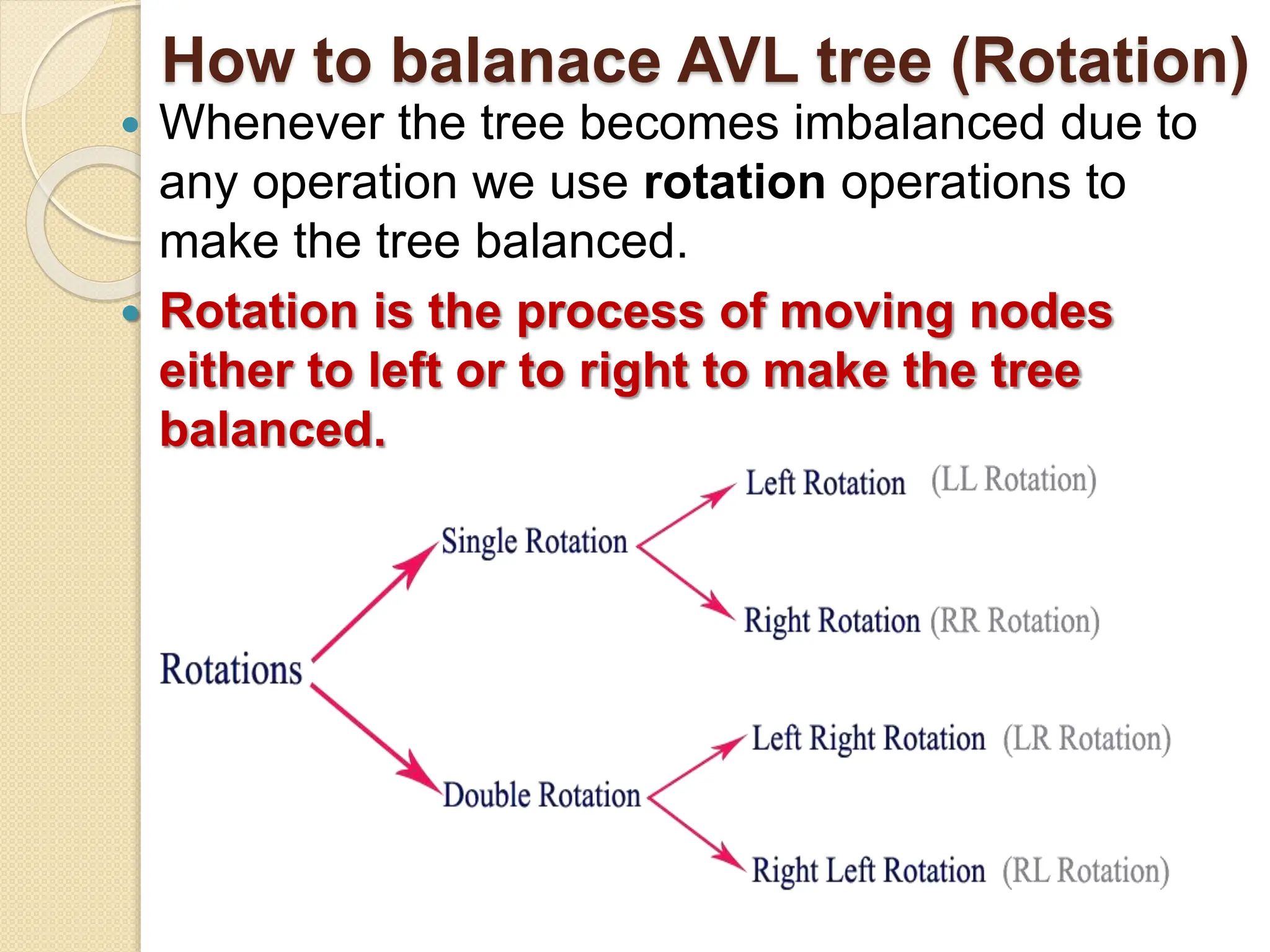
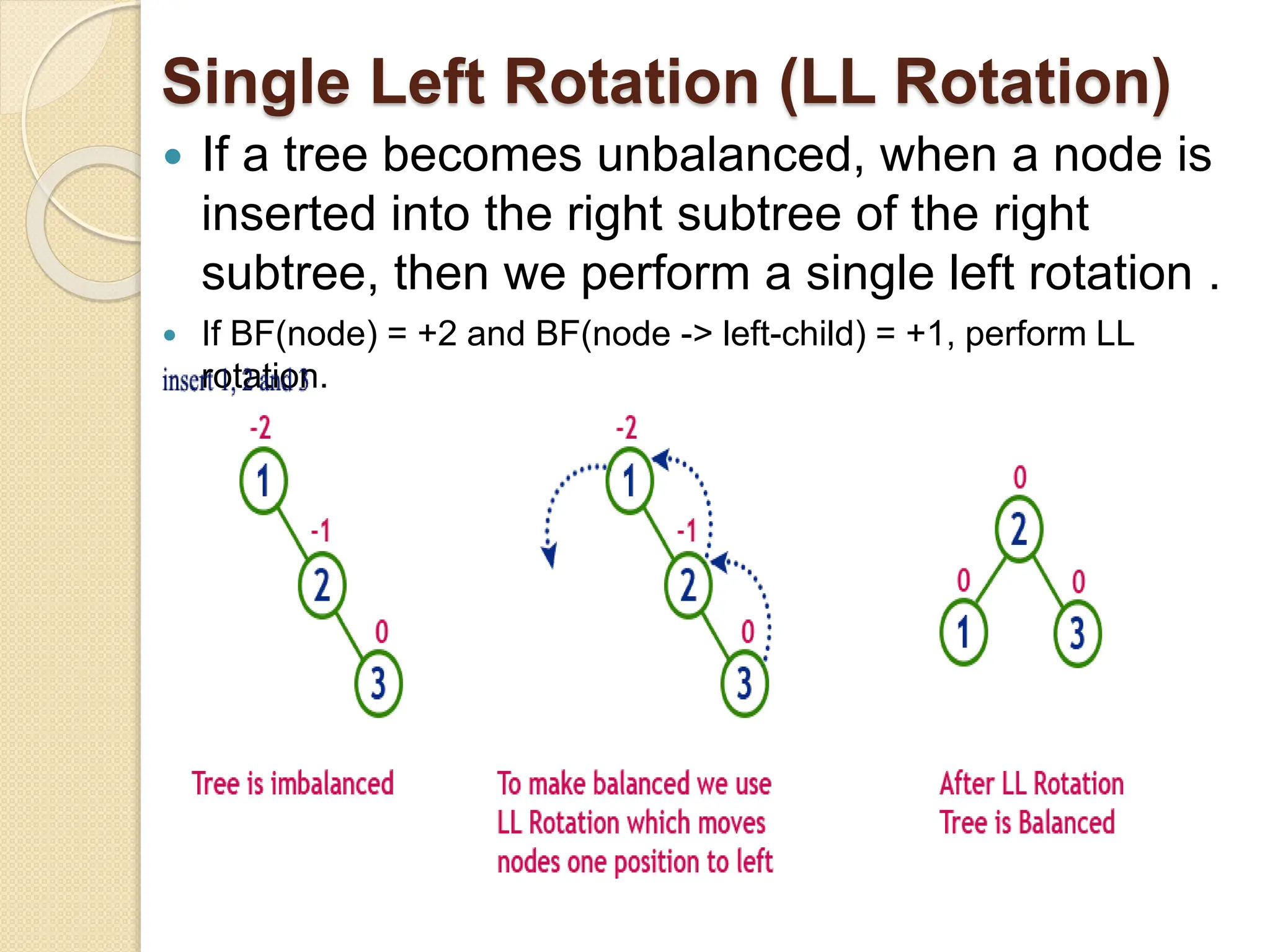
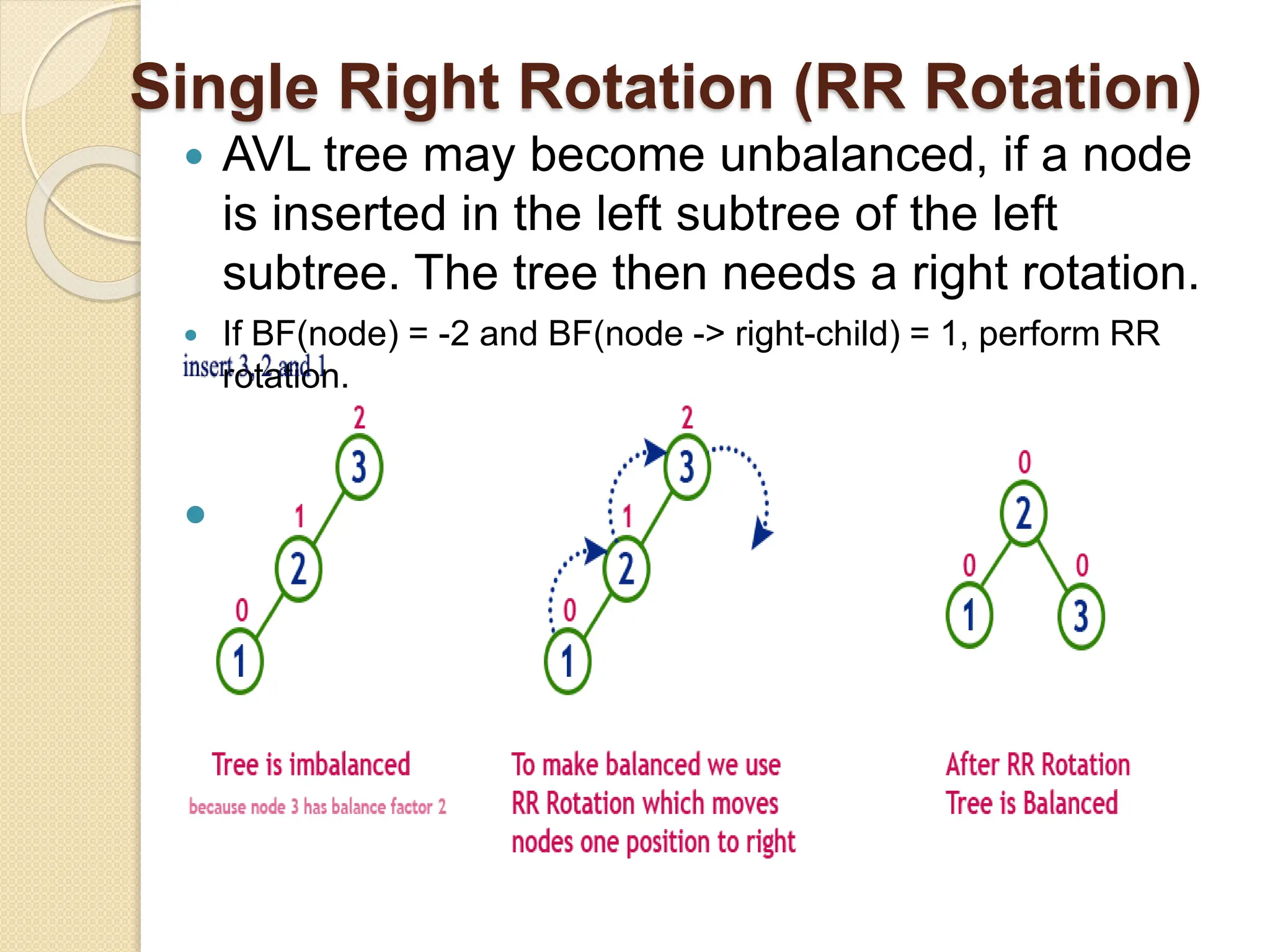
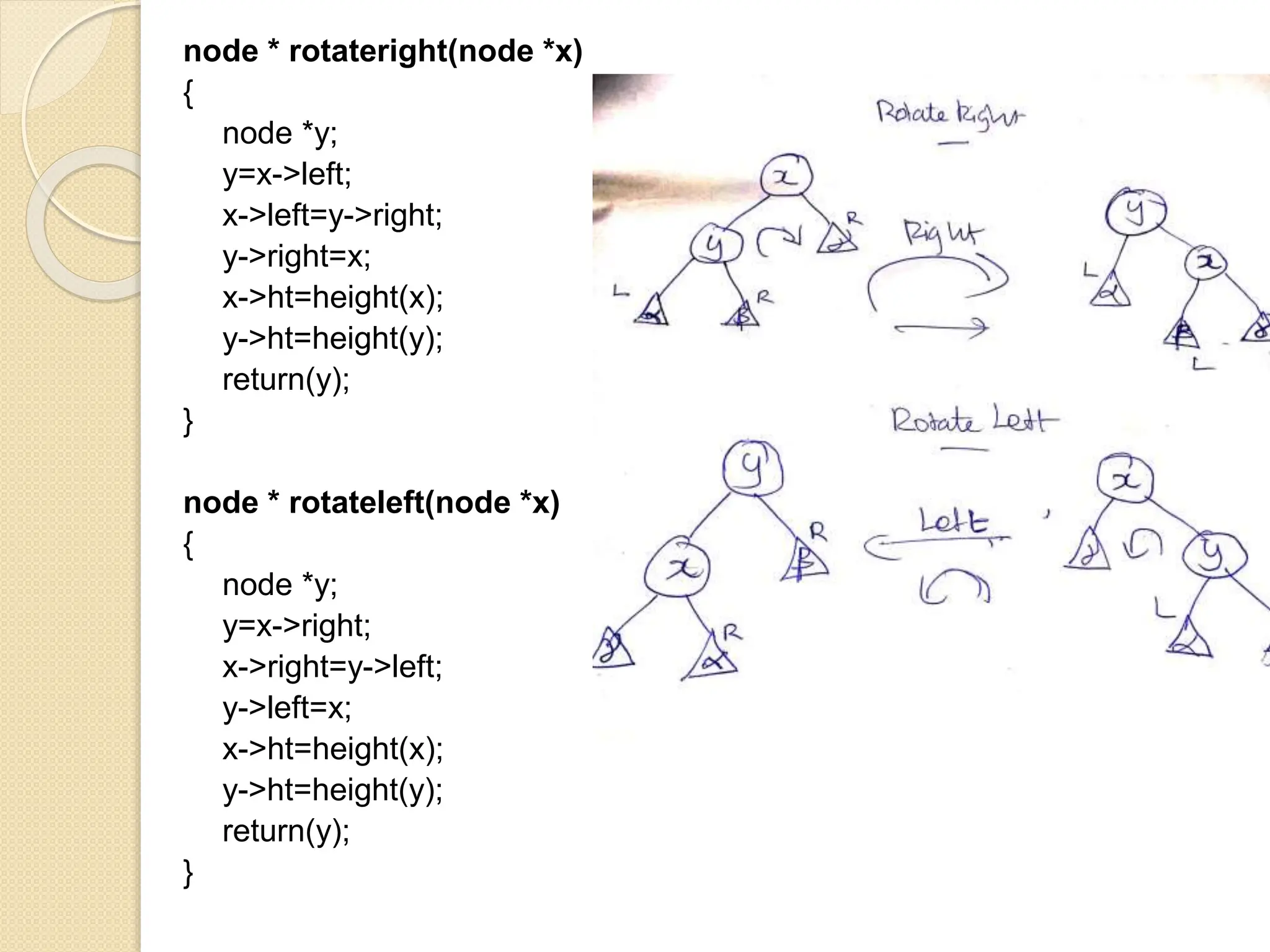
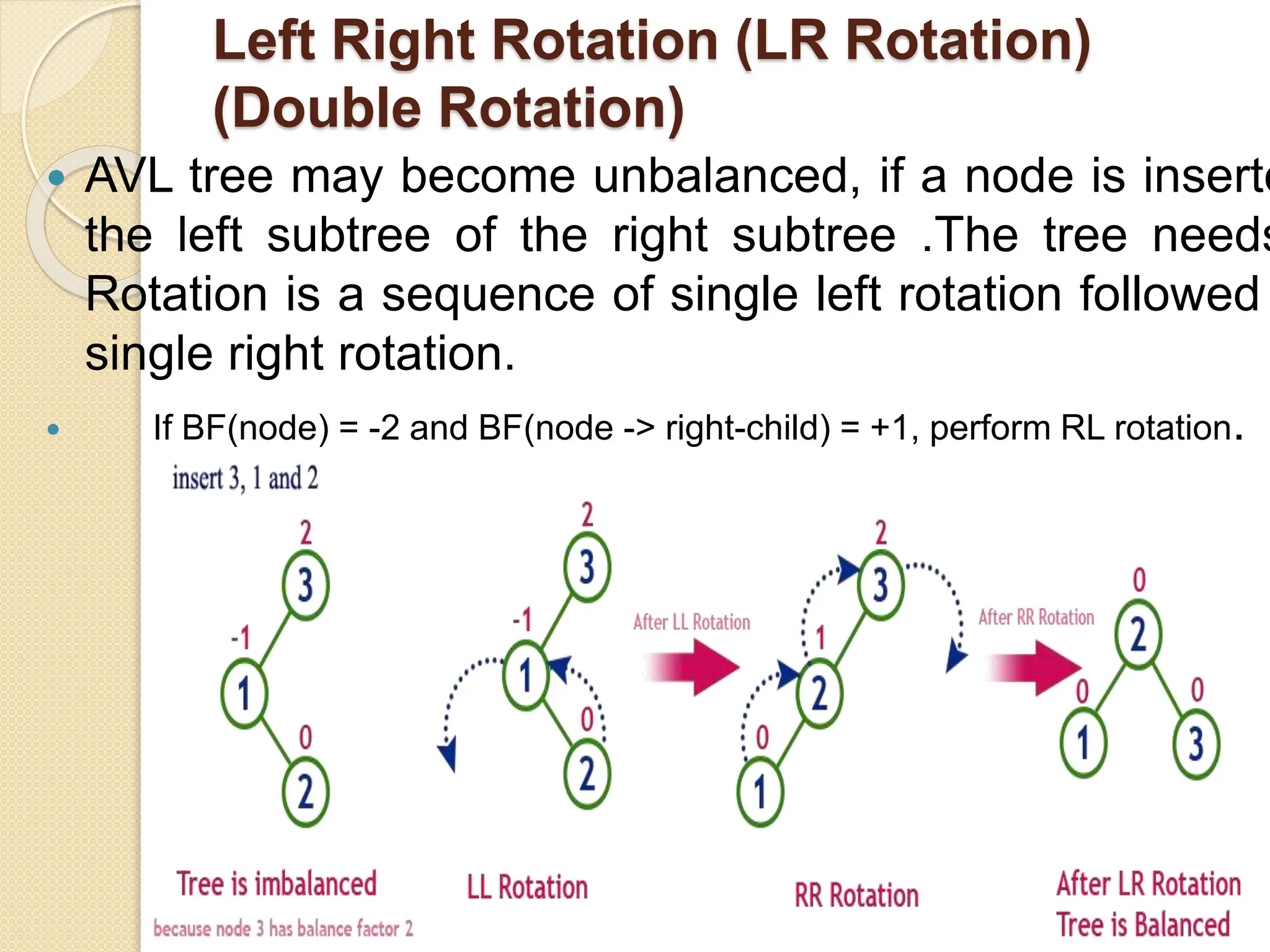
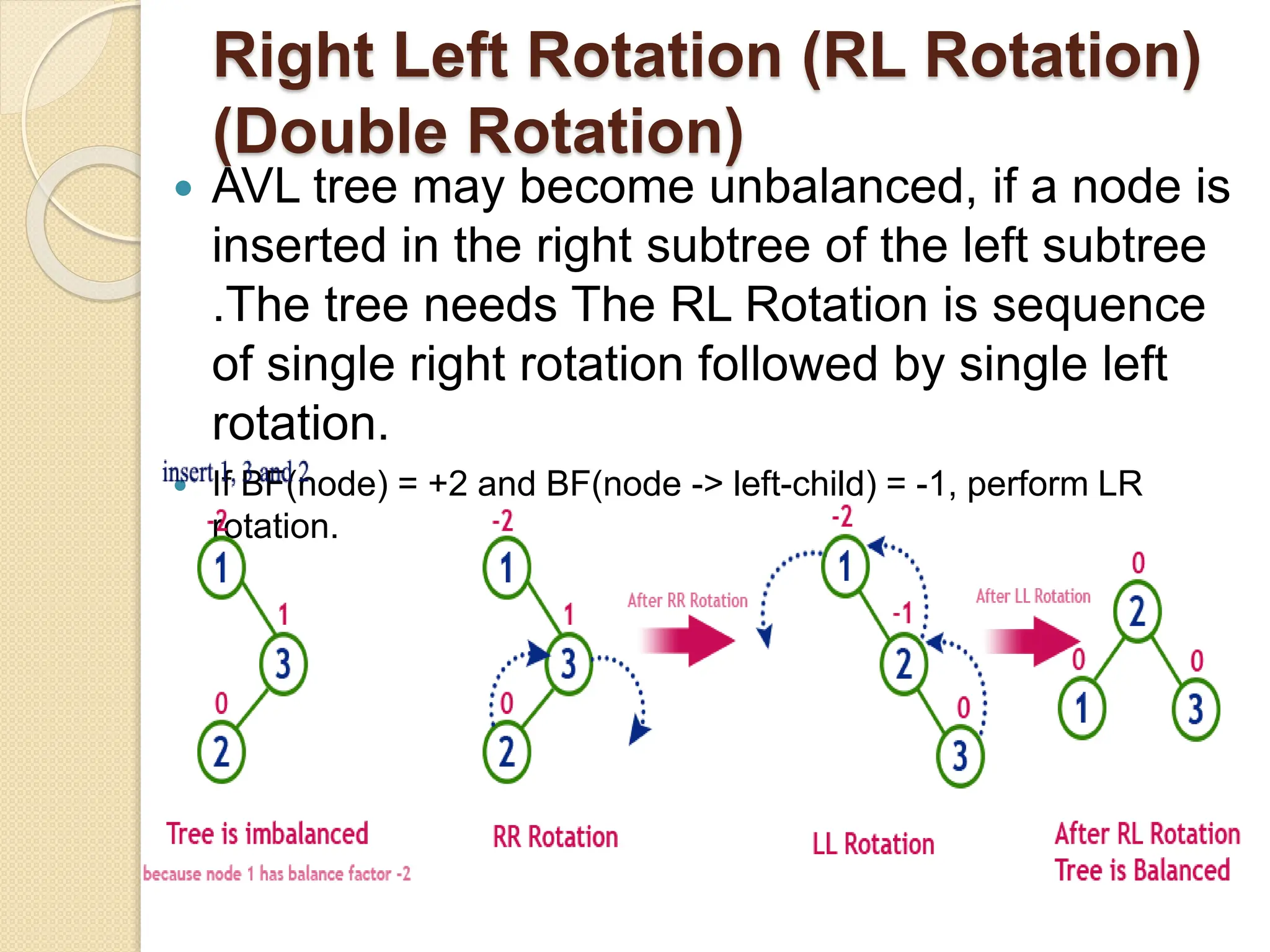
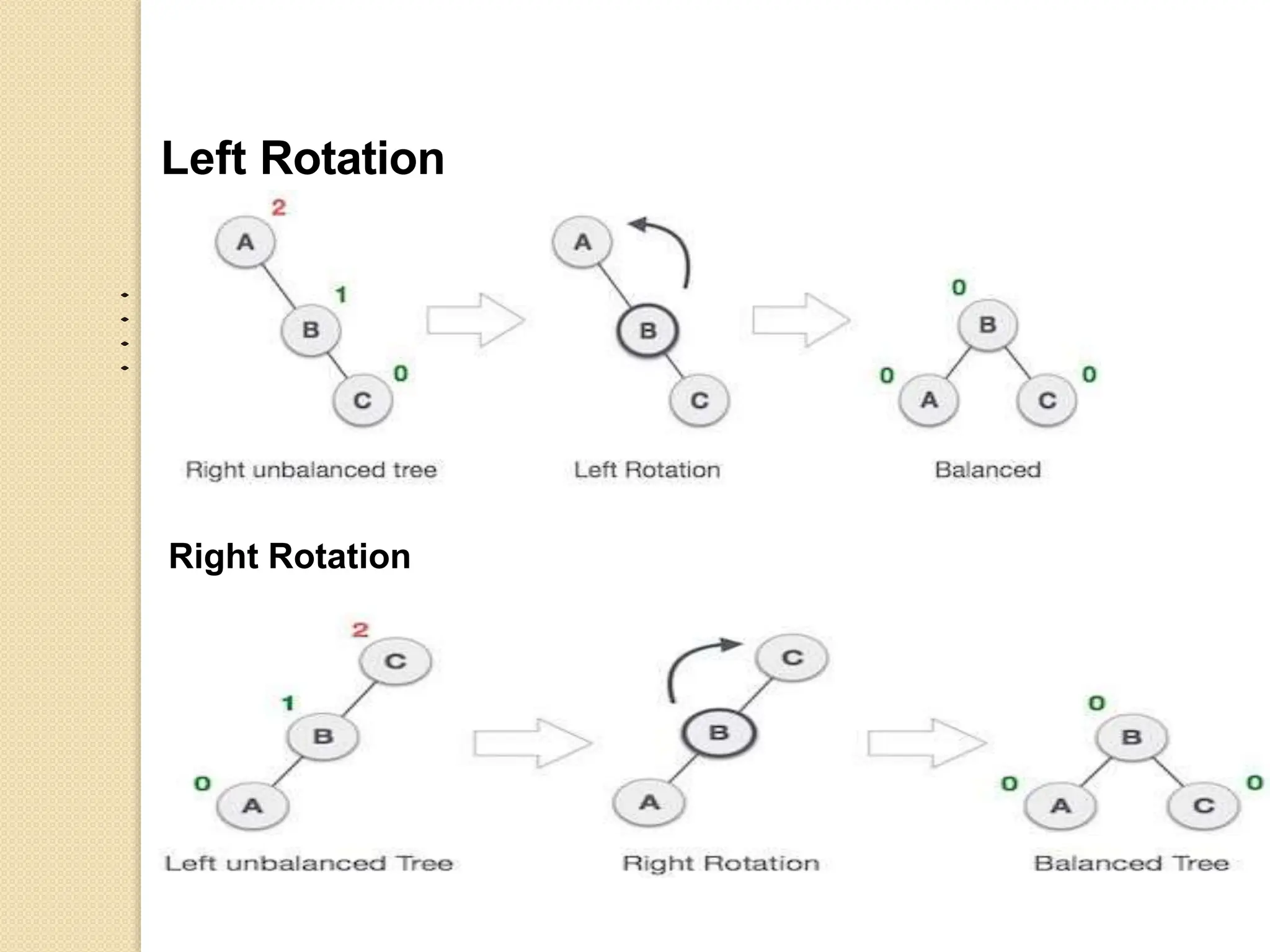
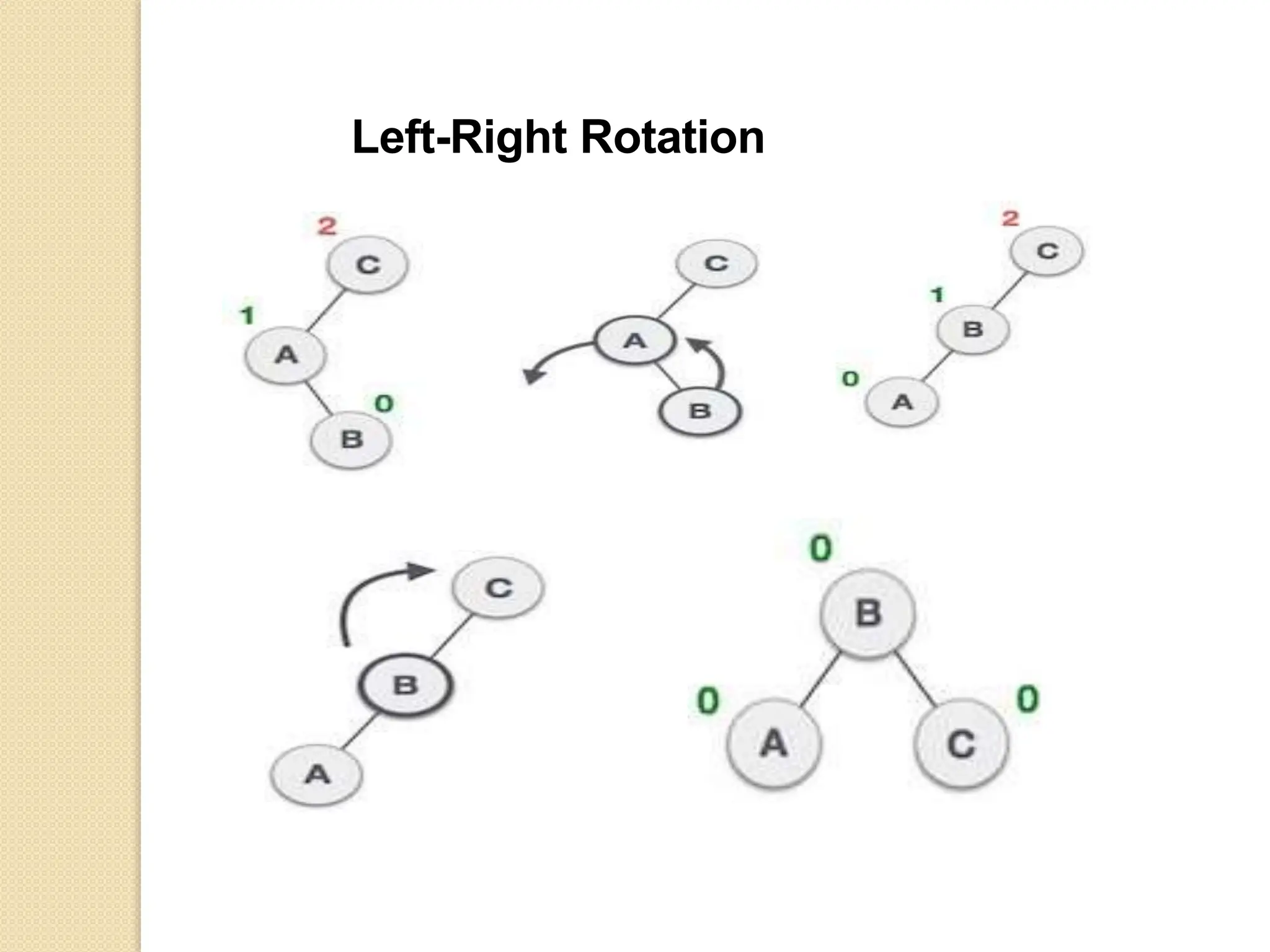
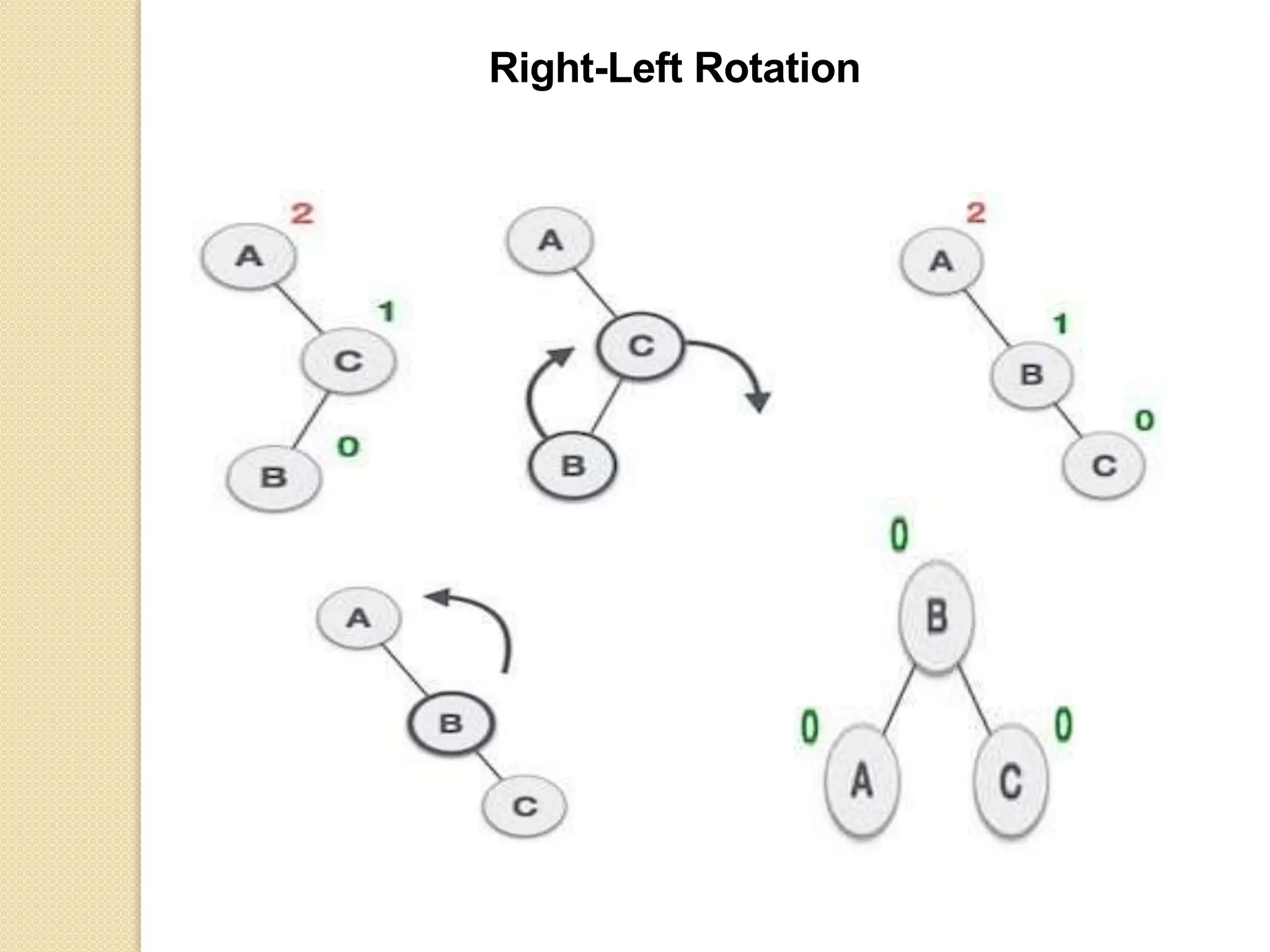
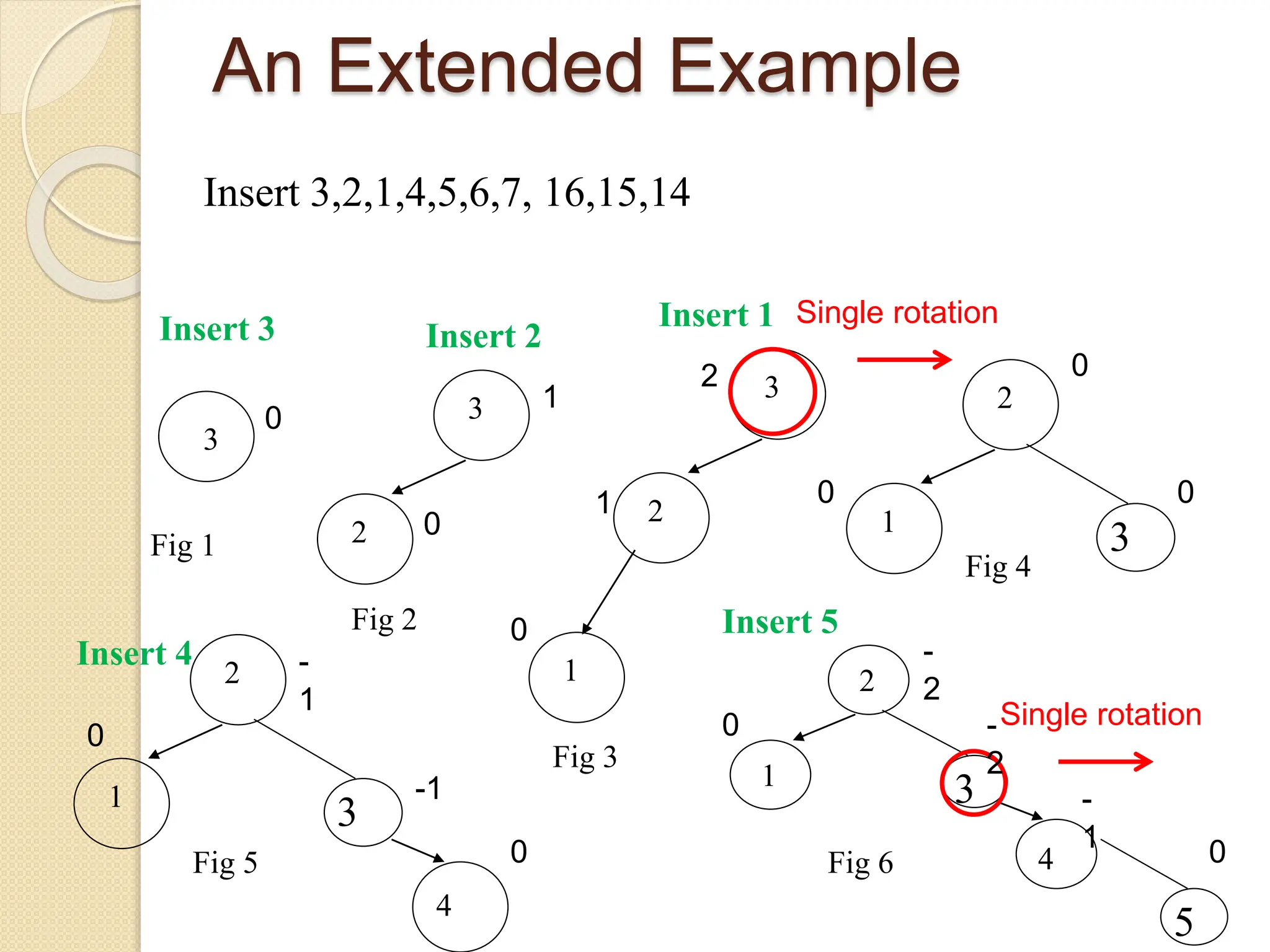
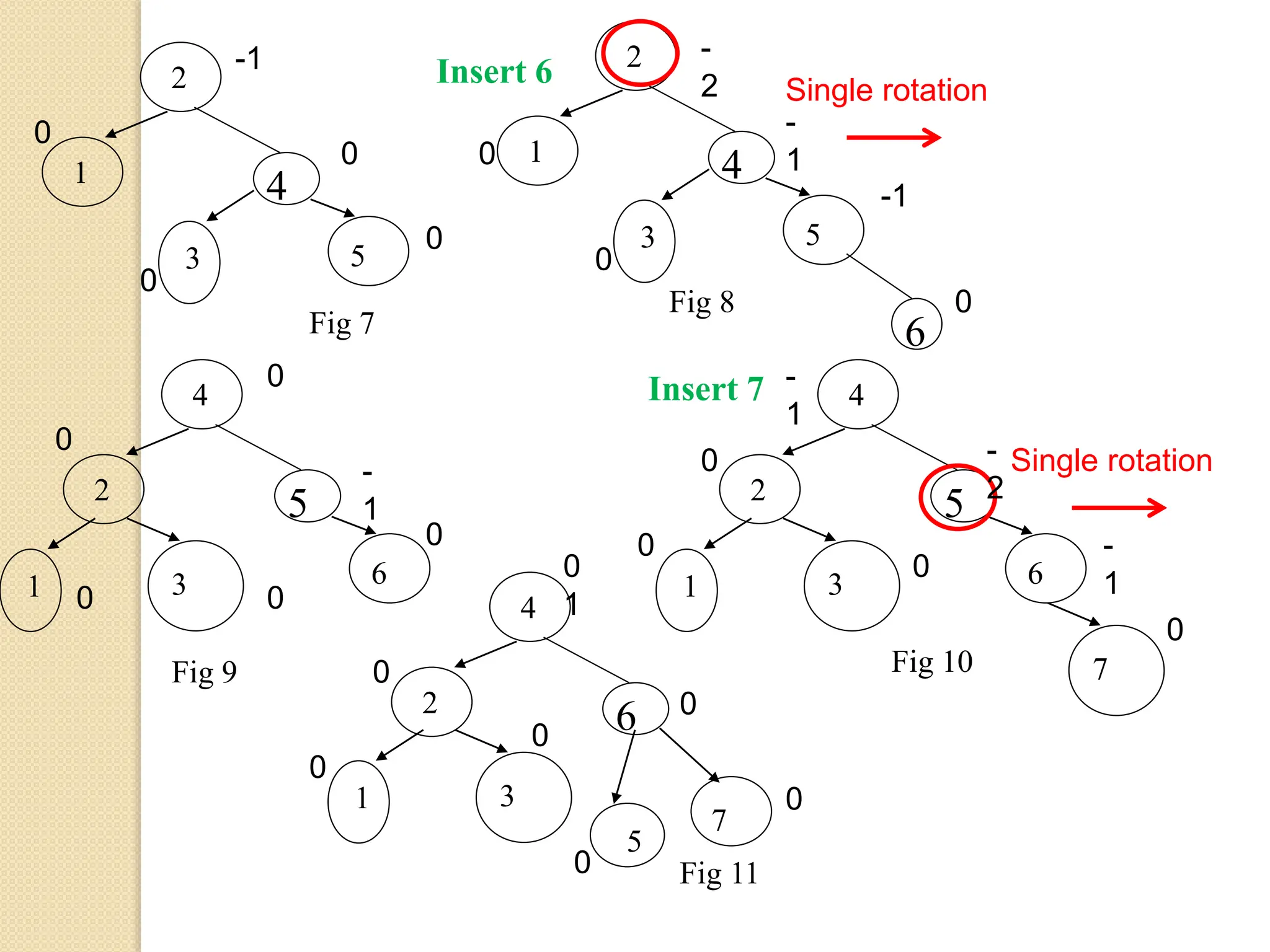
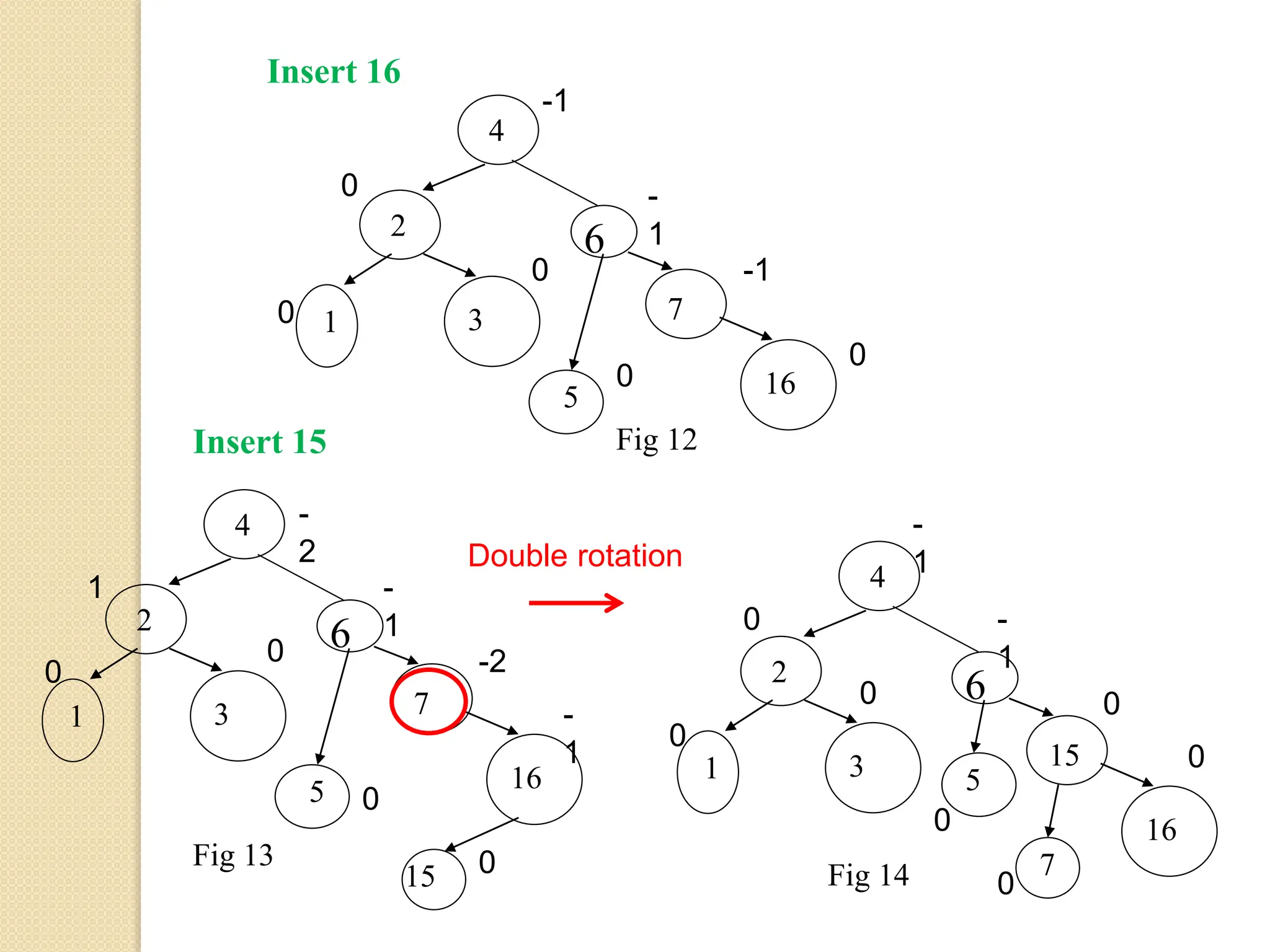
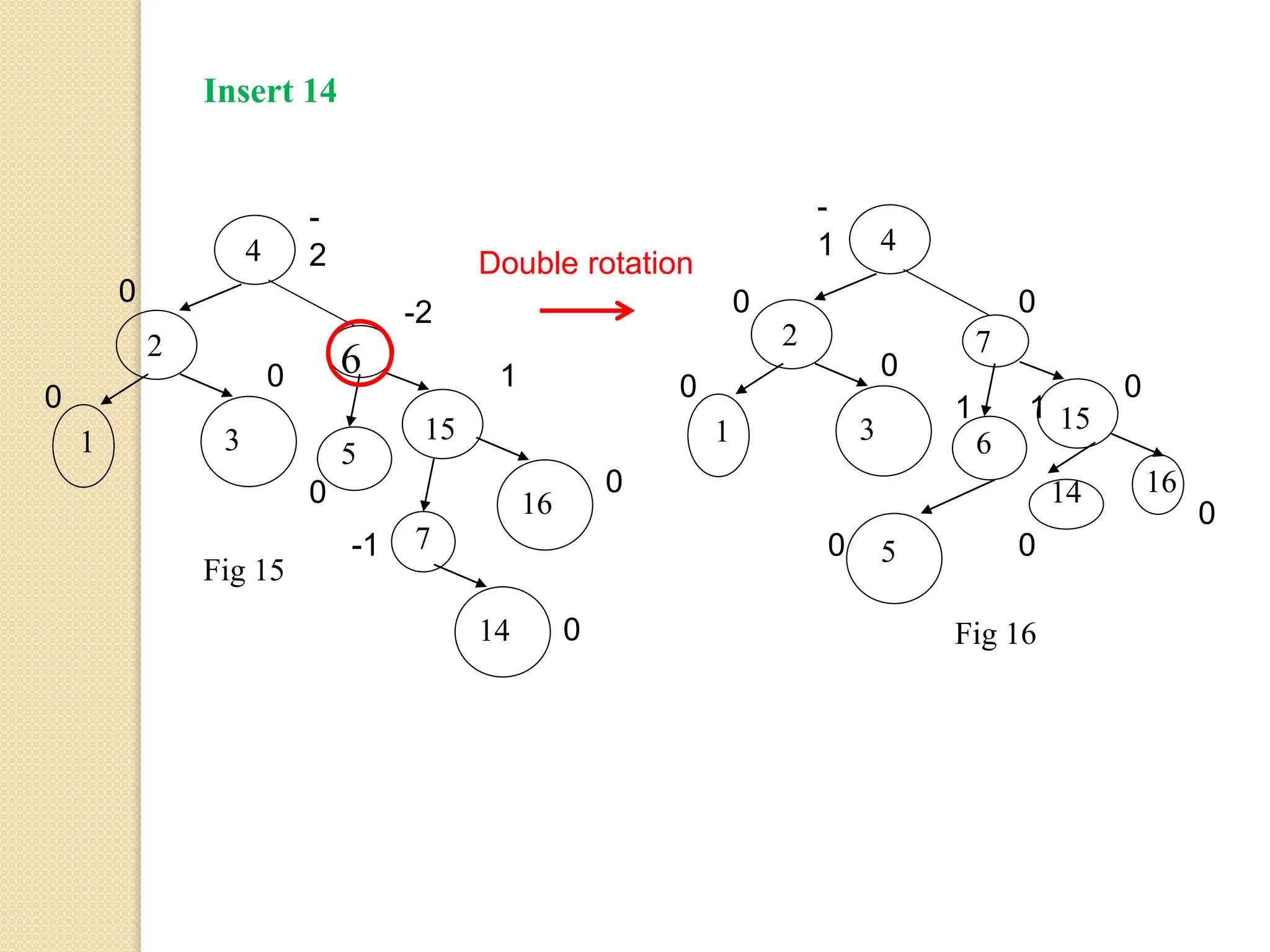
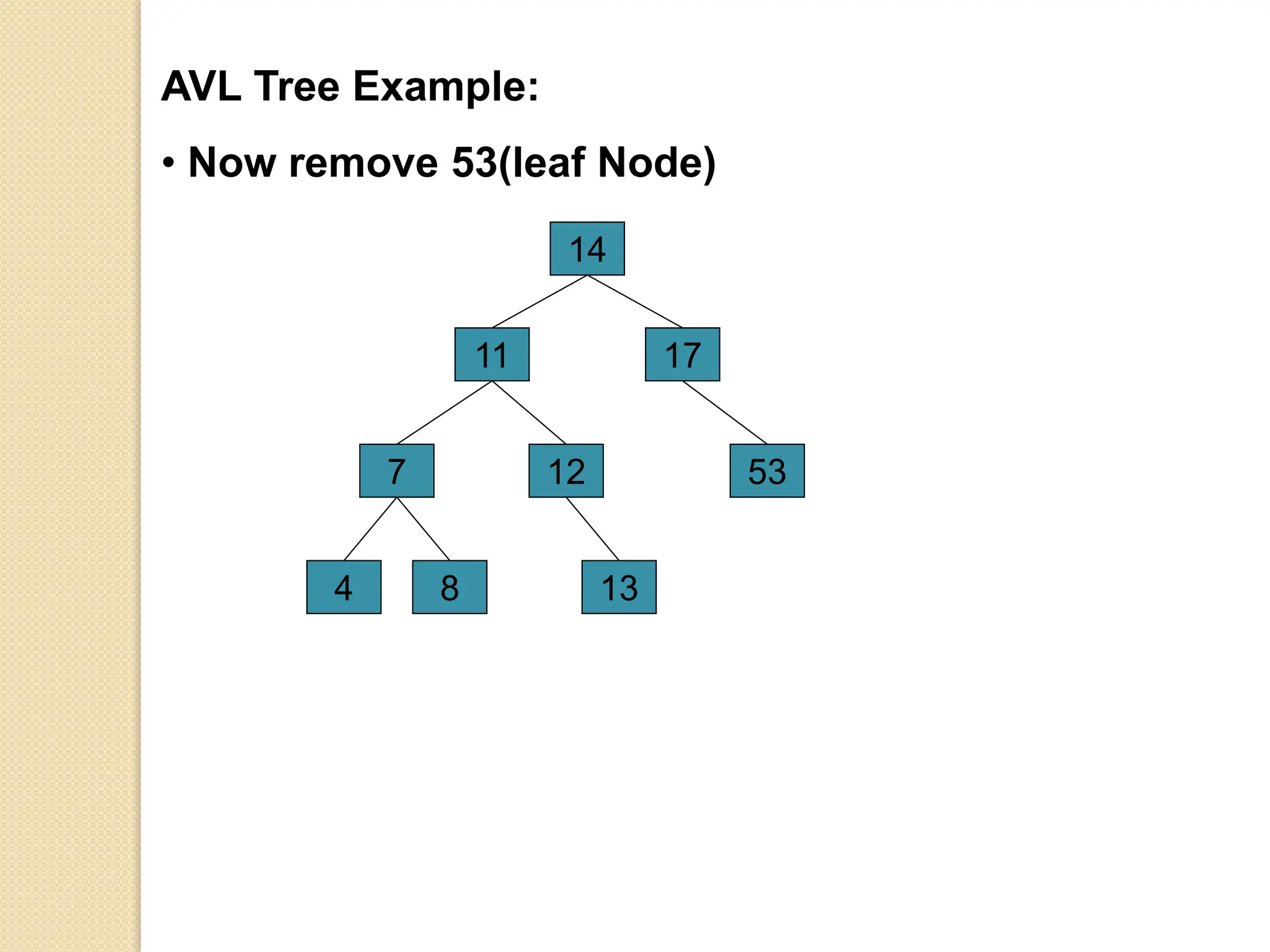
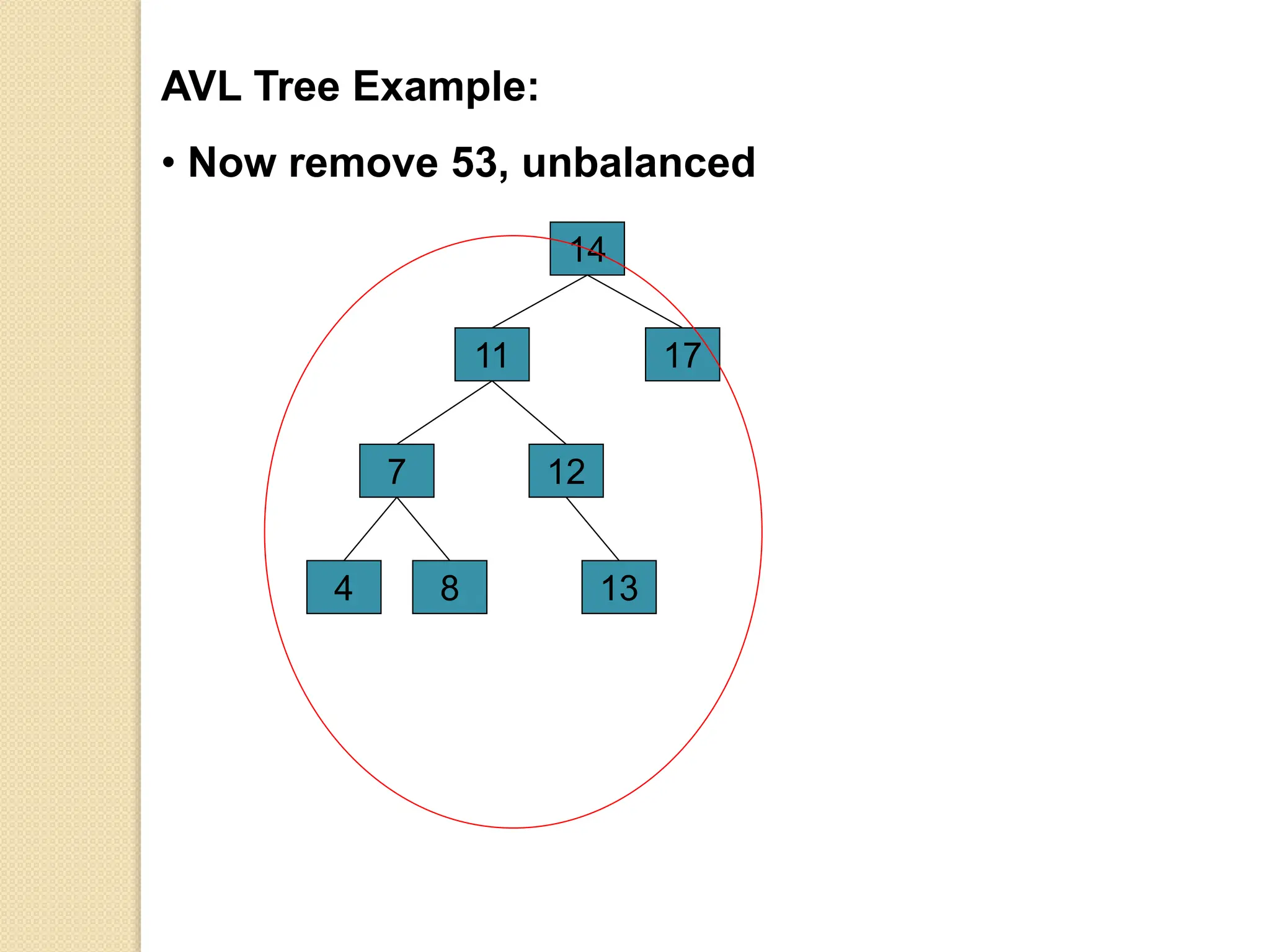
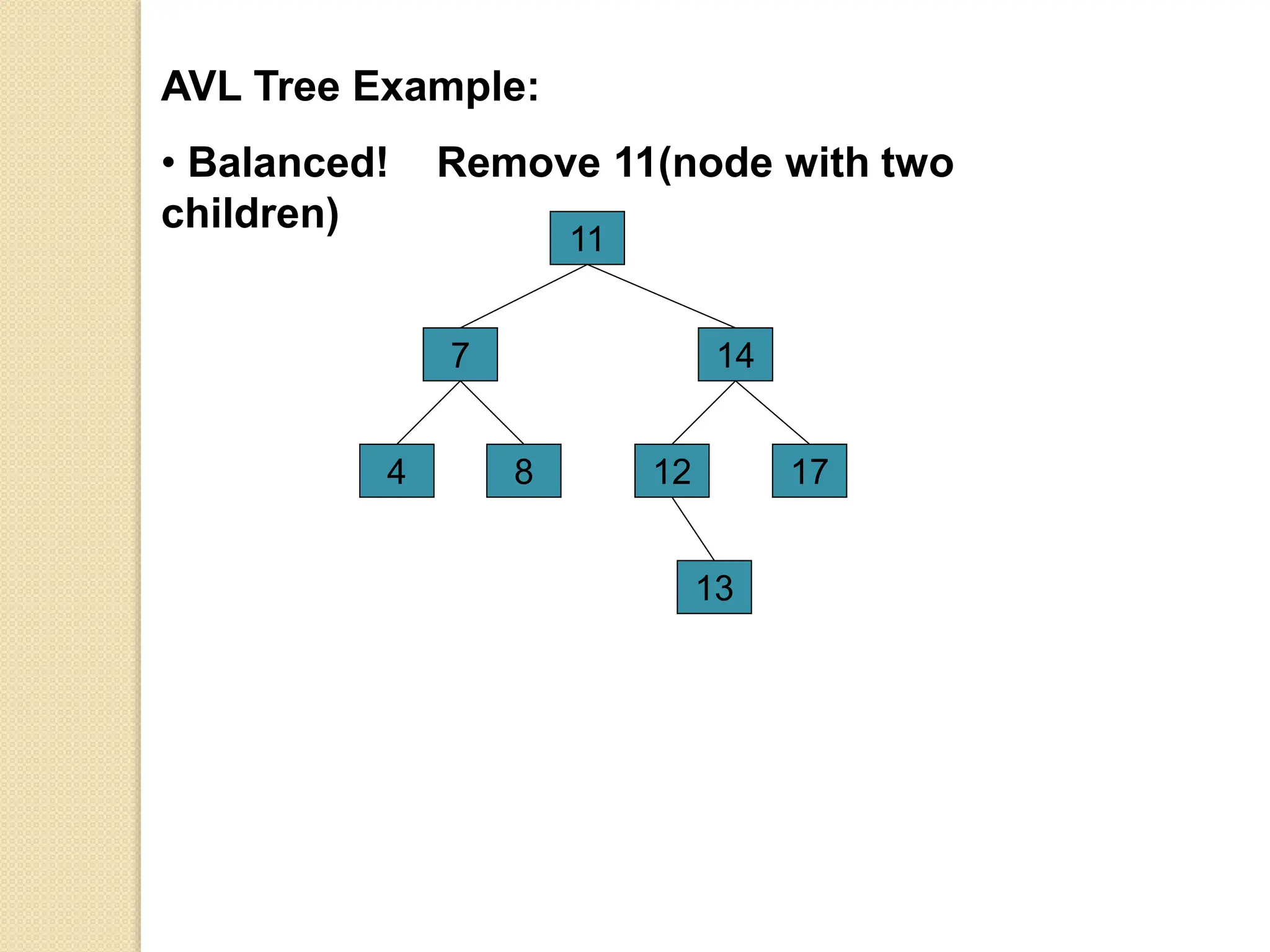
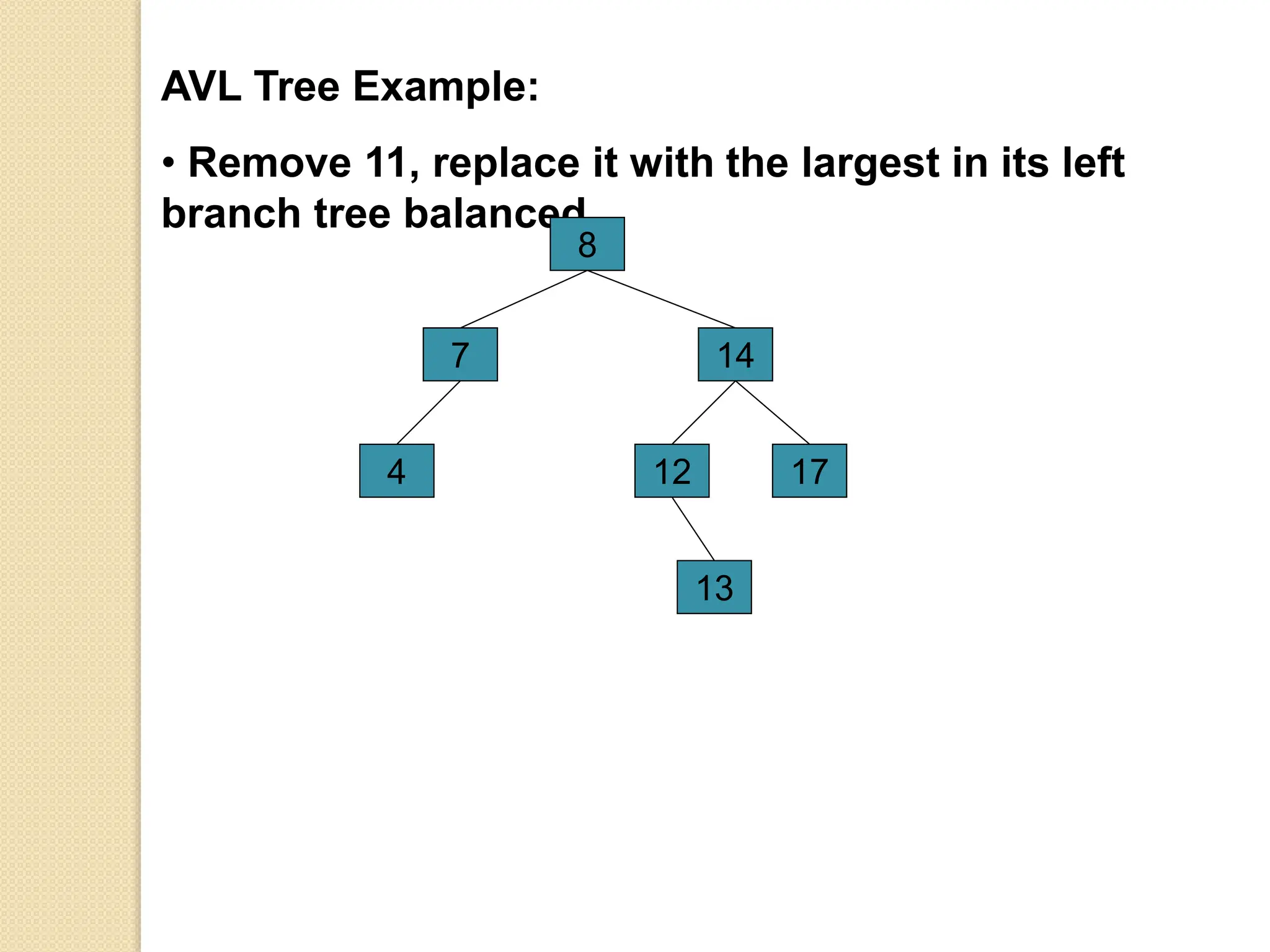
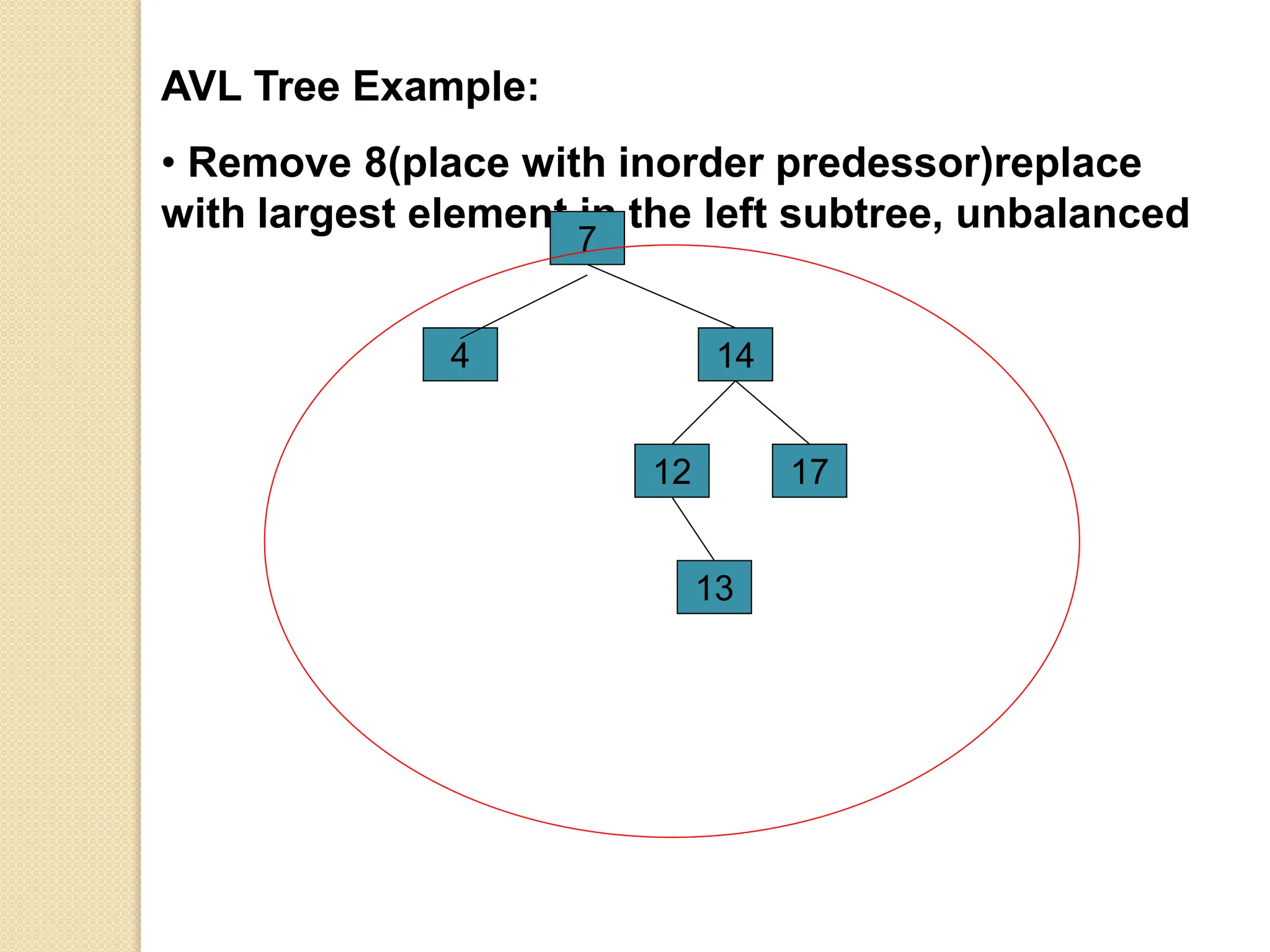
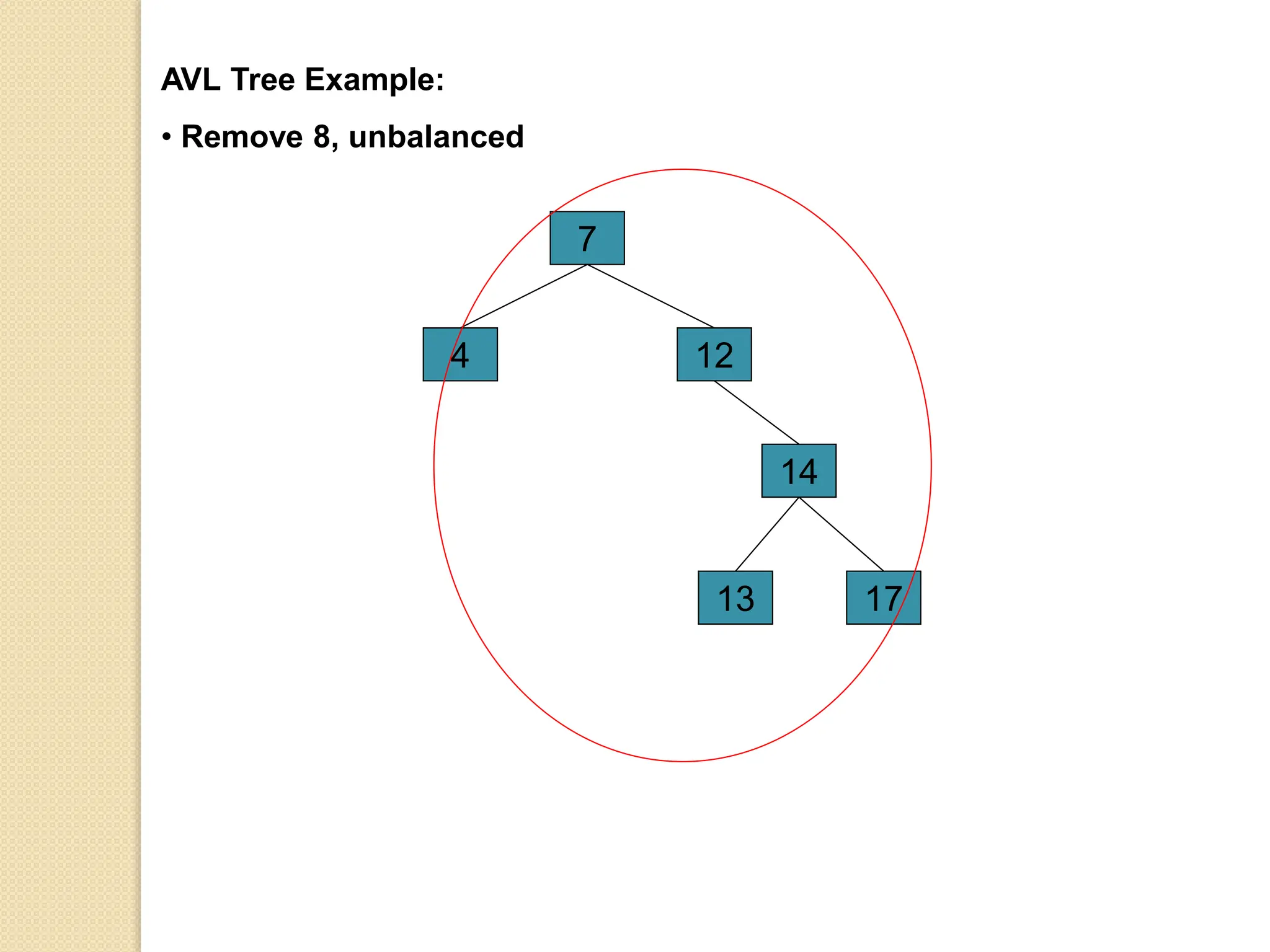
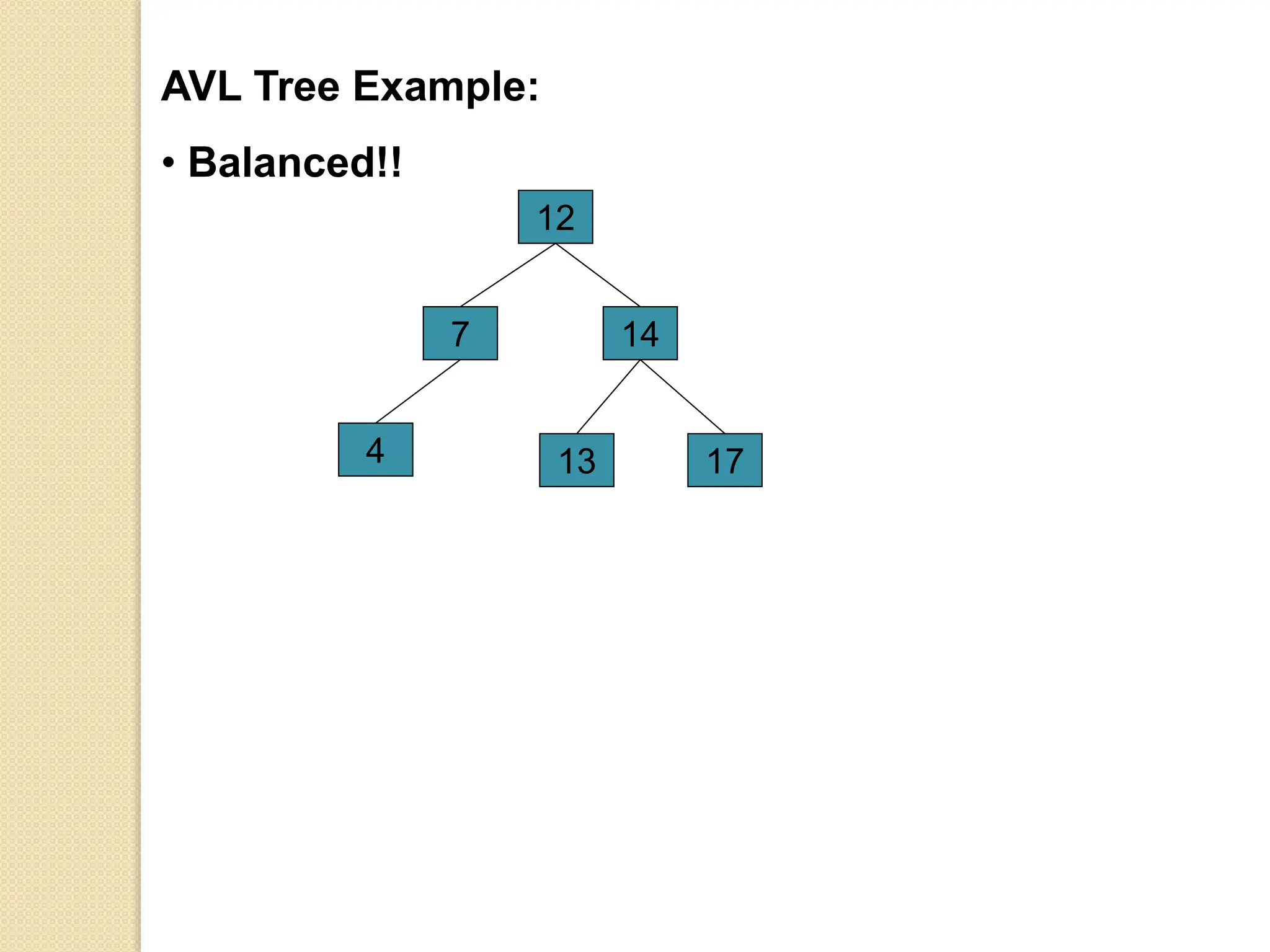
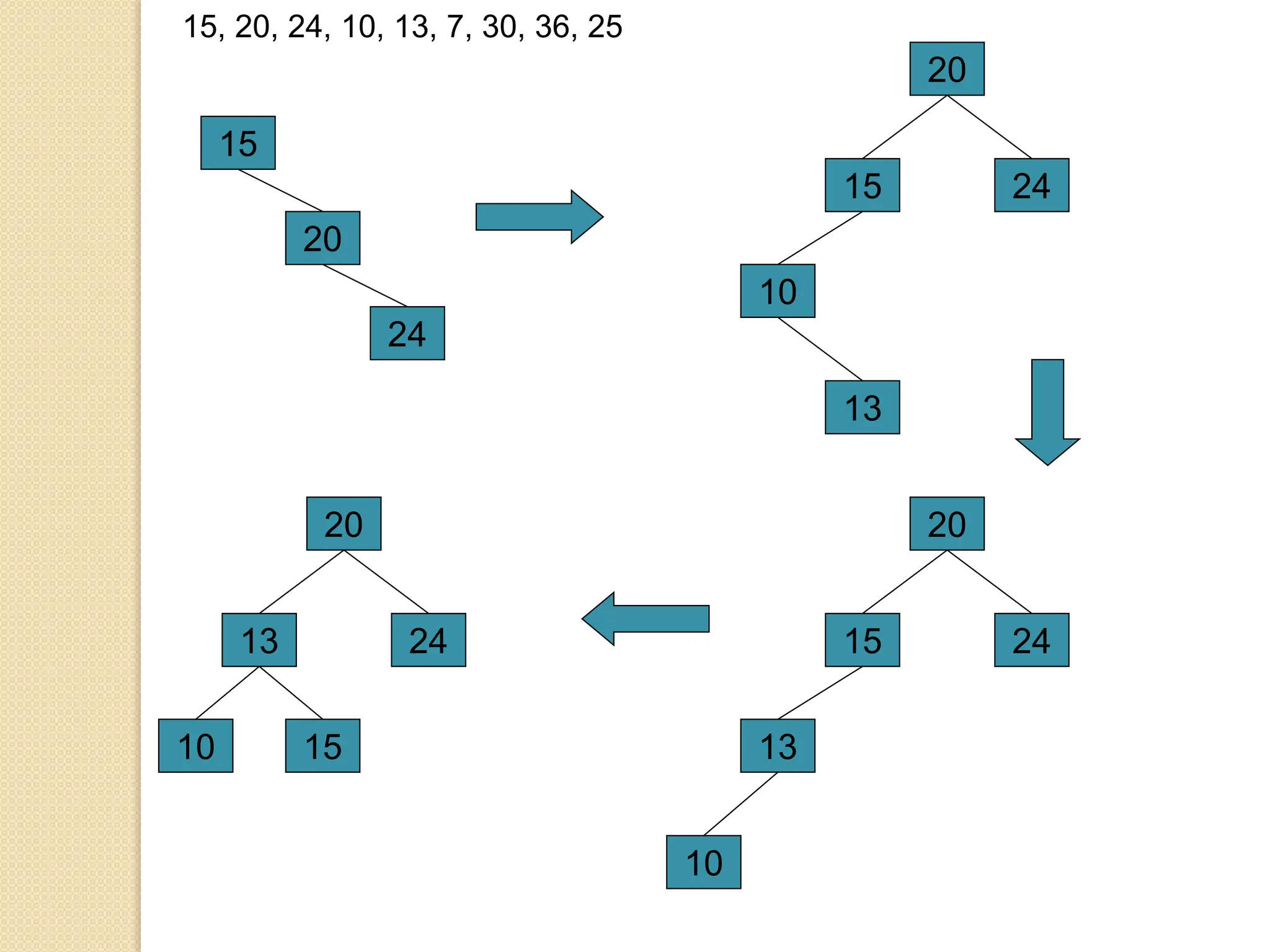
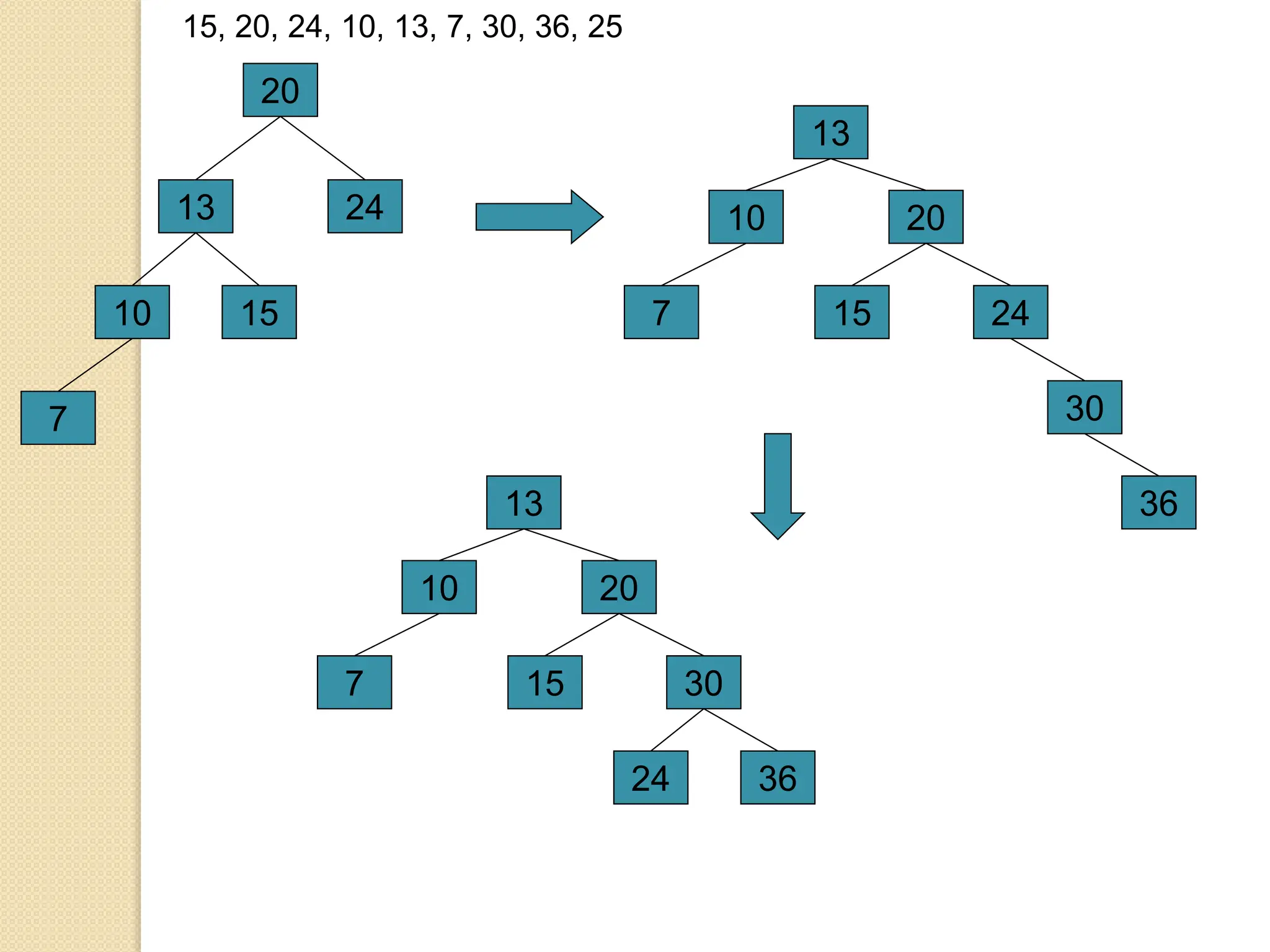
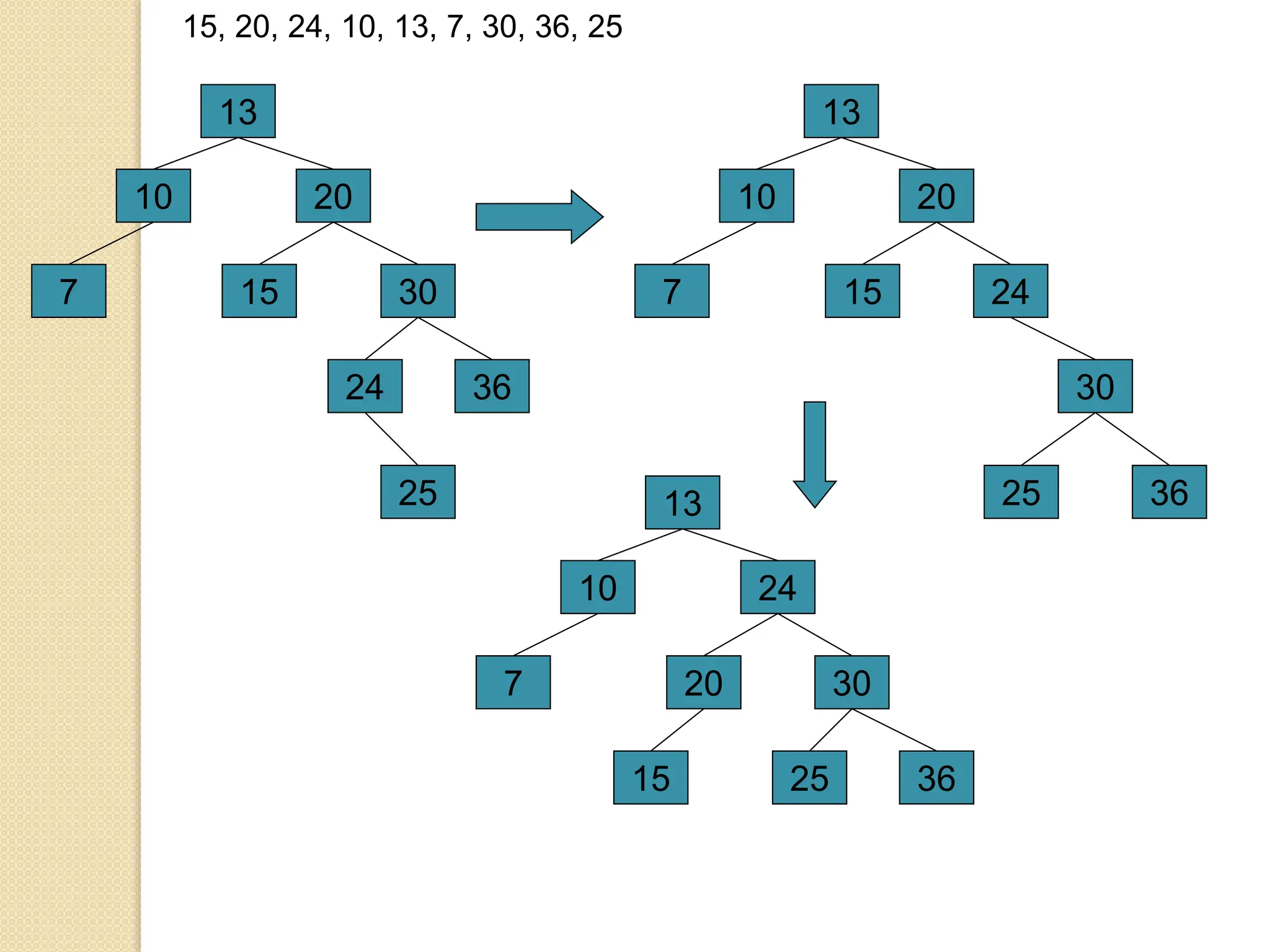
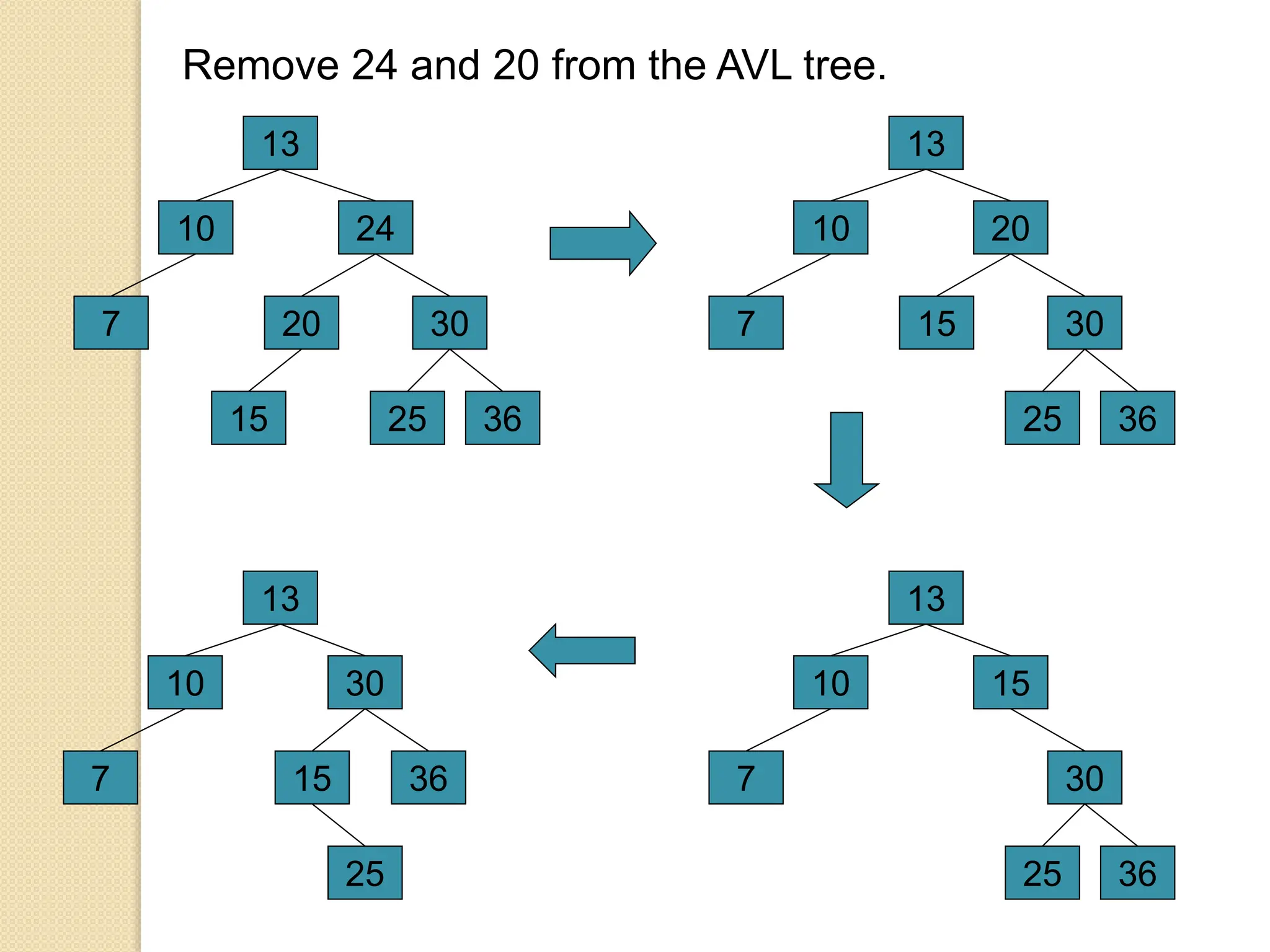
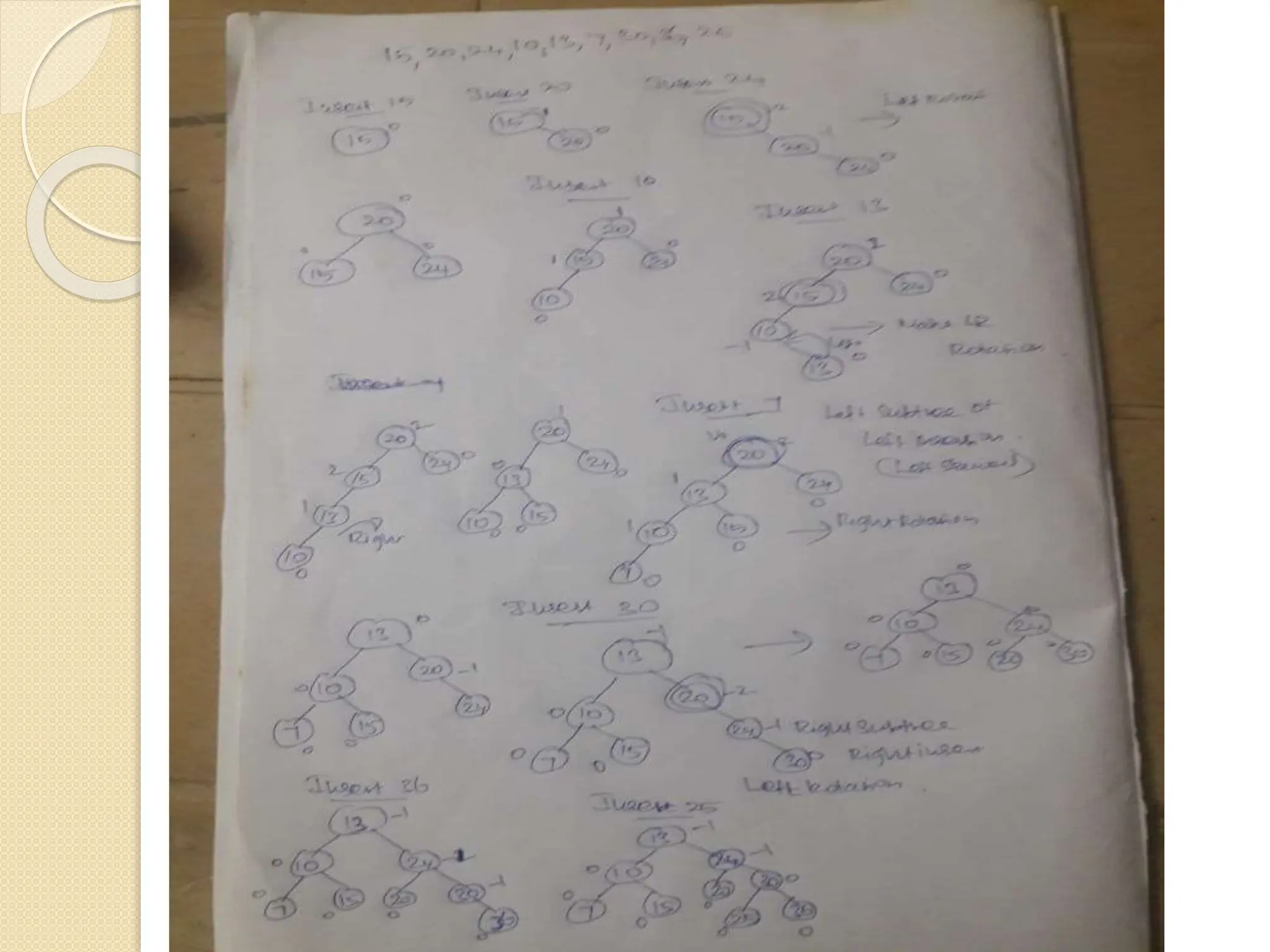
The document discusses AVL trees, which are self-balancing binary search trees. It describes how AVL trees maintain a balance factor of -1, 0, or 1 through rotations. It covers insertion, deletion, and the different types of rotations performed to balance the tree. Examples are provided to illustrate insertion, deletion, and the resulting rotations. AVL trees provide logarithmic time performance for operations by keeping the tree height balanced.

1. Data Structures
(AVL Tree)
Dr.N.S.Nithya
ASP/CSE

2. AVL Tree
 The AVL stands for Adelson-
Velskii and Landis, who are the
inventors of the AVL tree.AVL tree is a
self-balancing binary search tree in
which heights of the left sub trees and
right sub trees of any node differ by at
most one.

3. Balancing Factor
 Balance factor=height of left sub tree –
height of the right sub tree.
 The value of balance factor should always
be -1, 0 or +1.

4. Need for height balanced
trees
 If the binary search tree is either left skewed or
right skewed(not balanced) , the searching time
will be increased. Because searching time
depends upon the height of the tree. h=log(n)
where h is the height of the tree and n is the
number of nodes in the binary tree.It takes
log(n) for searching.

5. Balancing Factor Routine
int BF(node *T)
{
int lh,rh;
if(T==NULL)
return(0);
if(T->left==NULL)
lh=0;
else
lh=1+T->left->ht;
if(T->right==NULL)
rh=0;
else
rh=1+T->right->ht;
return(lh-rh);

6. Need for height balanced
trees
 The disadvantage of a binary search tree
is that its height can be as large as N-1
 This means that the time needed to
perform insertion and deletion and many
other operations can be O(N) in the worst
case
 We want a tree with small height
 A binary tree with N node has height at
least Q(log N)
 Thus, our goal is to keep the height of a
binary search tree O(log N)
 Such trees are called balanced binary

7. How to balanace AVL tree (Rotation)
 An insertion or deletion may cause an
imbalance in an AVL tree.
 An AVL tree causes imbalance when
any of following condition occurs:
 i. An insertion into Right child’s right
subtree.
 ii. An insertion into Left child’s left subtree.
 iii. An insertion into Right child’s left
subtree.
 iv. An insertion into Left child’s right
subtree.

8. How to balanace AVL tree (Rotation)
 Whenever the tree becomes imbalanced due to
any operation we use rotation operations to
make the tree balanced.
 Rotation is the process of moving nodes
either to left or to right to make the tree
balanced.

9. Single Left Rotation (LL Rotation)
 If a tree becomes unbalanced, when a node is
inserted into the right subtree of the right
subtree, then we perform a single left rotation .
 If BF(node) = +2 and BF(node -> left-child) = +1, perform LL
rotation.

10. Single Right Rotation (RR Rotation)
 AVL tree may become unbalanced, if a node
is inserted in the left subtree of the left
subtree. The tree then needs a right rotation.
 If BF(node) = -2 and BF(node -> right-child) = 1, perform RR
rotation.


11. node * rotateright(node *x)
{
node *y;
y=x->left;
x->left=y->right;
y->right=x;
x->ht=height(x);
y->ht=height(y);
return(y);
}
node * rotateleft(node *x)
{
node *y;
y=x->right;
x->right=y->left;
y->left=x;
x->ht=height(x);
y->ht=height(y);
return(y);
}

12. Left Right Rotation (LR Rotation)
(Double Rotation)
 AVL tree may become unbalanced, if a node is inserte
the left subtree of the right subtree .The tree needs
Rotation is a sequence of single left rotation followed
single right rotation.
 If BF(node) = -2 and BF(node -> right-child) = +1, perform RL rotation.

13. Right Left Rotation (RL Rotation)
(Double Rotation)
 AVL tree may become unbalanced, if a node is
inserted in the right subtree of the left subtree
.The tree needs The RL Rotation is sequence
of single right rotation followed by single left
rotation.
 If BF(node) = +2 and BF(node -> left-child) = -1, perform LR
rotation.

14. node * RR(node *T) //insert right subtree of right
{
T=rotateleft(T);
return(T);
}
node * LL(node *T) //insert left subtree of left
{
T=rotateright(T);
return(T);
}
node * LR(node *T) // insert left subtree of right
{
T->left=rotateleft(T->left);
T=rotateright(T);
return(T);
}
node * RL(node *T) //insert right subtree of left
{
T->right=rotateright(T->right);
T=rotateleft(T);
return(T);
}

15. Left Rotation
Right Rotation

16. Left-Right Rotation

17. Right-Left Rotation

18. Operations on an AVL Tree
 The following operations are performed
on AVL tree...
 Search
 Insertion
 Deletion
 search operation is similar to Binary
search tree.

19. Insertion Operation in AVL Tree
 Step 1 - Insert the new element into the
tree using Binary Search Tree insertion
logic.
 Step 2 - After insertion, check
the Balance Factor of every node.
 Step 3 - If the Balance Factor of every
node is 0 or 1 or -1 then go for next
operation.
 Step 4 - If the Balance Factor of any
node is other than 0 or 1 or -1 then that
tree is said to be imbalanced. In this
case, perform suitable Rotation to make
it balanced and go for next operation.

20. Rotating conditions
 If BF(node) = +2 and BF(node -> left-child) =
+1, perform LL rotation.
 If BF(node) = -2 and BF(node -> right-child) =
1, perform RR rotation.
 If BF(node) = -2 and BF(node -> right-child) =
+1, perform RL rotation.
 If BF(node) = +2 and BF(node -> left-child) =
1, perform LR rotation.

21. An Extended Example
Insert 3,2,1,4,5,6,7, 16,15,14
3
Fig 1
3
2
Fig 2
3
2
1
Fig 3
2
1
3
Fig 4
2
1
3
4
Fig 5
2
1
3
4
5
Fig 6
Single rotation
Single rotation
Insert 3 Insert 2
Insert 1
Insert 4
Insert 5
0
1
0
1
0
2 0
0 0
-
1
-1
0
0
-
2
-
2
-
1 0
0

22. 2
1
4
5
3
Fig 7 6
2
1
4
5
3
Fig 8
4
2
5
6
1 3
Fig 9
4
2
5
6
1 3
7
Fig 10
4
2
6
7
1 3
5
Fig 11
Single rotation
Single rotation
Insert 6
Insert 7
-1
0
0
0
0
0
0
0
-1
-
1
-
2
0
-
1
0
0
0
0
-
1
0
0
0
-
2
-
1
0
0
1
0
0
0
0
0
0

23. 4
2
6
7
1 3
5 16
Fig 12
4
2
6
7
1 3
5 16
15
Fig 13
4
2
6
15
1 3 5
16
7
Fig 14
Double rotation
Insert 16
Insert 15
-1
-
1
-1
0
0
0
0
0
-
2
-
1
-2
-
1
0
1
0
0
0
-
1
0
0
0
-
1
0
0
0
0

24. 5
4
2 7
15
1 3 6
16
14
Fig 16
4
2
6
15
1 3 5
16
7
14
Fig 15
Double rotation
Insert 14
-
2
-2
1
0
0
-1
0
0
0
0
-
1
0
0
0
0
1
0
0 0
0
1

25. Operations on an AVL Tree
 The following operations are performed
on AVL tree...
 Search
 Insertion
 Deletion
 search operation is similar to Binary
search tree.

26. node * insert(node *T,int x)
{
if(T==NULL)
{
T=(node*)malloc(sizeof(node));
T->data=x;
T->left=NULL;
T->right=NULL;
}
else
if(x > T->data) // insert in right subtree
{
T->right=insert(T->right,x);
if(BF(T)==-2)
if(x>T->right->data)
T=RR(T);
else
T=RL(T);
}

27. else
if(x<T->data)
{
T->left=insert(T->left,x);
if(BF(T)==2)
if(x < T->left->data)
T=LL(T);
else
T=LR(T);
}
T->ht=height(T);
return(T);
}

28. Deletion in AVL Trees
 Step 1: Find the element in the tree.
 Step 2: Delete the node, as per the
BST Deletion.
 Step 3: Two cases are possible:-
 Case 1: Deleting from the right subtree.
 Case 2: Deleting from left subtree.

29. Case 1: Deleting from the right
subtree.
 1A. If BF(node) = +2 and BF(node ->
left-child) = +1, perform LL rotation.
 1B. If BF(node) = +2 and BF(node ->
left-child) = -1, perform LR rotation.
 1C. If BF(node) = +2 and BF(node ->
left-child) = 0, perform LL rotation.

30. Case 2: Deleting from left subtree.
 2A. If BF(node) = -2 and BF(node ->
right-child) = -1, perform RR rotation.
 2B. If BF(node) = -2 and BF(node ->
right-child) = +1, perform RL rotation.
 2C. If BF(node) = -2 and BF(node ->
right-child) = 0, perform RR rotation.

31. AVL Tree Example:
• Now remove 53(leaf Node)
14
17
7
4
53
11
12
8 13

32. AVL Tree Example:
• Now remove 53, unbalanced
14
17
7
4
11
12
8 13

33. AVL Tree Example:
• Balanced! Remove 11(node with two
children)
14
17
7
4
11
12
8
13

34. AVL Tree Example:
• Remove 11, replace it with the largest in its left
branch tree balanced
14
17
7
4
8
12
13

35. AVL Tree Example:
• Remove 8(place with inorder predessor)replace
with largest element in the left subtree, unbalanced
14
17
4
7
12
13

36. AVL Tree Example:
• Remove 8, unbalanced
14
17
4
7
12
13

37. AVL Tree Example:
• Balanced!!
14
17
4
7
12
13

38. node * Delete(node *T,int x)
{
node *p;
if(T==NULL)
{
return NULL;
}
else
if(x > T->data) // delete in right
subtree
{
T->right=Delete(T->right,x);
if(BF(T)==2)
if(BF(T->left)>=0)
T=LL(T);
else

39. if(x<T->data)
{
T->left=Delete(T->left,x);
if(BF(T)==-2) //Rebalance
during windup
if(BF(T->right)<=0)
T=RR(T);
else
T=RL(T);
}

40. else
{
//data to be deleted is found
if(T->right!=NULL)
{ //delete its inorder succesor
p=p->right;
while(p->left!= NULL)
p=p->left;
T->data=p->data;
T->right=Delete(T->right,p->data);
if(BF(T)==2)//Rebalance during windup
if(BF(T->left)>=0)
T=LL(T);
else
T=LR(T);
}
else
return(T->left);
}
T->ht=height(T);
return(T);
}

41. Height calculation
int height(node *T)
{
int lh,rh;
if(T==NULL)
return(0);
if(T->left==NULL)
lh=0;
else
lh=1+T->left->ht;
if(T->right==NULL)
rh=0;
else
rh=1+T->right->ht;
if(lh>rh)
return(lh);
return(rh);

42. Applications of AVL Tree
 AVL trees are used for frequent insertion.
 It is used in Memory management
subsystem of linux kernel to search
memory regions of processes during
preemption.
 Sort the following database:
 Dictioonary
 Google search engine
 some sites to take data faster
 sites which have large amount of data
example is Facebook.

43. In Class Exercises
 Build an AVL tree with the following values:
15, 20, 24, 10, 13, 7, 30, 36, 25

44. 15
15, 20, 24, 10, 13, 7, 30, 36, 25
20
24
15
20
24
10
13
15
20
24
13
10
13
20
24
15
10

45. 13
20
24
15
10
15, 20, 24, 10, 13, 7, 30, 36, 25
7
13
20
24
15
10
7
30
36
13
20
30
15
10
7
36
24

46. 13
20
30
15
10
7
36
24
15, 20, 24, 10, 13, 7, 30, 36, 25
25
13
20
30
15
10
7
36
24
25
13
24
36
20
10
7
25
30
15

47. Remove 24 and 20 from the AVL tree.
13
24
36
20
10
7
25
30
15
13
20
36
15
10
7
25
30
13
15
36
10
7
25
30
13
30
36
10
7
25
15