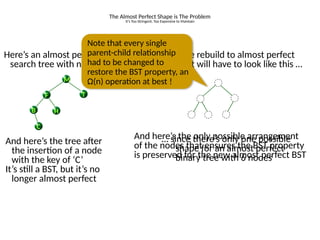
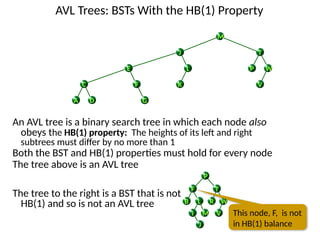
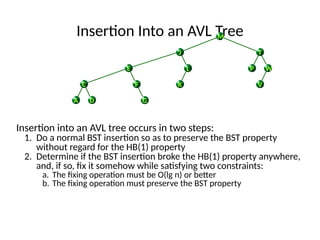
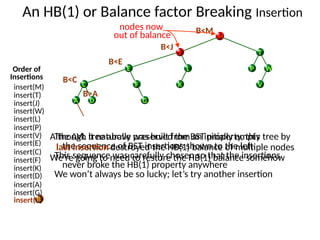
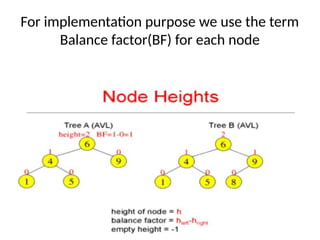
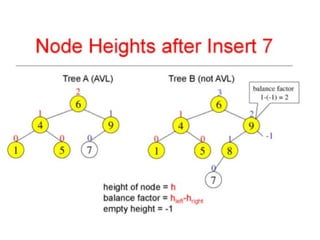
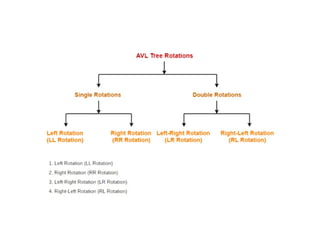
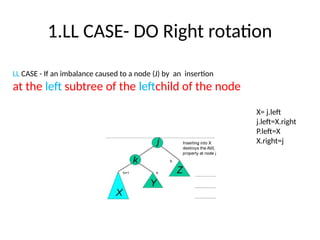
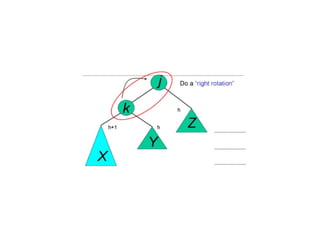
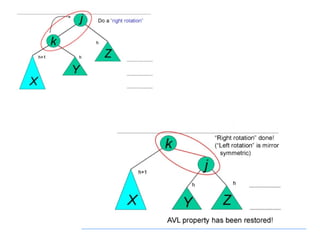
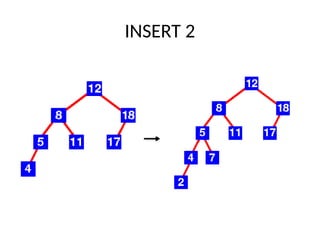
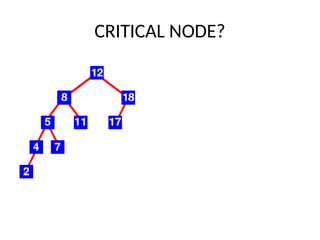
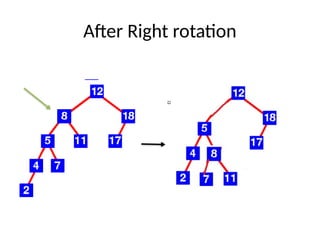
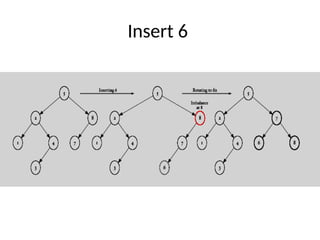
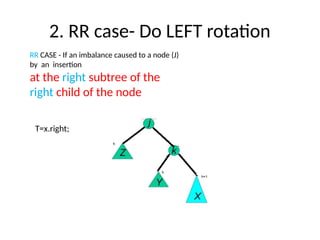
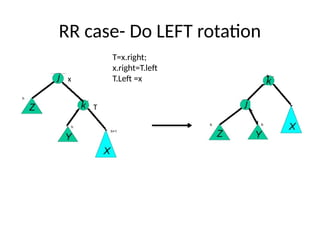
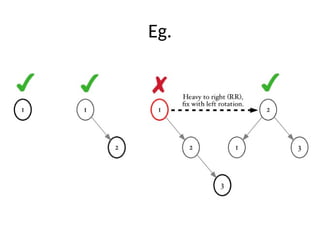
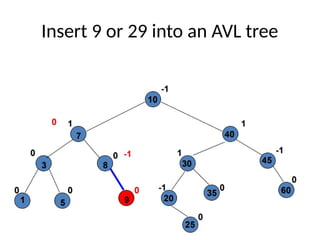
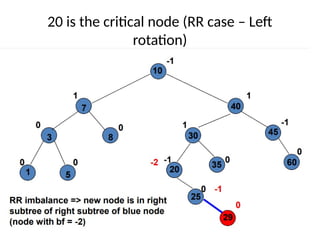
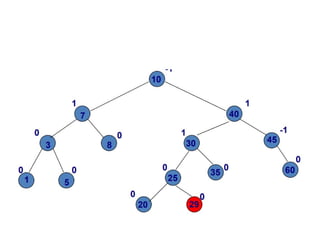
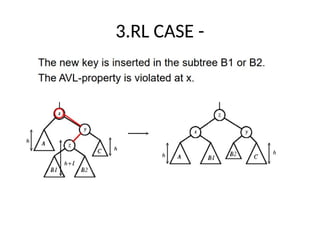
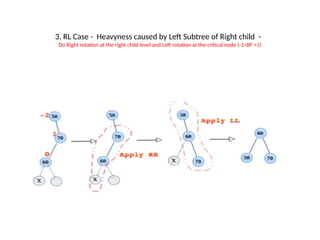
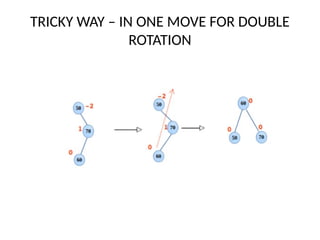
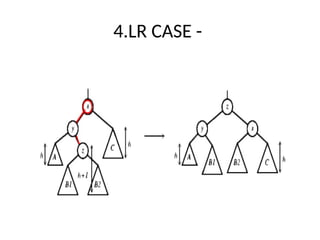
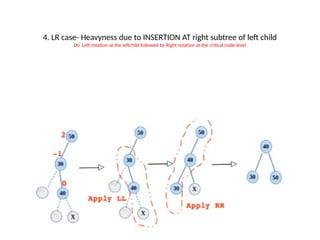
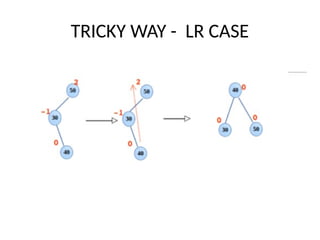
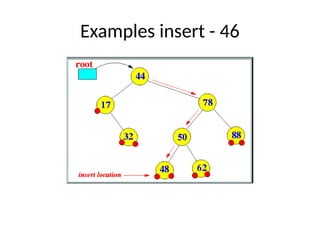
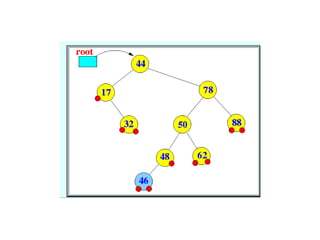
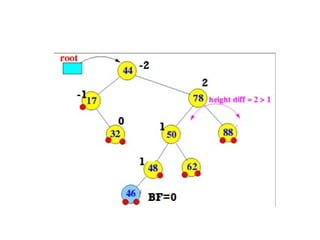
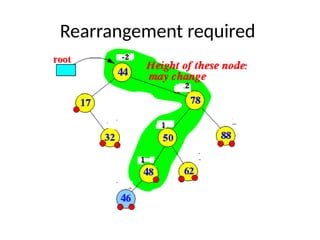
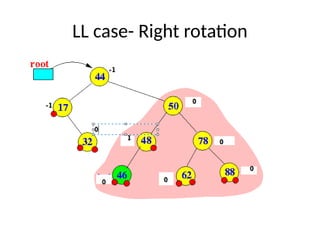
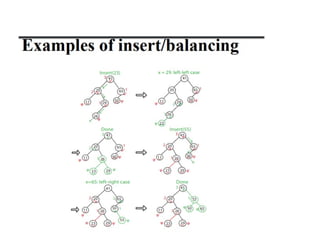
AVL trees are height-balanced binary search trees that maintain a height difference of at most one between left and right subtrees to ensure O(log n) search, insertion, and deletion operations. The insertion process involves a standard BST insertion followed by adjustments to restore the height balance using specific rotations, facilitating efficient structure maintenance. The AVL tree structure was developed by Georgy Adelson-Velsky and Evgenii Landis, representing a significant advancement in data structures and their theoretical foundations.