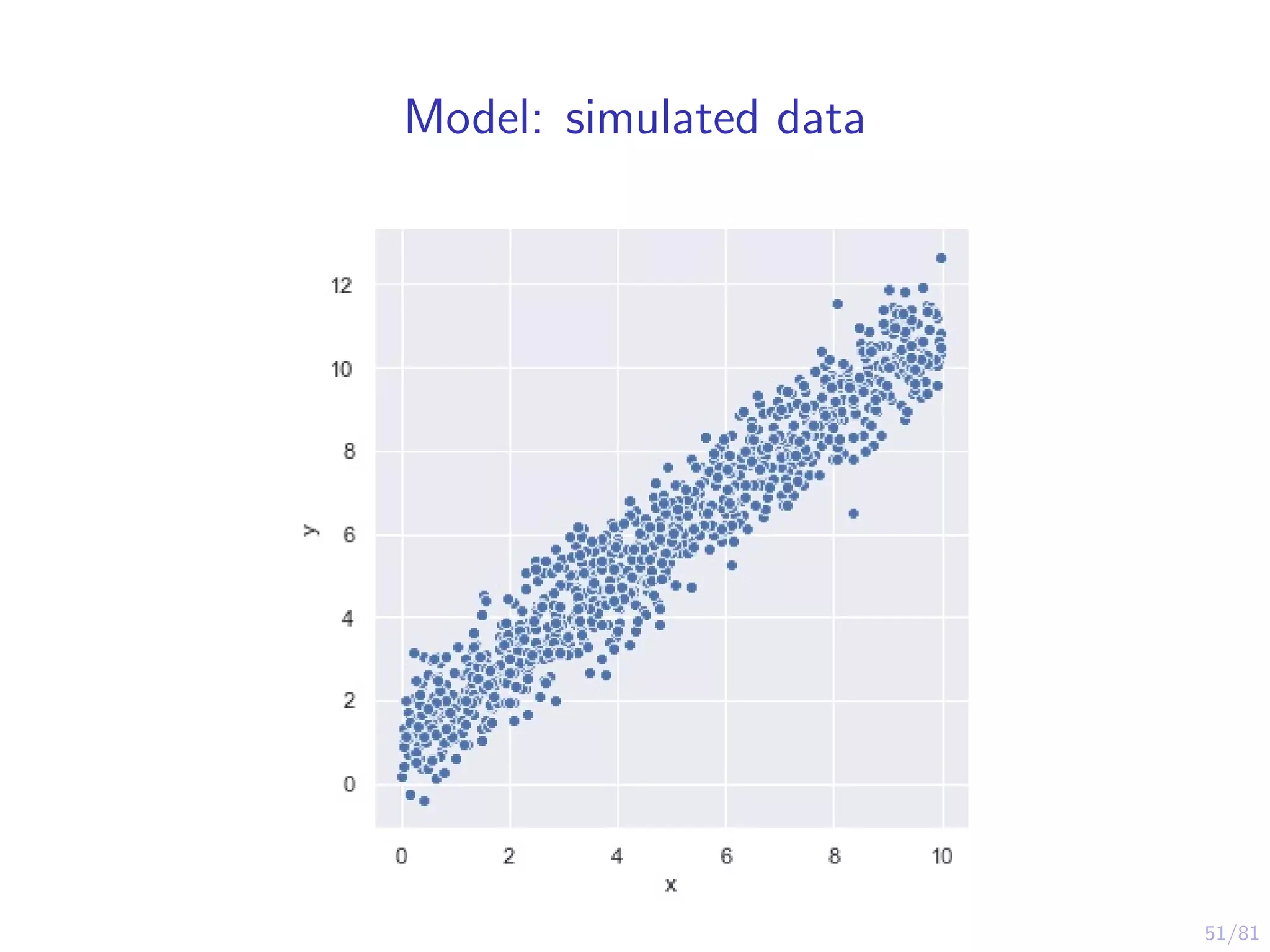
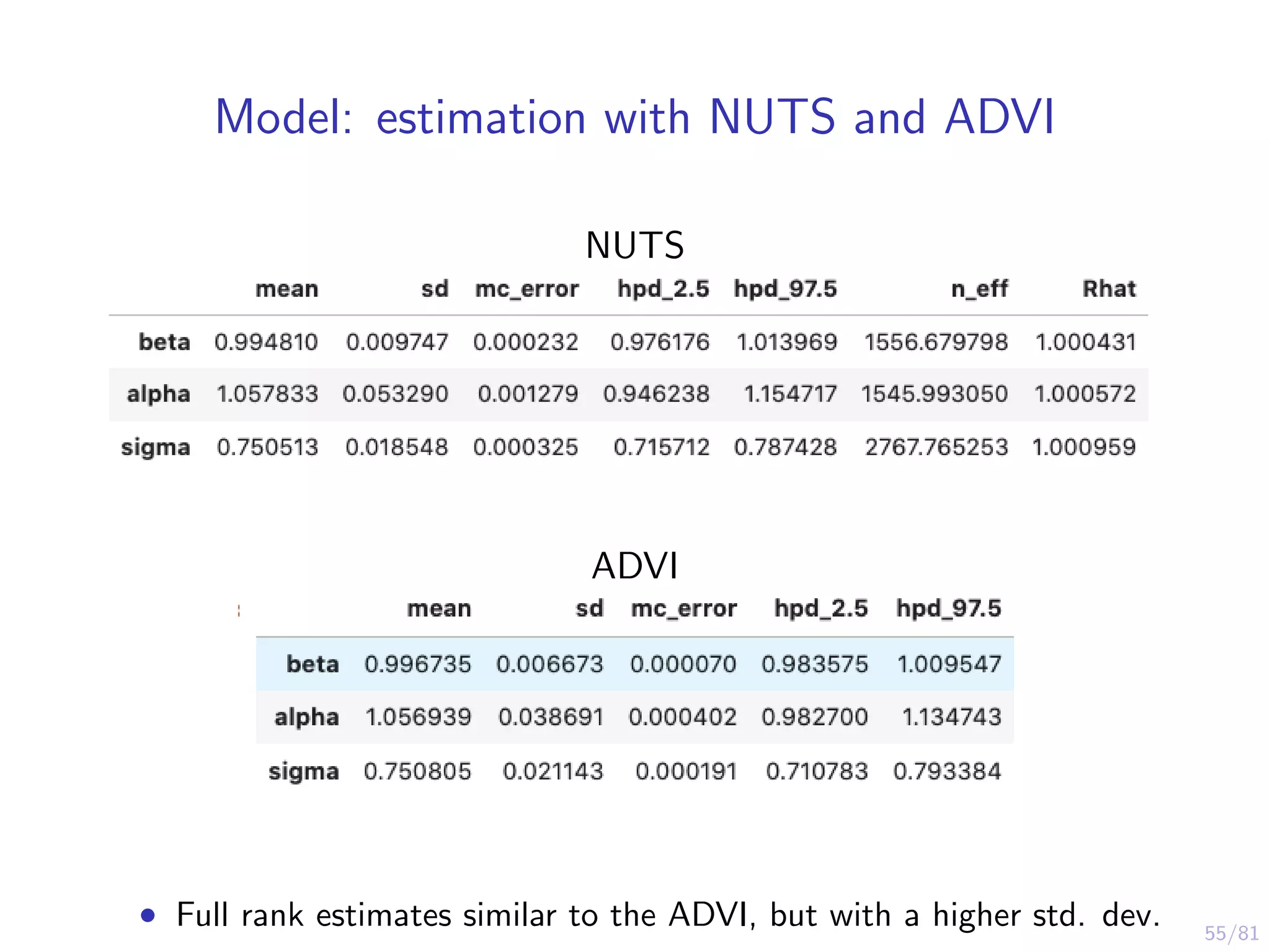
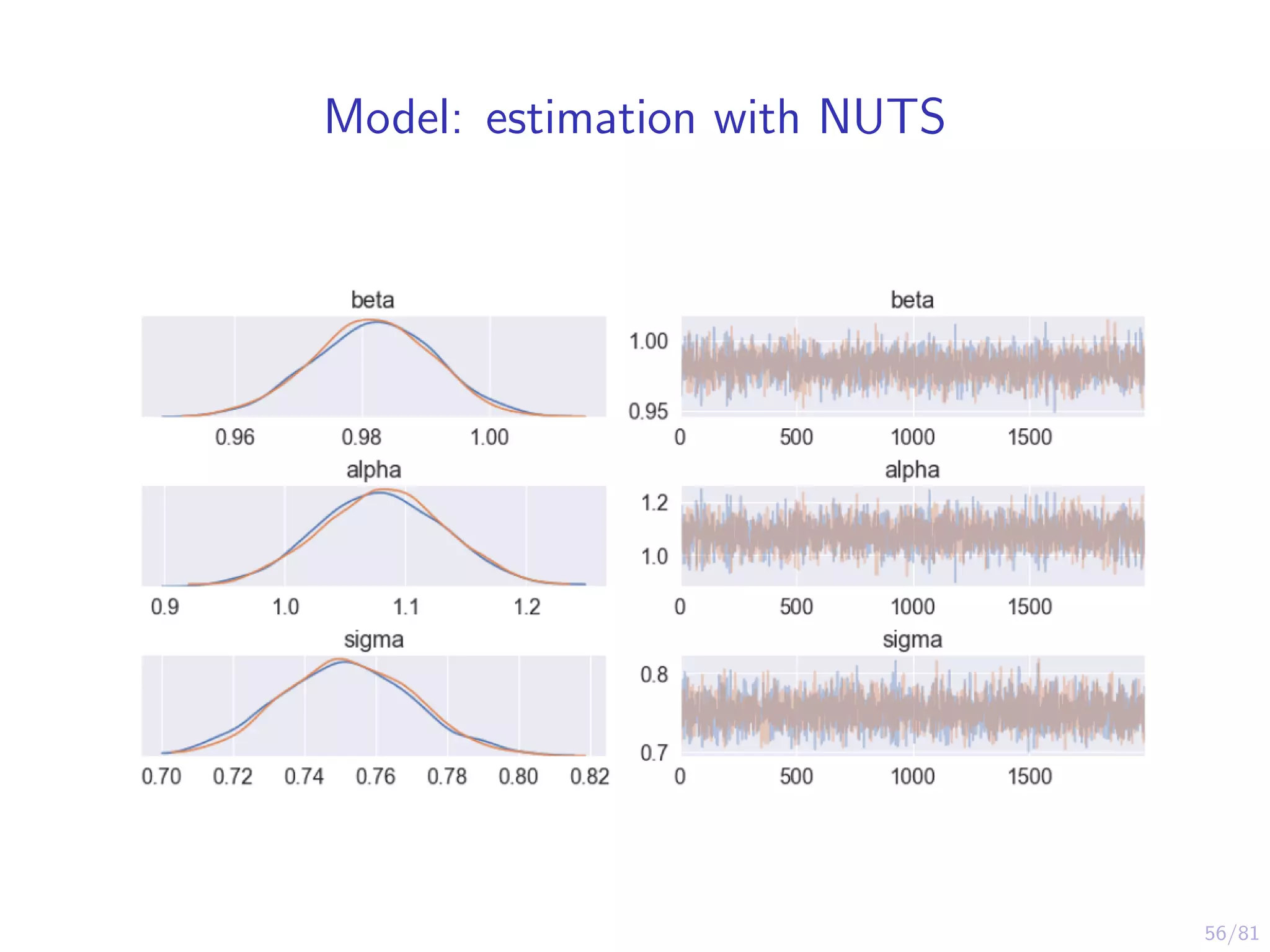
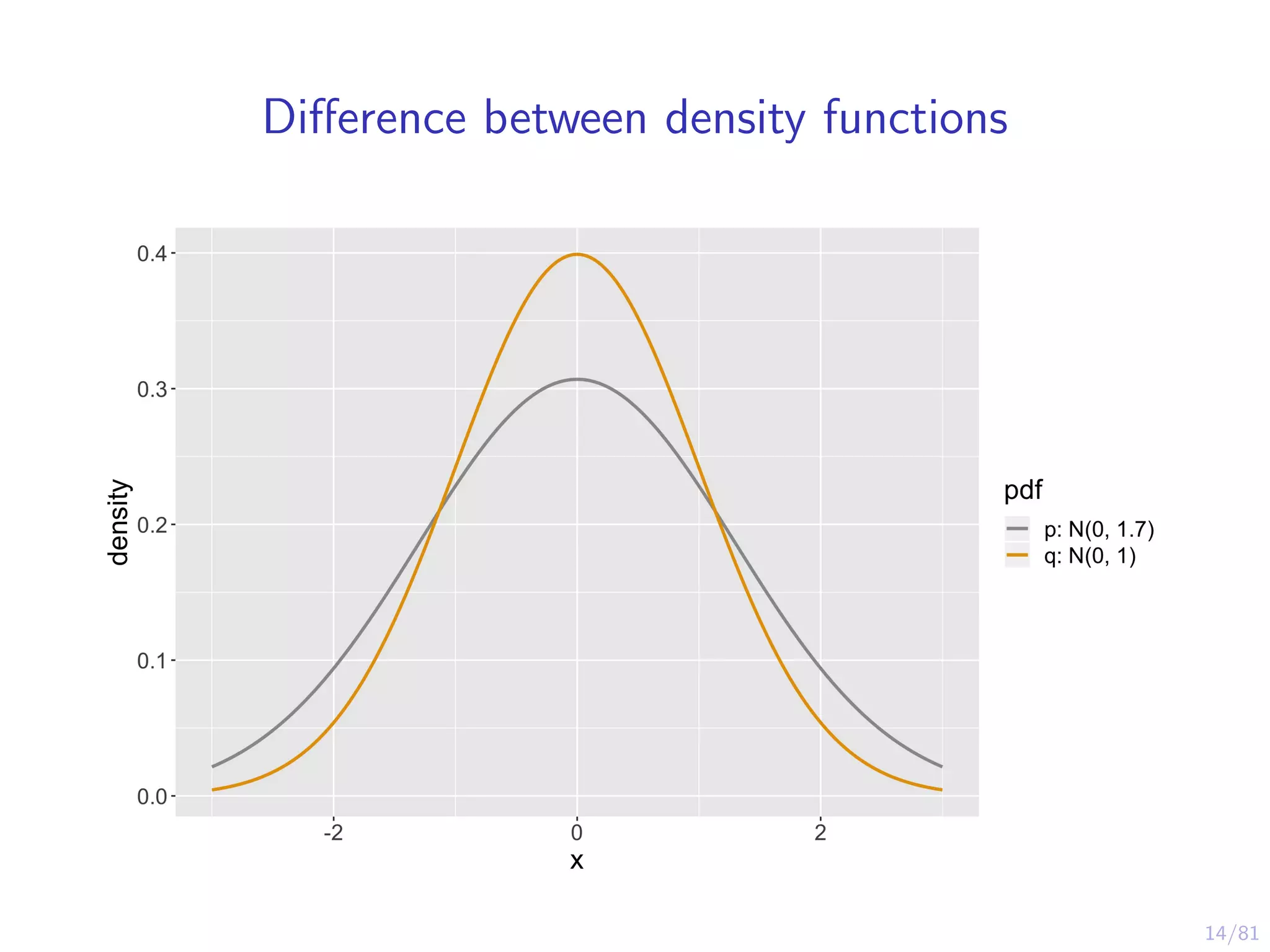
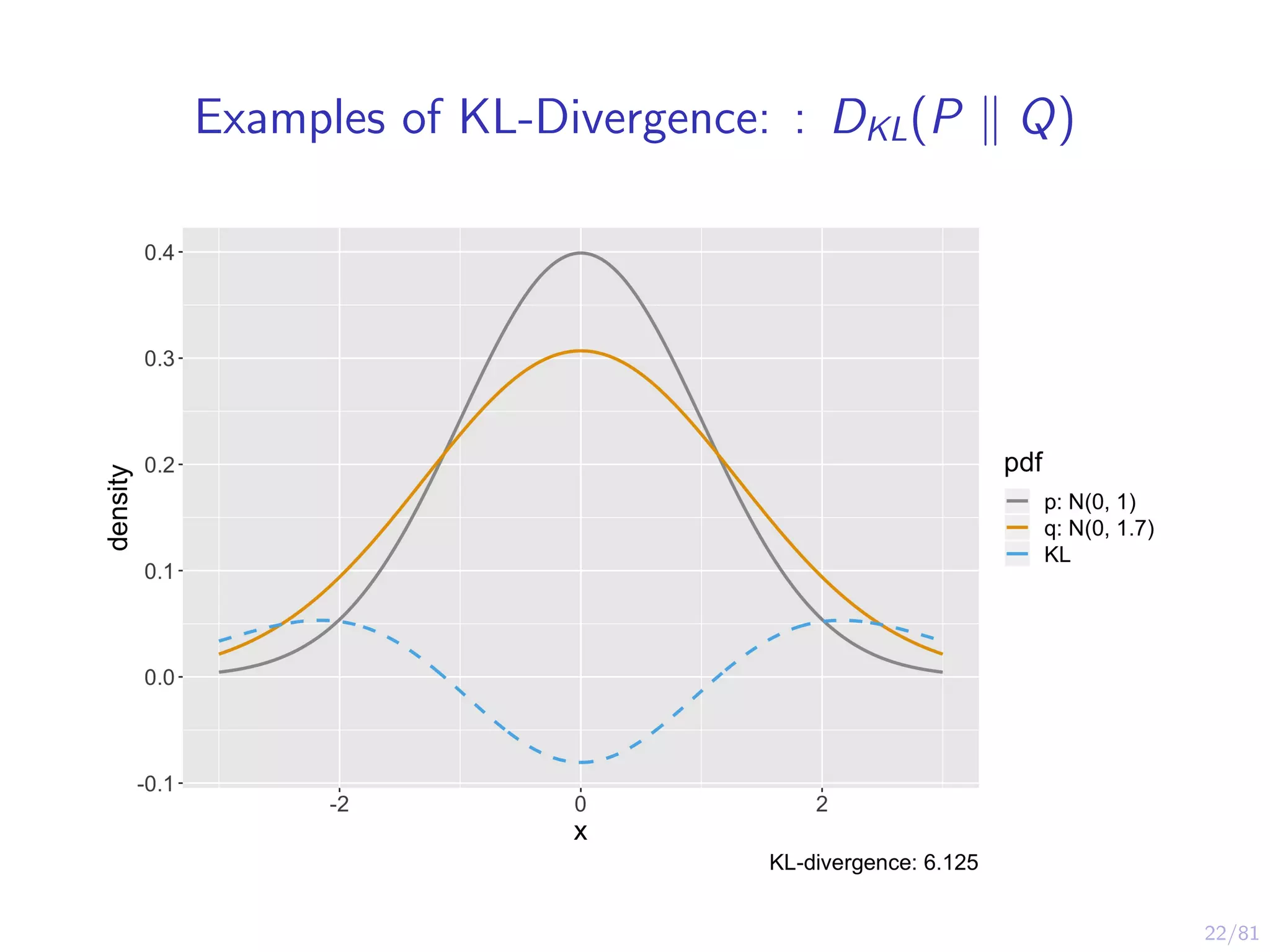
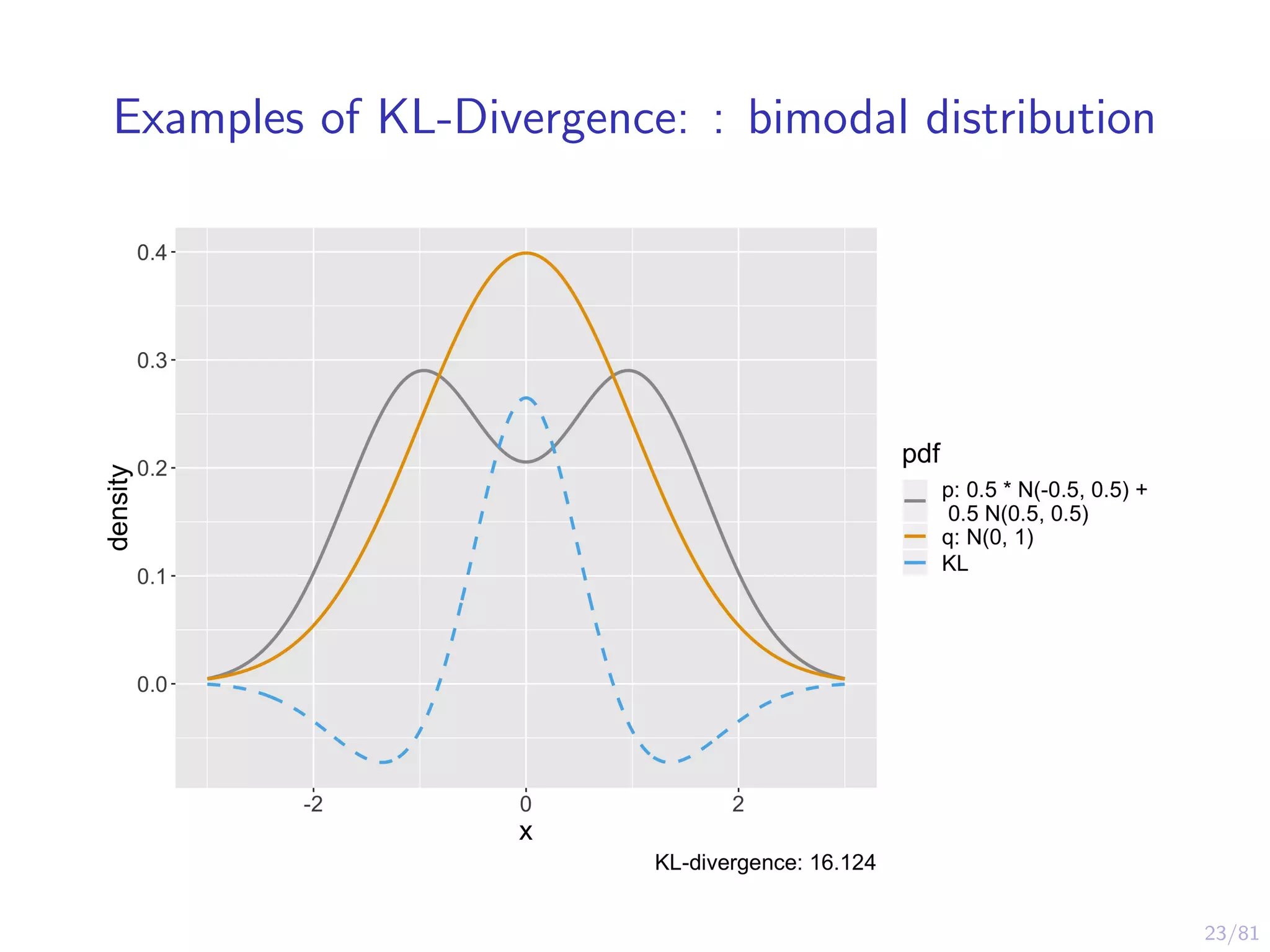
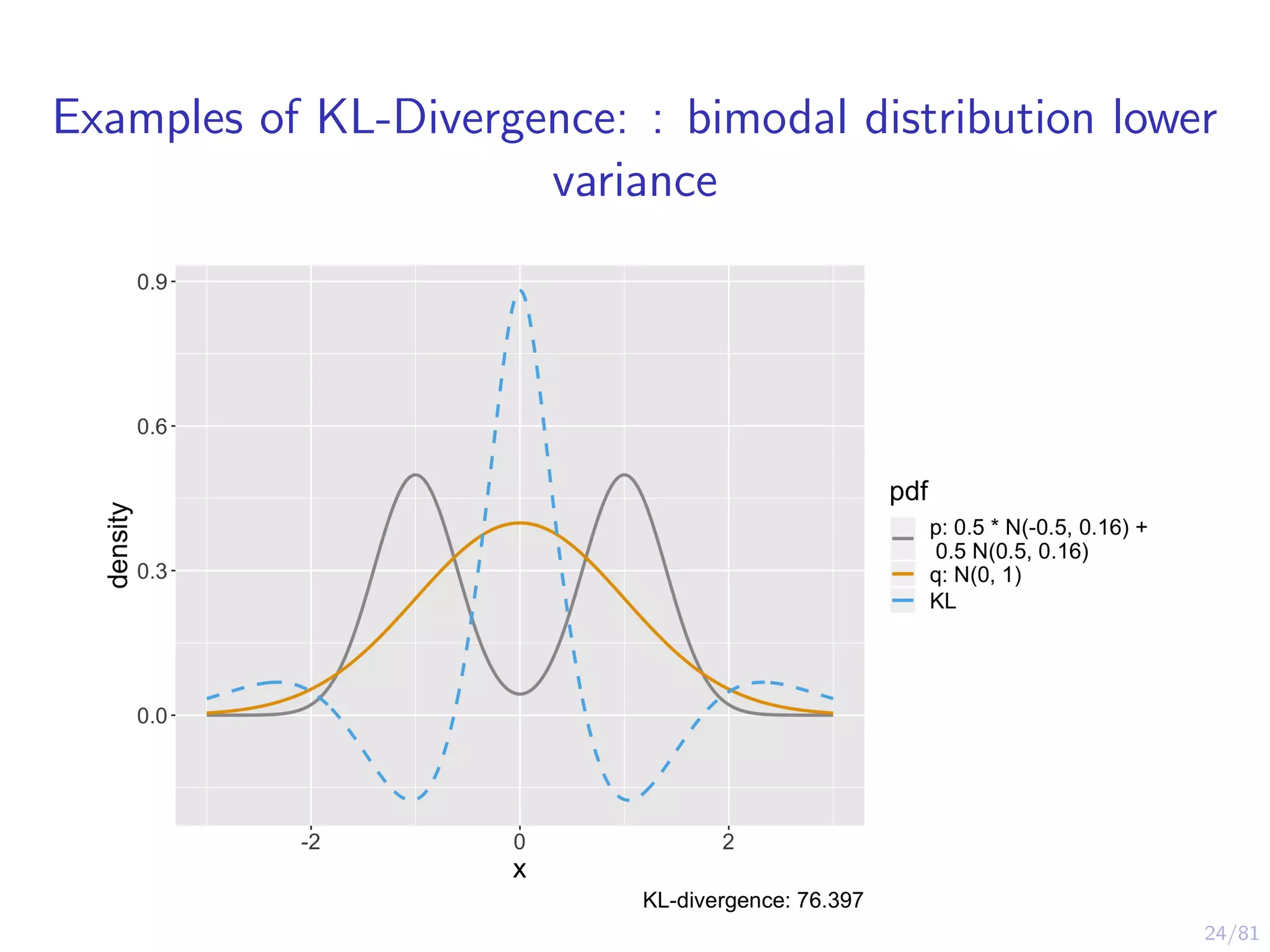
The document provides an introduction to Variational Bayes, outlining the fundamental concepts such as Bayesian inference, Kullback-Leibler divergence, and optimization strategies like Evidence Lower Bound (ELBO). It contrasts Variational Inference with traditional MCMC methods, emphasizing the speed advantages of the former while noting trade-offs in precision and understanding. Examples and algorithms are discussed, including implementations with libraries like PyMC3, aimed at making Bayesian computation more accessible.

1. Variational Bayes:
A Gentle Introduction
Flavio Mejia Morelli
December 3, 2019

2. 2/81
About me
• Flavio, from Bogot´a (Colombia)
• Education: MSc. Statistics at Humboldt University Berlin
• Work: statistical consulting unit of the Free University of
Berlin fu:stat

3. 3/81
About this talk
• Basic knowledge of probability theory
• Basic knowledge of Bayesian statistics
• Focus on intuition, from a learner’s perspective
• However, Bayesian computation is still very technical
• Feel free to ask questions during the talk!
• For the material, check @ flaviomorelli on Twitter

4. 4/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

5. 5/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

6. 6/81
Motivation: Why Variational Bayes?
• One of the main alternatives to MCMC
• Estimate different kinds of models much faster than MCMC
(usually at the expense of precision)
• However, variational inference is less well understood than
MCMC

7. 7/81
Terminology: Bayes’ theorem
p(θ|y) =
p(θ, y)
p(y)
=
p(y|θ) · p(θ)
Θ p(y|θ) · p(θ)dθ

8. 8/81
Terminology: Bayes’ theorem
p(θ|y) =
p(θ, y)
p(y)
=
p(y|θ) · p(θ)
Θ p(y|θ) · p(θ)dθ
• θ ∈ Θ: a parameter or vector of parameters (e.g. the
probability in a binomial distribution) in the parameter space
Θ
• y: data
• p(θ|y): posterior
• p(y|θ): likelihood function that captures how we are modeling
our data stochastically (e.g. y is a binomial variable)
• p(θ): prior knowledge about the parameters (e.g. a
probability can only be between 0 and 1)

9. 9/81
Terminology: Bayes’ theorem
p(θ|y) =
p(θ, y)
p(y)
=
p(y|θ) · p(θ)
Θ p(y|θ) · p(θ)dθ
• p(y) = Θ p(y|θ) · p(θ)dθ: the marginal likelihood or evidence
• p(y) is a constant that normalizes the expression so that the
posterior integrates to one.
• Problem: p(y) is intractable even for very simple models,
and this makes it very hard to calculate the posterior
• Bayesian computation methods get around this intractability
by different means

10. 10/81
MCMC and variational inference
• Markov Chain Monte Carlo (MCMC) is one of the most
common methods of estimating parameters in a Bayesian
model
• ”Little fly” takes samples from the parameter space to find
out how likely a given combination of parameters is
• Different approaches: Gibbs Sampler, Metropolis-Hastings,
Hamiltonian Monte Carlo, NUTS
• Pro: more Monte Carlo samples lead to a more accurate
estimate
• Con: slow and curse of dimensionality

11. 11/81
MCMC and variational inference
• Variational inference turn the estimation of the posterior into
an optimization problem (i.e. maximize or minimize)
• Main idea: find another probability function that is easier to
work with than the posterior
• Minimize the difference between the new probability function
an the posterior

12. 12/81
MCMC and variational inference
How do we measure the difference between
probability functions?

13. 13/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

14. 14/81
Difference between density functions

15. 15/81
Difference between density functions
• Let p(x) and q(x) be two probability densities
• A naive approach for a given x:
q(x)
p(x)

16. 16/81
Difference between density functions
• However, if we flip the terms we see that the absolute value of
this measure also changes: e.g. 0.3
0.1 = 3, but 0.1
0.3 = 1
3
• If we take the logarithm, the absolute value stays constant
after flipping the probabilities, only the sign changes:
log(q(x)
p(x) ) = −log(p(x)
q(x) )

17. 17/81
Difference between density functions
• Assume that we are interested mainly on q(x)
• Use q(x) as a weight for the difference measure: q(x)log(q(x)
p(x) )
• When q(x) is low, the difference measure log(q(x)
p(x) ) does not
matter as much, as when q(x) is high!

18. 18/81
Difference between density functions
• As a final step, we integrate over all the possible values of x
(or sum if the density is not continuous)
DKL = X q(x) log(q(x)
p(x) )dx
• DKL is called the Kullback-Leibler divergence of p from q

19. 19/81
Kullback-Leibler Divergence
DKL(q p) = X q(x) log(q(x)
p(x) )dx
• Common measure for the divergence between two probability
densities
• The Kullback-Leibler divergence is not symmetric, and thus
is cannot be called a ”distance”: DKL(q p) = DKL(p q)

20. 20/81
Kullback-Leibler Divergence
X q(x) log(q(x)
p(x) )dx = − X q(x) log(p(x)
q(x) )dx
• Note that if we flip the densities inside the logarithm, the
divergence does not change
• DKL ≥ 0 for any given probabilities. If DKL = 0 it means that
both probabilities are the same at each point

21. 21/81
Examples of KL-Divergence: DKL(Q P)

22. 22/81
Examples of KL-Divergence: : DKL(P Q)

23. 23/81
Examples of KL-Divergence: : bimodal distribution

24. 24/81
Examples of KL-Divergence: : bimodal distribution lower
variance

25. 25/81
Variational approximation of the posterior
• Find a q∗(θ) which minimizes the KL divergence between q(θ)
and the posterior p(θ|y):
DKL(q p) =
Θ
q(θ) log(
q(θ)
p(θ|y)
)
• However, in order to calculate the KL divergence we would
have to know the posterior p(θ|y) which is intractable.
• We are back to square one...

26. 26/81
Side note: What does ”variational” mean?
• The term ”variational” comes from variational calculus
• One of the main topics of calculus is optimization
• Optimization is usually done with respect to a variable.
• A common problem in economic is finding an optimum
quantity Q∗ that maximizes profit given a demand and a cost
function
• In contrast, variational calculus optimizes with respect to a
function. In our case, we are trying to find a q∗(θ) which
minimizes the Kullback-Leibler divergence

27. 27/81
Side note: KL-divergence as expected value
• Some papers and textbooks write the KL divergence as an
expected value with respect to q
• Because we are weighting by q(θ), we can express it as an
expected value
DKL(q p) =
Θ
q(θ) log
q(θ)
p(θ|y)
= Eq log
q(θ)
p(θ|y)

28. 28/81
So, what now?
Find an alternative way to optimize the
divergence!

29. 29/81
ELBO: evidence lower bound
• It can be shown that:
log p(y) =
Θ
q(θ) log
p(y, θ)
q(θ)
L
+
Θ
q(θ) log
q(θ)
p(θ|y)
DKL(q p)
• DKL(q p) is the Kullback-Leibler divergence
• L is the evidence lower bound
• The Kullback-Leibler divergence is intractable, because it
contains the posterior
• On the other hand, it is possible to compute all the terms in
L, as p(y, θ) = p(θ)p(y|θ) is known

30. 30/81
ELBO: derivation
log p(y) = log p(y) · 1 = log p(y)
Θ
q(θ)dθ
=
Θ
q(θ) log p(y)dθ =
Θ
q(θ) log
p(y, θ)
p(θ|y)
dθ
=
Θ
q(θ) log
p(y, θ)
p(θ|y)
·
q(θ)
q(θ)
dθ
=
Θ
q(θ) log
p(y, θ)
q(θ)
+
Θ
q(θ) log
q(θ)
p(θ|y)
Which can be written as (Ormerod & Wand, 2010):
log p(y) = L + DKL(q p)

31. 31/81
ELBO: importance and optimization
• By rearranging we get:
L = log p(y) − DKL(q p)
• As DKL ≥ 0 ⇒ log p(y) ≥ L
• Therefore, L is the lower bound of the logarithm of the
evidence p(y)
• Hence the name evidence lower bound or ELBO for L

32. 32/81
ELBO: importance and optimization
L = log p(y) − DKL(q p)
• Key idea: Maximizing the ELBO is equivalent to minimizing
the Kullback-Leibler divergence
• The idea of maximizing the ELBO is the basis of most
variational inference approaches

33. 33/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

34. 34/81
Making the ELBO tractable
• In theory, we could take any distribution q we like to
approximate the posterior
• However, there are usually restrictions on q to make the
problem more tractable

35. 35/81
Making the ELBO tractable
• The most common restrictions are (Ormerod & Wand, 2010):
• Mean-field assumption: q(θ) factorizes into
M
i=1 qi (θi ) for
some partition {θ1, ..., θM }
• q comes from a parametric family of density functions

36. 36/81
Mean-field assumption
q(θ) = M
i=1 qi (θi )
• E.g. normal distribution: p
µ
σ
= p(µ)p(σ)
• Note that the quality of the approximation depends on the
dependence between θi
• Example: given p(θ1, θ2|y), if θ1 and θ2 are highly dependent,
then the restriction q(θ1, θ2) = q1(θ1)q2(θ2) will cause a
degradation in the inference

37. 37/81
Mean-field assumption
• The graphic shows a mean-field approximation of a
two-dimensional Gaussian posterior (Blei, Kucukelbir, & McAuliffe,
2017)
• Both distribution share the same mean, but the covariance
structure is different

38. 38/81
Coordinate ascent variational inference: algorithm
1 Initialize q∗
2(θ2), ..., q∗
M(θM)
2 Cycle
q∗
1(θ1) =
exp{ E−θ1 log p(y, θ)}
exp{E−θ1 log p(y, θ)}dθ1
.
.
.
q∗
M(θM) =
exp{ E−θM
log p(y, θ)}
exp{E−θM
log p(y, θ)}dθM
Until the increase in the ELBO is negligible (Ormerod & Wand,
2010)

39. 39/81
Coordinate ascent variational inference: key takeaways 1
• The algorithm is very inefficient, since is it use the complete
data set for each time it updates q∗
i (θi ), and then repeats
until ELBO converges
• This means CAVI cannot handle massive data

40. 40/81
Coordinate ascent variational inference: key takeaways 2
• The ELBO or the optimal solution for q∗
i have to be
calculated by hand for each model
• There are good examples of the mathematical derivation
(with Python implementation) for a univariate Gaussian model
(Sia, 2019)
• Another example for the mathematical derivation of the
ELBO can be found in the original paper on Latent Dirichtlet
Allocation, a topic model algorithm (Blei, Ng, & Jordan, 2003)

41. 41/81
Coordinate ascent variational inference: key takeaways 3
• This approach only works for conditionally conjugate
models like multilevel regression (e.g. linear, probit, Poisson),
matrix factorization (e.g. factor analysis, PCA),
mixed-membership models (e.g. LDA), etc. (Blei, 2017)
• There is a relation between the CAVI and Gibbs-Sampling
(Ormerod & Wand, 2010)

42. 42/81
Stochastic Variational approximation (SVI)
• Based on stochastic approximation (Robbins & Monro, 1951)
• On each iteration: take a subsample of the data, infer the
local structure, update the global structure, repeat
• The gradient is noisy, but it is still doing the coordinate
ascent on the ELBO
• More efficient than CAVI, and more accurate results (Blei,
2017)

43. 43/81
Stochastic Variational approximation (SVI): disadvantages
• Still has to be derived analytically
• Still limited to the same types of model that worked with CAVI

44. 44/81
Black box variational inference: motivation
• CAVI and SVI problems:
• Problem # 1: Time-consuming For each model, you have
to derive the formulas analytically, and then come up with an
algorithm to calculate the model
• Problem # 2: Lack of generalization What happens to
models that are not conditionally conjugate? (Bayesian logistic
regression cannot be easily estimated with CAVI or SVI!)

45. 45/81
Black box variational inference: goal
• Goal: Use variational inference with any model
• No mathematical work besides specifying the model
• Most Bayesian packages and languages (Stan, PyMC3,...) use
this kind of variational inference to estimate the model (e.g.
ADVI)

46. 46/81
Black box variational inference: how does it work?
• Noisy gradient of the ELBO, λ is a hyperparameter (Ranganath,
Gerrish, & Blei, 2014):
λL = Eq[( λlog q(θ|λ))(log p(y, θ) − log q(θ|λ))]
• q(θ|λ) is from the variational families and can be stored in a
library
• p(y, θ) = p(θ)p(y|θ) is equivalent to writing down the model
• Black box criteria:
• Sample from q(θ|λ) (Monte Carlo)
• Evaluate λlog q(θ|λ)
• Evaluate log p(y, θ)

47. 47/81
Black box variational inference: key takeaways
• q(θlλ) (variational approximation) and p(y, θ) (our model)
are known
• Only this two components are needed to calculate the
gradient, and maximize the ELBO
• No time-consuming analytical derivation needed
• Makes it possible to estimate a wider range of models e.g.
GLM, nonlinear time series, volatility models (e.g. ARCH,
GARCH), Bayesian neural networks (Blei, 2017)

48. 48/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

49. 49/81
Model: univariate linear regression
y = α + βx
y ∼ N(α + βx, σ)
α ∼ G−1(1, 1)
β ∼ N(0, 2)
σ ∼ G−1(1, 1)
• Note that the normal distribution is parametrized with the
standard deviation
• This examples is based on (Ioannides, 2018)

50. 50/81
Model: true parameters
• The data is generated by simulation
• True parameters:
α = 1
β = 1
σ = 0.75

51. 51/81
Model: simulated data

52. 52/81
Model: code

53. 53/81
Model: estimation with NUTS

54. 54/81
Model: estimation with ADVI
• It is also possible to use minibatches (PyMC3 documentation)
• Use ”fullrank advi” to keep the correlation structure

55. 55/81
Model: estimation with NUTS and ADVI
NUTS
ADVI
• Full rank estimates similar to the ADVI, but with a higher std. dev.

56. 56/81
Model: estimation with NUTS

57. 57/81
Model: estimation with ADVI

58. 58/81
Model: maximizing the ELBO

59. 59/81
Correlation in MCMC
• In a linear regression, the fitted line goes through y and x
• The intercept and the slope are negatively correlated
• A higher slope means that the intercept has to adjust
downwards

60. 60/81
Correlation in ADVI (mean-field)
• With ADVI, there is no correlation due to the mean-field
assumption

61. 61/81
Correlation in Full Rank ADVI
• Full rank ADVI takes into account the covariance structure
of the model
• However, it can take longer to estimate

62. 62/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

63. 63/81
Evaluating variational inference
• It can be challenging to discover problems with posterior
approximation (Yao, Vehtari, Simpson, & Gelman, 2018)
• Variational inference approaches come with few theoretical
guarantees
• It is difficult to assess the quality of the approximation

64. 64/81
Evaluating variational inference
• Usual problems (Blei et al., 2017):
• Slow ELBO convergence
• The inability of the approximation family to capture the true
posterior
• The mean-field assumption makes it difficult to calculate
posterior correlation
• The asymmetry of the true distribution
• KL divergence under-penalizes approximations with too light
tails

65. 65/81
Diagnostics in common Bayesian frameworks
• Both Stan and PyMC3 use ADVI (Kucukelbir, Tran, Ranganath,
Gelman, & Blei, 2017), which is related to Black Box variational
inference
• Both frameworks have convergence diagnostics (in Stan
there is still an open pull request to impolement all the
diagnostics from the Yao et al. paper)

66. 66/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

67. 67/81
Issues with KL-divergence
• The KL divergence punishes placing mass in q where p has
little mass, but it punishes less the reverse
• The mean-field assumption can lead to underestimate the
posterior variance, and to miss important modes (Blei et al.,
2017).
• However, there is fullrank ADVI which helps capture
parameter correlations (e.g. in PyMC3, Stan)
• There are alternative divergence measures (e.g.
α-divergence), but their use is still an open question

68. 68/81
Alternatives divergence measures: Expectation
maximization
• Why don’t we minimize DKL(p q), which would be more
intuitive?
DKL(p q) =
Θ
p(θ|y) log(
p(θ|y)
q(θ)
)
• This alternative is also feasible and it is called expectation
maximization
• However, it is less efficient than minimizing DKL(q p) (Blei et
al., 2017)

69. 69/81
Alternatives divergence measures: α-divergence and tail
adaptive f -divergence
• α-divergence: typically larger values of α enforce stronger
mass-covering, i.e. approximation q covers more modes of p
(Minka, 2005)
• Tail adaptive f -divergence: offers a solution to the problem
that the α-divergence might cause high or infinite variance
when the distributions have fat tails (Wang, Liu, & Liu, 2018)

70. 70/81
Alternatives divergence measures in practice
• Alternative divergences can lead to better approximations, but
can be more difficult to estimate
• The practical use of alternative divergence measures in
common Bayesian frameworks like Stan and PyMC3 is limited
• The KL-divergence (i.e. ELBO) is still a very convenient
measure to calculate

71. 71/81
Alternative divergence measures: α-divergence
• Also called R´enyi divergence, it is a generalization of the
Kullback-Leibler divergence
• Dα(Q P) =
1
α − 1
log
Θ
q(θ)α
p(θ)α−1
dθ , for 0 < α < ∞
and α = 1
• Special cases:
• limα→1 Dα(Q P) = DKL(Q P)
• limα→0 Dα(Q P) = DKL(P Q)
• For α > 0, larger values of α enforce stronger mass-covering
properites
• In practice, large values of α lead to a very high variance if
the distribution has fat tails (Wang et al., 2018)

72. 72/81
Alternative divergence measures: f -divergence
• Generalization for DKL and Dα
• Df (Q P) =
Θ
f
q(θ)
p(θ)
p(θ)dη(θ), where η(θ) is a
reference distribution over the space Θ and f is a convex
function (Sason, 2018)
• If f (t) = t log t, then Df (Q P) = DKL(Q P)
• f can also be chosen so that Df (Q P) = Dα(Q P)
• Tail-adaptive f -divergences can help solve the problems of
α-divergences

73. 73/81
Contents
1 What is variational Bayes?
2 Divergence between distributions
3 Estimating variational approximations
4 Example with PyMC3
5 Evaluating variational approximations
6 Alternative distance measures
7 Summary

74. 74/81
Summary
• The idea of variational inference is to find a probability
distribution that minimizes the divergence to the posterior
• The KL-divergence cannot be minimized directly, as it
depends on the intractable posterior
• Maximizing the ELBO is equivalent to minimizing the
KL-divergence

75. 75/81
Summary
• To maximize the ELBO, we have to make assumptions
• The most common assumption is the mean-field
assumption, which treats parameters as independent
• An easy, but inefficient, algorithm to maximize the ELBO is
CAVI
• By taking a subsample and then updating the data structure,
CAVI is more efficient and precise (SVI)

76. 76/81
Summary
• With CAVI and SVI, the model families we can use are
restricted and the ELBO has to be derived by hand
• Black-box variational inference solves these two problems
• PyMC3 and Stan use ADVI which is based on BBVI. They
provide mean-field and full rank alternatives
• There are alternatives to the KL-divergence, but are not
widely used in common frameworks

77. 77/81
Summary
What do I really need to know about
variational inference?

78. 78/81
Twitter: @ flaviomorelli
GitHub: @flaviomorelli
LinkedIn: Flavio Morelli
Email: flavio.morelli@fu-berlin.de

79. 79/81
Bibliography I
Blei, D. M. (2017). Variational Inference: Foundations and
Innovations. Retrieved 2019-11-30, from
https://youtu.be/Dv86zdWjJKQ
Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational
Inference: A Review for Statisticians. Journal of the
American Statistical Association, 112(518), 859–877.
Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent Dirichlet
Allocation. Journal of Machine Learning Research, 3,
993–1022.
Ioannides, A. (2018). Regression in PYMC3 using MCMC &
VariationalInference. Retrieved 2019-11-25, from https://
alexioannides.com/2018/11/07/bayesian-regression
-in-pymc3-using-mcmc-variational-inference

80. 80/81
Bibliography II
Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., & Blei,
D. M. (2017). Automatic Differentiation Variational
Inference. Journal of Machine Learning Research, 18(14),
1–45.
Minka, T. (2005). Divergence measures and message passing
(Tech. Rep. No. MSR-TR-2005-173). Microsoft Research.
Ormerod, J. T., & Wand, M. P. (2010). Explaining Variational
Approximations. The American Statistician, 64(2), 140–153.
Ranganath, R., Gerrish, S., & Blei, D. M. (2014). Black Box
Variational Inference. In Proceedings of Artificial Intelligence
and Statistics.
Robbins, H., & Monro, S. (1951). A Stochastic Approximation
Method. The Annals of Mathematical Statistics, 22(3),
400–407.
Sason, I. (2018). On f-Divergences: Integral Representations,
Local Behavior, and Inequalities. Entropy, 20(5), 383.

81. 81/81
Bibliography III
Sia, X. Y. S. (2019). Coordinate Ascent Mean-field Variational
Inference (Univariate Gaussian Example). Retrieved
2019-11-20, from https://suzyahyah.github.io/
bayesian%20inference/machine%20learning/
variational%20inference/2019/03/20/CAVI.html
Wang, D., Liu, H., & Liu, Q. (2018). Variational Inference with
Tail-adaptive f-Divergence. In Advances in Neural
Information Processing Systems.
Yao, Y., Vehtari, A., Simpson, D., & Gelman, A. (2018). Yes, but
Did It Work?: Evaluating Variational Inference. In
Proceedings of the 35th International Conference on
Machine Learning.