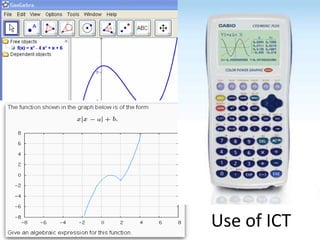
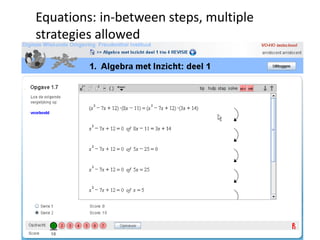
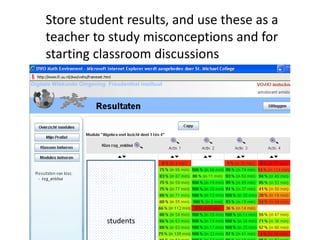
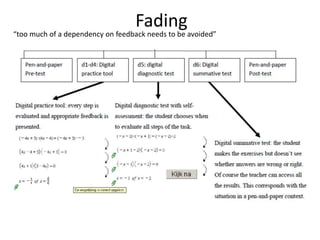
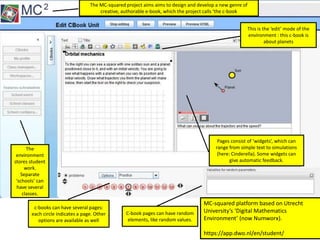
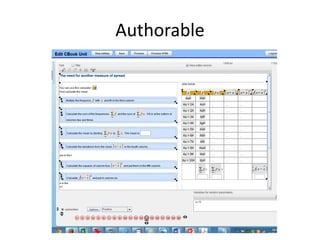
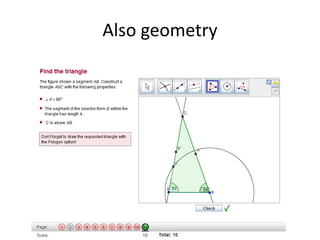
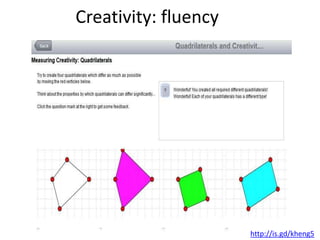
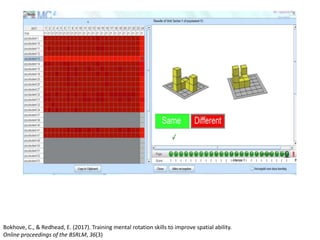
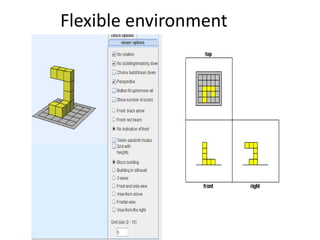
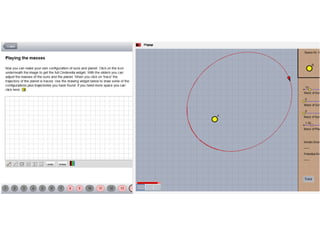
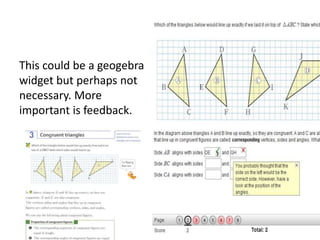
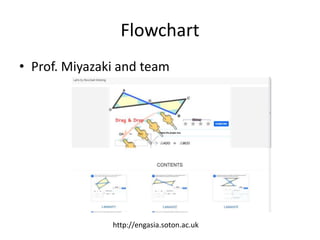
The document discusses the use of technology in mathematics education, focusing on various projects and methodologies employed by Dr. Christian Bokhove and the Freudenthal Institute. It highlights the importance of creating interactive digital learning environments, implementing effective feedback mechanisms, and promoting conceptual understanding through realistic contexts and guided reinvention. Furthermore, it touches on ongoing projects, including the Engasia project, aimed at enhancing geometry education across different countries.

1. Using technology to
support mathematics
education and research
Dr. Christian Bokhove
13 July 2017
Hong Kong

2. Who am I
• Dr. Christian Bokhove
• From 1998-2012 teacher maths, computer science, head of
ICT secondary school Netherlands
• National projects Maths & ICT at Freudenthal Instituut,
Utrecht University
• PhD 2011 under Prof. Jan van Maanen and prof. Paul Drijvers
• Lecturer at University of
Southampton
– Maths education
– Technology use
– Large-scale assessment
– Computer Science stuff

3. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY 
DIGITAL MATHEMATICAL BOOKS 
ENGASIA 
CONCLUSION

4. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY
DIGITAL MATHEMATICAL BOOKS
ENGASIA
CONCLUSION

5. Wisweb and WELP
• Wisweb: collections of (Java) applets
• WELP: integrate the use of the applets in lessons

6. Galois and sage projects
• Government grant
programme for
teacher innovations
• Make integrated
version
• First version of the
‘Digital Mathematics
Environment’ (Peter
Boon)
• Sage: prize money

7. More on FI
With thanks to Prof. Paul Drijvers

8. Hans Freudenthal (1905-1990)
„Mathematics as human
activity“
• construct content from
reality
• organize phenomena
with mathematical
means

9. The iceberg metaphor

10. RME Key Characteristics
• Meaningful contexts as starting
point for learning
• Progressive mathematization from
informal strategies and (horizontal
and vertical)
• Intertwinement of content strands
• Interaction
• Room for students’ own
constructions
(Treffers, 1987)

11. What do we mean by “Realistic”?
“Realistic” may have different meanings:
• Realistic in the sense of feasible in educational practice
• Realistic in the sense of related to real life
(real world, phantasy world, math world)
• Realistic in the sense of meaningful, sense making for
students
• Realistic in the sense of “zich realiseren” = to realize, to
be aware of, to imagine
• HF: “How real the concepts are depends on the
conceiver”
11

12. Key RME design heuristics
A. Guided reinvention
B. Didactical phenomenology
C. Horizontal and Vertical Mathematization
D. Emergent Modeling

13. A. Guided reinvention
• Reinvention:
Reconstructing and developing a mathematical
concept in a natural way in a given problem
situation.
• Guidance:
Students need guidance (from books, peers,
teacher) to ascertain convergence towards
common mathematical standards
• Reinvention <-> guidance: a balancing act

14. B. Didactical phenomenology
The art to find phenomena, contexts, problem
situations that …
• … beg to be organized by mathematical means
• … invites students to develop the targeted
mathematical concepts
These phenomena can come from real life or
can be ‘experientially real’

15. ‘Realistic’ context Mathematical model
Mathematical objects,
structures, methods
Horizontal mathematization
Translate
Vertical
mathematization
Abstract
C. Mathematization

16. D. Emergent modeling
• View on mathematics
education which aims at
the development of models
• Models of informal
mathematical activity
develop into models for
mathematical reasoning
• Level structure by
Gravemeijer
situational
referential
general
formal

17. Some debate
• Implementation ok? (Gravemeijer, Bruin-Muurling,
Kraemer, & van Stiphout, 2016)
• Influence of contexts? (Hickendorff, 2013)
• Procedural skills and conceptual understanding go
hand in hand (Rittle-Johnson, Schneider, & Star, 2015)
• Not enough emphasis on procedural skills e.g.
algorithms (Fan & Bokhove, 2014)
I don’t see a contradiction doing both. Combined in
subsequent PhD work

18. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY
DIGITAL MATHEMATICAL BOOKS
ENGASIA
CONCLUSION

19. Part of PhD
Algebraic skills
Year 12 students
Netherlands
often
disappointing

20. But even when rewriting
skills are OK…
…many things can go wrong

21. So conceptual understanding and
pattern recognition are important!

22. Use of ICT

23. So can’t we use ICT for acquiring,
practicing and assessing algebraic
expertise?

24. Equations: in-between steps, multiple
strategies allowed

25. Store student results, and use these as a
teacher to study misconceptions and for
starting classroom discussions
students

26. Design principles
(i) students learn a lot from what goes wrong,
(ii) but students will not always overcome these if
no feedback is provided, and
(iii) that too much of a dependency on feedback
needs to be avoided, as summative assessment
typically does not provide feedback.
These three challenges are addressed by principles
for crises, feedback and fading, respectively.

27. Crisis-tasks
“students learn a lot from what goes wrong”

28. Feedback: worked examples and hints
IDEAS feedback, webservice with Jeuring et al

29. Fading
“too much of a dependency on feedback needs to be avoided”

30. Hands-on: Equations
http://is.gd/hkeng1
These are HTML5 versions of those applets.

31. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY
DIGITAL MATHEMATICAL BOOKS
ENGASIA
CONCLUSION

32. Towards digital textbooks
• Digital textbook: theory, examples,
explanations
• Interactive content (in MC-squared widgets)
• Interactive quizzes (formative assessment,
feedback)
• Integrated workbook

33. FP7 EU project
Designing creative electronic books
for mathematical creativity

34. The
environment
stores student
work.
Separate
‘schools’ can
have several
classes.
This is the ‘edit’ mode of the
environment : this c-book is
about planets
c-books can have several pages:
each circle indicates a page. Other
options are available as well
C-book pages can have random
elements, like random values.
Pages consist of ‘widgets’, which can
range from simple text to simulations
(here: Cinderella). Some widgets can
give automatic feedback.
The MC-squared project aims aims to design and develop a new genre of
creative, authorable e-book, which the project calls 'the c-book
MC-squared platform based on Utrecht
University’s ‘Digital Mathematics
Environment’ (now Numworx).
https://app.dwo.nl/en/student/

35. Authorable

36. Feedback

37. Also geometry

38. Creativity: fluency
http://is.gd/kheng5

39. Bokhove, C., & Redhead, E. (2017). Training mental rotation skills to improve spatial ability.
Online proceedings of the BSRLM, 36(3)

40. Flexible environment

42. Hands-on: Cube Buildings
http://is.gd/hkeng2: Cube Buildings
http://is.gd/hkeng3: Planets
These are HTML5 versions of those applets.

43. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY
DIGITAL MATHEMATICAL BOOKS
ENGASIA
CONCLUSION

44. enGasia project
1. Compare geometry education in England, Japan and
Hong Kong → some shown now.
2. two digital resources (electronic books) will be
designed. They are then implemented in classrooms
in those countries.
3. The methodology will include a more qualitative
approach based on lesson observations and a quasi-
experimental element.

45. This could be a geogebra
widget but perhaps not
necessary. More
important is feedback.

46. Challenges
• Differences in curriculum regarding geometry
• School and teacher participation
• Software: Java
Now writing the findings in several articles.

47. Flowchart
• Prof. Miyazaki and team
http://engasia.soton.ac.uk

48. Contents
WORKING WITH THE FREUDENTHAL INSTITUTE
ALGEBRA AND TECHNOLOGY
DIGITAL MATHEMATICAL BOOKS
ENGASIA
CONCLUSION

49. Technology-added value of the c-books
• Creative and interactive activities made by designers (creative
process authoring)
• Collaboration within CoI between designers, teachers and
computer scientists. Feeds into DA component (see later
section)
• Interactivity: feedback design
• More than one widget factories used
• All student data stored
• Sum is more than the parts…
Bokhove, C., (in press). Using technology for digital maths textbooks: More than the sum of the parts.
International Journal for Technology in Mathematics Education.

50. Thank you
• Contact:
–C.Bokhove@soton.ac.uk
–Twitter: @cbokhove
–www.bokhove.net
• Most papers available somewhere; if
can’t get access just ask.
• I’ll add the references and post on
Slideshare

51. Bokhove, C., (in press). Using technology for digital maths textbooks: More than the sum of the parts. International
Journal for Technology in Mathematics Education.
Bokhove, C., &Drijvers, P. (2010). Digital tools for algebra education: criteria and evaluation. International Journal of
Computers for Mathematical Learning, 15(1), 45-62. Online first.
Bokhove, C., & Drijvers, P. (2012). Effects of a digital intervention on the development of algebraic expertise.
Computers & Education, 58(1), 197-208. doi:10.1016/j.compedu.2011.08.010
Bokhove, C., & Redhead, E. (2017). Training mental rotation skills to improve spatial ability. Online proceedings of
the BSRLM, 36(3)
Fan, L., & Bokhove, C. (2014). Rethinking the role of algorithms in school mathematics: a conceptual model with
focus on cognitive development. ZDM-International Journal on Mathematics Education, 46(3), doi:10.1007/s11858-
014-0590-2
Fischer, G. (2001). Communities of interest: learning through the interaction of multiple knowledge systems. In the
Proceedings of the 24th IRIS Conference S. Bjornestad, R. Moe, A. Morch, A. Opdahl (Eds.) (pp. 1-14). August 2001,
Ulvik, Department of Information Science, Bergen, Norway.
Freudenthal, H. (1991). Revisiting Mathematics Education. China Lectures. Dordrecht: Kluwer Academic Publishers.
Gravemeijer, K., Bruin-Muurling, G., Kraemer, J-M. & van Stiphout, I. (2016). Shortcomings of mathematics
education reform in the Netherlands: A paradigm case?, Mathematical Thinking and Learning, 18(1), 25-44,
doi:10.1080/10986065.2016.1107821
Hickendorff M. (2013), The effects of presenting multidigit mathematics problems in a realistic context on sixth
graders' problem solving, Cognition and Instruction 31(3), 314-344.
Jaworksi, B. (2006). Theory and practice in mathematics teaching development: critical inquiry as a mode of
learning in teaching. Journal of Mathematics Teacher Education, 9(2), 187-211.
Rittle-Johnson, B. Schneider, M. & Star, J. (2015). Not a one-way street: Bi-directional relations between procedural
and conceptual knowledge of mathematics. Educational Psychology Review, 27. doi:10.1007/s10648-015-9302-x
Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction – The
Wiskobas project. Dordrecht: D. Reidel Publishing Company.
Wenger, E. (1998). Communities of Practice: Learning, Meaning, Identity. Cambridge University Press.