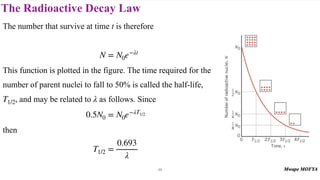
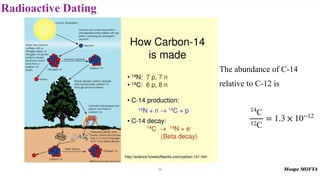
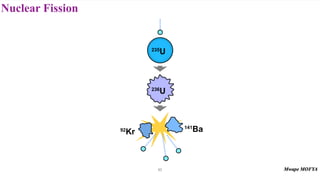
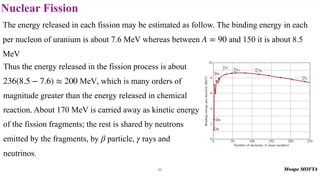
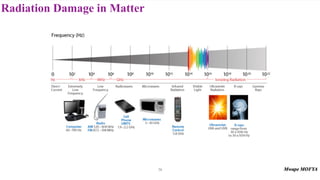
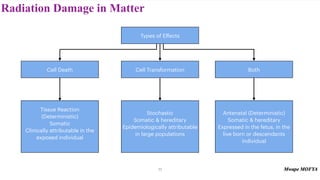
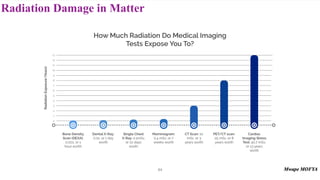
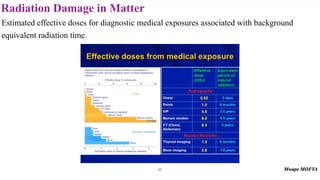
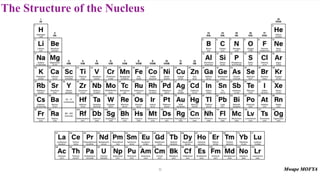
This document provides an introduction to nuclear physics and radioactivity. It discusses: 1) The discovery of radioactivity and the nucleus. Rutherford's scattering experiment in 1911 revealed the existence of the nucleus as the source of radioactivity. 2) The structure of the nucleus, including its composition of protons and neutrons (nucleons), atomic number, mass number, isotopes, and typical size. 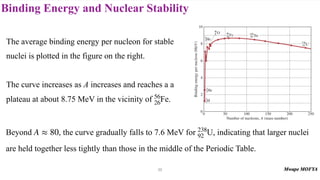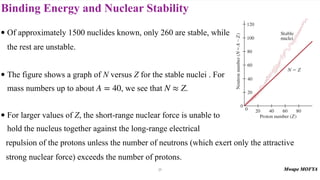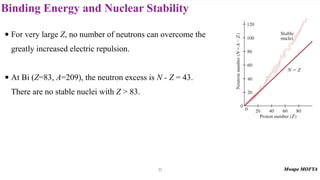3) Nuclear stability and binding energy. The strong nuclear force holds nuclei together, and nuclei with intermediate mass numbers have the highest binding energy per nucleon. Only certain combinations of protons and neutrons produce stable nuclei.

1. Introduction to Nuclear Physics and
Radioactivity
1

2. Lect-1
After this lecture, you should be able to:
1. Discovering the nucleus. Recall the general arrangement for Rutherford scattering and
what was learned from it.
2. Identify nuclides, atomic number (or proton number), neutron number, mass number,
nucleon, isotope, isotone, isobar, and explain the symbols used for nuclei (such as ).
3. Compute the mean radius of an atomic nucleus.
A
ZX
2

3. Introduction
• X-rays were discovered in 1895 by Wilhelm Conrad Roentgen.
• The discovery of X-rays triggered the discovery of radioactivity by Antoine Henri
Becquerel in 1896 who was the first person to discover evidence of radioactivity.
3

4. Introduction
• Late in 1897, Marie Curie discovered that thorium was also radioactive (a term she
coined). It was clear that radioactivity was produced by some unknown processes within
single atoms and was not the result of interaction between atoms.
• In 1911, when Rutherford’s scattering experiment revealed the existence of the nucleus,
he identified it as the source of radioactivity.
4

5. The Structure of the Nucleus
• The nucleus is made up of protons and neutrons which are collectively referred to as
nucleons.
• The atomic number Z, which uniquely specifies an element, is the number of protons in the
nucleus. There are 118 elements currently on the periodic table. The naturally occurring
elements from Z = 1 (hydrogen) to Z = 92 (uranium), whereas elements with Z up to 107
have been briefly created by artificial means in laboratories and nuclear accelerators.
• The atomic mass number, A = N+Z, is the total number of nucleons in a nucleus. A nucleus
with a given number of protons and neutrons is called a nuclide and is denoted by where
X is the chemical symbol.
A
ZX
5

6. The Structure of the Nucleus
• The isotopes of a given element are atoms whose nuclei have the same number of protons
but different number of neutrons. For example, naturally occurring carbon consists of 98.9%
and 1.1% .
• Isotones are nuclides of equal neutron number but different proton numbers.
• Isobars are a set of nuclides with equal mass number A, but different atomic number.
12
6C 13
6C
6

7. The Structure of the Nucleus
• The masses of atoms are nearly integer multiples of the mass of the hydrogen atom. This is
because the mass of an electron is very small compared to that of a proton, and the mass of
the neutron is approximately the same as that of the proton.
• Thus the atomic mass number, A, is approximately equal to the mass of an atom expressed
as multiples of the proton mass.
7

8. The Structure of the Nucleus
• Atomic masses are specified in terms of the unified mass unit (u). The mass of a neutral
atom of the carbon isotope atomic is defined to be exactly 12 u.
• The unified mass unit can be expressed in terms of its energy equivalent.
From the equation , the energy equivalent of 1 u is
Thus,
1 u = 931.5 MeV/
12
6 C
1 u = 1.66056 × 10−27
kg
E = mc2
E = (1.66056 × 10−27
kg) × (2.9979 × 108
m/s) = 1.4924 × 10−9
J = 931.5 MeV
c2
8

9. The Structure of the Nucleus
The masses of the proton, the neutron, and the electron are
mp = 1.67264 × 10−27
kg = 1.007276 u = 938.28 MeV/c2
mn = 1.6750 × 10−27
kg = 1.008665 u = 939.57 MeV/c2
me = 9.109 × 10−31
kg = 0.000549 u = 0.511 MeV/c2
9

10. The Structure of the Nucleus
The atomic masses that appear in the periodic table are weighted averages over the various
isotopes of each element. For example, Cl has two isotopes with approximate masses 35 u
(75.4%) and 37 u (24.6%). Thus the atomic mass listed is 35(0.754)+37(0.246) = 35.5 u.
The mass number A of an isotope is numerically equal to the atomic mass in u rounded to the
nearest integer.
10

11. The Structure of the Nucleus
11

12. The Structure of the Nucleus
Recent experiments involving the scattering electrons, protons, and neutrons indicate that
many nuclei are approximately spherical and that the radius R is approximately related to the
mass number by
fm
were 1 fermi (fm) = 10-15 m.
R ≈ 1.2A1/3
12

13. Lect-2
After this lecture, you should be able to:
1. Identify the force that holds nucleons together;
2. Compute the binding energy and the binding energy per nucleon of a nuclide;
3. Sketch a graph of the binding energy per nucleon versus mass number, indicating the
nuclei that are the most tightly bound.
4. Sketch a graph of proton number versus neutron number and identify the approximate
location of the stable nuclei, the proton-rich nuclei, and the neutron-rich nuclei.
13

14. Binding Energy and Nuclear Stability
• We might not expect a collection of protons and neutrons to come together spontaneously,
since protons are all positively charged and thus exert repulsive electric forces on each
other.
• Since stable nuclei DO stay together, what holds these nuclei together? There must exist
another force stronger that the electric repulsive force. This force is called the strong
nuclear force.
14

15. Binding Energy and Nuclear Stability
• The strong nuclear force turns out to be far more complicated than the gravitational and
electromagnetic forces. One important aspect of the strong nuclear force is that it is a short-
range force: it acts only over a very short distance ( fm).
• An important feature of the strong nuclear force is that it is essentially the same for all
nucleons, independent of charge.
< 2
15

16. Binding Energy and Nuclear Stability
• The binding energy (BE) of a nucleus is the energy required to completely separate the
nucleons.
• The origin of the binding energy may be understood with the help of the mass-energy
relation,
,
where is the difference between the total mass of the separated nucleons and the mass
of the stable nucleus.
ΔE = Δmc2
Δm
16

17. Binding Energy and Nuclear Stability
• The mass of the stable nucleus is less than the sum of the masses of its nucleons. This
difference is called the mass deficit, or sometimes the mass defect.
• Let M be the mass of a nucleus and m the mass of the individual nucleons. M is less than the
total mass m of its individual protons and neutrons. That means that the mass energy Mc2
of a nucleus is less than the total mass energy (mc2) of its individual protons and neutrons.
The binding energy BE of the nucleus is can be written as
Σ
Σ
BE = Σmc2
− Mc2
= (Σm − M)c2
17

18. Binding Energy and Nuclear Stability
• Since it is easier to get the masses of neutral atoms from tables, the binding energy of a
nuclide is can be found from the expression
• The quantities mH and mX are the masses of neutral atoms, because it is these atoms that are
listed in tables and the masses of electrons in ZmH and mX cancel.
A
ZX
BE = [ZmH + Nmn − mX]c2
18

19. Example 1
What is the binding energy of the helium nucleus, ?
BE = 28.3 MeV
The average binding energy per nucleon is BE/A = 28.3 MeV/4 = 7.1 eV
4
2He
BE = [ZmH + Nmn − mX]c2
BE = [(2 × 1.007825) + (2 × 1.008665) − (4.002604)]c2
19

20. Binding Energy and Nuclear Stability
The average binding energy per nucleon for stable
nuclei is plotted in the figure on the right.
The curve increases as A increases and reaches a a
plateau at about 8.75 MeV in the vicinity of .
56
26Fe
20
Beyond , the curve gradually falls to 7.6 MeV for , indicating that larger nuclei
are held together less tightly than those in the middle of the Periodic Table.
A ≈ 80 238
92 U

21. Binding Energy and Nuclear Stability
• Of approximately 1500 nuclides known, only 260 are stable, while
the rest are unstable.
• The figure shows a graph of N versus Z for the stable nuclei . For
mass numbers up to about , we see that .
• For larger values of Z, the short-range nuclear force is unable to
hold the nucleus together against the long-range electrical
A = 40 N ≈ Z
21
repulsion of the protons unless the number of neutrons (which exert only the attractive
strong nuclear force) exceeds the number of protons.

22. Binding Energy and Nuclear Stability
22
• For very large Z, no number of neutrons can overcome the
greatly increased electric repulsion.
• At Bi (Z=83, A=209), the neutron excess is N - Z = 43.
There are no stable nuclei with Z > 83.

23. Binding Energy and Nuclear Stability
• A stable nucleus is one that stays together indefinitely. An unstable nucleus is one that
comes apart; and this results in radioactive decay.
• There is a second type of nuclear force that is much weaker than the strong nuclear force. It
is called the weak nuclear force (or just weak force, or weak interaction). The weak
force acts inside of individual nucleons, which means that it is even shorter ranged than the
strong force. It is the force that allows protons to turn into neutrons and vice versa through
beta decay.
• The strong nuclear force, the weak nuclear force, the gravitational force and the
electromagnetic force comprise the four fundamental types of force in nature.
23

24. Lect-3
After this lecture, you should be able to:
1. Identify the two types of beta particles and the two types of beta decay. Explain why the
beta particles in beta decays are emitted with a range of energies. For a given beta decay,
calculate the mass change and the Q of the reaction. Determine the change in the atomic
number Z of a nucleus undergoing a beta decay and identify that the mass number A does
not change. Identify neutrino.
2. Identify that the atomic number Z and the mass number A of a nucleus undergoing a
gamma decay does not change.
3. For a given alpha decay, calculate the mass change and the Q of the reaction. Determine
the change in atomic number Z and mass number A of a nucleus undergoing alpha decay.
24

25. Radioactivity
The radioactive decays of various unstable isotopes can produce
• -rays (Helium nuclei, with charge +2e, decay);
• - rays (negative electrons, with charge -e, - decay);
• + rays (positive electrons or "positrons", with charge +e, + decay); and
• electromagnetic radiation ( rays or X rays, according to the frequency interval
and/or the radiation origin - nuclear or atomic).
α α
β β
β β
γ
25

26. Radioactivity
In general the charged particles ( and ) have a very short path in media. In particular, the
cannot be used to produce images because they cannot cross tissues to be detected.
If as an example we refer to water one has that:
- an -ray of 5 MeV has a range of only 0.01 cm in water (roughly its range in air is 1
cm/MeV); in general, the range of particles in organic tissues is less than 0.01 cm:
less than the dead layer of the skin;
- electrons and positrons of 1 MeV have in water a range of 0.4 cm;
- rays of 1 MeV have in water a range of several cm.
α β
α
α
γ
26

27. Radioactivity
27
A pictorial representation of these properties is shown in the picture; the absorption of ,
and rays in the first layers of the skin is shown (typically the epidermis has a thickness of a
few tens of microns, the dermis of 2-3 mm).
rays do not even penetrate into the epidermis;
rays are stopped in the dermis;
rays can cross the subcutaneous tissue.
α β
γ
α
β
γ

28. Radioactivity
28
Since the and rays are totally absorbed at distances that are very short in
comparison with the dimensions of the human body, they cannot cross the human body
and therefore they cannot produce images, which can instead only be obtained using
electromagnetic radiation.
α β

29. Decay
β−
29
The negative beta decay ( - ) consists in the emission of negative electrons, accompanied by
antineutrinos, with at the same time a transformation inside the nucleus of a neutron into a
proton (the electric charge Z of the nucleus increases by one unit, while A remains constant).
In general, this decay takes place in the neutron-rich unstable nuclei.
β
A
ZX β−
→ A
Z+1X v̄e
+ +

30. Decay
β−
30
The general scheme is
A(Z,N) ! A(Z+1, N-1) + electron + antineutrino.
The transition conserves the total number of nucleons (A = Z +N), while the value of Z
increases by one unit, the value of N decreases by one unit.
The simplest - decay is the neutron decay:
n ! p + electron + antineutrino.
β

31. Decay
β−
31
The energy released in any decay event is called the disintegration energy, Q. The “Q-value"
is given by
Q = m(A,Z,N) c2 – m(A,Z+1,N-1) c2
Q-value is shared between the electron and the antineutrino.

32. Decay
β+
32
The positive beta decay ( +) consists in the emission of positrons (positive electrons),
accompanied by neutrinos, with at the same time a transformation inside the nucleus of a
proton into a neutron (the electric charge Z of the nucleus decreases by one unit; again the
value of A remains constant).
In general, the positive beta decay takes place in the proton-rich unstable nuclei.
β
A
ZX β+
→ A
Z−1X ve
+ +

33. Decay
β+
33
The Q-value (available kinetic energy) for the + decay is given by the nuclear transition
energy minus the quantity 2mec2 (1022 KeV; where me is the electron – and positron – mass,
mec2 = 511 keV):
Q = m(A,Z,N) c2 – m(A,Z -1,N + 1) c2 – 2mec2
β

34. Example 2
34
How much energy is released when C (atomic mass = 14.003242 u) decays to N (atomic
mass = 14.003074 u) by emission?
Q = m(A,Z,N) c2 – m(A,Z+1,N-1) c2
MeV
14
6
14
7
β
Q = (14.003242 − 14.003071)c2
= 0.156

35. Decay
γ
35
Often a decay (both the and the + ) does not lead to the ground state of the daughter
nucleus, but to one or more of the daughter excited levels; this excited level will afterwards
decay to a lower energy level (to the ground state, or to another excited level), in general
emitting radiation.
β β β
γ
The gamma decay ( ) consists of the emission of electromagnetic radiation in a transition
from an excited nuclear level to the ground state (or to another excited level, whose energy is
lower than the one of the initial level).
γ

36. Decay
γ
36
In a gamma decay, the value of A remains constant.

37. Decay
α
37
The alpha decay ( ) consists in the emission of a Helium nucleus, ( particle is synonymous
of a Helium nucleus) with a reduction of the values of A and Z of the parent nucleus (from A, Z
to A - 4 and Z - 2).
α α

38. Decay
α
38
An example of decay, the decay of 220Rn86 (Radon) into 216Po84 (Polonium) is shown in the
figure. The decay can end either in an excited state of the Polonium or in its ground state, and
therefore two lines are emitted, with two different energies.
α
α
For decay, the Q value is given by
Q = m(A,Z,N) c2 – m(A,Z-2,N-2) c2 - mHe c2
α

39. Why decay?
α
39
Why, you may wonder, do nuclei emit this combination of four nucleons called an particle?
Why not just four separate nucleons, or even one?
The answer is that the particle is very strongly bound, so that its mass is significantly less
than that of four separate nucleons. That helps the final state in a decay to have less total mass,
thus allowing certain nuclides to decay which could not decay to, say, 2 protons plus 2
neutrons.
α
α

40. Why decay?
α
40
For example, U could not decay to 2p + 2n because the masses of the daughter Th plus
four separate nucleons is 228.028741 u + 2(1.007825 u) + 2(1.008665 u) = 232.061721 u,
which is greater than the mass of the U parent (232.037156 u).
Such a decay would violate the conservation of energy.
232
92
228
90
232
92

41. Lect-4
After this lecture, you should be able to:
1. Explain what is meant by radioactive decay and identify that it is a random process.
2. Identify disintegration constant (or decay constant) .
3. Identify that, at any given instant, the rate dN/dt at which radioactive nuclei decay is
proportional to the number N of them still present then.
4. Apply the relationship that gives the number N of radioactive nuclei as a function of time.
Apply the relationship that gives the decay rate A of radioactive nuclei as a function of
time.
5. Identify that in any nuclear process, including radioactive decay, the charge and the
number of nucleons are conserved.
6. Explain how radiocarbon dating can be used to date the age of biological samples.
λ
41

42. The Radioactive Decay Law
42
Radioactive decay is a random process: Each decay is an independent event, and one cannot
tell when a particular nucleus will decay.
When a given nucleus decays, it is transformed into another nuclide, which may or may not be
radioactive.

43. The Radioactive Decay Law
43
Since radioactive decay is a spontaneous and random process, any radioactive nucleus may
decay at any moment. For each second that it exists, there is a certain probability that the
nucleus will decay. This probability is what is called the decay constant.
Just like guessing which number will come up next in a lottery, it is not possible to predict
when any given nucleus will decay.
The likelihood that a particular nucleus will decay is not affected by factors outside of the
nucleus, such as temperature of pressure or the behavior of the neighboring nuclei. Each
nucleus acts entirely independently.

44. The Radioactive Decay Law
44
When there is a very large number of nuclei in a sample, the rate of decay is proportional to
the number of nuclei, N, that are present:
where is called the decay constant. The minus sign in this formula occurs because the
number of nuclei in the sample, N, decreases with time.
dN
dt
= − λN
λ

45. The Radioactive Decay Law
45
The formula for the rate of decay may be expressed as
and integrated
to yield
were is the initial number of the parent nuclei at t = 0.
dN
N
= − λdt
∫
N
N0
dN
N
= − λ
∫
t
0
dt
ln
N
N0
= − λt
N0

46. The Radioactive Decay Law
46
The number that survive at time t is therefore
This function is plotted in the figure. The time required for the
number of parent nuclei to fall to 50% is called the half-life,
, and may be related to as follows. Since
then
N = N0e−λt
T1/2 λ
0.5N0 = N0e−λT1/2
T1/2 =
0.693
λ

47. The Radioactive Decay Law
47
The number of decays per second, or decay rate A, is the magnitude of , and is also
called the activity of the sample.
were is the initial decay rate.
dN/dt
A =
dN
dt
= λN = λN0e−λt
= A0e−λt
A0 = λN0

48. The Radioactive Decay Law
48
The SI unit for activity is the becquerel (Bq), named after Antoine Becquerel (1852–1908).
One becquerel equals one disintegration per second. Activity is also measured in terms of a
unit called the curie (Ci), in honor of Marie (1867–1934) and Pierre (1859–1906) Curie, the
discoverers of radium and polonium.
Historically, the curie was chosen as a unit because it is roughly the activity of one gram of
pure radium. In terms of becquerels,
1 Ci = Bq
3.7 × 1010

49. Example 3
49
The isotope C has a half-life of 5730 yr. If a sample contains carbon-14 nuclei,
what is the activity of the sample?
s-1
decays/s
14
6 1.00 × 1022
T1/2 =
ln 2
λ
λ =
ln 2
T1/2
=
ln 2
1.807 × 1011
= 3.836 × 10−12
A = λN = 3.836 × 10−12
× 1.00 × 1022
= 3.836 × 1010

50. Example 4
50
What is the initial decay rate of 1 g of radium 226? Its half-life is 1620 y and its molecular
mass M = 226 g/mol.
; atoms
s-1
decays/s = 0.97 Ci
n =
m
M
n =
N
NA
m
M
=
N
NA
N =
mNA
M
=
1 × 6.02 × 1023
226
= 2.66 × 1021
λ =
ln 2
T1/2
=
ln 2
5.109 × 1010
= 1.357 × 10−11
A = λN = 1.357 × 10−11
× 2.66 × 1021
= 3.61 × 1010

51. Radioactive Dating
51
The abundance of C-14
relative to C-12 is
14
C
12C
= 1.3 × 10−12

52. Lect-5
After this lecture, you should be able to:
1. Define a nuclear reaction. Explain the difference between an endothermic reaction and an
exothermic reaction.
2. Define the fission process. Define the fusion process. Explain why nuclei must be at a
high temperature to fuse.
3. For a given fission process, calculate the Q value in terms of the binding energy per
nucleon.
4. Identify the approximate amount of energy (MeV) in the fission of any high-mass nucleus
to two middle-mass nuclei.
52

53. Nuclear Reactions
53
It is also possible to induce the disintegration of a stable nucleus by striking it with another
nucleus, an atomic or subatomic particle, or a -ray photon.
A nuclear reaction is said to occur whenever an incident nucleus, particle, or photon causes a
change to occur in a target nucleus.
γ

54. Nuclear Reactions
54
In 1919, Ernest Rutherford observed that when an particle strikes a nitrogen nucleus, an
oxygen nucleus and a proton are produced. This nuclear reaction is written as
This was the first artificially induced transmutation of one element into another.
α
4
2α +14
7 N →17
8 O +1
1 p

55. Nuclear Reactions
55
Since then, much information about nuclei has been obtained by bombarding them with
particles such as protons, neutrons, electrons and alpha particles.
A nuclear reaction in which a collision between particle a and nucleus X produces nucleus Y
and particle b is represented as
a + X Y + b
→

56. Nuclear Reactions
56
This reaction is sometimes expressed in the shorthand notation
X (a, b) Y
The symbols outside the parentheses on the left and right represent the initial and final nuclei,
respectively. The symbols inside the parentheses represent the bombarding particle (first) and
the emitted small particle (second).

57. Nuclear Reactions
57
The reaction energy, Q, is determined by the mass difference between the initial set of
particles and the final set:
were the masses are of the neutral atoms.
If energy is released by the reaction, Q > 0 and the reaction is said to be exothermic. The
energy released generally goes into kinetic energy of the products and rays due to transitions
between excited states of Y.
Q = Δmc2
= (ma + mX − mY − mb)c2
γ

58. Nuclear Reactions
58
If energy is required, Q < 0 and the reaction is said to be endothermic: an energy input is
required to make the reaction happen. The energy input comes from the kinetic energy of the
initial colliding particles (a and X).
The special case Q = 0 corresponds to elastic scattering, denoted by X(a, a)X. Although a and
X might exchange energy, the total kinetic energy does not change.

59. Nuclear Fission
59
Nuclear fission is the process that occurs in present-day nuclear reactors and ultimately results
in energy supplied to a community by electrical transmission.
To understand nuclear fission and the physics of nuclear reactors, we must first understand
how neutrons interact with nuclei.
Because neutrons have no charge, they are not subject to Coulomb forces and as a result do
not interact electrically with electrons or the nucleus. Therefore, neutrons can easily penetrate
deep into an atom and collide with the nucleus, inducing artificial radioactivity more easily
than protons or particles.
α

60. Nuclear Fission
60
Thermal neutrons have a a high probability of being captured by a nucleus, an event that is
accompanied by the emission of a gamma ray.
This neutron capture reaction can be written
Once the neutron is captured, the nucleus is in an excited state for a very short time
before it undergoes gamma decay. The product nucleus is usually radioactive and decays
by beta emission.
1
0n +A
Z X →A+1
Z X*
→A+1
Z X + γ
A+1
Z X*
A+1
Z X

61. Nuclear Fission
61
Nuclear fission is a process in which the nucleus of an atom splits into two or more smaller
nuclei as fission products, and usually some by-product particles. Hence, fission is a form of
elemental transmutation.
Fission is initiated when a heavy nucleus captures a thermal neutron.The absorption of the
neutron creates a nucleus that is unstable and can change to a lower-energy configuration by
splitting into two smaller nuclei.
The by-products include free neutrons, photons usually in the form rays, and other nuclear
fragments such as beta particles and particles.
γ
α

62. Nuclear Fission
62

63. Nuclear Fission
63
The fission of by thermal neutrons can be represented by the reaction
where is an intermediate excited state that lasts for approximately s before
splitting into medium-mass nuclei X and Y, which are called fission fragments.
235
92U
1
0n +235
92 U →236
92 U*
→ X + Y + neutrons
236
92U*
10−12

64. Nuclear Fission
64
Fission also results in the production of several neutrons, typically two
or three. On average, approximately 2.5 neutrons are released per event.
A typical fission reaction for uranium is
1
0n +235
92 U →141
56 Ba +92
36 Kr + 3(1
0n)

65. Nuclear Fission
65
The energy released in each fission may be estimated as follow. The binding energy in each
per nucleon of uranium is about 7.6 MeV whereas between and 150 it is about 8.5
MeV
A = 90
Thus the energy released in the fission process is about
, which is many orders of
magnitude greater than the energy released in chemical
reaction. About 170 MeV is carried away as kinetic energy
of the fission fragments; the rest is shared by neutrons
emitted by the fragments, by particle, rays and
neutrinos.
236(8.5 − 7.6) ≈ 200 MeV
β γ

66. Nuclear Fission
66
The neutrons released in one fission event may be used to induce fissions in other nuclei.
Under suitable conditions, the process can repeat itself, thereby setting up a chain reaction.
The energy release is uncontrolled (i.e., the chain reaction does not proceed slowly) in an
atomic bomb.When the reaction is controlled, however, the energy released can be put to
constructive use. In the United States, for example, nearly 20% of the electricity generated
each year comes from nuclear power plants, and nuclear power is used extensively in many
other countries, including France, Japan, and Germany.

67. Nuclear Fusion
67
• Nuclear fusion is an area of active research, but it has not yet been commercially developed
for the supply of energy.
• Nuclear fusion is a reaction in which two or more atomic nuclei are combined to form one
or more different atomic nuclei and subatomic particles (neutrons or protons).
• The difference in mass between the reactants and products is manifested as either the
release or the absorption of energy. This difference in mass arises due to the difference in
atomic binding energy between the nuclei before and after the reaction.

68. Nuclear Fusion
68
• A fusion process that produces nuclei lighter than iron-56 or nickel-62 will generally
release energy. These elements have relatively small mass per nucleon and large binding
energy per nucleon.
• Fusion of nuclei lighter than iron-56 or nickel-62 releases energy (an exothermic process),
while fusion of heavier nuclei results in energy retained by the product nucleons, and the
resulting reaction is endothermic.
• The opposite is true for the reverse process, nuclear fission. This means that the lighter
elements, such as hydrogen and helium, are in general more fusible; while the heavier
elements, such as uranium, thorium and plutonium, are more fissionable.

69. Nuclear Fusion
69
Fusion is the process that powers active or main sequence stars and other high-magnitude
stars, where large amounts of energy are released. The extreme astrophysical event of a
supernova can produce enough energy to fuse nuclei into elements heavier than iron.

70. Lect-6
After this lecture, you should be able to:
1. Identify absorbed dose, dose equivalent, and the associated units.
2. Calculate absorbed dose and dose equivalent.
3. Explain the effects of nuclear radiation passing through matter, particularly biological
matter, and how radiation is used medically for therapy, diagnosis, and imaging
techniques.
70

71. Radiation Damage in Matter
71
• Electromagnetic radiation is all around us in the form of radio waves, microwaves, light
waves, and so on.
• We now describe forms of radiation that can cause severe damage as they pass through
matter, such as radiation resulting from radioactive processes and radiation in the form of
energetic particles such as neutrons and protons.
• Ionizing radiation consists of particles, including photons, that have sufficient energy to
knock an electron out of an atom or molecule, thus forming an ion. An energy of roughly 1
to 35 eV is needed to ionize an atom or molecule.

72. Radiation Damage in Matter
72
• Directly ionizing radiation consists of charged particles. Such particles include energetic
electrons (sometimes called negatrons), positrons, protons, alpha particles, charged mesons,
muons and heavy ions (ionized atoms).
• This type of ionizing radiation interacts with matter primarily through the Coulomb force,
repelling or attracting electrons from atoms and molecules by virtue of their charges. and
particles, and rays emitted during nuclear disintegration often have energies of several
million eV. Therefore, a single particle, particle, or ray can ionize thousands of
molecules.
α
β γ
α β γ

73. Radiation Damage in Matter
73
• Indirectly ionizing radiation consists of uncharged particles such as photons and neutrons.
• The photons usually lie in the ultraviolet (UV can cause ionization under certain
circumstances), X-ray, or -ray regions of the electromagnetic spectrum.
• To distinguish these types of radiation from radiation that always causes ionization (UV can
cause ionization under certain circumstances), an arbitrary lower energy limit for ionizing
radiation usually is set around 10 keV.
γ

74. Radiation Damage in Matter
74

75. Radiation Damage in Matter
75
X-ray and gamma-ray photons interact with matter and cause ionization in at least three
different ways:
(i) Photoelectric effect
(ii) Compton effect
(iii) Pair production

76. Radiation Damage in Matter
76
• Ionizing radiation is potentially harmful to humans because the ionization it produces can
significantly alter the structure of molecules within a living cell. The alterations can lead to
the death of the cell and even of the organism itself.
• Despite the potential hazards, however, ionizing radiation is used in medicine for diagnostic
and therapeutic purposes, such as locating bone fractures and treating cancer. The hazards
can be minimized only if the fundamentals of radiation exposure, including dose units and
the biological effects of radiation, are understood.

77. Radiation Damage in Matter
77
Cell Transformation Both
Cell Death
Types of E
ff
ects
Tissue Reaction
(Deterministic)
Somatic
Clinically attributable in the
exposed individual
Stochastic
Somatic & hereditary
Epidemiologically attributable
in large populations
Antenatal (Deterministic)
Somatic & hereditary
Expressed in the fetus, in the
live born or descendants
individual

78. Radiation Damage in Matter
78
Tissue reaction (Threshold/non-stochastic)
• A large number of cells are involved
• Existence of a dose threshold value (below this dose, the effect is not observable)
• Severity of the effect increases with dose.

79. Radiation Damage in Matter
79
Stochastic
• Stochastic effects of ionising radiation induce: cancers and genetic effects
• Generally occurs with a single cell.
• For the purposes of radiation protection (conservative approach): Linear and No
Threshold model (LNT model)
- Probability of the effect increases linearly with the dose

80. Radiation Damage in Matter
80
• Everyone is continually exposed to background radiation from natural sources, such as:
- cosmic rays (high-energy particles that come from outside the solar system),
- radioactive materials in the environment,
- radioactive nuclei (primarily carbon and potassium K) within our own bodies, and
- radon.
14
6 C 40
19

81. Radiation Damage in Matter
81

82. Radiation Damage in Matter
82
An average individual dose from background radiation is estimates at approximately 1.8 mSv
per year in UK, while in USA it’s approximately 3.6 mSv. For other countries the average is
approximately 2.4 mSv per year.
To the natural background of radiation, a significant amount of human-made radiation has
been added, mostly from medical/dental diagnostic X-rays.

83. Radiation Damage in Matter
83

84. Radiation Damage in Matter
84

85. Radiation Damage in Matter
85
Estimated effective doses for diagnostic medical exposures associated with background
equivalent radiation time.

86. Radiation Damage in Matter
86
The effects of radiation on humans can be grouped into two categories, according to the time
span between initial exposure and the appearance of physiological symptoms:
(1) short-term or acute effects that appear within a matter of minutes, days, or weeks, and
(2) long-term or latent effects that appear years, decades, or even generations later.

87. Radiation Damage in Matter
87
• Radiation sickness is the general term applied to the acute effects of radiation.
• Depending on the severity of the dose, a person with radiation sickness can exhibit nausea,
vomiting, fever, diarrhea, and loss of hair. Ultimately, death can occur.
• The severity of radiation sickness is related to the dose received, and in the following
discussion the biologically equivalent doses quoted are whole-body, single doses.

88. Radiation Damage in Matter
88
- A dose less than 0.5 Sv causes no short-term ill effects.
- A dose between 0.5 and 3 Sv brings on radiation sickness, the severity increasing with
increasing dosage.
- A whole-body dose in the range of 4 - 5 Sv given within a very short period of time is
classified as an LD50/30 dose, meaning that it is a lethal dose (LD) for about 50% of the
people so exposed; death occurs within a 30 days.
- Whole-body doses greater than 6 Sv result in death for almost all individuals.

89. Radiation Damage in Matter
89
• Long-term or latent effects of radiation may appear as a result of high-level brief exposure
or low-level exposure over a long period of time.
• Some long-term effects are hair loss, eye cataracts, and various kinds of cancer.
• In addition, genetic defects caused by mutated genes may be passed on from one generation
to the next.

90. Radiation Damage in Matter
90
• Because of the hazards of radiation, governments and international organizations have
established dose limits.
• The permissible dose for an individual is defined as the dose, accumulated over a long
period of time or resulting from a single exposure, that carries negligible probability of a
severe health hazard.

91. Radiation Damage in Matter
91
Today, in all national legislations the
annual limit for the lens of the eye is
150 mSv/y
IAEA Basic Safety Standards (BSS), 2014 Dose limits for occupation exposure

92. References
92
• Giancoli, D.C., 2016. Physics: principles with applications. Pearson.
• Cutnell, J.D., 2009. Physics . John Wiley & Sons.
• Serway, R.A. and Faughn, J.S., 8th Edition. College physics. Saunders Publishers.
• Halliday, D. and Resnick, R., 2014. Fundamentals of physics. John Wiley & Sons.
• Harris, B., 1991. University Physics. John Wiley & Sons, Inc.