The document discusses number series and techniques for solving them. It explains that number series follow a fixed pattern that must be detected. Various types of patterns are described, including ones based on prime numbers, mathematical operations, using the same term, or different numbers. Examples of number series and their solutions are provided to illustrate the different patterns and approaches.

1. VERBAL REASONING
NUMBER SERIES

2. Number series
• A SERIES IS GIVEN AND WE
HAVE TO FIND THE NEXT TERM
OF THE SERIESOF THE SERIES
• THE TERMS FOLLOW A FIXED
PATTERN
• WE NEED TO DETECT THAT
PATTERN

3. •TECHNIQUE TO
SOLVE THE
NUMBER SERIESNUMBER SERIES

4. • TRY TO FIND THE PATTERN OF
THE SMALLER NUMBERS
BECAUSE THEY HAVE LESS
MAGNITUDE
• SEARCH FOR THE PATTERN
FROM THE 1,2,3,4 TERMS OF
THE SERIES IE THINK ON THE
START OF THE SERIES

5. 1, 7 , 13, 19 ,25 ?

6. •VARIOUS TYPES OF SERIES
•TYPES OF LOGIC USED TO
IDENTIFY THE VARIOUS
TYPES OF PATTERNS OFTYPES OF PATTERNS OF
THE NUMBERS OF THE
SERIES

7. TYPE -1 --------
PATTERNS BASED
ON TYPE OFON TYPE OF
NUMBERS IN THE
SERIES

8. • 1] PRIME NUMBERS
• 2] ODD NUMBERS
• 3]EVEN NUMBERS
• 4] ODD EVEN MIXED
• 5] ODD EVEN PRIME NUMBERS MIXED• 5] ODD EVEN PRIME NUMBERS MIXED
• 6] SQUARE NUMBERS
• 7] CUBE NUMBERS
• 8] NUMBERS BASED ON DIVISIBILITY LIKE
DIVISIBLE BY
2,3,4,5,6,7,8,9,11,13,17,19,23

9. • EXAMPLES
• 2,4,16,216------------------
• 1,3,5,7,9----------------
• 2,3,5,7,11,13,17,19,23------------2,3,5,7,11,13,17,19,23------------
• 2,4,3,16,5,216,7---------------
• 2,8,512-------------------
• 11,44,55,66,77,--------------

10. •TYPE -2 ----PATTERNS
BASED ON SOME
MATHEMATICAL
OPERATIONSOPERATIONS
PERFORMED ON THE
TERMS OF SERIES

11. • LET THE TERM OF THE SERIES BE
X
• SO WE WILL DENOTE THE TERM
OF THE SERIES BY X
• NOW ALL THE PATTERNS WILL• NOW ALL THE PATTERNS WILL
INVOLVE X TO GET
UNDERSTANDING OF VARIOUS
TYPES OF PATTERNS USED IN THE
NUMBER SERIES

12. • 1] ADDITION BASED
• X -------------- X + FIXED NUMBER
• 3,8------------------SERIES
• 3------------ ---3 + 5
• 2] SUBSTRACTION BASED
• X ---------------- X – FIXED NUMBER
• 28,25----------------SERIES
• 28-----------------------28 - 3

13. •3] PRODUCT BASED
•X -------------------X * FIXED
NUMBER
•25,150---------------------•25,150---------------------
SERIES
•25-------------------25*6 -------

14. • 4] division based
• X-----------------X/ FIXED NUMBER
• 152,8------------------------SERIES• 152,8------------------------SERIES
• 152-----------------------152/19

15. 5] COMBINATION OF ALL
BASIC MATHEMATICAL
OPERATIONS ON TERM
OF THE SERIESOF THE SERIES
related to fixed same
number

16. • X--------------(X + NUMBER)/NUMBER
• X--------------(X - NUMBER)/NUMBER
• X---------------(X * NUMBER) + or -
NUMBER
• X---------------(X / NUMBER ) +• X---------------(X / NUMBER ) +
NUMBER
• X---------------(X/NUMBER ) -
NUMBER

17. • EXAMPLES
• 5,12 -----------------5X2 + 2 = 12
• 6,15-----------------6x3 - 3 = 15
• 30,11----------------30/6 + 6 = 1130,11----------------30/6 + 6 = 11
• 12,5 ------------------(12+ 3)/3 = 5
• 16,7------------------(16 -2) /2 = 7

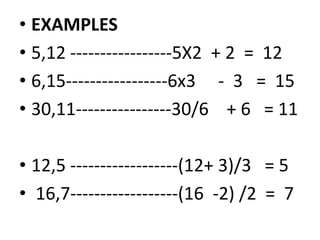
18. 6] WHEN THE MATHEMATICAL
OPERATIONS ARE PERFORMED BUT
TWO NUMBERS ARE USED IE X IS
RELATED TO 2 different numbers
NUMBER 1 AND NUMBER 2
EG --------------
X ----------------- X/NUMBER1 (+/-)X ----------------- X/NUMBER1 (+/-)
NUMBER 2
X------------------X(+/-) NUMBER1 (/)
NUMBER 2

19. • EXAMPLES -----------
• 12,64 -------------------12*5 + 4 =
64
• 11,60 -------------------11*6 - 6 =
6060
• 95,16-------------------95/5 - 3 =
16
• 68,10------------------68/17 + 6 = 10

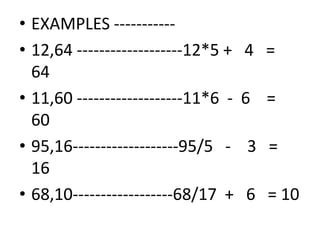
20. • 7] when then term of series is
mathematically related to a number
with a particular property like a prime
number , or square of number or a cube
of number
• Eg ----- X -------------X + PRIME NUMBER
• 15, 29 -------------------15 + 11
• 15, 40 ------------------15 + SQUARE OF 5
• 15, 6 --------------------15 - SQUARE OF 3

21. • TYPE -3 –WHEN THE SAME TERM OF THE SERIES
IS USED IN THE PATTERN
• EG ------X---------------X + (CUBE OF X)
• X---------------X - (SQUARE OF X)
• X---------------X + ( X/ Number )
• X---------------X - ( X/ Number)• X---------------X - ( X/ Number)
• X ---------------SQUARE ROOT OF X
• X ---------------CUBE ROOT OF X
• X--------------- X – (SQUARE ROOT OR CUBE
ROOT OF X)

22. • Type -4 --- When different number is
used to show the term
• Eg --------- X = ( number ) + (
number )
• Eg -----------X =( number ) + ( square
or cube of number)
• Eg -----------X = (NUMBER ) – (• Eg -----------X = (NUMBER ) – (
number)
• Eg -----------X = ( number ) – (square
or cube of number)

23. • Note -----
• X = number 1 (+/-) number 2
• X = square of number 1 (+/-)
square of number 2
• Similarly for cube, square root etc
• NUMBER 1 IS NOT EQUAL TO
NUMBER 2

24. •Combination of 2 series
•---ABCD DENOTE
NUMBERS
•A B C D E F G H I J

25. Solved examples
• Ex. 1. Which is the number that
comes next in the sequence :
0. 6. 24. 60. 120. 210 ?
Cube of 1 – 1 , cube of 2 – 2 -----Cube of 1 – 1 , cube of 2 – 2 -----
• Ans = 336 -----------cube of 7 – 7

26. • Ex. 3. Which is the number that comes next in
the following sequence ?
4, 6, 12, 14,28, 30, ( )
• a) 32 b) 60 c) 62 d) 64
4, 6. 12, 14. 28, 30. ( )SOLN ------4, 6. 12, 14. 28, 30. ( )
B
Pattern in both series = +8, +16, +32

27. Q] 1,2, 6,24, ( )
PATTERN = X 2 , X 3 ,X 4, X 5
ANS = 24 X 5 = 120
Q] 3, 12, 27, 48, 75, 108, ( )Q] 3, 12, 27, 48, 75, 108, ( )
PATTERN = 3x square of 1
= 3x square of 2
= 3x square of 3
Ans = 147

28. Q] 3. 7, 15, 31. 63. ( )
Thus. (3 x 2) + 1 = 7, (7x2) + 1 =
15,
(15x2)+l = 31 and so on.(15x2)+l = 31 and so on.
Missing number =(63 x 2) + 1 =
127.

29. Q] 66. 36, 18. ( )
Each number in the series is the
product of the digits of the
preceding number.
Thus, 6 x 6 a 36. 3 x 6 « 18 and soThus, 6 x 6 a 36. 3 x 6 « 18 and so
on.
Missing number =1x8 = 8(ANS)

30. Q] 2, 3, 8, 63, ( )
Each term in the series is one less than the
square of the preceding term.
Thus.
2(SQUARE) - 1 = 3,
3(SQUARE) - 1 = 8,3(SQUARE) - 1 = 8,
8(SQUARE) - 1 = 63.
ANS = 63(SQUARE) – 1