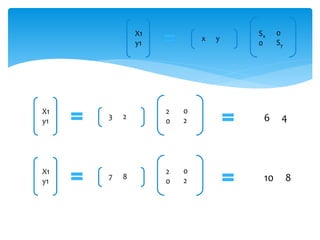
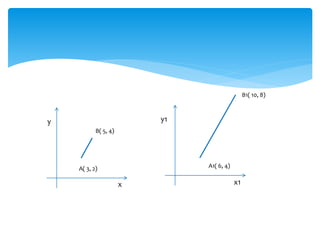
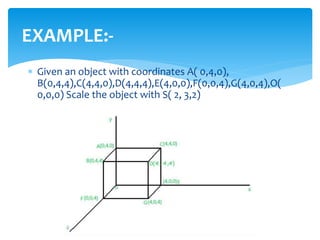
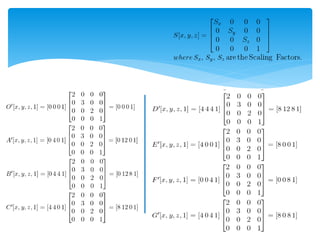
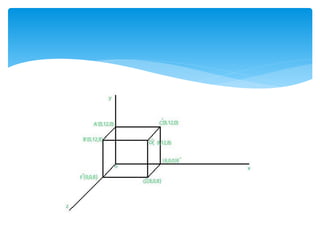
This document discusses two-dimensional and three-dimensional scaling in computer graphics. It defines scaling as modifying the size of objects by applying scaling factors to their coordinate points. Two-dimensional scaling scales objects in the x and y plane, while three-dimensional scaling also scales along the z-axis. Scaling factors above 1 increase size, below 1 decrease size, and 1 keeps the original size. Examples are given of applying scaling factors to 2D and 3D coordinate points.

1. TWO/THREE DIMENSIONAL SCALING
NAME:- ILABANTA MOHANTY
ROLL NO:- cs/02/22
CLASS:-MCA 1ST YEAR(2ND SEM)
GUIDED BY:-DR. MINATI MISHRA

2.  TRANSFORMATION
 SCALING
 TWO-DIMENSIONAL SCALING
 TWO-DIMENSIONAL SCALING FACTOR
REPRESENTATION
 THREE-DIMENSIONAL SCALING
 THREE-DIMENSIONAL SCALING FACTOR
REPRESENTATION
CONTENT:-

3.  Transformation is a process of modifying and re-
positioning the existing graphics.
 In computer graphics, various transformation
technique are-
 1)Translations
 2)Rotation
 3)Scaling
 4)Reflection
 5)Shear
TRANSFORMATION:-

4.  In computer graphics, scaling is a process of modifying
or altering the size of objects.
 Scaling may be used to increase or reduce the size of
object.
 Scaling subjects the coordinate points of the original
object to change.
 Scaling factor determines whether the object size is to
be increased or reduced.
SCALING:-

5.  If scaling factor > 1, then the object size is increased.
 If scaling factor < 1, then the object size is reduced.
 If scaling factor = 1, then the object size is same as
original size.

6. TWO DIMENSIONAL SCALING:-
 2D scaling is the change in size of the object in two
dimensional plane ( x, y).
 Size may be increase or decrease depending on
scaling factor.

7. TWO DIMESIONAL SCALING FACTOR
REPRESENTION:-
 S( SX, SY) Where ‘S’ means Scaling factor, SX means
Scaling factor for coordinate X, SY means Scaling
factor for coordinate Y.

8. EXAMPLE:-
 Given an object with coordinates A( 3, 2), B(7,8) Scale
the object with S( 2, 2)
SOLUTION:-
X1 = X . SX
= 3 . 2
= 6
Y1 = Y . SY
= 2 . 2
= 4
FOR COORDINATE A1:- FOR COORDINATE B1:-
X1 = X . SX
= 5 . 2
= 10
Y1 = Y . SY
= 4 . 2
= 8

9. X1
y1
2
0
0
2
3 2 6 4
X1
y1
2
0
0
2
7 8 10 8
X1
y1
Sx
0
0
Sy
x y

10. A( 3, 2)
x
y
x1
y1
A1( 6, 4)
B1( 10, 8)
B( 5, 4)

11. THREE DIMENSIONAL SCALING:-
 3D scaling is the change in size of the object in two
dimensional plane ( x, y, z).
 Size may be increase or decrease depending on
scaling factor.

12. THREE DIMESIONAL SCALING FACTOR
REPRESENTION:-
 S( SX, SY, SZ) Where ‘S’ means Scaling factor, SX
means Scaling factor for coordinate X, SY means
Scaling factor for coordinate Y, SZ means Scaling
factor for coordinate Z.

13. EXAMPLE:-
 Given an object with coordinates A( 0,4,0),
B(0,4,4),C(4,4,0),D(4,4,4),E(4,0,0),F(0,0,4),G(4,0,4),O(
0,0,0) Scale the object with S( 2, 3,2)

14. SOLUTION:-
X1 = X . SX
= 0 . 2
= 0
Y1 = Y . SY
= 2 . 3
= 6
Z1 = Z. SZ
= 0.2
= 0
FOR COORDINATE A1:-
X1 = X . SX
= 0 . 2
= 0
Y1 = Y . SY
= 4 . 3
= 12
Z1 = Z. SZ
= 4.2
= 8
FOR COORDINATE B1:-

15. X1 = X . SX
= 0 . 2
= 0
Y1 = Y . SY
= 0 . 3
= 4
Z1 = Z. SZ
= 4.2
= 8
X1 = X . SX
= 0 . 2
= 0
Y1 = Y . SY
= 0 . 3
= 0
Z1 = Z. SZ
= 0.2
= 0
X1 = X . SX
= 4 . 2
= 8
Y1 = Y . SY
= 4 . 3
= 12
Z1 = Z. SZ
= 0.2
= 0
X1 = X . SX
= 4 . 2
= 8
Y1 = Y . SY
= 4 . 3
= 12
Z1 = Z. SZ
= 4.2
= 8
X1 = X . SX
= 4 . 2
= 8
Y1 = Y . SY
= 0 . 3
= 0
Z1 = Z. SZ
= 0.2
= 0
X1 = X . SX
= 4 . 2
= 8
Y1 = Y . SY
= 0 . 3
= 0
Z1 = Z. SZ
= 4.2
= 8
FOR COORDINATE C1:- FOR COORDINATE D1:- FOR COORDINATE E1:-
FOR COORDINATE O1:-
FOR COORDINATE G1:-
FOR COORDINATE F1:-

18.  Website : BYJU’S.com, javapoint.com
 Youtube Channel : 5-Minute Engineering
REFERENCE:-

19. THANK YOU