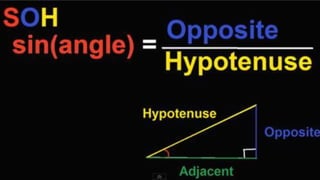
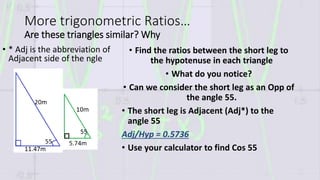
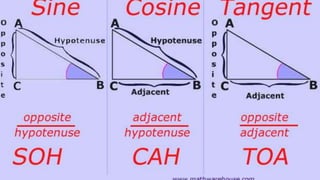
This document introduces trigonometric ratios and their use in right triangles. It discusses how similar right triangles always have equivalent ratios between corresponding sides. Specifically, it shows that the ratio of the opposite side to the hypotenuse of any angle α is equal to the sine of that angle. Similarly, the ratio of the adjacent side to the hypotenuse is equal to the cosine of the angle. The document also reviews when to use trigonometric ratios, geometric means ratios, and the Pythagorean theorem to solve for missing terms in right triangles.

1. 8.3 Trigonometry
Done by Rana Karout

2. Introduction
* Opp is abbreviation of Opposite side
of angle 40. Are these triangles similar? Why?
• Find the ratio between the short
leg (Opp*) to the hypotenuse in
each triangle
• What do you notice?
Opp*/hyp = 0.6427
• Use your calculator to find Sine
40

3. Conclusion (sine)
• Similar right triangles always have equivalent ratios between
corresponding sides.
• We proved that always (Opp of any angle α /Hyp) is equal to specific
number which is the sine of this angle
• So
sin ˂α = Opp/Hyp

5. More trigonometric Ratios…
Are these triangles similar? Why
• Find the ratios between the short leg to
the hypotenuse in each triangle
• What do you notice?
• Can we consider the short leg as an Opp of
the angle 55.
• The short leg is Adjacent (Adj*) to the
angle 55
Adj/Hyp = 0.5736
• Use your calculator to find Cos 55
• * Adj is the abbreviation of
Adjacent side of the ngle

6. Conclusion (Cosine)
• Similar right triangles always have equivalent ratios between
corresponding sides.
• We prove that always (Adj of any angle α /Hyp) is equal to specific
number which is the Cos of this angle
• So
Cos ˂α = Adj/Hyp

9. Sine–Cosine–Tangent (Trigonometric Ratios)

10. Remember
Sines and Cosines apply only to
right triangles. the opposite side of
the right angle is a Hypotenuse.
Opposite and Adjacent sides will
change according to the acute angle
that you refer to.
Sines and Cosines values are
independent of the dimensions of
the triangle. Sine of a 62 degree
angle will always be .883, regardless
of the size of triangle it is measured
in.

11. Which formula? When? (all in Right triangles)
• Given • Missing term formula
Two sides The 3rd side 𝑎2 + 𝑏2 = 𝑐2 Phythagorean
Altitude, part of the Hyp The legs or the Hyp Geometric means Ratios
One side of special right triangles The other two sides The relation between the sides in
special right triangles
One side, one angle OR two sides The measures of the triangle (all
sides and all angles)
Trigonometric Ratios