Grade 9 Mathematics

1. GOOD
AFTERNOON
CLASS!

3. Six Trigonometric
RATIOS

4. Learning objectives:
• Define trigonometric ratios.
• Illustrate the six
trigonometric ratios (sine,
cosine, tangent, secant,
cosecant, and cotangent.

5. Trigonometry
 The branch of mathematics
dealing with the relations of
the sides and angles of
triangles and with the relevant
functions of any angles.

6. SIX TRIGONOMETRIC
RATIOS
sine
cosine
tangent

7. SIX TRIGONOMETRIC
RATIOS
cosecant
secant
cotangent

8. The value of the
trigonometric ratiodepends
only the measure of the
acute angle of a roght
triangle.
NOTE!!!

9. Discussion
H
O T
hypotenuse
adjacent side
opposite
side

10. First, identify the
hypotenuse, opposite side
and adjacent side of the
given triangle with respect
to the given angle.
REMEMBER!

11. SINE
Trigonometric ratios
It is the ratio between the
lengths of opposite side of the
given angle and the
hypotenuse.
(O)
(H)

12. COSINE
It is the ratio between the
lengths of adjacent side of the
given angle and the
hypotenuse.
(A)
(H)
Trigonometric ratios

13. TANGENT
It is the ratio between the
length of the opposite side and
the length of the adjacent side of
the given angle.
(O)
(A)
Trigonometric ratios

14. Trigonometric ratios
SOH - CAH - TOA

15. Trigonometric ratios
SOH - CAH - TOA

16. Trigonometric ratios
SOH - CAH - TOA

17. Trigonometric ratios
CHO - SHA - CAO

18. example no. 1 Find the six trigonometric
ratios with to angle R of the
given triangle RED.
hypotenuse = 41cm
opposite side = 40cm
adjacent side = 9cm

19. example no. 1
Find the six trigonometric ratios with to angle R of
the given triangle RED.
hypotenuse = 41cm
opposite side = 40cm
adjacent side = 9cm
=
=
=

20. example no. 1
Reciprocal
Reciprocal
Reciprocal

21. If tan find the remaining trigonometric
ratios.
example no. 2
=
hypotenuse?
Pythagorean Theorem
7cm
24cm
𝜽
?

22. example no. 2
Pythagorean Theorem
𝑐=√𝑎2
+𝑏2
𝑎=√𝑐2
−𝑏2
𝑏=√𝑐
2
− 𝑎
2
c = hypotenuse
a = leg
b = leg

23. example no. 2
opposite side
𝑐=√𝑎2
+𝑏2
𝑐=√72
+242
𝑐=√49+576
adjacent side
leg = 7
leg = 24
𝑐=√625
𝑐=25
The length of the
hypotenuse is 25cm
25cm

24. example no. 2
opposite side = 7
adjacent side = 24
hypotenuse = 25
𝒕𝒂𝒏 𝜽 =
𝟕
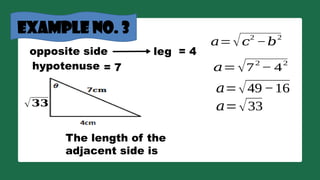
𝟐𝟒
=
=
=
=
=

25. If sin find the remaining trigonometric
ratios.
example no. 3
=
adjacent side?
Pythagorean Theorem
?
4cm
𝜽 7cm

26. example no. 2
Pythagorean Theorem
𝑐=√𝑎2
+𝑏2
𝑎=√𝑐2
−𝑏2
𝑏=√𝑐
2
− 𝑎
2
c = hypotenuse
a = leg
b = leg

27. example no. 3
opposite side
𝑎=√𝑐
2
−𝑏
2
𝑎=√7
2
− 4
2
𝑎=√49−16
hypotenuse
leg = 4
= 7
𝑎=√33
The length of the
adjacent side is
√𝟑𝟑

28. example no. 2
opposite side = 4
adjacent side =
hypotenuse = 7
𝒔𝒊𝒏 𝜽 =
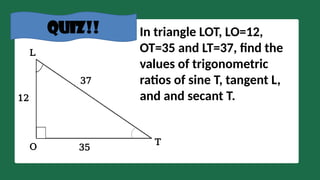
𝟒
𝟕
=
=
=
=
=

29. QUIZ!! In triangle LOT, LO=12,
OT=35 and LT=37, find the
values of trigonometric
ratios of sine T, tangent L,
and and secant T.
37
12
35
L
T
O