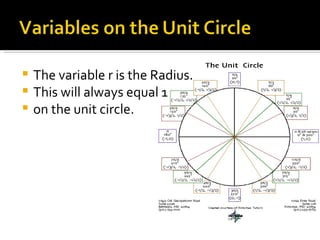
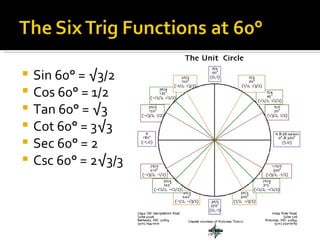
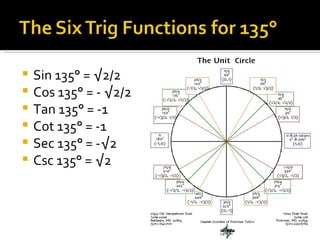
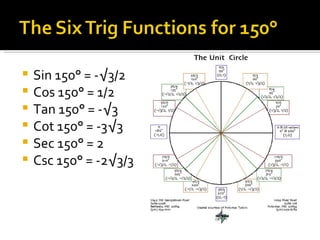
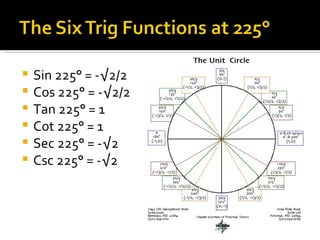
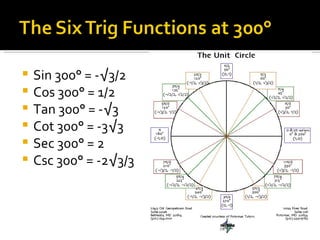
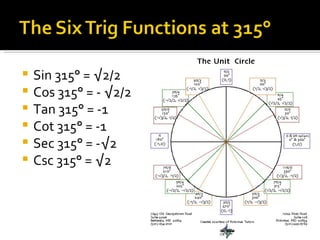
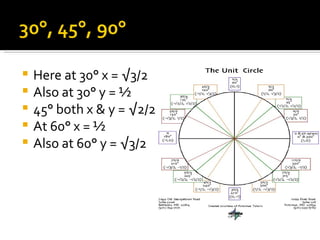
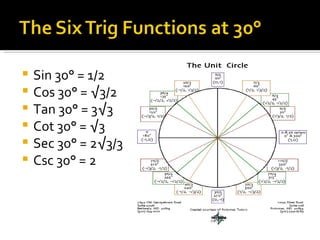
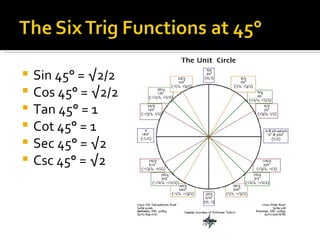
1) The document defines the six trigonometric functions (sine, cosine, tangent, cotangent, secant, cosecant) in terms of the variables x, y, and r on the unit circle, where r is always equal to 1. 2) It provides examples of the trig values of the six functions at 30°, 45°, 60°, 90°, 135°, 150°, 225°, 300°, and 315° by relating x and y to the radii of 30-60-90 and 45-45-90 triangles on the unit circle. 3) The values of the trig functions are reflected across the axes and change signs depending on the quadrant of the unit circle.

1. The Unit Circle

2. Sine t = y/r Cosine t = x/r Tangent t = y/x Cotangent t = x/y Secant t = r/x Cosecant t = r/y

3. The variable r is the Radius. This will always equal 1 on the unit circle.

4. Here at 30° x = √3/2 Also at 30° y = ½ 45° both x & y = √2/2 At 60° x = ½ Also at 60° y = √3/2

5. By using the Pythagorean Theorem the sides of a 45°, 45°, 90° can be found. You will use these on to find all Six Trigonometric Functions. The Hypotenuse must equal 1 therefore the sides opposite 45° is √2/2.

6. Use the Pythagorean Theorem to find the sides of a 30°, 60°, 90° Triangle. Remember the Hypotenuse must equal 1. Therefore, the side opposite 30° = ½. The side opposite 60° = √3/2.

7. Here you can see Sine t = y/r. Cosine t = x/r. Notice that r = 1.

8. Sin 30° = 1/2 Cos 30° = √3/2 Tan 30° = 3√3 Cot 30° = √3 Sec 30° = 2√3/3 Csc 30° = 2

9. Sin 45° = √2/2 Cos 45° = √2/2 Tan 45° = 1 Cot 45° = 1 Sec 45° = √2 Csc 45° = √2

10. Sin 60° = √3/2 Cos 60° = 1/2 Tan 60° = √3 Cot 60° = 3√3 Sec 60° = 2 Csc 60° = 2√3/3

11. Notice that at 90° the (x,y) is (0,1). Sin 90° = 1 Cos 90° = 0 Tan 90° = undefined Cot 90° = 0 Sec 90° = undefined Csc 90° = 1

12. All y values stay the same as in Quadrant I. All x values are negative here. The Six Trig Functions are reflected across the y-axis here. (-cos t, sin t)

13. All x values are negative here. All y values are negative here. The Six Trig Functions are reflected across the origin from Quadrant I. (-cos t, -sin t)

14. All x values stay the same as in Quadrant I. All y values are negative here. The Six Trig Functions are reflected across the x-axis here. (cos t, -sin t)

15. Sin 135° = √2/2 Cos 135° = - √2/2 Tan 135° = -1 Cot 135° = -1 Sec 135° = -√2 Csc 135° = √2

16. Sin 150° = -√3/2 Cos 150° = 1/2 Tan 150° = -√3 Cot 150° = -3√3 Sec 150° = 2 Csc 150° = -2√3/3

17. Sin 225° = -√2/2 Cos 225° = -√2/2 Tan 225° = 1 Cot 225° = 1 Sec 225° = -√2 Csc 225° = -√2

18. Sin 300° = -√3/2 Cos 300° = 1/2 Tan 300° = -√3 Cot 300° = -3√3 Sec 300° = 2 Csc 300° = -2√3/3

19. Sin 315° = √2/2 Cos 315° = - √2/2 Tan 315° = -1 Cot 315° = -1 Sec 315° = -√2 Csc 315° = √2

20. All the Trig Functions in the second Quadrant have the same values as Quad I except the x values are now negative. The same thing happens in Quad III both the x and y values are negative here. In Quad IV the x values are positive and the y values here are negative.