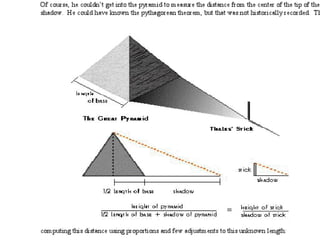
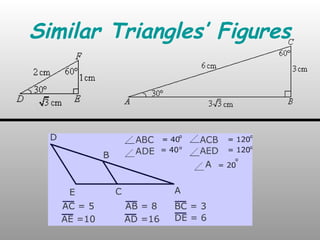
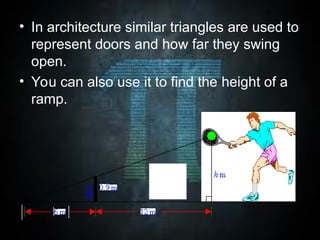
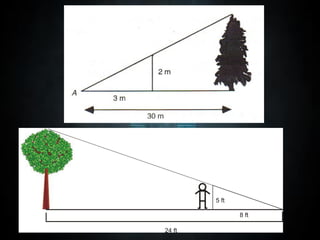
The document discusses the concept of similar triangles, which are geometrical shapes that maintain the same shape through uniform scaling and rotation. It highlights key principles like the Basic Proportionality Theorem, Pythagorean theorem, and various projection theorems, applying to both acute and obtuse triangles. Additionally, it outlines practical applications of these principles in fields such as aerial photography, construction, and architecture.

1. Similar
Triangl
es

2. What is SIMILARITY ??
• Two geometrical objects are called similar if they
both have the same shape.
• One can be obtained from the other by
uniformly scaling (enlarging or shrinking),
possibly with additional rotation.
• Similar to each other – all squares, all circles, all
equilateral triangles, etc
• Not similar to each other – rectangles,
hyperbolas.

3. History
Shadow reckoning was one of the great arts of the ancient
Greeks, and was used extensively by early mathematicians,
especially in measuring the heights of inaccessible objects.
When the Greek mathematician, Thales, visited Egypt, he
astonished the people with his use of shadow reckoning to find
the height of the Great Pyramid.
He first waited until his shadow was exactly as long as he was
tall, then measuring the length of the shadow of the pyramid. Of
course, he couldn’t get into the Pyramid to measure the
distance from the center of the tip to the tip of the shadow…!!!!

5. Similar Triangles
Two triangles and are said to be similar if either
of the following equivalent conditions holds:
• AA similarity - They have two identical angles,
which implies that their angles are all identical.
• SS similarity - Corresponding sides have
lengths in the same ratio.
• SAS similarity - Two sides have lengths in the
same ratio, and the angles included between
these sides have the same measure.

6. Similar Triangles’ Figures

7. Theorems

8. Basic Proportionality Theorem
• The adjacent triangle ABC
has another triangle DEF
inscribed in it such that DE is
parallel to BC.
• Then, by Basic Proportionality
Theorem, AD/DB = AE /EC.
(OR) AD/AB = AE/AC.
Converse of BPT : If AD/AB = AE/AC, then
DE is parallel to BC.

9. Pythagoras’ Theorem
• The adjacent triangle is a
right angled triangle (angle B
= 90 )
ͦ
• In the adjacent figure, AC is
the hypotenuse, BC and AB
are the remaining two sides.
• Then, by Pythagoras’
theorem AC2
= AB2
+ BC2
.
This theorem
was discovered
by Pythagoras
by using
SIMILARITY OF
TRIANGLES….

10. Projection
Theorem 1
• The adjacent triangle ABC is
an acute angled triangle.
• AD is perpendicular to BC.
• By projection theorem 1,
AC2
= AB2
+ BC2
– 2BC.CD
Projection Theorem 1 is applicable for acute
angled triangles only and the theorem is
based on simple addition of two hypotenuses
i.e. AB and AC.

11. Projection Theorem 2
• The adjacent triangle ABC is an
obtuse angles triangle.
• AD is perpendicular to BC
produced to D.
• By projection theorem 2,
AB2
= AC2
+ BC2
+ 2CD.BC
Projection theorem 2 is applicable for
obtuse angled triangles only and the result
is based on simple addition of two
hypotenuses AB and AC.

12. Apollonius Theorem
• In the adjacent triangle
ABC, AM is the median.
• “The sum of the squares of
two sides of a triangle is
equal to twice the sum of
the square on the median
which bisects the third side
and the square of half the
third side.”
• AB2
+ AC2
= 2(AM2
+ BM2
)
Apollonius theorem
is applicable to each
and every triangle
provided that the
median is given.

13. Vertical Angle Bisector
Theorem
• The adjacent triangle ABC
has an angle bisector AD
to BC.
• By vertical angle bisector
theorem, CA/CD = BA/BD.
Converse of Vertical Angle Bisector
Theorem : If a line passing through the
vertex of a triangle divides the base in the
ratio of the other two sides, then it bisects
the vertical angle.

14. Applications of
Similar
Triangles….

15. • Similar triangles It is used in aerial
photography to see the distance from
the sky to the ground.
• It is used in construction to measure
out the room and scale size.
• It is used in light beams to see the
distance from light to the target.
• The Wright Brothers used similar
triangles to prepare their landing.

16. • In architecture similar triangles are used to
represent doors and how far they swing
open.
• You can also use it to find the height of a
ramp.