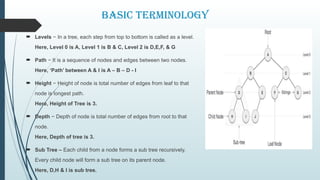
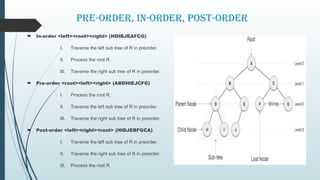
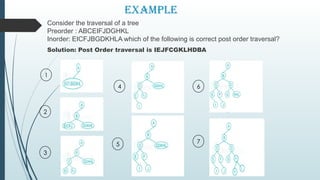
The document covers the concept of trees as a non-linear data structure, explaining basic terminology including nodes, root nodes, edges, and different types of nodes. It details tree traversals (pre-order, in-order, and post-order) and introduces binary tree ADTs, expression trees, and their construction. Additionally, it highlights the applications of trees in various fields such as file storage, 3D rendering, and data compression.

1. DATA STRUCTURES AND
ALGORITHMS
Mrs.V.JAYAVANI., M.S(IT&M)
Assistant Professor
Department of Computer Science
UNIT – III
TREES

2.  Tree ADT
 Tree Traversals
 Binary Tree ADT
 Expression Trees
 Applications of Trees
 Binary Search Tree ADT
SUMMARY
 Threaded Binary Trees
 AVL Trees
 B-Tree
 B+ Tree
 Heap
 Applications of heap

3.  So far we have discussed mainly linear data structures – Arrays, Lists, Stacks and
Queues.
 Now we will discuss a non-linear data structure called tree.

4. TREE
 A tree is a non-linear and hierarchical data structure that
has a group of nodes.
 Tree is a sequence of nodes.
 Trees represent data containing a hierarchical relationship
between elements.
 Eg: Records, Family Trees and Table Contents.
 Consider a parent-child relationship.

6. Basic Terminology
 Node – Node is elements of a Tree.
(A,B,C,D,E, F,G,H,I,J)
 Root Node − The first node is called as Root node. Every tree must
have only one root node.
(A is a root node.)
 Edge – Edge is a connection between one node to another. In a tree
with ‘N’ number of nodes there will be a maximum of ‘N-1’ number of
edges.
No. of Edges = N – 1
= 10 – 1 = 9 Edges
 Parent Node − The node which is a predecessor of any node is
called as Parent Node. It can also be defined as “the node which
has child / children”.
Here, A, B, C, D and E are Parent nodes.

7. Basic Terminology
 Child − The node which is descendant of any node is called as child
node. In a tree all the nodes except root are child nodes.
Here, B,C,D,E,F,G,H,I and J are children nodes.
 Siblings – The nodes with the same parent are called sibling nodes.
Here, B & C, D & E, F & G and H & I are Siblings
 Leaf − The node which does not have any child is called as leaf node. It
is also called as External nodes (or) Terminal nodes.
Here, H, I, J, F and G are Leaf nodes.
 Internal Node – The node which has atleast one child is called as
Internal node. Nodes other than leaf nodes are called as internal nodes.
Here, A, B, C, D and E are Internal nodes
 Degree – The degree of a node is total number of children it has. The
highest degree of a node among all the nodes in a tree is called as
“Degree of Tree”.
Here, Degree of A is 2, Degree of D is 2, Degree of F is 0.

8. Basic Terminology
 Levels − In a tree, each step from top to bottom is called as a level.
Here, Level 0 is A, Level 1 is B & C, Level 2 is D,E,F, & G
 Path − It is a sequence of nodes and edges between two nodes.
Here, ‘Path’ between A & I is A – B – D - I
 Height − Height of node is total number of edges from leaf to that
node is longest path.
Here, Height of Tree is 3.
 Depth − Depth of node is total number of edges from root to that
node.
Here, Depth of tree is 3.
 Sub Tree – Each child from a node forms a sub tree recursively.
Every child node will form a sub tree on its parent node.
Here, D,H & I is sub tree.

9. Tree Traversals
 Traversal is a process to visit all the nodes of a tree and may print their values too.
 All nodes are connected via edges (links) we always start from the root (head)
node.
 There are three ways which we use to traverse a tree
 Pre-order Traversal
 In-order Traversal
 Post-order Traversal

10. Pre-order, in-order, post-order
 In-order <left><root><right> (HDIBJEAFCG)
I. Traverse the left sub tree of R in preorder.
II. Process the root R.
III. Traverse the right sub tree of R in preorder.
 Pre-order <root><left><right> (ABDHIEJCFG)
I. Process the root R.
II. Traverse the left sub tree of R in preorder.
III. Traverse the right sub tree of R in preorder.
 Post-order <left><right><root> (HIDJEBFGCA)
I. Traverse the left sub tree of R in preorder.
II. Traverse the right sub tree of R in preorder.
III. Process the root R.

11. Example
Consider the traversal of a tree
Preorder : ABCEIFJDGHKL
Inorder: EICFJBGDKHLA which of the following is correct post order traversal?
Solution: Post Order traversal is IEJFCGKLHDBA
2
1
5
3
4 6
7

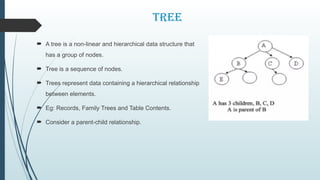
12. Binary Tree ADT
 A binary tree T is defined as a finite set of elements, called nodes,
such that:
T is empty [called the null tree or empty tree]
T contains a distinguished node R, called the root of T form
an ordered pair of disjoint binary trees LT and RT.
 If T does contain a root R.
 Two trees LT and RT are called respectively, the left and right sub
trees of R.
 If LT is non-empty, then its root is called the left successor of R.
 If RT is non-empty, then its root is called the right successor of R.
Binary Tree

13. Binary Tree ADT
 T consists of 10 nodes, represented by the letter A through J.
 The root of T is the node A at the top of the diagram.
 B is a left successor and C is a right successor of that node A.
 The left subtree of he root A consists of the nodes B, D, E, H & I.
 The right subtree of he root A consists of the nodes C, F, G & J.
 Any node N in a binary tree T has either 0,1 or 2 successor.
 The nodes A, B, C and E have two successors.
 The node G have only one successor.
 The nodes D, H, I, F and J have no successors.
 The nodes with no successors are called Terminal nodes.
Binary Tree

14. Expression Trees
 An expression tree is a tree built up from the simple operands as the leaves of binary tree and
operators as the non -leaves of binary tree.
 It is a special kind of binary tree in which:-
(i) Each leaf node contains single operand.
(ii) Each non-leaf node contains a single binary operator.
(iii) The left and right subtrees of an operator node represent sub-expression that must be
evaluated before applying the operator at the root of the subtree.
 The levels in a binary expression tree represent the precedence of operators.
 The operators at the lower level must be evaluated first and then the operators at the next level
and so on and at the last operator at the root node is applied and there by the expression is
evaluated.

15. Expression Trees
 Eg. Expression: - (a-b) * (c+ d )
Prefix expression is *-ab+cd similar to preorder traversal
Postfix expression is ab-cd+* similar to postorder traversal
*
+
-
a b c d

16. Construction of an Expression Tree
(1) From prefix and infix expression
 1. Read the prefix expression, the first element becomes the root.
 2. Now scan the infix expression till you get an element found in step1. Place all
the elements left of this element to the left of it and other element to right of it.
 3. Repeat steps 1 and 2 till all the elements from infix expression gets placed in
tree.
 4. stop

17. Construction of an Expression Tree
(2) From infix and postfix expression
 1. Read the postfix expression, the last element becomes the root.
 2. Now scan the infix expression till you get an element found in step1. Place all the
elements left of this element to the left of it and other element to right of it.
 3. Repeat steps 1 and 2 till all the elements from infix expression get placed in tree.
 4. Stop

18. Construction of an Expression Tree
(3) From a given postfix expression
 1. Read the element from postfix expression from left to right.
 2. If it is an operand then push address of this node onto stack go to step 1.
 3. If the element is an operator then pop twice which gives the address of the two
operands. Create a new node for this operator and attach the operand to the left and
right branch. Push the address of this node onto stack .
 4. If all the elements from postfix expression are not read then go to step 1.
 5. Pop the contents of stack which give the root address of expression tree.
 6. Stop

19. Example
Construct expression tree from following expressions:-
Postfix expression:- 5,3,2,^,*,3,7,3,+,10,/,+/
Infix expression :- (5*3^2)/(3+(7+3)/10)
Sol.
 From postfix we get root i.e. / ,hence (5*3^2) is left subtree and
(3+(7+3)/10) is right subtree.
 Now again find root from postfix for right You get + , now 3 is left and
is (7+3)/10 is right, then 3 is left child.
 In right subtree / is root , (7+3) is left subtree and 10 is right subtree.
 10 is root for right subtree. Now in left subtree + is root and 7is left
child and 3 is right child.
 Similarly for left subtree * is root and 5 is left subtree and 3^2 is right
subtree.
 Now again from right subtree root is ^, 3 is left child and 2 is right
child.
3 2
3
7
+ 10
/
3
Λ
5
+
*
/

20. Applications of Trees
 Directory structure of a file store
 Structure of an arithmetic expressions
 Used in almost every 3D video game to determine what objects need to be
rendered.
 Used in almost every high-bandwidth router for storing router-tables.
 Used in compression algorithms, such as those used by the .jpeg and .mp3 file-
formats.