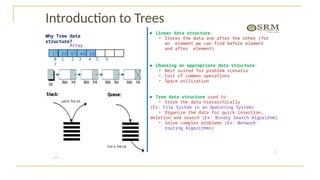
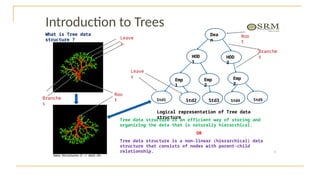
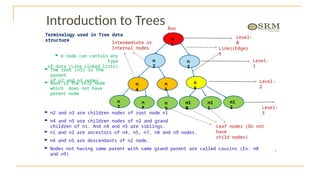
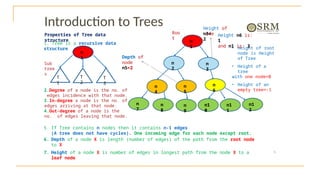
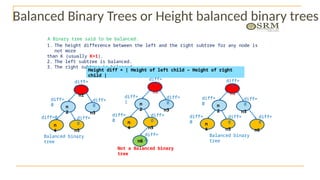
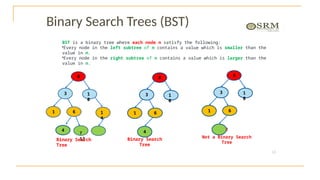
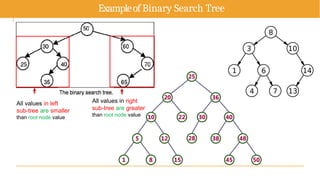
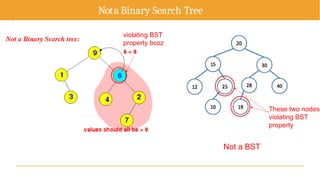
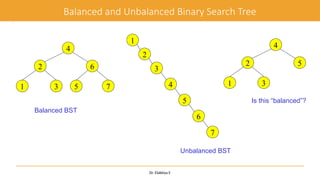
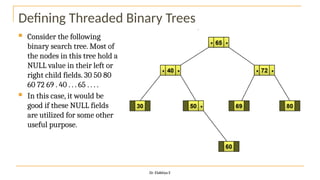
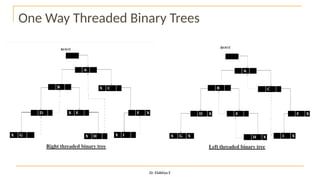
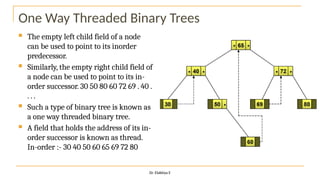
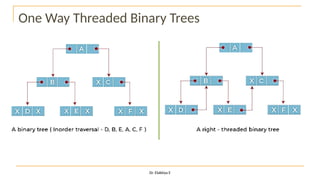
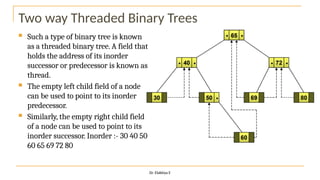
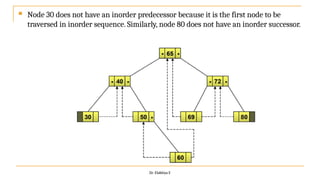
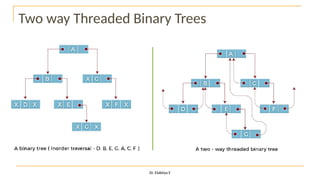
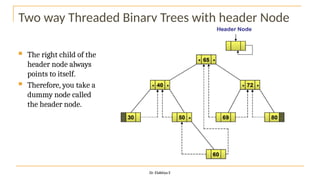
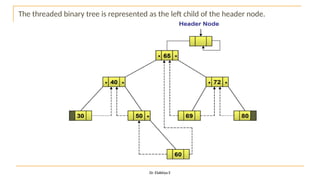
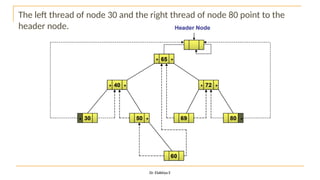
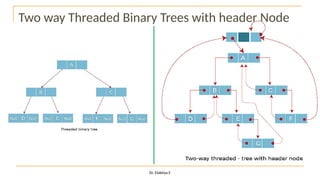
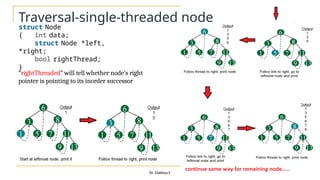
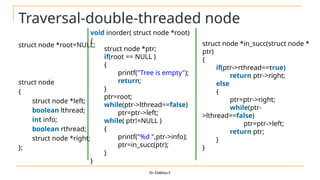
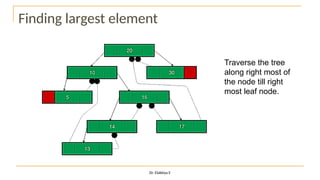
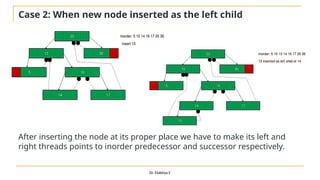
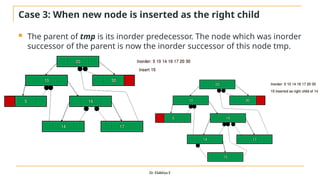
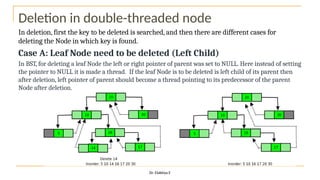
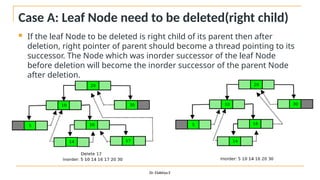
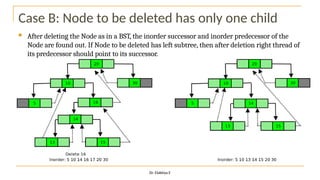
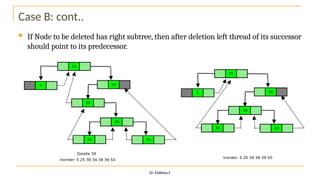
The document discusses advanced topics on tree data structures including threaded binary trees, AVL trees, B-trees, and their respective operations like insertion and deletion. It highlights key properties and terminology associated with trees, such as height, depth, and balancing methods to maintain efficiency in operations. Additionally, various types of threaded binary trees and their traversal techniques are explained, underscoring their utility in optimizing tree structures.

1. DATA STRUCTURES-II
CSE 203
Dr. Elakkiya

2. UNIT III: ADVANCED TOPICS ON TREES
 Threaded Binary Tree, Traversal of Threaded Binary Tree, Operations on a Threaded
Binary Search Tree: Insertion, deletion, finding largest element, Deleting Threaded
Binary Tree.
 AVL Trees: Height of AVL Tree, Operations on an AVL Tree: insertion, deletion. m-
Way search tree: Index and Searching, B-Tree, Operations on B-Tree: Searching,
Inserting, Deleting from a B-Tree, B+ Tree, Operations on B+-Tree: Searching,
Inserting, Deleting from a B+-Tree, B* tree.
Dr. Elakkiya E

3. Data Structures-I--> Unit-
IV:
17 23 97 44 33
Array
0 1 2 3 4 5 6
7
Introduction to Trees
Why Tree data
structure?
► Linear data structure:
• Stores the data one after the other (for
an element we can find before element
and after element).
► Choosing an appropriate data structure:
• Best suited for problem scenario
• Cost of common operations
• Space utilization
► Tree data structure used to:
• Store the data hierarchically
(Ex: File System in an Operating System)
• Organize the data for quick insertion,
deletion and search (Ex: Binary Search Algorithm)
• Solve complex problems (Ex: Network
routing Algorithms)
3

4. Introduction to Trees
Dea
n
HOD
1
HOD
2
Emp
1
Emp
2
Emp
2
Std1 Std2 Std3 Std4 Std5
Logical representation of Tree data
structure
Branche
s
Leave
s
Roo
t
What is Tree data
structure ?
Tree data structure is an efficient way of storing and
organizing the data that is naturally hierarchical.
OR
Tree data structure is a non-linear (hierarchical) data
structure that consists of nodes with parent-child
relationship.
Roo
t
Leave
s
Branche
s
4

5. 5
n
1
n
2
n
3
n
4
n
5
n
6
n
7
n
8
n
9
n1
0
n1
1
n1
2
Roo
t
Introduction to Trees
Terminalogy used in Tree data
structure
Links(Edges
)
Level-
0
Level-
2
Level-
1
Level-
3
Intermediate or
Internal nodes
Leaf nodes (Do not
have
child nodes)
► A node can contain any
type
of data (Like Linked lists)
► The root (n1) is the
parent
of n2 and n3 nodes
► Root is the only node
which does not have
parent node
► n2 and n3 are children nodes of root node n1
► n4 and n5 are children nodes of n2 and grand
children of n1. And n4 and n5 are siblings.
► n1 and n2 are ancestors of n4, n5, n7, n8 and n9 nodes.
► n4 and n5 are descendants of n2 node.
► Nodes not having same parent with same grand parent are called cousins (Ex: n8
and n9)
► A node can contain any
type
of data (Like Linked lists)
► The root (n1) is the
parent
of n2 and n3 nodes
► Root is the only node
which does not have
parent node

6. Introduction to Trees
Properties of Tree data
structure n
1
n
2
n
3
n
4
n
5
n
6
n
7
n
8
n
9
n1
0
n1
1
n1
2
Roo
t
n
1
1. Tree is a recursive data
structure
Sub
tree
s
T
3
T
1
T
2
5. If Tree contains n nodes then it contains n-1 edges
(A tree does not have cycles). One incoming edge for each node except root.
6. Depth of a node X is length (number of edges) of the path from the root node
to X
7. Height of a node X is number of edges in longest path from the node X to a
leaf node
Depth of
node
n5=2
Height of
node
n3=
2
• Height of root
node is Height
of Tree
• Height of a
tree
with one node=0
• Height of an
empty tree=-1
Height n6 is:
1
and n1 is: 3
6
2.Degree of a node is the no. of
edges incidence with that node.
3.In-degree a node is the no. of
edges arriving at that node.
4.Out-degree of a node is the
no. of edges leaving that node.

7. Balanced Binary Trees or Height balanced binary trees
n
2
diff=
1
n1
diff=0
n
4
A Binary tree said to be balanced:
1. The height difference between the left and the right subtree for any node is
not more
than K (usually K=1).
2. The left subtree is balanced.
3. The right subtree is balanced.
Height diff = | Height of left child – Height of right
child |
diff=
0
diff=
0
n3
diff=
0
n5
n
2
n
4
diff=
1
diff=
0
n3
diff=
0
n5
n6
Not a Balanced binary
tree
diff=
0
diff=
0
diff=
2
n1
n
2
n
4
diff=
0
diff=
0
n3
diff=
0
n5
diff=
0
diff=
0
n1
diff=
0
n6
Balanced binary
tree
Balanced binary
tree

8. 12
BST is a binary tree where each node n satisfy the following:
•Every node in the left subtree of n contains a value which is smaller than the
value in n.
•Every node in the right subtree of n contains a value which is larger than the
value in n.
Binary Search Trees (BST)
8
3 1
0
1 6 1
4
4
7
13
8
3 1
0
1 6
4
Binary Search
Tree
8
3 1
0
1 6
2
Not a Binary Search
Tree
Binary Search
Tree

9. Exampleof Binary Search Tree
All values in right
sub-tree are greater
than root node value
All values in left
sub-tree are smaller
than root node value

10. Nota Binary Search Tree
Not a BST
These two nodes
violating BST
property
violating BST
property bcoz

11. Problem with Binary Search Tree
• The disadvantage of a binary search tree is that its height can be as large as (n – 1).
• This means that the time needed to perform insertion, deletion and many other
operations can be O(n) in the worst scenario.
• So, we want a tree with small height.
• A binary tree with n node has height at least
• Thus, our goal is to keep the height of a binary search tree O(log2 n).
• Hence to achieve the goal, some balanced binary search tree is required. Examples are
AVL tree, Splay tree, B-Tree, B+ Tree, Red-black tree etc.
h = ⌊log2𝑛⌋

12.  What happens when you Insert elements in BST in ascending order
(or descending order?
 Insert: 2, 4, 6, 8, 10, 12 into an empty BST.
Problem: Lack of “balance”.
 compare depths of left and right subtree.
 height of tree = n – 1 ; if tree grows in one direction only
where n is the total no. of nodes in the BST
 Searching, insertion, deletion, find-min, find-max
may take O(h) = O(n) time to perform the task.
Problem with Binary Search Tree- Worst Case Scenario
2
4
6
8
10
12
Dr. Elakkiya E

13. 1
5
2
4
3
7
6
4
2 6
5 7
1 3
4
2 5
1 3
Is this “balanced”?
Balanced and Unbalanced Binary Search Tree
Balanced BST
Unbalanced BST
Dr. Elakkiya E

14.  Many other Trees exist for keeping binary search trees balanced:
› Adelson-Velskii and Landis (AVL) Tree (height-balanced tree)
› Splay Tree and other self-adjusting trees
› B-Tree and other multiway search trees
› B+ Tree
› Red-Black Tree
Balancing Binary Search Trees
Dr. Elakkiya E

15. Threaded Binary Tree
 A binary tree with thread(s) is known as threaded binary tree. In a threaded binary
tree a node may contain pointer to its child node or thread to some higher node in
the node. The higher node to which the thread points in the tree is determined
according to the tree traversal technique used (i.e. preorder, inorder, postorder).
 There are three methods to apply thread binary tree. Each method corresponds to a
particular type of tree traversal:
 Preorder threading: on this, the threads are applied to the higher node
containing the preorder traversal of the tree.
 Inorder threading: the threads are applied considering the inorder traversal.
 Postorder threading: the thread are applied consider the postorder traversal.
Dr. Elakkiya E

16. Threaded Binary Tree
 In a binary search tree, there are many nodes that have an empty left child or empty
right child or both.
 You can utilize these fields in such a way so that the empty left child of a node
points to its inorder predecessor and empty right child of the node points to its
inorder successor,
 One way threading:- A thread will appear in a right field of a node and will point
to the next node in the inorder traversal. •
 Two way threading:- A thread will also appear in the left field of a node and will
point to the preceding node in the inorder traversal
Dr. Elakkiya E

17. Defining Threaded Binary Trees
 Consider the following
binary search tree. Most of
the nodes in this tree hold a
NULL value in their left or
right child fields. 30 50 80
60 72 69 . 40 . . . 65 . . . .
 In this case, it would be
good if these NULL fields
are utilized for some other
useful purpose.
Dr. Elakkiya E

18. One Way Threaded Binary Trees
 In this, a thread appears either in the right link field or in the left link field of the
node. If the thread appears in the right link filed of the node then points to the next
node in the inorder traversal of the tree i.e. it points to the in order successor of the
node. Such tree is known as right threaded binary tree.
 If the thread appears in the left link field of the node. It points to the preceding node
in the inorder traversal of the tree. Such a tree is known as left threaded binary tree.
As, the threading is done according to the inorder traversal, hence the tree is
referred as in-threaded binary tree.
Dr. Elakkiya E

19. One Way Threaded Binary Trees
Dr. Elakkiya E

20. One Way Threaded Binary Trees
 The empty left child field of a node
can be used to point to its inorder
predecessor.
 Similarly, the empty right child field of
a node can be used to point to its in-
order successor. 30 50 80 60 72 69 . 40 .
. . .
 Such a type of binary tree is known as
a one way threaded binary tree.
 A field that holds the address of its in-
order successor is known as thread.
In-order :- 30 40 50 60 65 69 72 80
Dr. Elakkiya E

21. One Way Threaded Binary Trees
Dr. Elakkiya E

22. Two way Threaded Binary Trees
 Such a type of binary tree is known
as a threaded binary tree. A field that
holds the address of its inorder
successor or predecessor is known as
thread.
 The empty left child field of a node
can be used to point to its inorder
predecessor.
 Similarly, the empty right child field
of a node can be used to point to its
inorder successor. Inorder :- 30 40 50
60 65 69 72 80
Dr. Elakkiya E

23.  Node 30 does not have an inorder predecessor because it is the first node to be
traversed in inorder sequence. Similarly, node 80 does not have an inorder successor.
Dr. Elakkiya E

24. Two way Threaded Binary Trees
Dr. Elakkiya E

25. Two way Threaded Binary Trees with header Node
 The right child of the
header node always
points to itself.
 Therefore, you take a
dummy node called
the header node.
Dr. Elakkiya E

26. The threaded binary tree is represented as the left child of the header node.
Dr. Elakkiya E

27. The left thread of node 30 and the right thread of node 80 point to the
header node.
Dr. Elakkiya E

28. Two way Threaded Binary Trees with header Node
Dr. Elakkiya E

29. Representing a Threaded Binary Tree
 The structure of a node in a threaded binary tree is a bit different from that of a
normal binary tree.
 Unlike a normal binary tree, each node of a threaded binary tree contains two extra
pieces of information, namely left thread and right thread.
 The left and right thread fields of a node can have two values:
 1: Indicates a normal link to the child node
 0: Indicates a thread pointing to the inorder predecessor or inorder successor
Dr. Elakkiya E

30. Traversal-single-threaded node
Dr. Elakkiya E
struct Node
{ int data;
struct Node *left,
*right;
bool rightThread;
}
“rightThreaded” will tell whether node’s right
pointer is pointing to its inorder successor

31. Traversal-single-threaded node
// Function to find leftmost node in a tree
rooted with n
struct Node* leftMost(struct Node* n)
{
if (n == NULL)
return NULL;
while (n->left != NULL)
n = n->left;
return n;
}
Dr. Elakkiya E
// Inorder traversal in a threaded binary tree
void inOrder(struct Node* root)
{
struct Node* cur = leftMost(root);
while (cur != NULL) {
printf("%d ", cur->data);
// If this node is a thread node, then go to inorder
//successor
if (cur->rightThread)
cur = cur->right;
else
// Else go to the leftmost child in right subtree
cur = leftmost(cur->right);
}
}

32. Traversal-double-threaded node
struct node *root=NULL;
struct node
{
struct node *left;
boolean lthread;
int info;
boolean rthread;
struct node *right;
};
Dr. Elakkiya E
void inorder( struct node *root)
{
struct node *ptr;
if(root == NULL )
{
printf("Tree is empty");
return;
}
ptr=root;
while(ptr->lthread==false)
ptr=ptr->left;
while( ptr!=NULL )
{
printf("%d ",ptr->info);
ptr=in_succ(ptr);
}
}
struct node *in_succ(struct node *
ptr)
{
if(ptr->rthread==true)
return ptr->right;
else
{
ptr=ptr->right;
while(ptr-
>lthread==false)
ptr=ptr->left;
return ptr;
}
}

33. Finding largest element
Dr. Elakkiya E
Traverse the tree
along right most of
the node till right
most leaf node.

34. Insertion in double-threaded node
struct Node
{ struct Node *left, *right;
int info;
boolean lthread; // false if left pointer points to predecessor in Inorder Traversal
boolean rthread; // false if right pointer points to successor in Inorder Traversal
};
Let tmp be the newly inserted node. There can be three cases during insertion:
Case 1: Insertion in empty tree
Both left and right pointers of tmp will be set to NULL and new node becomes the root.
root = tmp;
tmp -> left = NULL;
tmp -> right = NULL;
Dr. Elakkiya E

35. Case 2: When new node inserted as the left child
Dr. Elakkiya E
After inserting the node at its proper place we have to make its left and
right threads points to inorder predecessor and successor respectively.

36. Case 2: When new node inserted as the left child
 After inserting the node at its proper place we have to make its left
and right threads points to inorder predecessor and successor
respectively. The node which was inorder successor. So the left and
right threads of the new node will be-
 tmp -> left = par ->left;
 tmp -> right = par;
 Before insertion, the left pointer of parent was a thread, but after
insertion it will be a link pointing to the new node.
 par -> lthread = false;
 par -> left = temp;
Dr. Elakkiya E

37. Case 3: When new node is inserted as the right child
 The parent of tmp is its inorder predecessor. The node which was inorder
successor of the parent is now the inorder successor of this node tmp.
Dr. Elakkiya E

38. Case 3: When new node is inserted as the right
child
 The parent of tmp is its inorder predecessor. The node which was
inorder successor of the parent is now the inorder successor of this
node tmp. So the left and right threads of the new node will be-
 tmp -> left = par;
 tmp -> right = par -> right;
 Before insertion, the right pointer of parent was a thread, but after
insertion it will be a link pointing to the new node.
 par -> rthread = false;
 par -> right = tmp;
Dr. Elakkiya E

39. Insertion in double-threaded node
Dr. Elakkiya E
struct Node
{ struct Node *left, *right;
int info;
bool lthread;
bool rthread;
};
structNode *insert(structNode *root, intikey)
{ // Searching for a Node with given value
Node *ptr = root;
Node *par = NULL; // Parent of key to be inserted
while(ptr != NULL)
{ // If key already exists, return
if(ikey == (ptr->info))
{ printf("Duplicate Key !n");
returnroot;
}
par = ptr; // Update parent pointer
if (ikey < ptr->info) // Moving on left subtree.
{ if (ptr -> lthread == false)
ptr = ptr -> left;
else
break;
}
else// Moving on right subtree.
{ if (ptr->rthread == false)
ptr = ptr -> right;
else
break;
}
} // End while

40. Dr. Elakkiya E
// Create a new node:Case-I
Node *tmp = new Node;
tmp -> info = ikey;
tmp -> lthread = true;
tmp -> rthread = true;
if (par == NULL)
{ root = tmp;
tmp -> left = NULL;
tmp -> right = NULL;
}
else if (ikey < (par -> info))
{
tmp -> left = par -> left;
tmp -> right = par;
par -> lthread = false;
par -> left = tmp;
}
else
{
tmp -> left = par;
tmp -> right = par -> right
par -> rthread = false;
par -> right = tmp;
}
return root;
}

41. Dr. Elakkiya E
void inorder(struct Node *root)
{
if (root == NULL)
printf("Tree is empty");
// Reach leftmost node
struct Node *ptr = root;
while (ptr -> lthread ==
false)
ptr = ptr -> left;
// One by one print
successors
while (ptr != NULL)
{
printf("%d ",ptr ->
info);
ptr =
inorderSuccessor(ptr);
}
}
struct Node *inorderSuccessor(struct Node *ptr)
{
// If rthread is set, we can quickly find
if (ptr -> rthread == true)
return ptr->right;
// Else return leftmost child of right subtree
ptr = ptr -> right;
while (ptr -> lthread == false)
ptr = ptr -> left;
return ptr;
}

42. Deletion in double-threaded node
In deletion, first the key to be deleted is searched, and then there are different cases for
deleting the Node in which key is found.
Case A: Leaf Node need to be deleted (Left Child)
In BST, for deleting a leaf Node the left or right pointer of parent was set to NULL. Here instead of setting
the pointer to NULL it is made a thread. If the leaf Node is to be deleted is left child of its parent then
after deletion, left pointer of parent should become a thread pointing to its predecessor of the parent
Node after deletion.
Dr. Elakkiya E

43. Case A: Leaf Node need to be deleted(right child)
 If the leaf Node to be deleted is right child of its parent then after
deletion, right pointer of parent should become a thread pointing to its
successor. The Node which was inorder successor of the leaf Node
before deletion will become the inorder successor of the parent Node
after deletion.
Dr. Elakkiya E

44. Case B: Node to be deleted has only one child
 After deleting the Node as in a BST, the inorder successor and inorder predecessor of the
Node are found out. If Node to be deleted has left subtree, then after deletion right thread of
its predecessor should point to its successor.
Dr. Elakkiya E

45. Case B: cont..
 If Node to be deleted has right subtree, then after deletion left thread of its successor
should point to its predecessor.
Dr. Elakkiya E

46. Dr. Elakkiya E
struct Node* delThreadedBST(struct Node* root, int dkey)
{ // Initialize parent as NULL and pointer Node as
root.
struct Node *par = NULL, *ptr = root;
int found = 0; // Set true if key is found
// Search key in BST : find Node and its parent.
while (ptr != NULL) {
if (dkey == ptr->info) {
found = 1;
break;
}
par = ptr;
if (dkey < ptr->info) {
if (ptr->lthread == false)
ptr = ptr->left;
else
break;
}
else {
if (ptr->rthread == false)
ptr = ptr->right;
else
break;
}
}
if (found == 0)
printf("dkey not present in treen");
// Two Children
else if (ptr->lthread == false && ptr->rthread == fals
root = caseC(root, par, ptr);
// Only Left Child
else if (ptr->lthread == false)
root = caseB(root, par, ptr);
// Only Right Child
else if (ptr->rthread == false)
root = caseB(root, par, ptr);
// No child
else
root = caseA(root, par, ptr);
return root;
}
Delete
threaded
binary tree

47. Case A: Leaf Node need to be deleted
Dr. Elakkiya E
struct Node* caseA(struct Node* root, struct Node* par,struct Node* ptr)
{
// If Node to be deleted is root
if (par == NULL)
root = NULL;
// If Node to be deleted is left of its parent
else if (ptr == par->left) {
par->lthread = true;
par->left = ptr->left;
}
else {
par->rthread = true;
par->right = ptr->right;
}
// Free memory and return new root
free(ptr);
return root;
}

48. Case B: Node to be deleted has only one child
Dr. Elakkiya E
struct Node* caseB(struct Node* root, struct Node* par,struct Node*
ptr)
{ struct Node* child;
// Initialize child Node to be deleted has left child.
if (ptr->lthread == false)
child = ptr->left;
// Node to be deleted has right child.
else
child = ptr->right;
// Node to be deleted is root Node.
if (par == NULL)
root = child;
// Node is left child of its parent.
else if (ptr == par->left)
par->left = child;
else
par->right = child;
// Find successor and predecessor
Node* s = inSucc(ptr);
Node* p = inPred(ptr);
// If ptr has left subtree.
if (ptr->lthread == false)
p->right = s;
// If ptr has right subtree.
else {
if (ptr->rthread == false)
s->left = p;
}
free(ptr);
return root;
}

49. Case C: Node to be deleted has two children
struct Node* caseC(struct Node* root, struct Node* par, struct Node*
ptr)
{ // Find inorder successor and its parent.
struct Node* parsucc = ptr;
struct Node* succ = ptr->right;
// Find leftmost child of successor
while (succ->left != NULL) {
parsucc = succ;
succ = succ->left;
}
ptr->info = succ->info;
if (succ->lthread == true && succ->rthread == true)
root = caseA(root, parsucc, succ);
else
root = caseB(root, parsucc, succ);
return root;
}
Dr. Elakkiya E

50. Case C: Node to be deleted has two children
 We find inorder successor of Node ptr (Node to be deleted) and
then copy the information of this successor into Node ptr. After this
inorder successor Node is deleted using either Case A or Case B.
 If Node to be deleted has left subtree, then after deletion right
thread of its predecessor should point to its successor.
Dr. Elakkiya E

51. THANK YOU