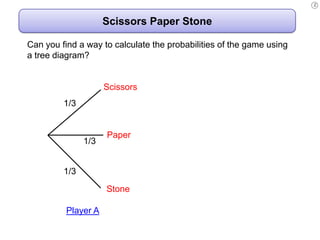
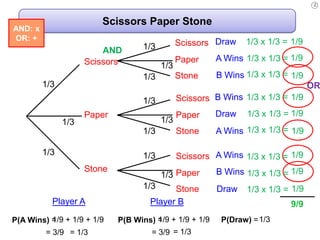
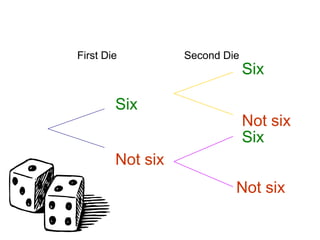
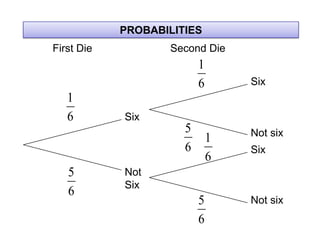
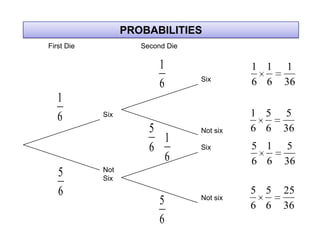
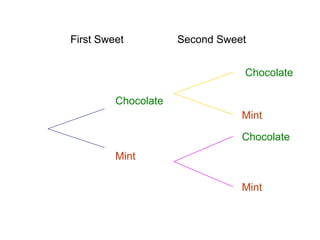
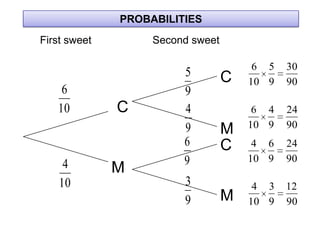
The document describes how to use tree diagrams to calculate conditional probabilities through games like scissors-paper-stone and dice rolls, as well as sweets selection. It provides instructions for playing a game, tabulating results, and converting tallies into probabilities. Additionally, it includes problems involving calculating probabilities of drawing two similar sweets from a tin.

1. Tree Diagrams
Learning Intention:
Draw and use a tree diagram to find conditional probabilities.

2. Z

3. Z
Scissors Paper Stone
 Create the following table to
complete as you play
Result Tally Total Probability
A Wins
B Wins
Draw
 Play the game 30 times
 Add up your tally for the Total
 Scissors beats paper (cuts it)  Fill in the 3 probabilities (these are
the Total / 30)
 Paper beats stone (wraps it)  Use the calculator these into
 Stone beats scissors (blunts it) convert these into decimals
 Enter your results into the
 Showing the same is a draw class spreadsheet

4. Z
Scissors Paper Stone
Can you find a way to calculate the probabilities of the game using
a tree diagram?
Scissors
1/3
Paper
1/3
1/3
Stone
Player A

5. Z
Scissors Paper Stone
AND: x
OR: +
1/3 Scissors Draw 1/3 x 1/3 = 1/9
AND
Scissors Paper A Wins 1/3 x 1/3 = 1/9
1/3
1/3 Stone B Wins 1/3 x 1/3 = 1/9
1/3 OR
1/3 Scissors B Wins 1/3 x 1/3 = 1/9
Paper Paper Draw 1/3 x 1/3 = 1/9
1/3 1/3
1/3 Stone A Wins 1/3 x 1/3 = 1/9
1/3 1/3 Scissors A Wins 1/3 x 1/3 = 1/9
Stone B Wins 1/3 x 1/3 = 1/9
1/3 Paper
1/3 Stone Draw 1/3 x 1/3 = 1/9
Player A Player B 9/9
P(A Wins) = /9 + 1/9 + 1/9
1 P(B Wins) =/9 + 1/9 + 1/9
1 P(Draw) = 1/3
= 3/9 = 1/3 = 3/9 = 1/3

6. Two Dice

7. First Die Second Die
Six
Six
Not six
Six
Not six
Not six

8. PROBABILITIES
First Die Second Die
1
6 Six
1
6 Six
5 Not six
1
6 Six
6
5 Not
Six
6
5 Not six
6

9. PROBABILITIES
First Die Second Die
1 1 1 1
Six 6 6 36
6
1
6 Six 1 5 5
5 Not six 6 6 36
1
6 Six 5 1 5
6 6 6 36
Not
5 Six
6 Not six
5 5 25
5 6 6 36
6

10. Colin has a tin of sweets:
6 chocolates and 4 mints
Produce a tree diagram to
show the probabilities of
taking one sweet followed by
another sweet.
What is the probability of
taking two of the same type?

11. First Sweet Second Sweet
Chocolate
Chocolate
Mint
Chocolate
Mint
Mint

12. PROBABILITIES
First sweet Second sweet
6 5 30
5 C 10 9 90
6 9
10 C 4 6 4 24
10 9 90
9 M
6 C 4 6 24
9 10 9 90
4 M
10 3 4 3 12
9 M 10 9 90

13. What is the probability of taking
two of the same type?
6 5 30
Chocolate and chocolate =
10 9 90
4 3 12
Mint and mint =
10 9 90
30 12 42
So two of the same =
90 90 90

14. Task
Make up a story of your own
Draw a tree diagram
Label all possible outcomes