The document presents a study on forecasting the energy output from a combined cycle thermal power plant (CCPP) using deep learning models, particularly artificial neural networks (ANN) and deep neural networks (DNN). Various operating thermal parameters such as ambient pressure, vacuum, relative humidity, and temperature were modeled, resulting in acceptable prediction accuracy, with R-squared values reaching up to 0.94. The study concludes that a single-layer ANN is recommended for its computational efficiency, while the models successfully predict the plant's energy output under varying atmospheric conditions.
![Case Studies in Thermal Engineering 28 (2021) 101693
Available online 7 December 2021
2214-157X/© 2021 The Author. Published by Elsevier Ltd. This is an open access article under the CC BY-NC-ND license
(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Forecasting the energy output from a combined cycle thermal
power plant using deep learning models
C. Ahamed Saleel
Department of Mechanical Engineering, College of Engineering, King Khalid University, PO Box 394, Abha, 61421, Saudi Arabia
A R T I C L E I N F O
Keywords:
Power plant
Energy output
Neural networks
Modelling
Thermal parameters
A B S T R A C T
The energy output from a combined cycle power plant (CCPP) varying with the operating thermal
parameters like ambient pressure, vacuum, relative humidity, and relative temperature is
modelling using different approaches. The huge data obtained from the experimental readings is
found to be highly non-linear using the data visualization technique. The energy output from the
CCPP reduces linearly with the temperature and non-linearly with pressure. A mathematical
model is developed for the predictions of the energy output. Modelling using sequential API and
functional API based artificial neural network (SANN and FANN) having single hidden layer is
carried out. Finally, energy output modelling using sequential API and functional API based deep
ANN (SDNN and FDNN) is also performed. The residuals of the predicted and experimental ob
servations indicate that the error is acceptable and it lies uniformly above and below the
regression line. The R-squared value of the mathematical model is 0.93 and 0.94 during training
and testing. The obtained R-squared value of the ANN and DNN using sequential and functional
API is 0.94. The training and testing of all the models are successful and these models have shown
a great compatibility in predicting the energy output of a CCPP. The ANN model with single layer
and deep layer has no difference in accuracy hence the former one is recommended as it is
computationally less expensive.
1. Introduction
In all over the world, electricity is the main driving soul of a current civilization and is the key essential resources to human ac
complishments. For the proper function of the economy and our society, we are in the requirement of a huge amount of electrical
power and due to continuous demand of electricity the use of combined cycle power plant (CCPP) is increasing day by day. To provide
needed amount of electricity to the human communities the power plants are established in large scale. The key concern in this favour
is the production of electrical power by keeping reliable and favourable power generation system. In thermal power plants generally,
thermodynamical methods are used to analyse the systems accurately for its operation. This method uses many number assumptions
and parameters to solve the thousands of nonlinear equations; whose elucidation takes too much effort and computational time or
sometimes it is difficulty to solve these equations without these assumptions [1,2].
To eradicate this barrier, in recent days the machine learning (ML) methods are commonly used as substitute to thermodynamical
methods and mathematical modelling to study the systems for random output and input patterns [1,3,4]. In ML approach, envisaging
an actual value called as regression is the most common problem. To control the system response and for predicting an actual numeric
value, the ML approach uses machine learning algorithms. Using ML approach and its algorithms, the many realistic and everyday
E-mail addresses: ahamedsaleel@gmail.com, ahamedsaleel@gmail.com.
Contents lists available at ScienceDirect
Case Studies in Thermal Engineering
journal homepage: www.elsevier.com/locate/csite
https://doi.org/10.1016/j.csite.2021.101693
Received 11 April 2021; Received in revised form 7 November 2021; Accepted 3 December 2021](https://image.slidesharecdn.com/1-s2-240723001757-a9dcae83/85/Total-enegy-forecasting-using-deep-learning-1-320.jpg)
![Case Studies in Thermal Engineering 28 (2021) 101693
2
problems can be elucidated as regression problems to improve prognostic models [5].
The Artificial Neural Networks (ANNs) is one of the methods of ML. Using ANNs the environmental conditions and nonlinear
relationships are considered as inputs of the ANNs model, and the power generates is considered as the output of the model. Using ANN
model, we can calculate the power output of the power plant by giving the various environmental conditions.
ANNs were proposed originally in the mid of 20th century as a human brain computational model. At that time, their use was
restricted due to the available of limited computational power and few theoretically unsolved problems. Though, they have been
applied and studied increasingly in recent days due to their availability if computational power and datasets [6]. In modern thermal
power plants, a huge quantity of parametric data is kept over long periods of time; hence, a big data created on the active data is
continuously readily available without any extra cost [7].
The present study deals with various ML regression approaches for an extrapolation study of a CCPP as a thermodynamic system.
The CCPP involves two heat recovery systems, one steam turbine, and two gas turbines. Using ML techniques, the calculation of
electrical power output of a CCPP is considered as a one real-life critical problem. For the economic operation and efficiency of a power
plant, the calculation of electrical power output for full and base load of a power plant is very important. It also helps to improve the
revenue from obtainable Megawatt hours (MWh). The gas turbine sustainability and reliability is highly depending on calculation of its
generation of power.
The output power of gas turbine mainly depends on the atmospheric parameters such as relative humidity, atmospheric pressure
and atmospheric temperature. The output power of a steam turbine has direct correlation with exhaust vacuum. The effects of at
mospheric disorders are deliberated in the literature for the calculation of electrical power (PE) by using ML intelligence systems i.e.,
ANNs [1,8,9]. Several investigations have deliberated ANN model to numerous engineering systems [10–17]. Many investigators
conveyed the reliability and feasibility of ANN models as analysis and simulation tool for different power plant components and
processes [18–25]. Comparatively limited studies have deliberated the use of steam turbine (ST) in a CCPP [3,7,26,27]. Back prop
agation modelling of nanofluids based on MXene nanoparticles was modelled by Afzal et al. [20] which provided an excellent pre
diction of the viscosity and shear stress of the nanofluid. A similar work on the battery Nusselt number, base pressure predictions at
sonic and supersonic numbers by the same authors is proposed in Refs. [21–25].
Using ANN model in Ref. [1] the various effects such as wind velocity and its direction, relative humidity, ambient pressure,
ambient temperature on the power plant are examined based on the measured information from the power plant. For varying local
atmospheric conditions, in Ref. [9] the ANN model is used to calculate the performance and operational parameters of a gas turbine. In
Refs. [8,26], researchers compared different ML methods to calculate the full load output of electrical power of a base load operated
CCPP.
The modelling of stationary gas turbine is also done by using ANNs. In Ref. [28], the ANN system is developed and effectively used
for studying the behaviours of gas turbine for different range of working points starting from full speed full load and no-load situations.
The radial basis function (RBF) and Multi-Layer Perception (MLP) networks are effectively used in Ref. [29] for finding start-up stage of
stationary gas turbine. In Refs. [30,31], authors used different designs of MLP method to estimate the electrical power output and
performance of the CCPP by using variable solvers, hidden layer configurations and activation functions.
For identification of gas turbine in Ref. [32], the Feed Forward Neural Networks (FFNNs) and dynamic linear models are compared
and found Neural Networks (NNs) as a prognosticator model to pinpoint superior enactments than the vigorous linear models. The
ANNs models are also effectively employed in isolation, fault detection, anomaly detection and performance analysis of gas turbine
engines [2,33,34]. In Refs. [35–37], CCPP total electrical energy power output is predicted by using FFNNs which is fully based on
novel trained particle swarm optimization method. They used atmospheric pressure, vacuum, relative humidity and ambient tem
perature as input factors to calculate hourly average power output of the CCPP. An ANN based ML processing tool and its predictive
approach is successfully used in Ref. [38] CCPPs to study and analyse the environmental impact on CCPP generation. In Ref. [39], the
Internet of Things (IoT) based micro-controller automatic information logger method is employed to accumulate environment data in
CCPPs. In Ref. [40], the researchers estimated the electrical power output by employing Genetic Algorithm (GA) method for the design
of multilayer perception (MLP) for CCPPs.
Additionally, in the literature, numerous studies [41–47] have been carried to envisage consumption of electrical energy by using
ML intelligence tools, also little studies i.e. [1] carried out related to the calculation of overall electrical power of a CCPP with a heating
system, one steam turbine and three gas turbines. In Ref. [48], authors used an extreme Learning Machine (ELM) as the base regression
model to analyse performance of the power plant in a vigorous atmosphere that can update regression models autonomously to react
with abrupt or gradual environmental changes. In Ref. [49], the authors used Cuckoo Search based ANN to predict output electrical
energy of gas turbine and combined steam mechanisms in order to yield more reliable mechanisms. However, for the first-time deep
learning model based on sequential and functional API neural network modelling is carried out. For the comparison, ANN modelling
based on sequential and functional API is performed. A mathematical model is also developed apart from the soft computing method.
The work adopted for forecasting of CCPP data is started with the description of the CCPP system in section 2. Section 3 discusses the
ANN and DNN method adopted for CCPP modelling. The mathematical modelling, data visualization, ANN and DNN modelling results
are in detail provided in section 4. Conclusions are provided at the end in section 5.
2. CCPP system
A combined cycle power plant (CCPP) consists of steam turbines (ST), heat recovery steam generators (HTSG) and gas turbines
(GT). In CCPP, the ST and electricity generated by gas is combined in lone cycle, and is relocated from one turbine to another [18]. A
GT in a combined cycle system not only produce electrical power (EP) but also produces equally hot gasses. Directing these gases
C.A. Saleel](https://image.slidesharecdn.com/1-s2-240723001757-a9dcae83/85/Total-enegy-forecasting-using-deep-learning-2-320.jpg)
![Case Studies in Thermal Engineering 28 (2021) 101693
3
through a liquid cooled heat exchanger that generates steam, this can be revolved into EP with a coupled generator and ST. Therefore,
a GT generator produces electricity and leftover heat of the exhaust gases is employed to generate steam and additionally produces
electricity through a ST. All around the world, the similar kind of power plants are fitted in increasing numbers where the more
substantial quantities of natural gas are available [19]. For this study the set of data’s are taken from CCPP-1, which is considered with
a small producing capacity of 480 MW, made up of one 160 MW ABB ST, 2 dual pressure heat recovery steam generators (HRSG) and
two 160 MW ABB 13E2 GTs are illustrated in Fig. 1. The load on GT is very sensitive to the atmospheric conditions; essentially relative
humidity (RH), atmospheric pressure (AP) and ambient temperature (AT). On the other hand, the load on ST is very delicate to the
steam exhaust pressure or vacuum. In this study, the factors of both ST and gasses are correlated with exhaust steam pressure and
ambient conditions, are employed as I/P variables as data set. The generation of EP by both STs and gas is employed as a key variable in
the dataset.
All the key variable and I/P variables are defined as below related to hourly average data collected from the measurement sensor
points are denoted in Fig. 1.
1) Ambient Temperature (AT): This I/P variable is restrained in Celsius in degrees as it changes among 1.81 ◦
C and 37.11 ◦
C.
2) Relative Humidity (RH): This I/P variable is restrained as percentage from 25.56% to 100.16%.
3) Vacuum (Exhaust Pressure of Steam, V): This I/P variable is restrained in cm Hg with the variation of 25.36 cm Hg to 81.56 cm Hg.
4) Atmospheric Pressure (AP): This I/P variable is restrained in units of minibar (mbar) with the variation of 992.89 mbar–1033.30
mbar.
5) Full Load EP output (PE): This variable is used as a key variable in the dataset. It is calculated in MW with the variation of 420.26
ME to 495.76 MW.
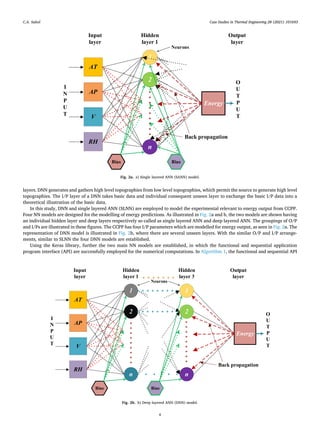
3. Modelling of ANN and DNN
A Neural Network (NN) is a numerical tool that creates calculations built on data from the past. An ANN comprises of various inputs
(I/P) sources that yield inputs built on earlier described data. Then and most importantly, the unseen layers use backpropagations
(BPs) to make the most of neuron’s loads to improve the NNs training. Finally, the output (O/P) layers which are calculated based on
the unseen layer and I/P information. A multi-layered network (MLN) in ANN is known as the backpropagation (BP) NN i.e., most
frequently used. MLN is the utmost common and basic method employed for controlled NNs training by changing and altering the non-
linear correlation between O/P and I/P BP works. In common, the testing and training are two stages of the BP network. In the process
of training, the network is provided with essential classifications and I/Ps. For example, the I/P could be a programmed image of a face
and a program that relates to the individual name that explain the O/P. The Deep Learning (DL) NNs are the key example of a multi-
output or single regression problem algorithm. The various DL archives are available readily to describe and calculate NN models for
multi-O/P regression tasks. DNN is a network built on ANN approach comprising of a group of unseen layers among the O/P and I/P
Fig. 1. Layout of CCPP [18].
C.A. Saleel](https://image.slidesharecdn.com/1-s2-240723001757-a9dcae83/85/Total-enegy-forecasting-using-deep-learning-3-320.jpg)


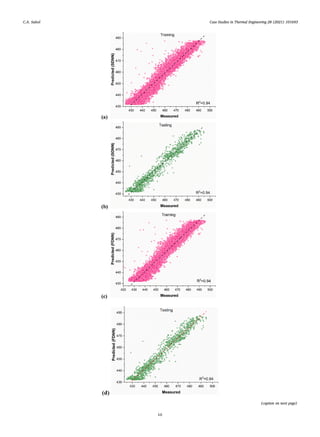
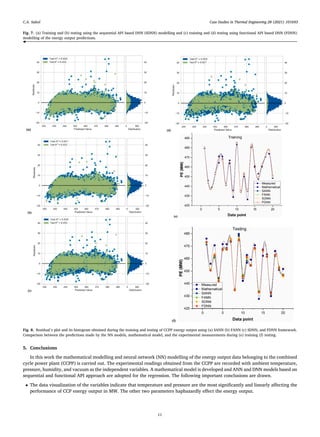
![Case Studies in Thermal Engineering 28 (2021) 101693
12
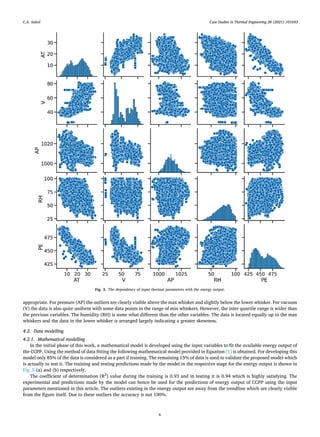
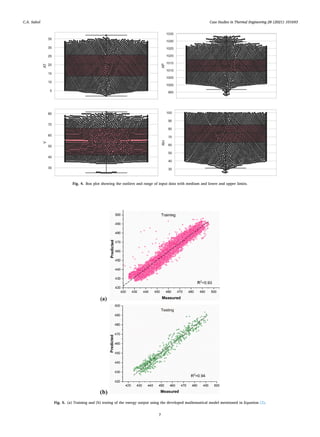
• The box plot variations indicate that the outliers exist in pressure and humidity parameters while in the temperature and vacuum
the variables are in the min and max whisker and interquartile range.
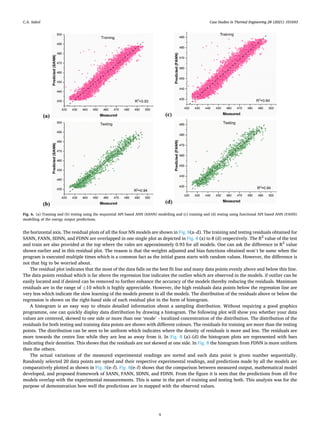
• The mathematical model developed is accurate to predict the energy output of the power plant. Hence this model can be used for
forecasting and when this model is compared with the NN models, the accuracy is similar.
• The four NN models of ANN and DNN developed are in the same range of accuracy and are successfully trained and tested with a
split up of 80% and 20% data.
• The residual plot for al the NN models proposed indicated that the distribution of error is thought in the same range. This is also
confirmed by the sample distribution using histogram.
The work can be extended to apply various machine learning models like support vector machines, gradient boosting algorithms,
ensemble techniques and many more. The mathematical model developed will help in obtaining the optimization of CCPP energy
output. In this regard several latest algorithms available can be easily chosen. Correlation matrix indicating the dependency and
relationship between the factors can also be analysed in future.
Authorship contributions
Category 1
Conception and design of study: C Ahamed Saleel.
Acquisition of data: C Ahamed Saleel.
Analysis and/or interpretation of data: C Ahamed Saleel.
Category 2
Drafting the manuscript: C Ahamed Saleel.
Revising the manuscript critically for important intellectual content: C Ahamed Saleel.
Category 3
Approval of the version of the manuscript to be published (the names of all authors must be listed): C Ahamed Saleel.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to
influence the work reported in this paper.
Acknowledgments
The author extends his appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this
work through Research Group Program under Grant No: RGP 2/105/41.
References
[1] U. Kesgin, H. Heperkan, Simulation of thermodynamic systems using soft computing techniques, Int. J. Energy Res. 29 (2005) 581–611.
[2] A. Samani, Combined cycle power plant with indirect dry cooling tower forecasting using artificial neural network, Decis. Sci. Lett. 7 (2) (2018) 131–142.
[3] P.R. Norvig, S.A. Intelligence, A modern approach, Manuf. Eng. 74 (1995) 111–113.
[4] E. Rich, K. Knight, Artificial Intelligence, McGraw-Hill, New York, 1991.
[5] H.A. Güvenir, Regression on feature projections, Knowl. -Based Syst. 13 (2000) 207–214.
[6] M.T. Hagan, H.B. Demuth, M.H. Beale, Orlando De Jesus. Neural Netw. Des, second ed., Cengage Learn, 2014.
[7] A. Dehghani Samani, Combined cycle power plant with indirect dry cooling tower forecasting using artificial neural network, Decis. Sci. Lett. 7 (2018) 131–142.
[8] H. Kaya, P. Tüfekci, F.S. Gürgen, Local and global learning methods for predicting power of a combined gas & steam turbine, in: International Conference on
Emerging Trends in Computer and Electronics Engineering (ICETCEE’2012), 2012. Dubai, March 24–25.
[9] M. Fast, M. Assadi, S. Deb, Development and multi-utility of an ANN model for an industrial gas turbine, Appl. Energy 86 (1) (2009) 9–17.
[10] D. Jahed Armaghani, M.F. Mohd Amin, S. Yagiz, R.S. Faradonbeh, R.A. Abdullah, Prediction of the uniaxial compressive strength of sandstone using various
modeling techniques, Int. J. Rock Mech. Min. Sci. 85 (2016) 174–186.
[11] H. Moayedi, D. Jahed Armaghani, Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil, Eng. Comput. 34
(2018) 347–356.
[12] A. Afzal, J.K. Bhutto, A. Alrobaian, A.R. Kaladgi, S.A. Khan, Modelling and computational experiment to obtain optimized neural network for battery thermal
management data, Energies 14 (2021) 7370, https://doi.org/10.3390/en14217370.
[13] A. Afzal, S. Alshahrani, A. Alrobaian, A. Buradi, S.A. Khan, Power plant energy predictions based on thermal factors using ridge and support vector regressor
algorithms, Energies 14 (2021) 7254, https://doi.org/10.3390/en14217254.
[14] S. Tamilselvi, S. Gunasundari, N. Karuppiah, A. Razak Rk, S. Madhusudan, V.M. Nagarajan, T. Sathish, M.Z.M. Shamim, C.A. Saleel, A. Afzal, A review on
battery modelling techniques, Sustain. Times 13 (2021) 1–26, https://doi.org/10.3390/su131810042.
[15] A. Chandrashekar, B.V. Chaluvaraju, A. Afzal, D.A. Vinnik, A.R. Kaladgi, S. Alamri, A.S. C, V. Tirth, Mechanical and corrosion studies of friction stir welded nano
Al2O3 reinforced Al-Mg matrix composites: RSM-ANN modelling approach, Symmetry (Basel). 13 (2021) 537, https://doi.org/10.3390/sym13040537.
[16] R. Pinto, A. Afzal, L. D’Souza, Z. Ansari, A.D. Mohammed Samee, Computational fluid dynamics in turbomachinery: a review of state of the art, Arch. Comput.
Methods Eng. 24 (2017) 467–479, https://doi.org/10.1007/s1183.
[17] A. Afzal, Z. Ansari, A. Faizabadi, M. Ramis, Parallelization strategies for computational fluid dynamics software: state of the art review, Arch. Comput. Methods
Eng. 24 (2017) 337–363, https://doi.org/10.1007/s11831-016-9165-4.
[18] C. Wan, Z. Xu, P. Pinson, Z.Y. Dong, K.P. Wong, Optimal prediction intervals of wind power generation, IEEE Trans. Power Syst. 29 (2014) 1166–1174.
[19] F. Bizzarri, M. Bongiorno, A. Brambilla, G. Gruosso, G.S. Gajani, Model of photovoltaic power plants for performance analysis and production forecast, IEEE
Transact. Sustain. Energy 4 (2013) 278–285.
C.A. Saleel](https://image.slidesharecdn.com/1-s2-240723001757-a9dcae83/85/Total-enegy-forecasting-using-deep-learning-12-320.jpg)
![Case Studies in Thermal Engineering 28 (2021) 101693
13
[20] A. Afzal, K.M.Y. Navid, R. Saidur, R.K.A. Razak, R. Subbiah, Back propagation modeling of shear stress and viscosity of aqueous Ionic - MXene nanofluids,
J. Therm. Anal. Calorim. (2021), https://doi.org/10.1007/s10973-021-10743-0.
[21] I. Mokashi, A. Afzal, S.A. Khan, N.A. Abdullah, M.H. Bin Azami, R.D. Jilte, O.D. Samuel, Nusselt number analysis from a battery pack cooled by different fluids
and multiple back-propagation modelling using feed-forward networks, Int. J. Therm. Sci. (2021) 106738, https://doi.org/10.1016/j.ijthermalsci.2020.106738.
[22] A. Afzal, A. Aabid, A. Khan, S. Afghan, U. Rajak, T. Nath, R. Kumar, Response surface analysis , clustering , and random forest regression of pressure in suddenly
expanded high-speed aerodynamic flows, Aero. Sci. Technol. 107 (2020) 106318, https://doi.org/10.1016/j.ast.2020.106318.
[23] A. Afzal, S.A. Khan, T. Islam, R.D. Jilte, A. Khan, M.E.M. Soudagar, Investigation and back-propagation modeling of base pressure at sonic and supersonic Mach
numbers, Phys. Fluids 32 (2020), 096109, https://doi.org/10.1063/5.0022015.
[24] A. Afzal, C.A. Saleel, I.A. Badruddin, T.M.Y. Khan, S. Kamangar, Z. Mallick, O.D. Samuel, M.E.M. Soudagar, Human thermal comfort in passenger vehicles using
an organic phase change material– an experimental investigation, neural network modelling, and optimization, Build. Environ. 180 (2020) 107012, https://doi.
org/10.1016/j.buildenv.2020.107012.
[25] A. Razak, A. Afzal, A.M. Manokar, D. Thakur, U. Agbulut, S. Alshahrani, A.S. C, R. Subbiah, Integrated Taguchi-GRA-RSM optimization and ANN modelling of
thermal performance of zinc oxide nanofluids in an automobile radiator, Case Stud. Therm. Eng. 26 (2021) 101068, https://doi.org/10.1016/j.
csite.2021.101068.
[26] P. Tüfekci, Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods, Int. J. Electr.
Power Energy Syst. 60 (2014) 126–140.
[27] L.X. Niu, X.J. Liu, Multivariable generalized predictive scheme for gas turbine control in combined cycle power plant, IEEE Conf. Cybern. Intellig. Syst. (2008)
791–796, 21-24 September 2008.
[28] M. Rahnama, H. Ghorbani, A. Montazeri, Nonlinear identification of a gas turbine system in transient operation mode using neural network, in: 4th Conference
on Thermal Power Plants (CTPP), IEEE Xplore, 2012.
[29] M.H. Refan, S.H. Taghavi, A. Afshar, Identification of heavy duty gas turbine startup mode by neural networks, in: 4th Conference on Thermal Power Plants
(CTPP), IEEE Xplore, 2012.
[30] Ivan Lorencin, Zlatan Car, Kudláček Jan, Vedran Mrzljak, Nikola Anđelić, Sebastijan Blažević, Estimation of combined cycle power plant power output using
multilayer perceptron variations, in: 10th International Technical Conference-Technological Forum, 2019, pp. 94–98.
[31] Ali Alperen Islikaye, Aydin Cetin, Performance of ML methods in estimating net energy produced in a combined cycle power plant, in: 2018 6th International
Istanbul Smart Grids and Cities Congress and Fair (ICSG), IEEE, 2018, pp. 217–220.
[32] M. Yari, M.A. Shoorehdeli, V94.2 gas turbine identification using neural network, in: First RSI/ISM International Conference on Robotics and Mechatronics
(ICRoM), IEEE Xplore, 2013.
[33] A. Kumar, A. Srivastava, A. Banerjee, A. Goel, Performance based anomaly detection analysis of a gas turbine engine by artificial neural network approach, in:
Procee. Annual Conference of the Prognostics and Health Management Society, 2012.
[34] S.S. Tayarani-Bathaie, Z.N. Sadough Vanini, K. Khorasan, Dynamic neural network-based fault diagnosis of gas turbine engines, Neurocomputing 125 (11)
(2014) 153–165.
[35] M. Rashid, K. Kamal, T. Zafar, Z. Sheikh, A. Shah, S. Mathavan, Energy prediction of a combined cycle power plant using a particle swarm optimization trained
feedforward neural network, in: 2015 International Conference on Mechanical Engineering, Automation and Control Systems (MEACS), IEEE, 2015, pp. 1–5.
[36] Elkhawad Ali Elfaki, Hassan Ahmed, Ahmed, Prediction of electrical output power of combined cycle power plant using regression ANN model, J. Power Energy
Eng. 6 (12) (2018) 17.
[37] Bayram Akdemir, Prediction of hourly generated electric power using artificial neural network for combined cycle power plant, Int. J. Electr. Energy 4 (2)
(2016) 91–95.
[38] Md Hassanul Karim Roni, Muhammad Abdul Goffar Khan, An artificial neural network based predictive approach for analyzing environmental impact on
combined cycle power plant generation, in: 2017 2nd International Conference on Electrical & Electronic Engineering (ICEEE), IEEE, 2017, pp. 1–4.
[39] K. Uma, M. Swetha, M. Manisha, S. Revathi, A. Kannan, IOT based environment condition monitoring system, Indian J. Sci. Technol. 10 (2017).
[40] Ivan Lorencin, Nikola Anđelić, Vedran Mrzljak, Zlatan Car, Genetic algorithm approach to design of multi-layer perceptron for combined cycle power plant
electrical power output estimation, Energies 12 (22) (2019) 4352.
[41] G.K.F. Tso, K.K.W. Yau, Predicting electricity energy consumption: a comparison of regression analysis, decision tree and neural networks, Energy 32 (9) (2007)
1761–1768.
[42] A. Azadeh, M. Saberi, O. Seraj, An integrated fuzzy regression algorithm for energy consumption estimation with non-stationary data: a case study of Iran,
Energy 35 (6) (2010) 2351–2366.
[43] L. Ekonomou, Greek long-term energy consumption prediction using artificial neural networks, Energy 35 (2) (2010) 512–517.
[44] J. Che, J. Wang, G. Wang, An adaptive fuzzy combination model based on self-organizing map and support vector regression for electric load forecasting, Energy
37 (1) (2012) 657–664.
[45] K. Kavaklioglu, Modeling and prediction of Turkey’s electricity consumption using support vector regression, Appl. Energy 88 (2011) 368–375.
[46] P.C.M. Leung, E.W.M. Lee, Estimation of electrical power consumption in subway station design by intelligent approach, Appl. Energy 101 (2013) 634–643.
[47] M.R. Alrashidi, K.M. El-Naggar, Long term electric load forecasting based on particle swarm optimization, Appl. Energy 87 (2010) 320–326.
[48] Rui Xu, WeiZhong Yan, Continuous modeling of power plant performance with regularized extreme learning machine, in: 2019 International Joint Conference
on Neural Networks (IJCNN), IEEE, 2019, pp. 1–8.
[49] Sankhadeep Chatterjee, Nilanjan Dey, Amira S. Ashour, Cornelia Victoria Anghel Drugarin, Electrical energy output prediction using cuckoo search based
artificial neural network, in: Smart Trends in Systems, Security and Sustainability, Springer, Singapore, 2018, pp. 277–285.
C.A. Saleel](https://image.slidesharecdn.com/1-s2-240723001757-a9dcae83/85/Total-enegy-forecasting-using-deep-learning-13-320.jpg)