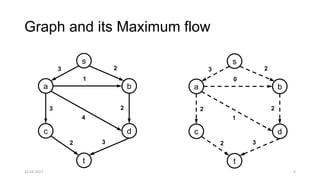
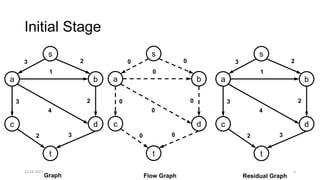
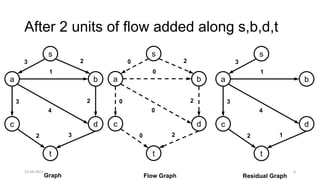
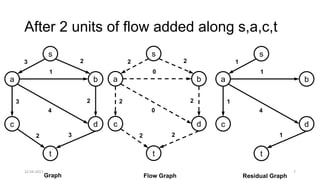
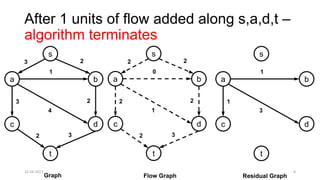
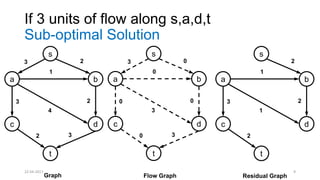
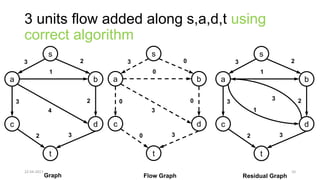
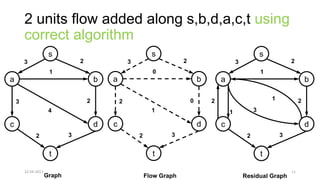
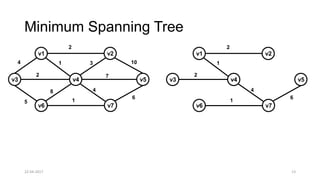
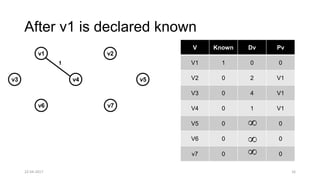
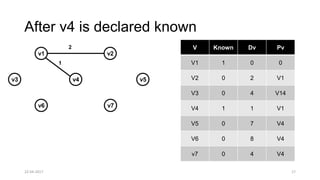
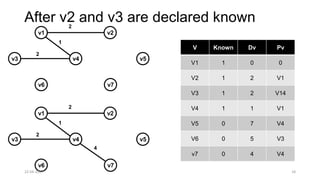
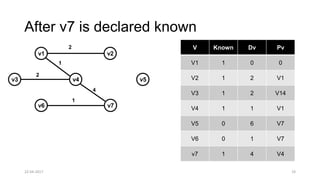
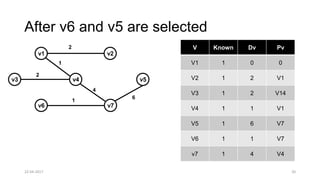
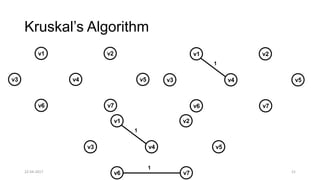
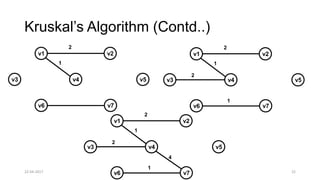
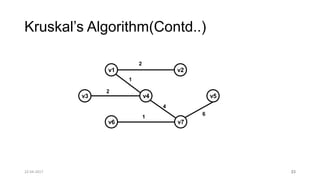
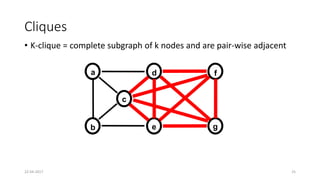
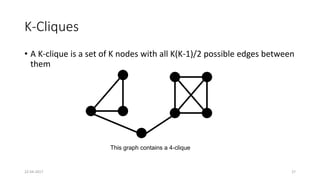
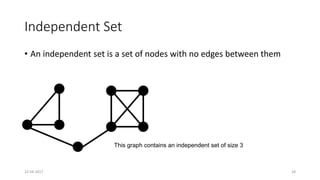
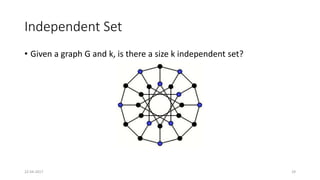
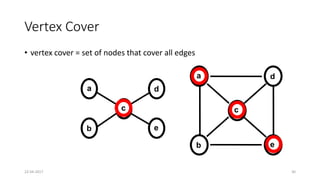
The document discusses theoretical foundations of computer science with a focus on graph algorithms, including network flow problems and spanning trees. It introduces algorithms such as Prim's and Kruskal's for finding minimum spanning trees and highlights applications in real-time scenarios like traffic flow and GPS navigation. It also covers NP-complete problems in graphs, such as k-clique and vertex cover, illustrating their complexities and applications in various fields.

1. Theoretical Foundations of
Computer Science
(Graphs)
J.J. ADRI JOVIN
Assistant Professor (Sr. Gr.)/IT
22-04-2017 1

2. Network Flow Problems
22-04-2017 2

3. Real-time Applications
• Water Flow through a pipe
• Amount of traffic that can flow on a street between two
intersections
22-04-2017 3

4. Graph and its Maximum flow
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
3 2
0
2 2
1
2 3
22-04-2017 4

5. Initial Stage
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
0 0
0
0 0
0
0 0
s
t
a b
c d
3 2
1
3 2
4
2 3
Graph Flow Graph Residual Graph
22-04-2017 5

6. After 2 units of flow added along s,b,d,t
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
0 2
0
0 2
0
0 2
s
t
a b
c d
3
1
3
4
2 1
Graph Flow Graph Residual Graph
22-04-2017 6

7. After 2 units of flow added along s,a,c,t
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
2 2
0
2 2
0
2 2
s
t
a b
c d
1
1
1
4
1
Graph Flow Graph Residual Graph
22-04-2017 7

8. After 1 units of flow added along s,a,d,t –
algorithm terminates
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
2 2
0
2 2
1
2 3
s
t
a b
c d
1
1
3
Graph Flow Graph Residual Graph
22-04-2017 8

9. If 3 units of flow along s,a,d,t
Sub-optimal Solution
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
3 0
0
0 0
3
0 3
s
t
a b
c d
2
1
3 2
1
2
Graph Flow Graph Residual Graph
22-04-2017 9

10. 3 units flow added along s,a,d,t using
correct algorithm
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
3 0
0
0 0
3
0 3
s
t
a b
c d
3 2
1
3 2
2 3
Graph Flow Graph Residual Graph
1
3
22-04-2017 10

11. 2 units flow added along s,b,d,a,c,t using
correct algorithm
s
t
a b
c d
3 2
1
3 2
4
2 3
s
t
a b
c d
3 2
0
2 0
1
2 3
s
t
a b
c d
3 2
1
2
2 3
Graph Flow Graph Residual Graph
3
1
1
2
22-04-2017 11

12. Spanning Trees
• Prim’s Algorithm
• Kruskal’s Algorithm
Real-time Applications
• Wiring
• GPS Navigation
22-04-2017 12

13. v1 v2
v6 v7
v5v4v3
2
1
6
4
1
2
v1 v2
v6 v7
v5v4v3
2
1 3 10
6
7
4
1
2
4
5
8
Minimum Spanning Tree
22-04-2017 13

14. Prim’s Algorithm
22-04-2017 14

15. v1 v2
v6 v7
v5v4v3
V Known Dv Pv
V1 0 0 0
V2 0 0
V3 0 0
V4 0 0
V5 0 0
V6 0 0
v7 0 0







Initial Configuration
22-04-2017 15

16. v1 v2
v6 v7
v5v4v3
1
V Known Dv Pv
V1 1 0 0
V2 0 2 V1
V3 0 4 V1
V4 0 1 V1
V5 0 0
V6 0 0
v7 0 0



After v1 is declared known
22-04-2017 16

17. v1 v2
v6 v7
v5v4v3
2
1
V Known Dv Pv
V1 1 0 0
V2 0 2 V1
V3 0 4 V14
V4 1 1 V1
V5 0 7 V4
V6 0 8 V4
v7 0 4 V4
After v4 is declared known
22-04-2017 17

18. v1 v2
v6 v7
v5v4v3
2
1
2
V Known Dv Pv
V1 1 0 0
V2 1 2 V1
V3 1 2 V14
V4 1 1 V1
V5 0 7 V4
V6 0 5 V3
v7 0 4 V4
v1 v2
v6 v7
v5v4v3
2
1
2
4
After v2 and v3 are declared known
22-04-2017 18

19. v1 v2
v6 v7
v5v4v3
2
1
4
1
2
V Known Dv Pv
V1 1 0 0
V2 1 2 V1
V3 1 2 V14
V4 1 1 V1
V5 0 6 V7
V6 0 1 V7
v7 1 4 V4
After v7 is declared known
22-04-2017 19

20. v1 v2
v6 v7
v5v4v3
2
1
6
4
1
2
V Known Dv Pv
V1 1 0 0
V2 1 2 V1
V3 1 2 V14
V4 1 1 V1
V5 1 6 V7
V6 1 1 V7
v7 1 4 V4
After v6 and v5 are selected
22-04-2017 20

21. v1 v2
v6 v7
v5v4v3
Kruskal’s Algorithm
v1 v2
v6 v7
v5v4v3
1
v1 v2
v6 v7
v5v4v3
1
1
22-04-2017 21

22. v1 v2
v6 v7
v5v4v3
2
1
Kruskal’s Algorithm (Contd..)
v1 v2
v6 v7
v5v4v3
2
1
1
2
v1 v2
v6 v7
v5v4v3
2
1
4
1
2
22-04-2017 22

23. Kruskal’s Algorithm(Contd..)
v1 v2
v6 v7
v5v4v3
2
1
6
4
1
2
22-04-2017 23

24. NP-Complete Problems in Graphs
• K-Clique
• Vertex Cover
• Independent Set
22-04-2017 24

25. Cliques
• K-clique = complete subgraph of k nodes and are pair-wise adjacent
22-04-2017 25
b
a
e
c
d f
g

26. Real-time Applications
• Social Networks
• Computing Protein Similarity
• Finding Error Correcting Codes
22-04-2017 26

27. K-Cliques
• A K-clique is a set of K nodes with all K(K-1)/2 possible edges between
them
22-04-2017 27
This graph contains a 4-clique

28. Independent Set
• An independent set is a set of nodes with no edges between them
22-04-2017 28
This graph contains an independent set of size 3

29. Independent Set
• Given a graph G and k, is there a size k independent set?
22-04-2017 29

30. Vertex Cover
• vertex cover = set of nodes that cover all edges
22-04-2017 30
b
a
e
c
d
b
a
e
c
d

31. Vertex Cover is NP Complete
• Given a Graph G(V,E), decide if there is k vertex such that every edge
is covered by one of them?
22-04-2017 31

32. References
• “Data Structures and Algorithms”, 2nd Ed., Mark Allen Weiss
• “Data Structures”, Seymour Lipschutz
• “Data Structures with C++”, John R. Hubbard
• “Formal Languages, Automata, and Computation (FLAC)”,
http://www.cs.cmu.edu/~emc/flac09/lectures/ by Edmund M.
Clarke
22-04-2017 32