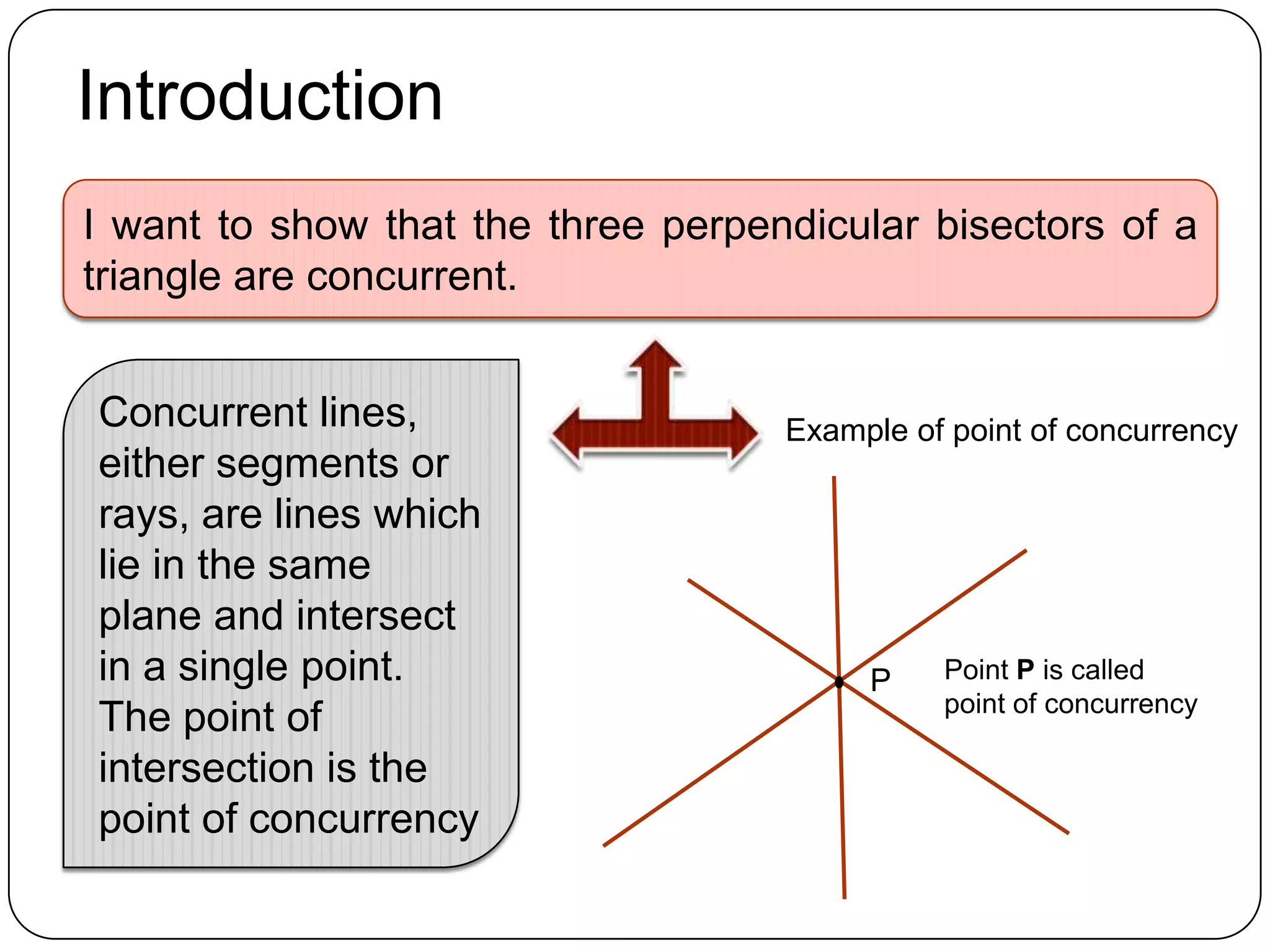
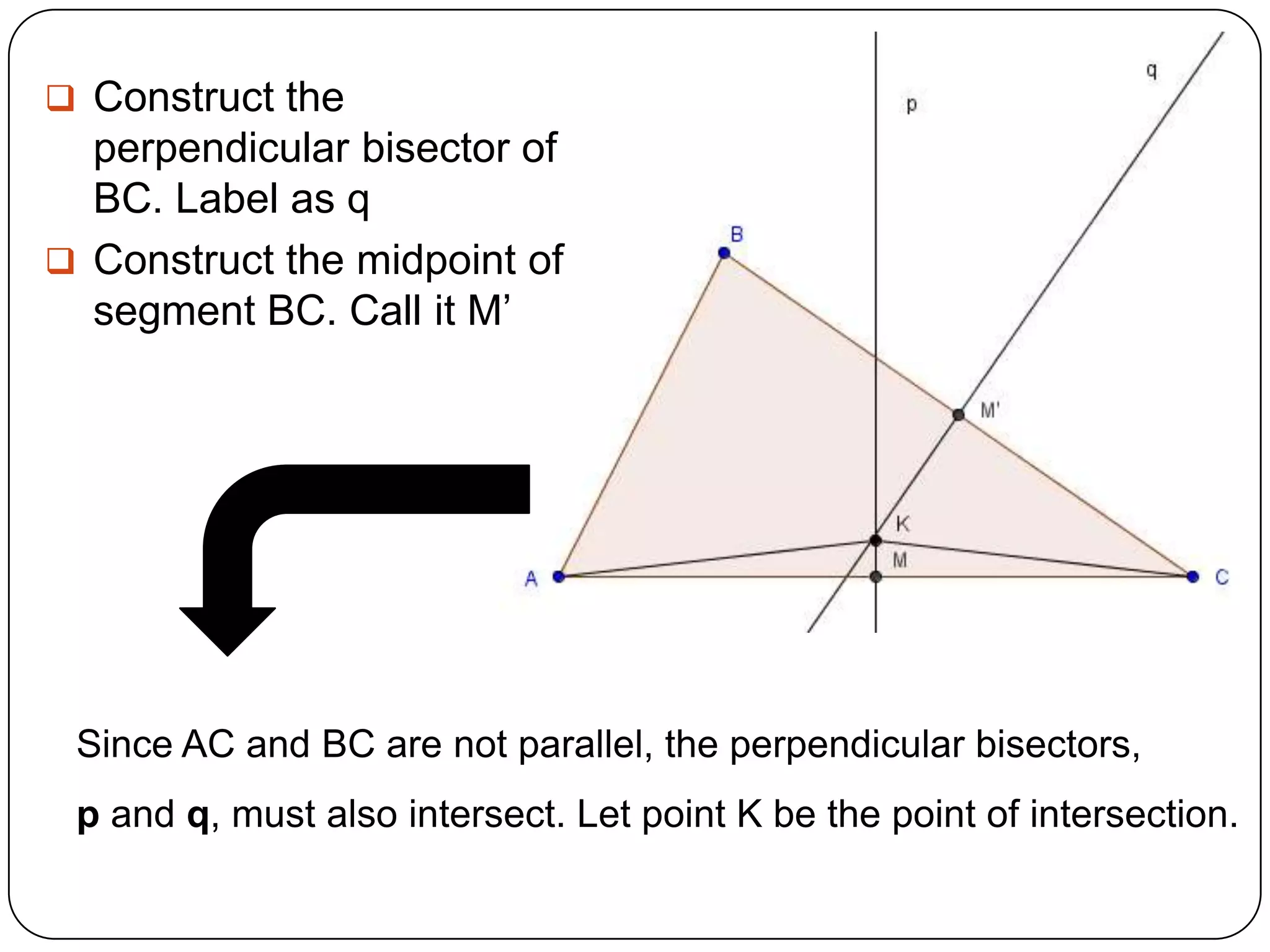
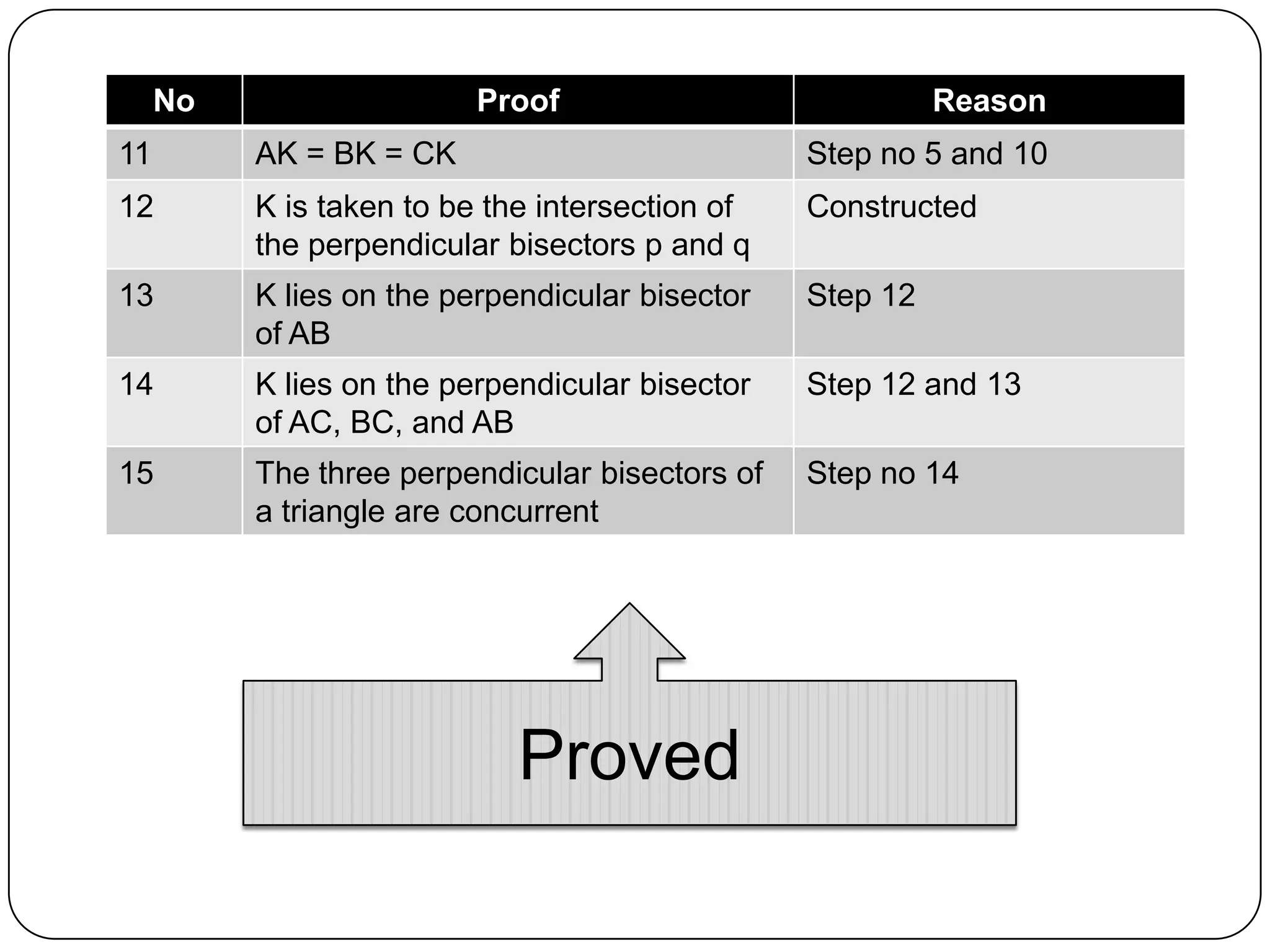
The three perpendicular bisectors of a triangle are concurrent. This is proved by showing that the perpendicular bisector of one side of a triangle passes through the midpoint of that side. It is then shown that the other two perpendicular bisectors intersect at the same point due to angle and side properties of similar triangles. This common point of intersection is the point of concurrency where all three perpendicular bisectors meet.

1. Created by Laurado Rindira Sabatini
Three Perpendicular Bisector
of A Triangle are Concurrent

2. Introduction
I want to show that the three perpendicular bisectors of a
triangle are concurrent.
Concurrent lines,
either segments or
rays, are lines which
lie in the same
plane and intersect
in a single point.
The point of
intersection is the
point of concurrency
Example of point of concurrency
P
Point P is called
point of concurrency

3. Proof
 Given ∆ ABC
 Construct the
perpendicular bisector
of segment AC. Label
as p
 Construct the midpoint
of segment AC. Call M

4.  Construct any point K
on the perpendicular
bisector p
 Construct segment AK
and segment KC
No
Proof
Reason
1
AM = CM
Definition of midpoint
2
KM = KM
Reflective property
3
m⦟ AMK = m ⦟ CMK Right angles
4
∆ AMK ≈ ∆ CMK
Side – Angled - Side
5
AK = CK
Step no 4

5.  Construct the
perpendicular bisector of
BC. Label as q
 Construct the midpoint of
segment BC. Call it M’
Since AC and BC are not parallel, the perpendicular bisectors,
p and q, must also intersect. Let point K be the point of intersection.

6.  Construct point K as
the point of
intersection p and q
 Construct segment BK
No
Proof
Reason
6
BM’ = CM’
Definition of midpoint
7
KM’ = KM’
Reflective property
8
m⦟ BM’K = m ⦟
CM’K
Right angles
9
∆ BM’K ≈ ∆ CM’K
Side – Angled - Side
10
BK = CK
Step no 4
Continued

7. No
Proof
Reason
11
AK = BK = CK
Step no 5 and 10
12
K is taken to be the intersection of
the perpendicular bisectors p and q
Constructed
13
K lies on the perpendicular bisector
of AB
Step 12
14
K lies on the perpendicular bisector
of AC, BC, and AB
Step 12 and 13
15
The three perpendicular bisectors of
a triangle are concurrent
Step no 14
Proved

8. Thanks for Your Attention!!!
Please visit:
lauradorindira.wordpress.com